Article contents
Truth definitions in finite models
Published online by Cambridge University Press: 12 March 2014
Abstract
The paper discusses the notion of finite model truth definitions (or FM-truth definitions), introduced by M. Mostowski as a finite model analogue of Tarski's classical notion of truth definition.
We compare FM-truth definitions with Vardi's concept of the combined complexity of logics, noting an important difference: the difficulty of defining FM-truth for a logic 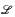 does not depend on the syntax of
does not depend on the syntax of 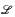 , as long as it is decidable. It follows that for a natural
, as long as it is decidable. It follows that for a natural 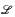 there exist FM-truth definitions whose evaluation is much easier than the combined complexly of
there exist FM-truth definitions whose evaluation is much easier than the combined complexly of 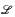 would suggest.
would suggest.
We apply the general theory to give a complexity-theoretical characterization of the logics for which the 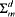 classes (prenex classes of higher order logics) define FM-truth. For any d ≥ 2, m ≥ 1 we construct a family
classes (prenex classes of higher order logics) define FM-truth. For any d ≥ 2, m ≥ 1 we construct a family 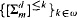 of syntactically defined fragments of
of syntactically defined fragments of 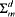 which satisfy this characterization. We also use the
which satisfy this characterization. We also use the 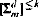 classes to give a refinement of known results on the complexity classes captured by
classes to give a refinement of known results on the complexity classes captured by 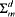 .
.
We close with a few simple corollaries, one of which gives a sufficient condition for the existence, given a vocabulary σ, of a fixed number k such that model checking for all first order sentences over σ can be done in deterministic time nk.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2004
References
REFERENCES
- 8
- Cited by




