Article contents
Stability and posets
Published online by Cambridge University Press: 12 March 2014
Abstract
Hirschfeldt and Shore have introduced a notion of stability for infinite posets. We define an arguably more natural notion called weak stability, and we study the existence of infinite computable or low chains or antichains, and of infinite 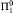 chains and antichains, in infinite computable stable and weakly stable posets. For example, we extend a result of Hirschfeldt and Shore to show that every infinite computable weakly stable poset contains either an infinite low chain or an infinite computable antichain. Our hardest result is that there is an infinite computable weakly stable poset with no infinite
chains and antichains, in infinite computable stable and weakly stable posets. For example, we extend a result of Hirschfeldt and Shore to show that every infinite computable weakly stable poset contains either an infinite low chain or an infinite computable antichain. Our hardest result is that there is an infinite computable weakly stable poset with no infinite 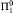 chains or antichains. On the other hand, it is easily seen that every infinite computable stable poset contains an infinite computable chain or an infinite
chains or antichains. On the other hand, it is easily seen that every infinite computable stable poset contains an infinite computable chain or an infinite 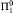 antichain. In Reverse Mathematics, we show that SCAC, the principle that every infinite stable poset contains an infinite chain or antichain, is equivalent over RCA0 to WSAC, the corresponding principle for weakly stable posets.
antichain. In Reverse Mathematics, we show that SCAC, the principle that every infinite stable poset contains an infinite chain or antichain, is equivalent over RCA0 to WSAC, the corresponding principle for weakly stable posets.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2009
References
REFERENCES
- 3
- Cited by




