Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-24T18:29:35.367Z Has data issue: false hasContentIssue false
  • English
  • Français

Generic Σ31 absoluteness

Published online by Cambridge University Press:  12 March 2014

Sy D. Friedman
Sy D. Friedman*
Affiliation:
Institute for Logic, University of Vienna, Waehringer Strasse 25, A-1090 Vienna, Austria Mathematics Department, MIT, Cambridge. Massachusetts 02139, USA, E-mail: sdf@logic.univie.ac.at
Get access Rights & Permissions [Opens in a new window]

Extract

In this article we study the strength of 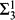absoluteness (with real parameters) in various types of generic extensions, correcting and improving some results from [3]. (In particular, see Theorem 3 below.) We shall also make some comments relating this work to the bounded forcing axioms BMM, BPFA and BSPFA.

The statement “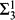 absoluteness holds for ccc forcing” means that if a 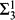formula with real parameters has a solution in a ccc set-forcing extension of the universe V, then it already has a solution in V. The analogous definition applies when ccc is replaced by other set-forcing notions, or by class-forcing.

Theorem 1. [1] 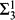absoluteness for ccc has no strength; i.e., if ZFC is consistent then so is ZFC + 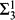absoluteness for ccc.

The following results concerning (arbitrary) set-forcing and class-forcing can be found in [3].

Theorem 2 (Feng-Magidor-Woodin). (a) 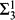absoluteness for arbitrary set-forcing is equiconsistent with the existence of a reflecting cardinal, i.e., a regular cardinal κ such that H(κ) is ∑2-elementary in V.

(b) 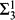absoluteness for class-forcing is inconsistent.

We consider next the following set-forcing notions, which lie strictly between ccc and arbitrary set-forcing: proper, semiproper, stationary-preserving and ω1-preserving. We refer the reader to [8] for the definitions of these forcing notions.

Using a variant of an argument due to Goldstern-Shelah (see [6]), we show the following. This result corrects Theorem 2 of [3] (whose proof only shows that if 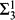absoluteness holds in a certain proper forcing extension, then in L either ω1 is Mahlo or ω2 is inaccessible).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 69 , Issue 1 , March 2004 , pp. 73 - 80
Copyright
Copyright © Association for Symbolic Logic 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bagaria, J., A characterization of Martin's axiom in terms of absoluteness, this Journal, vol. 62 (1997), no. 2, pp. 366–372.Google Scholar
[2]Bagaria, J., Bounded forcing axioms as principles of generic absoluteness, Archive for Mathematical Logic, vol. 39 (2000), no. 6, pp. 393–401.CrossRefGoogle Scholar
[3]Bagaria, J. and Friedman, S., Generic absoluteness, Annals of Pure and Applied Logic, vol. 108 (2001), pp. 3–13.CrossRefGoogle Scholar
[4]Feng, Q., Magidor, M., and Woodin, H., Universally Baire sets of reals, Set theory of the continuum, Mathematical Sciences Research Institute Publications, vol. 26, Springer, New York, 1992, pp. 203–242.Google Scholar
[5]Friedman, S., Fine structure and class forcing, de Gruyter Series in Logic and its Applications, vol. 3, Walter de Gruyter & Co., Berlin, 2000.Google Scholar
[6]Goldstern, M. and Shelah, S., The bounded proper forcing axiom, this Journal, vol. 60 (1995), no. 1, pp. 58–73.Google Scholar
[7]Harrington, L. and Shelah, S., Some exact equiconsistency results in set theory, Notre Dame Journal of Formal Logic, vol. 26 (1985), pp. 178–188.Google Scholar
[8]Jech, T., Set Theory, Springer Monographs in Mathematics, 2002.Google Scholar
[9]Schindler, R., Coding into K by reasonable forcing, Transactions of the American Mathematical Society, vol. 353 (2000), pp. 479–489.CrossRefGoogle Scholar
[10]Schindler, R., BMM is stronger than BSPFA, preprint, 05 2003.Google Scholar
[11]Schindler, R., Forcing axioms and projective sets of reals, to appear, Proceedings of the conference “Foundations of the Formal Sciences III”, Kluwer.Google Scholar
[12]Schrittesser, D., absoluteness in forcing extensions, Diplomarbeit, Universität Wien, to appear.Google Scholar
[13]Shelah, S. and Stanley, L., Coding and reshaping when there are no sharps, Set theory of the continuum, Mathematical Sciences Research Institute Publications, vol. 26, Springer, New York, 1992, pp. 407–416.Google Scholar
[14]Woodin, W. H., The axiom of determinacy, forcing axioms, and the nonstationary ideal, de Gruyter Series in Logic and its Applications, vol. 1, Walter de Gruyter & Co., Berlin, 1999.Google Scholar