Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-25T00:43:09.343Z Has data issue: false hasContentIssue false
  • English
  • Français

Analytic countably splitting families

Published online by Cambridge University Press:  12 March 2014

Otmar Spinas
Otmar Spinas*
Affiliation:
Mathematisches Seminar, Christian-Albrechts-Universität Zu Kiel, Ludewig-Meyn-Straße 4, 24098 Kiel, Germany, E-mail: spinas@math.uni-kiel.de
Get access Rights & Permissions [Opens in a new window]

Abstract

A family A ⊆ 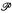(ω) is called countably splitting if for every countable F ⊆ [ω]ω, some element of A splits every member of F. We define a notion of a splitting tree, by means of which we prove that every analytic countably splitting family contains a closed countably splitting family. An application of this notion solves a problem of Blass. On the other hand we show that there exists an Fσ splitting family that does not contain a closed splitting family.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 69 , Issue 1 , March 2004 , pp. 101 - 117
Copyright
Copyright © Association for Symbolic Logic 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Blass, A., Reductions between cardinal characteristics of the continuum, Set theory (Annual Boise extravaganza in set theory conference, 1992–94) (Bartoszyński, T. and Scheepers, M., editors), Contemporary Mathematics, vol. 192, American Mathematical Society, 1996, pp. 31–49.Google Scholar
[2]Blass, A., Combinatorial cardinal characteristics of the continuum. Handbook of Set Theory, to appear.Google Scholar
[3]Brendle, J., Hjorth, G., and Spinas, O., Regularity properties for dominating projective sets. Annals of Pure and Applied Logic, vol. 72 (1995), pp. 291–307.CrossRefGoogle Scholar
[4]Davis, M., Infinite games of perfect information. Annals of Mathematics Studies, vol. 52 (1964), pp. 85–101.Google Scholar
[5]Kechris, A. S., On a notion of smallness for subsets of the Baire space. Transactions of the American Mathematical Society, vol. 229 (1977), pp. 191–207.Google Scholar
[6]Kechris, A. S., Classical descriptive set theory, Springer-Verlag, New York. 1995.CrossRefGoogle Scholar
[7]Kunen, K., Set theory, An introduction to independence proofs, North-Holland Publishing Co.. Amsterdam, 1983.Google Scholar
[8]Kuratowski, K., Topology, vol. 1, Academic Press, 1980.Google Scholar
[9]Martin, D., Borel determinacy. Annals of Mathematics, II, vol. 102 (1975), pp. 363–371.CrossRefGoogle Scholar
[10]Mildenberger, H., Non-constructive Galois-Tukey connections, this Journal, vol. 62 (1997), pp. 1179–1187.Google Scholar
[11]Martin, D., No Borel connections for the unsplitting relations. Mathematical Logic Quarterly, vol. 48 (2002), pp. 517–521.Google Scholar
[12]Raymond, J. Saint, Approximation des sous-ensembles analytiques par l'intérieur, Comptes Rendus de l'Académie des Sciences Paris, Série A, vol. 281 (1975), pp. 85–87.Google Scholar
[13]Spinas, O., Dominating projective sets in the Baire space. Annals of Pure and Applied Logic, vol. 68 (1994). pp. 327–342.Google Scholar
[14]Vojtáš, P., Generalized Galois-Tukey connections between relations on classical objects of real analysis, Set theory of the reals (Judah, H., editor), Israel Mathematical Conference Proceedings, vol. 6, American Mathematical Society, 1993, pp. 619–643.Google Scholar
[15]Yiparaki, O., On some tree partitions, Ph.D. thesis, University of Michigan, 1994.Google Scholar