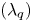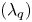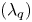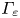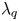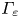1. Introduction
The high-confinement mode (H-mode), characterized by steep pressure gradients at the plasma edge and associated edge localized modes (ELMs), is the operational regime foreseen for future fusion devices (Wagner et al. Reference Wagner1982; Mukhovatov et al. Reference Mukhovatov2003; Shimada et al. Reference Shimada2007). However, type-I ELMs, characterized by a low repetition frequency and localized periodic collapse at the edge with large ELM size, are not expected to be tolerable due to the high heat and particle loads on plasma facing components in large-scale tokamaks, such as ITER (Mukhovatov et al. Reference Mukhovatov2003; Loarte et al. Reference Loarte2007; Shimada et al. Reference Shimada2007) or future DEMOnstration Power Plants (Riccardi et al. Reference Riccardi, Giniatulin, Klimov, Koidan and Loarte2011; Eich et al. Reference Eich, Sieglin, Thornton, Faitsch, Kirk, Herrmann and Suttrop2017). Simultaneous control of large ELMs and divertor heat loads in an H-mode plasma are crucial for steady-state operation of a tokamak fusion reactor. Recently, experiments showed that H-mode plasma regimes with small/grassy ELMs offer a potential solution for core-edge-integration to future tokamak reactors (Viezzer et al. Reference Viezzer2023). In addition, DIII-D and ASDEX Upgrade experiments showed that the heat flux width is broadened with quasi-continuous particle and power exhaust to the divertors, and the peak divertor heat flux is much smaller for small/grassy ELMs (Nazikian et al. Reference Nazikian2018; Xu Reference Xu2020; Faitsch et al. Reference Faitsch, Eich, Harrer, Wolfrum, Brida, David, Griener and Stroth2021).
The exploration of small/grassy ELM regimes compatible with favourable energy confinement has intensively been conducted in many devices. A grassy ELM regime was found in JT-60U, which was compatible with high energy confinement in a carbon wall at a low pedestal collisionality ${\nu ^\ast }\sim 0.29\,-\, 0.72$![]() (Oyama et al. Reference Oyama2007). The grassy ELMs are characterized by a high repetition frequency and localized periodic collapse at the edge with small ELM size. The energy loss due to the grassy ELMs is estimated to be smaller than 1 % of the pedestal stored energy. In NSTX, a small ELM regime (type-V ELM) was observed in discharges with boron wall conditioning at high ${\nu ^\ast }$
(Oyama et al. Reference Oyama2007). The grassy ELMs are characterized by a high repetition frequency and localized periodic collapse at the edge with small ELM size. The energy loss due to the grassy ELMs is estimated to be smaller than 1 % of the pedestal stored energy. In NSTX, a small ELM regime (type-V ELM) was observed in discharges with boron wall conditioning at high ${\nu ^\ast }$![]() (Maingi et al. Reference Maingi2005). EAST observed a grassy ELM regime in a metal wall at high density/collisionality ${\nu ^\ast }$
(Maingi et al. Reference Maingi2005). EAST observed a grassy ELM regime in a metal wall at high density/collisionality ${\nu ^\ast }$![]() (Xu et al. Reference Xu2019a). A wide pedestal with a low pedestal density gradient is an essential condition for access to the grassy ELM regime, in addition to high ${q_{95}}$
(Xu et al. Reference Xu2019a). A wide pedestal with a low pedestal density gradient is an essential condition for access to the grassy ELM regime, in addition to high ${q_{95}}$![]() or high poloidal magnetic field ${B_p}$
or high poloidal magnetic field ${B_p}$![]() (Li et al. Reference Li, Xu, Wang, Lin, Yan and Xu2022a; Xu Reference Xu2022). In AUG, the type-II ELM regime, where high confinement and small ELMs occur simultaneously, was achieved with high SOL density (Stober et al. Reference Stober, Maraschek, Conway, Gruber, Herrmann, Sips, Treutterer, Zohm and Team2001; Wolfrum et al. Reference Wolfrum2011). The quasi-continuous exhaust (QCE) regime was observed at the pedestal foot in the case with high separatrix density by gas fuelling (Harrer et al. Reference Harrer2018, Reference Harrer2022). The power fall-off length in the QCE regime measured with the infrared diagnostic in the divertor is increased by a factor of 4, when compared with the scaling for the inter-ELM power exhaust profile width (Faitsch et al. Reference Faitsch, Eich, Harrer, Wolfrum, Brida, David, Griener and Stroth2021). In JET, a Baseline Small ELM (BSE) regime has been found, where simultaneous access to small ELMs, high confinement and high D–D fusion rate were achieved without core impurity accumulation (Garcia et al. Reference Garcia2022).
(Li et al. Reference Li, Xu, Wang, Lin, Yan and Xu2022a; Xu Reference Xu2022). In AUG, the type-II ELM regime, where high confinement and small ELMs occur simultaneously, was achieved with high SOL density (Stober et al. Reference Stober, Maraschek, Conway, Gruber, Herrmann, Sips, Treutterer, Zohm and Team2001; Wolfrum et al. Reference Wolfrum2011). The quasi-continuous exhaust (QCE) regime was observed at the pedestal foot in the case with high separatrix density by gas fuelling (Harrer et al. Reference Harrer2018, Reference Harrer2022). The power fall-off length in the QCE regime measured with the infrared diagnostic in the divertor is increased by a factor of 4, when compared with the scaling for the inter-ELM power exhaust profile width (Faitsch et al. Reference Faitsch, Eich, Harrer, Wolfrum, Brida, David, Griener and Stroth2021). In JET, a Baseline Small ELM (BSE) regime has been found, where simultaneous access to small ELMs, high confinement and high D–D fusion rate were achieved without core impurity accumulation (Garcia et al. Reference Garcia2022).
To understand the underlying physics of these small/grassy ELM regimes, both theory and simulations are performed for different tokamak devices. Stability analysis for the JT-60U grassy ELM shows that short wavelength (high toroidal mode numbers) ballooning modes can play an important role in the stability of a grassy ELM. Low plasma ellipticity is preferable to realize a grassy ELM plasma, due to destabilization of the ballooning mode (Aiba & Oyama Reference Aiba and Oyama2012). Linear edge stability analysis has shown that the pedestal in the BSE plasmas for JET is not limited by PB modes, indicating that mechanisms, other than ideal MHD, are responsible for the onset of such ELMs (Garcia et al. Reference Garcia2022). The underlying physics for such small ELMs in JET is still not clear and needs further investigation. JOREK simulations for ASDEX Upgrade with high density have successfully reproduced several key observations from the small ELM regime. These simulations suggest that the small ELMs may be driven by resistive peeling-ballooning modes, which exhibit strong localization near the separatrix (Cathey et al. Reference Cathey, Hoelzl, Harrer, Dunne, Huijsmans, Lackner, Pamela, Wolfrum and Günter2022). BOUT++ nonlinear simulations for EAST indicate that small ELM crashes are accompanied by the upward movement of the peeling boundary induced by an initial radially localized collapse in the pedestal, which stops the growth of instabilities (Xu et al. Reference Xu2019a). The linear and nonlinear simulations for a long-pulse, high-${q_{95}}$![]() , high-${B_p}$
, high-${B_p}$![]() grassy ELM shows that the ELM crash is triggered by low-n peeling modes, and fluctuations are generated at the peak pressure gradient position and then radially spread outward into the scrape-off-layer (SOL) (Li et al. Reference Li, Xu, Wang, Yan, Zhang, Qian, Sun and Wang2022b). The divertor heat flux width is ~2 times larger than that estimated by the ITPA multi-machines scaling law, due to strong turbulent transport (Li et al. Reference Li, Xu, Wang, Yan, Zhang, Qian, Sun and Wang2022b). The pedestal density/collisionality and width scans for EAST indicate that small ELMs can be triggered by marginally unstable modes. These modes include low-n peeling modes, high-n ballooning modes, intermediate-n peeling-ballooning modes or a local ballooning instability in the pedestal foot, particularly in the presence of a larger separatrix density gradient (Li et al. Reference Li, Xu, Wang, Lin, Yan and Xu2022a). The size of the ELM, whether small or large, strongly depends on the inward avalanching and turbulence spreading from the linearly unstable zone to the stable zone during the nonlinear saturation phase (Li et al. Reference Li, Xu, Wang, Lin, Yan and Xu2022a). In the small/grassy ELM regime, the SOL turbulent thermal diffusivity increases due to larger turbulent fluxes being ejected from the pedestal into the SOL, resulting in a broadening of the SOL width (Li et al. Reference Li, Xu, Li, Chan and Wang2019; Xu et al. Reference Xu, Li, Li, Chen, Xia, Tang, Zhu and Chan2019b; Li et al. Reference Li, Xu, Hughes, Terry, Sun and Wang2020). Therefore, considering tokamak operational regimes with small ELMs may offer a potential solution to address the challenge of managing large transient heat loads in fusion reactors. However, several kept aspects of the underlying physics in the small ELM regime remain unclear. Questions persist regarding how to control the inward penetration and outward spreading phenomena, and how these processes influence the size of ELMs and the width of the SOL. Further investigation is crucial to understand the impact of turbulence spreading on the evolution of edge profiles and SOL width.
grassy ELM shows that the ELM crash is triggered by low-n peeling modes, and fluctuations are generated at the peak pressure gradient position and then radially spread outward into the scrape-off-layer (SOL) (Li et al. Reference Li, Xu, Wang, Yan, Zhang, Qian, Sun and Wang2022b). The divertor heat flux width is ~2 times larger than that estimated by the ITPA multi-machines scaling law, due to strong turbulent transport (Li et al. Reference Li, Xu, Wang, Yan, Zhang, Qian, Sun and Wang2022b). The pedestal density/collisionality and width scans for EAST indicate that small ELMs can be triggered by marginally unstable modes. These modes include low-n peeling modes, high-n ballooning modes, intermediate-n peeling-ballooning modes or a local ballooning instability in the pedestal foot, particularly in the presence of a larger separatrix density gradient (Li et al. Reference Li, Xu, Wang, Lin, Yan and Xu2022a). The size of the ELM, whether small or large, strongly depends on the inward avalanching and turbulence spreading from the linearly unstable zone to the stable zone during the nonlinear saturation phase (Li et al. Reference Li, Xu, Wang, Lin, Yan and Xu2022a). In the small/grassy ELM regime, the SOL turbulent thermal diffusivity increases due to larger turbulent fluxes being ejected from the pedestal into the SOL, resulting in a broadening of the SOL width (Li et al. Reference Li, Xu, Li, Chan and Wang2019; Xu et al. Reference Xu, Li, Li, Chen, Xia, Tang, Zhu and Chan2019b; Li et al. Reference Li, Xu, Hughes, Terry, Sun and Wang2020). Therefore, considering tokamak operational regimes with small ELMs may offer a potential solution to address the challenge of managing large transient heat loads in fusion reactors. However, several kept aspects of the underlying physics in the small ELM regime remain unclear. Questions persist regarding how to control the inward penetration and outward spreading phenomena, and how these processes influence the size of ELMs and the width of the SOL. Further investigation is crucial to understand the impact of turbulence spreading on the evolution of edge profiles and SOL width.
To investigate the impact of turbulence spreading on pedestal energy loss (ELM size) and heat flux width broadening in the small ELM regime, we conducted BOUT++ (Dudson et al. Reference Dudson, Umansky, Xu, Snyder and Wilson2009) turbulence simulations based on EAST experimental discharges, with variation in edge turbulence transport by altering the Er and SOL profiles. The remainder of this paper is organized as follows. The BOUT++ six-field, two-fluid physics model (Xia, Xu & Xi Reference Xia, Xu and Xi2013) and detailed simulation settings are introduced in § 2. The characteristics of avalanche and turbulence spreading phenomena in large and small ELMs are described in § 3. In § 4, the impact of Er on the turbulence spreading and the associated ELM size is investigated. The impact of SOL profiles on edge fluctuations and turbulence spreading is studied in § 5. The impact of the turbulence spreading on heat flux width in the small ELM regime is presented in § 6. Finally, § 7 gives the conclusions and discussions.
2. Physics models and simulation settings
In our simulations, the electromagnetic six-field, two-fluid model within the BOUT++ framework has been used to simulate the edge turbulent transport and divertor power deposition in EAST discharges. The perturbations of vorticity $\varpi$![]() , ion density ${n_i}$
, ion density ${n_i}$![]() , ion and electron temperature ${T_i}$
, ion and electron temperature ${T_i}$![]() and ${T_e}$
and ${T_e}$![]() , ion parallel velocity ${V_{{\parallel} i}}$
, ion parallel velocity ${V_{{\parallel} i}}$![]() , and parallel magnetic vector potential ${A_\parallel }$
, and parallel magnetic vector potential ${A_\parallel }$![]() are evolved to understand the ELM dynamics (Xia et al. Reference Xia, Xu and Xi2013). This model is based on the full set of Braginskii equations, which considers both ideal MHD and non-ideal physics effects, such as the stability of peeling-ballooning modes, ion diamagnetic effects, resistivity, hyper-resistivity, the first order ion finite Larmor radius effect due to the gyro-viscous stress tensor, parallel thermal conduction, Hall effects, toroidal compressibility, electron–ion friction, etc. In the simulations, the Spitzer resistivity with Zeff correction is used and the viscosity is spatially constant. Quasi-neutral condition is assumed. Sheath boundary conditions are included by assuming that the ion velocity matches the sound speed at the sheath boundary: ${V_{{\parallel} i}} = {C_s} = \sqrt {{k_B}({T_e} + {T_i})/{m_i}}$
are evolved to understand the ELM dynamics (Xia et al. Reference Xia, Xu and Xi2013). This model is based on the full set of Braginskii equations, which considers both ideal MHD and non-ideal physics effects, such as the stability of peeling-ballooning modes, ion diamagnetic effects, resistivity, hyper-resistivity, the first order ion finite Larmor radius effect due to the gyro-viscous stress tensor, parallel thermal conduction, Hall effects, toroidal compressibility, electron–ion friction, etc. In the simulations, the Spitzer resistivity with Zeff correction is used and the viscosity is spatially constant. Quasi-neutral condition is assumed. Sheath boundary conditions are included by assuming that the ion velocity matches the sound speed at the sheath boundary: ${V_{{\parallel} i}} = {C_s} = \sqrt {{k_B}({T_e} + {T_i})/{m_i}}$![]() . The sheath heat fluxes are
. The sheath heat fluxes are
where ${\gamma _e}$![]() and ${\gamma _i}$
and ${\gamma _i}$![]() are electron and ion sheath heat transmission factors, respectively. The temperature gradient is set by using the sheath heat flux divided by the parallel conductivity. Ion density and vorticity are set as the Neumann boundary condition in front of the target. In the radial direction, the Neumann boundary condition is applied on inner radial boundary surfaces while the Dirichlet boundary condition is used for the outer radial boundary surfaces for all the variables. For the pedestal region inside the LCFS, twist-shift periodic boundary conditions are set in the y direction along the magnetic field line and periodic boundary condition is used in the binormal direction. More detailed settings can be found in previous papers (Xia et al. Reference Xia, Xu and Xi2013; Xia & Xu Reference Xia and Xu2015). The flux-limiting parallel thermal conductivities (Malone, Mccrory & Morse Reference Malone, Mccrory and Morse1975) are used to approximate the kinetic correction of parallel transport for a transition from collisionless to collisional regimes. In the simulations, we initiate the process with small perturbations characterized by a broad spectrum and random phases. These perturbations receive their free energy from plasma gradients, leading to the development of linear instabilities. As these perturbations progress through the linear phase and grow to significant amplitudes, the influence of nonlinear physics becomes increasingly dominant, marking the transition into the nonlinear saturation phase. Consequently, our simulations encompass both linear and nonlinear phases. During the linear phase, it is possible to meticulously investigate the underlying sources of instability drivers, such as the ballooning mode, peeling mode, drift-Alfven mode, and more. However, during the nonlinear phase, we can delve into the characteristics of turbulence phenomena.
are electron and ion sheath heat transmission factors, respectively. The temperature gradient is set by using the sheath heat flux divided by the parallel conductivity. Ion density and vorticity are set as the Neumann boundary condition in front of the target. In the radial direction, the Neumann boundary condition is applied on inner radial boundary surfaces while the Dirichlet boundary condition is used for the outer radial boundary surfaces for all the variables. For the pedestal region inside the LCFS, twist-shift periodic boundary conditions are set in the y direction along the magnetic field line and periodic boundary condition is used in the binormal direction. More detailed settings can be found in previous papers (Xia et al. Reference Xia, Xu and Xi2013; Xia & Xu Reference Xia and Xu2015). The flux-limiting parallel thermal conductivities (Malone, Mccrory & Morse Reference Malone, Mccrory and Morse1975) are used to approximate the kinetic correction of parallel transport for a transition from collisionless to collisional regimes. In the simulations, we initiate the process with small perturbations characterized by a broad spectrum and random phases. These perturbations receive their free energy from plasma gradients, leading to the development of linear instabilities. As these perturbations progress through the linear phase and grow to significant amplitudes, the influence of nonlinear physics becomes increasingly dominant, marking the transition into the nonlinear saturation phase. Consequently, our simulations encompass both linear and nonlinear phases. During the linear phase, it is possible to meticulously investigate the underlying sources of instability drivers, such as the ballooning mode, peeling mode, drift-Alfven mode, and more. However, during the nonlinear phase, we can delve into the characteristics of turbulence phenomena.
In this paper, two EAST discharges of small/grassy ELMs with different poloidal magnetic field are studied. These are shot #103745 with lower-single null divertor configuration (Li et al. Reference Li, Xu, Wang, Lin, Yan and Xu2022a) and high poloidal magnetic field ${B_p}$![]() and #090949 with upper-single null divertor configuration (Li et al. Reference Li, Xu, Wang, Yan, Zhang, Qian, Sun and Wang2022b) and low ${B_p}$
and #090949 with upper-single null divertor configuration (Li et al. Reference Li, Xu, Wang, Yan, Zhang, Qian, Sun and Wang2022b) and low ${B_p}$![]() . These two shots are simulated to investigate the impact of turbulence spreading on the ELM size and divertor heat flux width. For shot #103745, the small ELM is triggered by the marginal intermediate-n peeling-ballooning instability (Li et al. Reference Li, Xu, Wang, Lin, Yan and Xu2022a). For shot #090949, the small ELM is triggered by the low-n peeling mode (Li et al. Reference Li, Xu, Wang, Yan, Zhang, Qian, Sun and Wang2022b). The simulations are radially global with both edge and SOL regions, which range from normalized poloidal flux ${\psi _n} = 0.75$
. These two shots are simulated to investigate the impact of turbulence spreading on the ELM size and divertor heat flux width. For shot #103745, the small ELM is triggered by the marginal intermediate-n peeling-ballooning instability (Li et al. Reference Li, Xu, Wang, Lin, Yan and Xu2022a). For shot #090949, the small ELM is triggered by the low-n peeling mode (Li et al. Reference Li, Xu, Wang, Yan, Zhang, Qian, Sun and Wang2022b). The simulations are radially global with both edge and SOL regions, which range from normalized poloidal flux ${\psi _n} = 0.75$![]() to ${\psi _n} = 1.05$
to ${\psi _n} = 1.05$![]() for shot #103745 and from ${\psi _n} = 0.8$
for shot #103745 and from ${\psi _n} = 0.8$![]() to ${\psi _n} = 1.1$
to ${\psi _n} = 1.1$![]() for shot #090949. The spatial resolution of the grid generated from the magnetic equilibrium file (kinetic EFIT g-file) is 260 radial grid points and 64 poloidal grid points. In the z-direction, 16 points are used for linear simulations and 64 points for nonlinear simulations. As for previous studies (Li et al. Reference Li, Xu, Wang, Lin, Yan and Xu2022a,Reference Li, Xu, Wang, Yan, Zhang, Qian, Sun and Wangb), the initial plasma profiles for these two discharges used in BOUT++ simulations are taken from fits of a modified hyperbolic tanh function (Groebner & Osborne Reference Groebner and Osborne1998) to experimental data, mapped onto a radial coordinate of normalized poloidal magnetic flux with the SOL region, as shown by figure 1. However, due to the diagnostics limitation, the experimental data in the SOL sometime are not available. Therefore, we usually assume a flat or a small gradient profile from separatrix to outer boundary. To investigate the effect of SOL profiles on the edge turbulence transport and heat flux width, comparisons between flat and steep SOL profiles are presented in § 5, for shot #103745. In general, in our simulations, there is no radial electric field (Er) profile provided from the experimental measurements. Therefore, Er is calculated from force balance with the ion pressure ${P_{i0}}$
for shot #090949. The spatial resolution of the grid generated from the magnetic equilibrium file (kinetic EFIT g-file) is 260 radial grid points and 64 poloidal grid points. In the z-direction, 16 points are used for linear simulations and 64 points for nonlinear simulations. As for previous studies (Li et al. Reference Li, Xu, Wang, Lin, Yan and Xu2022a,Reference Li, Xu, Wang, Yan, Zhang, Qian, Sun and Wangb), the initial plasma profiles for these two discharges used in BOUT++ simulations are taken from fits of a modified hyperbolic tanh function (Groebner & Osborne Reference Groebner and Osborne1998) to experimental data, mapped onto a radial coordinate of normalized poloidal magnetic flux with the SOL region, as shown by figure 1. However, due to the diagnostics limitation, the experimental data in the SOL sometime are not available. Therefore, we usually assume a flat or a small gradient profile from separatrix to outer boundary. To investigate the effect of SOL profiles on the edge turbulence transport and heat flux width, comparisons between flat and steep SOL profiles are presented in § 5, for shot #103745. In general, in our simulations, there is no radial electric field (Er) profile provided from the experimental measurements. Therefore, Er is calculated from force balance with the ion pressure ${P_{i0}}$![]() without net flow, ${E_r} = 1/({n_0}{Z_i}e)\boldsymbol{\nabla }{P_{i0}}$
without net flow, ${E_r} = 1/({n_0}{Z_i}e)\boldsymbol{\nabla }{P_{i0}}$![]() . This so-called diamagnetic Er is shown in figure 2. To study the impact of the Er profile on the edge turbulence and divertor heat flux width, both linear and nonlinear simulations for the pedestal Er scan are performed for shot #103745 in § 4.1. To study the effect of SOL E × B shear on the divertor heat flux width, two nonlinear simulations are compared for different SOL Er profiles in § 4.2 for shot #090949. In this section, the two-dimensional (2-D) Er profile is self-consistently calculated by the BOUT++ transport model (Li et al. Reference Li, Xu, Rognlien, Gui, Sun and Wang2018) with sheath boundary conditions on the divertor plates.
. This so-called diamagnetic Er is shown in figure 2. To study the impact of the Er profile on the edge turbulence and divertor heat flux width, both linear and nonlinear simulations for the pedestal Er scan are performed for shot #103745 in § 4.1. To study the effect of SOL E × B shear on the divertor heat flux width, two nonlinear simulations are compared for different SOL Er profiles in § 4.2 for shot #090949. In this section, the two-dimensional (2-D) Er profile is self-consistently calculated by the BOUT++ transport model (Li et al. Reference Li, Xu, Rognlien, Gui, Sun and Wang2018) with sheath boundary conditions on the divertor plates.

Figure 1. Initial profiles of total pressure (black) and parallel current (red) for shot (a) #103745 and (b) #090949. Here the dashed curves are at the location of peak total pressure gradient with ${\psi _n} = 0.93$![]() for shot #103745 and ${\psi _n} = 0.949$
for shot #103745 and ${\psi _n} = 0.949$![]() for shot #090949.
for shot #090949.

Figure 2. Radial electric field at outer midplane (OMP) for shot (a) #103745 and (b) #090949.
3. Characteristics of avalanche and turbulence spreading phenomena in large and small ELMs
Avalanche is originally used to describe a mass of snow, rock and/or ice falling down a mountain or incline, such as a snow avalanche. Turbulence spreading is typically used to describe the decoupling of local turbulence intensity or turbulent diffusivity from the local profile gradient. Both result in a deviation from local transport models. Here we report the non-local transport characteristics of the avalanches and turbulence spreading (Hahm & Diamond Reference Hahm and Diamond2018) generated during the collapse of a pedestal transport barrier in large and small ELMs.
BOUT++ turbulence simulations (Li et al. Reference Li, Xu, Wang, Lin, Yan and Xu2022a) for a scan of pedestal density/collisionality and pedestal width show that the small ELM can be triggered near marginal instability in the pedestal by low-n peeling modes, intermediate-n peeling-ballooning modes or high-n ballooning modes. Whether the ELM is small or large strongly depends on the inward spreading of the edge fluctuation intensity. For large ELMs (shot #103751 for EAST) with diamagnetic Er effect, the linear mode is very unstable with a large linear growth rate in the pedestal. A strong avalanche process occurs with multiple pedestal collapse events, as shown by figure 3. Here the solid curves show the total pressure profiles, while the dashed curves are normalized total pressure fluctuation intensity ${(\tilde{p}/p)^2}$![]() for large ELMs at different times during an ELM crash. In the linear phase, the mode first grows up at the peak gradient of total pressure, as shown by the black curves. Due to the large linear growth rate, the ELM is soon triggered and the profile crashes, as shown from the black to the red curve. The profile steepening shifts inward, resulting in linear instability there, and a second pedestal crash occurs. The pressure profile keeps crashing up to the pedestal top, as shown from the black to the red, blue and green curves, leading to fast front propagation (as black arrow indicates in figure 3) and deep inward penetration (as red arrow indicates in figure 3). The pedestal ELM energy loss for large ELM is much stronger with a large ELM size $\Delta {W_{\textrm{ped}}}/{W_{\textrm{ped}}} \gg 1\,\%$
for large ELMs at different times during an ELM crash. In the linear phase, the mode first grows up at the peak gradient of total pressure, as shown by the black curves. Due to the large linear growth rate, the ELM is soon triggered and the profile crashes, as shown from the black to the red curve. The profile steepening shifts inward, resulting in linear instability there, and a second pedestal crash occurs. The pressure profile keeps crashing up to the pedestal top, as shown from the black to the red, blue and green curves, leading to fast front propagation (as black arrow indicates in figure 3) and deep inward penetration (as red arrow indicates in figure 3). The pedestal ELM energy loss for large ELM is much stronger with a large ELM size $\Delta {W_{\textrm{ped}}}/{W_{\textrm{ped}}} \gg 1\,\%$![]() , where $\Delta {W_{\textrm{ped}}} = \int_{{R_{\textrm{in}}}}^{{R_{\textrm{out}}}} {\mathrm{\oint }\,\textrm{d}R\,\textrm{d}\theta ({P_0} - {P_\zeta })}$
, where $\Delta {W_{\textrm{ped}}} = \int_{{R_{\textrm{in}}}}^{{R_{\textrm{out}}}} {\mathrm{\oint }\,\textrm{d}R\,\textrm{d}\theta ({P_0} - {P_\zeta })}$![]() is the ELM energy loss and ${W_{\textrm{ped}}} = {\textstyle{3 \over 2}}{P_{\textrm{ped}}}V$
is the ELM energy loss and ${W_{\textrm{ped}}} = {\textstyle{3 \over 2}}{P_{\textrm{ped}}}V$![]() is the pedestal stored energy. The symbol ${P_0}$
is the pedestal stored energy. The symbol ${P_0}$![]() is the equilibrium pressure; ${P_\zeta }$
is the equilibrium pressure; ${P_\zeta }$![]() is the toroidal average of perturbed pressure; ${R_{\textrm{in}}}$
is the toroidal average of perturbed pressure; ${R_{\textrm{in}}}$![]() is at the inner boundary of simulated radial domain; ${R_{\textrm{in}}}$
is at the inner boundary of simulated radial domain; ${R_{\textrm{in}}}$![]() is at outer boundary and ${P_{\textrm{ped}}}$
is at outer boundary and ${P_{\textrm{ped}}}$![]() is the pedestal pressure. While for small ELMs with diamagnetic Er effect, there is no clear front propagation for normalized pressure fluctuation intensity as shown in figure 4. Here the black curves are at linear phase (before the ELM crashes), while the red curves are the time average at the nonlinear phase for shot #103745. The time average in the nonlinear phase is for the red curves. The mode grows up first at the peak gradient position driven by the marginal unstable peeling-ballooning (P-B) modes. The small ELM is triggered on a long time scale due to the small linear growth rate. The fluctuation intensity saturates at a low level, in comparison with that of the large ELM. The pedestal profile relaxes below the P-B instability threshold after the initial ELM crash. Therefore, the peak location of the mode will stay at the same location before and after the ELM crash, leading to small ELMs. The pedestal ELM energy loss fraction for small ELMs is much weaker than that of large ELMs. For the small ELM, the ELM size is ~1 %. Even though there is no clear front propagation and turbulence spreading is limited to within the pedestal, there is still inward penetration (as red arrow indicates in figure 4) for the small ELM.
is the pedestal pressure. While for small ELMs with diamagnetic Er effect, there is no clear front propagation for normalized pressure fluctuation intensity as shown in figure 4. Here the black curves are at linear phase (before the ELM crashes), while the red curves are the time average at the nonlinear phase for shot #103745. The time average in the nonlinear phase is for the red curves. The mode grows up first at the peak gradient position driven by the marginal unstable peeling-ballooning (P-B) modes. The small ELM is triggered on a long time scale due to the small linear growth rate. The fluctuation intensity saturates at a low level, in comparison with that of the large ELM. The pedestal profile relaxes below the P-B instability threshold after the initial ELM crash. Therefore, the peak location of the mode will stay at the same location before and after the ELM crash, leading to small ELMs. The pedestal ELM energy loss fraction for small ELMs is much weaker than that of large ELMs. For the small ELM, the ELM size is ~1 %. Even though there is no clear front propagation and turbulence spreading is limited to within the pedestal, there is still inward penetration (as red arrow indicates in figure 4) for the small ELM.

Figure 3. Radial total pressure profiles (solid curves) and normalized total pressure fluctuation intensity (dashed curves) at outer midplane for large ELM (shot #103751) at different time slices. Here the black curves are in the linear phase at $t = 60{\tau _A}$![]() with ${\tau _A} = 4.45 \times {10^{ - 7}}\ \textrm{s}$
with ${\tau _A} = 4.45 \times {10^{ - 7}}\ \textrm{s}$![]() ; the red, blue and green curves are in the nonlinear phase at $t = 80{\tau _A}$
; the red, blue and green curves are in the nonlinear phase at $t = 80{\tau _A}$![]() , $t = 150{\tau _A}$
, $t = 150{\tau _A}$![]() , $t = 310{\tau _A}$
, $t = 310{\tau _A}$![]() , respectively.
, respectively.

Figure 4. Radial total pressure profiles (solid curves) and normalized total pressure fluctuation intensity (dashed curves) at outer midplane in the linear (black curves) and the nonlinear phase (red curves) for small ELM (shot#103745).
Overall, these two special cases highlight the distinct characteristics of the large and small ELMs. (1) For larger ELMs, the triggering process occurs rapidly with a substantial linear growth rate, leading to a strong avalanche process and inward spreading during the nonlinear phase. These ELMs have a significant size with $\Delta {W_{\textrm{ped}}}/{W_{\textrm{ped}}} \gg 1\,\textrm{\%}$![]() . (2) In contrast, small ELMs are triggered over a long time scale with a small linear growth rate. During the nonlinear phase, the peak of edge fluctuation intensity remains in the same radial location before and after the ELM crash. There is no clear front propagation, but instead, an inward penetration with small ELM size ~1 %. To further explore the impact of turbulence spreading on the pedestal dynamics and SOL radial transport, we conducted an Er scan to study the inward spreading by changing the unstable modes, which reveals the transition from small to large ELMs. Section 4 will discuss in detail the Er effect on the inward spreading. Additionally, regardless of the ELM size, we observed that during the ELM crash, energy is transported from the pedestal into the SOL. The phenomenon of strong outer fluctuation spreading occurs for both large and small ELMs, as shown by the blue arrows in figures 3 and 4. This enhances the radial turbulence transport, resulting in SOL width broadening. Section 6 will provide a more comprehensive analysis of the effect of outward turbulence spreading on the heat flux width.
. (2) In contrast, small ELMs are triggered over a long time scale with a small linear growth rate. During the nonlinear phase, the peak of edge fluctuation intensity remains in the same radial location before and after the ELM crash. There is no clear front propagation, but instead, an inward penetration with small ELM size ~1 %. To further explore the impact of turbulence spreading on the pedestal dynamics and SOL radial transport, we conducted an Er scan to study the inward spreading by changing the unstable modes, which reveals the transition from small to large ELMs. Section 4 will discuss in detail the Er effect on the inward spreading. Additionally, regardless of the ELM size, we observed that during the ELM crash, energy is transported from the pedestal into the SOL. The phenomenon of strong outer fluctuation spreading occurs for both large and small ELMs, as shown by the blue arrows in figures 3 and 4. This enhances the radial turbulence transport, resulting in SOL width broadening. Section 6 will provide a more comprehensive analysis of the effect of outward turbulence spreading on the heat flux width.
It is worth noting that in these two simulations, we employed the diamagnetic Er. However, edge Er plays a crucial role in setting the edge turbulence transport. To investigate the influence of edge Er on the turbulence spreading, we conducted an Er scan in § 4 with two EAST small ELM discharges.
4. Impact of Er on the edge dynamics
The edge E × B shear plays an important role in setting the edge turbulence transport. BOUT++ simulations have revealed that in the ELMy H-mode operation, the E × B shear flow can stabilize the high-n ballooning modes while inducing the Kelvin–Helmholtz instabilities through bootstrap current and rotational shear (Chen et al. Reference Chen, Xu, Ma, Xi, Kong and Lei2017; Zhang, Guo & Diamond Reference Zhang, Guo and Diamond2020). The stability of the pedestal plasmas and ELM dynamics are the outcome of the competition between these two effects. As discussed in § 3, the ELM size strongly depends on the inward spreading of edge turbulence. To study the impact of inward spreading on the ELM size and understand the transition from small to large ELMs, we conducted a series of BOUT++ nonlinear simulations with different Er profiles. Section 4.1 presents the results of a pedestal Er scan, focusing on the impact of turbulence spreading on ELM size. Furthermore, in § 4.2, we examine the impact of SOL E × B shear on the turbulence spreading. These simulations and analysis contribute to a deeper understanding of the underlying mechanisms driving the behaviour of ELM dynamics.
4.1. Edge Er scan for small ELMs
According to the radial force balance, the Er can be calculated by ${E_r} = E_r^{\textrm{dia}} + E_r^{V \times B}$![]() . Here $E_r^{\textrm{dia}}$
. Here $E_r^{\textrm{dia}}$![]() represents the diamagnetic component given by $E_r^{\textrm{dia}} = \boldsymbol{\nabla }{P_{i0}}/{n_0}{Z_i}e$
represents the diamagnetic component given by $E_r^{\textrm{dia}} = \boldsymbol{\nabla }{P_{i0}}/{n_0}{Z_i}e$![]() and $E_r^{V \times B}$
and $E_r^{V \times B}$![]() corresponds to the ion flow component, $E_r^{V \times B} = \boldsymbol{V} \times \boldsymbol{B}$
corresponds to the ion flow component, $E_r^{V \times B} = \boldsymbol{V} \times \boldsymbol{B}$![]() . Additionally, ${P_{i0}}$
. Additionally, ${P_{i0}}$![]() is the ion pressure and ${Z_i}$
is the ion pressure and ${Z_i}$![]() is the charge number. Consequently, the pedestal E × B flow shear can be altered by modulating either the ion pressure profile or the toroidal plasma flow profile. In general, the pressure profile serves a dual role: (1) its gradient can drive edge MHD modes; and (2) its curvature can induce an E × B shear, which suppresses the underlying instabilities. While the pressure profile remains fixed for a given equilibrium from experiments, the pedestal Er can be modified by toroidal plasma rotation, which can in turn modulate the E × B shearing profile without altering the pressure gradient. Therefore, with a given equilibrium from experiments, the pressure profile keeps constant. In our simulations, to modify the E × B shearing profile, we perform an Er scan by multiplying the diamagnetic $E_r^{\textrm{dia}}$
is the charge number. Consequently, the pedestal E × B flow shear can be altered by modulating either the ion pressure profile or the toroidal plasma flow profile. In general, the pressure profile serves a dual role: (1) its gradient can drive edge MHD modes; and (2) its curvature can induce an E × B shear, which suppresses the underlying instabilities. While the pressure profile remains fixed for a given equilibrium from experiments, the pedestal Er can be modified by toroidal plasma rotation, which can in turn modulate the E × B shearing profile without altering the pressure gradient. Therefore, with a given equilibrium from experiments, the pressure profile keeps constant. In our simulations, to modify the E × B shearing profile, we perform an Er scan by multiplying the diamagnetic $E_r^{\textrm{dia}}$![]() by a factor 1.0×, 1.5×, 2×, 2.5×, while keeping the pressure profile fixed for EAST shot #103745, as shown by figure 5(a). The black curve is the diamagnetic $E_r^{\textrm{dia}}$
by a factor 1.0×, 1.5×, 2×, 2.5×, while keeping the pressure profile fixed for EAST shot #103745, as shown by figure 5(a). The black curve is the diamagnetic $E_r^{\textrm{dia}}$![]() , determined by the pressure gradient and density profile. Essentially, the Er scan is equivalent to the plasma flow $\boldsymbol{V}$
, determined by the pressure gradient and density profile. Essentially, the Er scan is equivalent to the plasma flow $\boldsymbol{V}$![]() or $E_r^{V \times B}$
or $E_r^{V \times B}$![]() scan with specific flow profiles, generating the same profiles as the diamagnetic Er, but with varying magnitudes. We label these four cases as Er1.0BLACK, Er1.5RED, Er2.0BLUE, Er2.5GREEN, respectively, corresponding to $E_r^{V \times B} = 0$
scan with specific flow profiles, generating the same profiles as the diamagnetic Er, but with varying magnitudes. We label these four cases as Er1.0BLACK, Er1.5RED, Er2.0BLUE, Er2.5GREEN, respectively, corresponding to $E_r^{V \times B} = 0$![]() , $E_r^{V \times B} = 0.5E_r^{\textrm{dia}}$
, $E_r^{V \times B} = 0.5E_r^{\textrm{dia}}$![]() , $E_r^{V \times B} = 1.0E_r^{\textrm{dia}}$
, $E_r^{V \times B} = 1.0E_r^{\textrm{dia}}$![]() , $E_r^{V \times B} = 1.5E_r^{\textrm{dia}}$
, $E_r^{V \times B} = 1.5E_r^{\textrm{dia}}$![]() . Furthermore, the corresponding E × B shearing rate ${\omega _{E \times B}}$
. Furthermore, the corresponding E × B shearing rate ${\omega _{E \times B}}$![]() is calculated by using the expression ${\omega _{E \times B}} = ({(R{B_p})^2}/B)(\partial /\partial \varphi )({E_r}/R{B_p})$
is calculated by using the expression ${\omega _{E \times B}} = ({(R{B_p})^2}/B)(\partial /\partial \varphi )({E_r}/R{B_p})$![]() , as shown by figure 5(b). The E × B shearing rate increases as the Er well deepens.
, as shown by figure 5(b). The E × B shearing rate increases as the Er well deepens.

Figure 5. (a) Radial electric field (Er) profiles and (b) normalized E × B shear rate at outer midplane for Er scan with shot #103745.
To gain insights into the dominant modes under different Er conditions, we conduct linear simulations by turning off the nonlinear terms in the equations. The linear simulations initiate from small random perturbations. Figure 6 shows the linear growth rate versus toroidal mode number n for the Er scan. For the case with the diamagnetic Er, represented by the black curve in figure 6, the pedestal exhibits marginally instability attributed to the peeling-ballooning mode with n ~ 40. However, for the case Er1.5RED scenario, the high-n modes are stabilized, whereas the low-n modes become destabilized. Consequently, the dominant modes shift from n ~ 40 to n ~ 15–25 while the mode spectrum narrowed, the largest linear growth rate has almost no change. As we further deepen the Er, the low-n peeling modes become more sensitive to Er and are strongly destabilized by its influence. Consequently, the dominant mode shifts to the low-n peeling modes, leading to a narrow mode spectrum and a significant increase in the linear growth rate. Particularly, for the case Er2.5GREEN, a large crash is observed compared with the other cases. The results of these linear simulations, indicating that the stabilization of high-n modes and destabilization of low-n modes by strong E × B flow shear, are in excellent agreement with previous BOUT++ work conducted in a circular geometry, as referenced by Chen et al. (Reference Chen, Xu, Ma, Xi, Kong and Lei2017) and Zhang et al. (Reference Zhang, Guo and Diamond2020). These findings contribute to our understanding of the behaviour of dominant modes under varying Er shearing conditions.

Figure 6. Linear growth rate versus toroidal mode number with different Er.
To investigate the impact of the Er effect on the edge turbulence spreading, the nonlinear turbulence simulations are conducted to capture the underlying physics of the ELM dynamics under different Er profiles. The nonlinear simulations are performed using the same simulation settings as the linear simulations, with the only difference being activation of all nonlinear terms. To thoroughly explore both inward penetration and outward spreading, the radial simulation domain covers a range from normalized poloidal flux ${\psi _n} = 0.75$![]() to ${\psi _n} = 1.05$
to ${\psi _n} = 1.05$![]() for all these four cases, with the separatrix positioned at ${\psi _n} = 1.0$
for all these four cases, with the separatrix positioned at ${\psi _n} = 1.0$![]() .
.
The pressure fluctuation intensity at the outer midplane is calculated in both the linear and nonlinear phase for these four cases from the simulations. Figure 7 presents the results, showing the normalized pressure fluctuation intensity at the outer midplane for linear (solid curves) and nonlinear phase (dashed curves) with different Er. In all cases, the pedestal peak pressure gradient position is unstable to peeling-ballooning modes and the mode grows at that position observed in the linear phase (solid curves in figure 7). However, with deeper Er wells, the linear growth rate increases and fluctuation intensity at the onset of ELM increases, leading to enhanced inward spreading. This trend is evident in the dashed curves in figure 7, showing increasing inward penetration. As inward penetration increases, the ELM size increases, as shown in figure 8. A comparison of the case Er2.5GREEN with the other three cases (Er1.0BLACK, Er1.5RED, Er2.0BLUE) reveals a notable shift inward of the mode's peak location after the initial ELM crash. The strong avalanche process in the case Er2.5GREEN results in a large ELM crash. In contrast, for the cases from Er1.0 to Er2.0, although the inward turbulence spreading is enhanced due to deeper Er wells induced by E × B net flow, the pedestal stabilizes linearly after the initial ELM crash. Consequently, the dominant mode in the nonlinear phase remains at the same location as in the linear phase, thus resulting in a small ELM.

Figure 7. Normalized pressure fluctuation intensity at outer midplane in the linear (solid) and nonlinear phase (dashed) with different Er.

Figure 8. Inward turbulence spreading depth $\Delta {\psi _n}$![]() versus ELM size for Er scan.
versus ELM size for Er scan.
To quantify the ELM size increasing due to inward penetration, the inward turbulence spreading depth $\Delta {\psi _n}$![]() is calculated by $\Delta {\psi _n} = {\varDelta _{\textrm{nonlinear}}} - {\varDelta _{\textrm{linear}}}$
is calculated by $\Delta {\psi _n} = {\varDelta _{\textrm{nonlinear}}} - {\varDelta _{\textrm{linear}}}$![]() . Here ${\varDelta _{\textrm{linear}}}$
. Here ${\varDelta _{\textrm{linear}}}$![]() is the penetration depth in the linear phase, while ${\varDelta _{\textrm{nonlinear}}}$
is the penetration depth in the linear phase, while ${\varDelta _{\textrm{nonlinear}}}$![]() is the penetration depth in the nonlinear phase. The penetration depth Δ is defined as the point where the front foot starts to decrease to 10−2 of the peak fluctuation intensity level, as defined by Li et al. (Reference Li, Xu, Wang, Lin, Yan and Xu2022a). Figure 8 shows the relation between ELM size with inward turbulence spreading depth $\Delta {\psi _n}$
is the penetration depth in the nonlinear phase. The penetration depth Δ is defined as the point where the front foot starts to decrease to 10−2 of the peak fluctuation intensity level, as defined by Li et al. (Reference Li, Xu, Wang, Lin, Yan and Xu2022a). Figure 8 shows the relation between ELM size with inward turbulence spreading depth $\Delta {\psi _n}$![]() . The ELM size exhibits a strong dependence on $\Delta {\psi _n}$
. The ELM size exhibits a strong dependence on $\Delta {\psi _n}$![]() . In the small ELM regime (black, red, blue stars in figure 8), the ELM size increases linearly with increasing $\Delta {\psi _n}$
. In the small ELM regime (black, red, blue stars in figure 8), the ELM size increases linearly with increasing $\Delta {\psi _n}$![]() . For example, the ELM size increases by ~2.4 times from case Er1.0 to Er2.0, with $\Delta {\psi _n}$
. For example, the ELM size increases by ~2.4 times from case Er1.0 to Er2.0, with $\Delta {\psi _n}$![]() increasing ~2.25 times. However, with the transition from small to large ELMs, the ELM size dramatically increases from Er2.0 to Er2.5 due to the stronger avalanche process. Our simulations demonstrate a positive correlation between ELM size and inward turbulence spreading depth, which corresponds to the extension of the area affected by the ELM, consistent with experimental measurements (Loarte et al. Reference Loarte2007; Kojima et al. Reference Kojima, Oyama, Sakamoto, Kamada, Urano, Kamiya, Fujita, Kubo and Aiba2009). The narrow radial extent of the density pedestal collapse due to grassy ELMs, as confirmed by fast density profile measurement using a lithium beam probe (LiBP) (Kojima et al. Reference Kojima, Oyama, Sakamoto, Kamada, Urano, Kamiya, Fujita, Kubo and Aiba2009), agrees with our simulation results. Further studies of avalanche and turbulence spreading will offer valuable insights for determining the ELM affected area and, consequently, aid in developing ELM control strategies.
increasing ~2.25 times. However, with the transition from small to large ELMs, the ELM size dramatically increases from Er2.0 to Er2.5 due to the stronger avalanche process. Our simulations demonstrate a positive correlation between ELM size and inward turbulence spreading depth, which corresponds to the extension of the area affected by the ELM, consistent with experimental measurements (Loarte et al. Reference Loarte2007; Kojima et al. Reference Kojima, Oyama, Sakamoto, Kamada, Urano, Kamiya, Fujita, Kubo and Aiba2009). The narrow radial extent of the density pedestal collapse due to grassy ELMs, as confirmed by fast density profile measurement using a lithium beam probe (LiBP) (Kojima et al. Reference Kojima, Oyama, Sakamoto, Kamada, Urano, Kamiya, Fujita, Kubo and Aiba2009), agrees with our simulation results. Further studies of avalanche and turbulence spreading will offer valuable insights for determining the ELM affected area and, consequently, aid in developing ELM control strategies.
To further investigate the impact of different Er on inward and outward turbulence spreading, we analyse the probability distribution functions (p.d.f.s) of fluctuation energy flux ${\varGamma _\varXi } = {V_r}\ast ({\tilde{p}^2})$![]() in the nonlinear phase at various radial locations (Li et al. Reference Li, Xu, Diamond, Zhang, Liu, Wang, Yan and Xu2023). Figure 9 illustrates the p.d.f.s at the peak pressure gradient position (figure 9a) and at the pedestal top with ${\psi _n} = 0.85$
in the nonlinear phase at various radial locations (Li et al. Reference Li, Xu, Diamond, Zhang, Liu, Wang, Yan and Xu2023). Figure 9 illustrates the p.d.f.s at the peak pressure gradient position (figure 9a) and at the pedestal top with ${\psi _n} = 0.85$![]() (figure 9b). Positive values represent outward spreading, while the negative values indicate inward penetration. At the peak pressure gradient position, particularly near the inner edge of the Er well, we observe that with deeper Er wells, the E × B shear flow increases, driving strong linear instabilities, as shown in figure 6, and leading to strong avalanche and turbulence spreading, resulting in a large ELM crash. As a consequence, the p.d.f. becomes broadened on both sides, reflecting enhanced both inward and outward spreading, as shown by figure 9(a). Therefore, the inward penetration increases, as also demonstrated in figure 7. However, at ${\psi _n} = 0.85$
(figure 9b). Positive values represent outward spreading, while the negative values indicate inward penetration. At the peak pressure gradient position, particularly near the inner edge of the Er well, we observe that with deeper Er wells, the E × B shear flow increases, driving strong linear instabilities, as shown in figure 6, and leading to strong avalanche and turbulence spreading, resulting in a large ELM crash. As a consequence, the p.d.f. becomes broadened on both sides, reflecting enhanced both inward and outward spreading, as shown by figure 9(a). Therefore, the inward penetration increases, as also demonstrated in figure 7. However, at ${\psi _n} = 0.85$![]() , only the Er2.5 case displays a large tail in the p.d.f. of fluctuation energy flux ${\varGamma _\varXi }$
, only the Er2.5 case displays a large tail in the p.d.f. of fluctuation energy flux ${\varGamma _\varXi }$![]() , indicating strong inward and outward turbulent transport in the pedestal top, and leading to a large ELM. In contrast, the other three cases show only a small tail in the p.d.f., suggesting limited turbulence spreading, resulting in small ELMs.
, indicating strong inward and outward turbulent transport in the pedestal top, and leading to a large ELM. In contrast, the other three cases show only a small tail in the p.d.f., suggesting limited turbulence spreading, resulting in small ELMs.

Figure 9. Probability distribution functions (p.d.f.s) of fluctuation energy flux ${\varGamma _\varXi } = {V_r}{(\tilde{p})^2}$![]() in nonlinear phase (a) at peak pressure gradient position with ${\psi _n} = 0.93$
in nonlinear phase (a) at peak pressure gradient position with ${\psi _n} = 0.93$![]() and (b) at pedestal top ${\psi _n} = 0.85$
and (b) at pedestal top ${\psi _n} = 0.85$![]() .
.
In § 6, we will further investigate the relationship between outward turbulence spreading and the SOL width for different Er profiles.
4.2. The impact of local SOL Er on the turbulence spreading
In the pedestal region, Er is primarily determined by radial force balance. However, in the SOL, Er is strongly influenced by the SOL physics, such as the sheath boundary conditions. In § 4.1, we find a significant effect of pedestal Er on both pedestal instability, and inward and outward turbulence spreading. However, the impact of SOL Er on these processes remains less clear.
To explore the impact of local SOL Er on turbulence spreading, Er is self-consistently calculated using the BOUT++ 2-D transport module (Li et al. Reference Li, Xu, Rognlien, Gui, Sun and Wang2018). The simulation domain covers from the pedestal to the SOL. The BOUT++ 2-D transport module is distinct from the six-field, two-fluid turbulence module, and it includes the equations for ion density, ion momentum, and energy for both the electrons and ions based on Braginskii equations. By including cross-field drifts effects, the module yields steady-state 2-D plasma and Er profiles across the separatrix. The plasma profiles inside the separatrix match experimentally measured profiles, while the Er profiles inside the separatrix are consistent with those determined by radial force balance. Additional details about this module can be found in previous papers (Li et al. Reference Li, Xu, Rognlien, Gui, Sun and Wang2018, Reference Li, Xu, Hughes, Terry, Sun and Wang2020).
In this study, the role of transport module is to establish the 2-D initial plasma profiles in the SOL and determine the Er profile across the separatrix for turbulence simulations.
The edge Er is determined by the force balance in the pedestal inside the separatrix and by the sheath boundary condition in the SOL. Figure 10 shows the Er profile and the corresponding E × B shearing rate for EAST shot #090949. The red curve represents the diamagnetic Er induced by the ion pressure gradient, while the blue curve represents the Er simulated using the BOUT++ transport module. Notably, a large positive Er is formed in the SOL due to the SOL physics and the sheath boundary conditions, as shown by the blue curve in figure 10(a). Inside the separatrix, Er is mainly determined by the ion force balance. The ion viscous effect smoothly connects the pedestal Er and the SOL Er across the separatrix of the order of the ion gyro-radius scale, resulting in the identical Er shape in the main pedestal region with diamagnetic Er. Therefore, a large E × B shearing rate arises from the positive Er in the SOL, with a marginal decrease observed in the inner edge of the Er well, as shown in figure 10(b).

Figure 10. (a) Radial electric field profiles and (b) Er shear rate at outer midplane with (blue) and without (red) sheath boundary conditions for shot #090949.
To compare the effect of local E × B flow shear on the edge turbulence spreading, we employ 2-D plasma and Er profiles calculated from the BOUT++ transport module as inputs for BOUT++ six-field two-fluid turbulence nonlinear simulations.
The nonlinear simulations for shot #090949 with upper-single null divertor configuration show that the pedestal energy loss or the ELM size increases approximately 20 % when using the Er from simulations of the BOUT++ transport module, compared to the diamagnetic Er. This is shown by the blue curve in figure 11(b). Moreover, when using the Er from the simulation of transport module, the Er inside the pedestal decreases, and the E × B shearing rate slightly decreases as well when compared to the diamagnetic Er. The decrease in pedestal Er destabilizes the pedestal and enhance the inward spreading of pedestal turbulence. As shown in figure 11(a), the inward penetration increases, leading to a large ELM size, as shown in figure 11(b). This stands in contrast to the findings in § 4.1, where the effect of Er on the pedestal instability is opposite. Specifically, when the Er is smaller than the diamagnetic Er, a negative E × B shear flow is induced, resulting in the destabilizing effect on the pedestal instability. As pedestal Er decreases to smaller than diamagnetic Er, the linear growth rate increases, but with the same dominant mode, thereby inducing pedestal instability in both co- and counter direction of E × B shear flow. In summary, the pedestal Er scan indicates that changing the pedestal Er profile can enhance pedestal instability, consistent with experiment results, where strong turbulence can be triggered by NBI in both co- and counter direction (Burrell et al. Reference Burrell2005, Reference Burrell, Osborne, Snyder, West, Fenstermacher, Groebner, Gohil, Leonard and Solomon2009; Chen et al. Reference Chen2016).

Figure 11. (a) Normalized pressure fluctuation intensity at outer midplane in the linear phase (black solid curve) and nonlinear phase (dashed curves) with different Er; (b) time evolution of 3-D energy loss fraction (ELM size) with different Er. The red curves are with diamagnetic Er while the blue curves are with Er calculated by the BOUT++ transport module.
To compare the effect of local SOL Er on inward and outward spreading at different radial location, the p.d.f.s of fluctuation energy flux ${\varGamma _\varXi } = {V_r}\ast {(\tilde{p})^2}$![]() in nonlinear phase are calculated at the peak pressure gradient position and at the separatrix, as shown in figure 12. At the peak gradient location of the pedestal (figure 12a), the p.d.f. shift towards to the negative value, indicating an increase in inward fluctuation energy flux and inward turbulence spreading. However, the positive fluctuation energy flux remains almost unchanged, and outward turbulence spreading is limited due to the strong E × B shearing rate at the pedestal bottom. Near the separatrix (figure 12b), both inward and outward energy flux decrease, resulting in smaller fluctuation, as shown by the dashed curves in figure 11(a). The blue dashed curve lies below the red dashed curve outside the peak pressure gradient location due to the suppression of turbulence spreading by the strong E × B shearing rate near the separatrix. Thus, the local SOL Er can influence the turbulence spreading.
in nonlinear phase are calculated at the peak pressure gradient position and at the separatrix, as shown in figure 12. At the peak gradient location of the pedestal (figure 12a), the p.d.f. shift towards to the negative value, indicating an increase in inward fluctuation energy flux and inward turbulence spreading. However, the positive fluctuation energy flux remains almost unchanged, and outward turbulence spreading is limited due to the strong E × B shearing rate at the pedestal bottom. Near the separatrix (figure 12b), both inward and outward energy flux decrease, resulting in smaller fluctuation, as shown by the dashed curves in figure 11(a). The blue dashed curve lies below the red dashed curve outside the peak pressure gradient location due to the suppression of turbulence spreading by the strong E × B shearing rate near the separatrix. Thus, the local SOL Er can influence the turbulence spreading.

Figure 12. Probability distribution functions (p.d.f.s) of energy flux ${V_r}\ast {(\tilde{p})^2}$![]() in the nonlinear phase (a) at peak gradient of pressure with ${\psi _n} = 0.95$
in the nonlinear phase (a) at peak gradient of pressure with ${\psi _n} = 0.95$![]() and (b) at separatrix.
and (b) at separatrix.
It is important to note that in these simulations, flat SOL profiles are assumed. The effect of local SOL profiles on the pedestal instability will be discussed in § 5, while the strong local E × B shearing rate's effect on outward turbulence spreading and the SOL width will be discussed in § 6.
5. Impact of SOL profiles on pedestal dynamics
In the previous sections, we analysed the transport of the fluctuation intensity from the pedestal to the SOL, effectively transferring it from unstable to stable regions, represented by fluctuation energy flux${\varGamma _\varXi } = {V_r}\ast {(\tilde{p})^2}$![]() . However, it has been observed in previous BOUT++ simulations that small ELMs can also be triggered by the local SOL instability with steep SOL profiles (Li et al. Reference Li, Xu, Wang, Lin, Yan and Xu2022a). To ensure a fair comparison and gain an understanding of the impact of this local instability on edge plasma dynamics, particularly associated with ELM size and SOL width, a local ballooning mode in the SOL is artificially excited by steepening the pressure profile in the SOL, as illustrated in the simulations for small ELM with shot #103745. To achieve this, we modify the density profile in the SOL while maintaining the same temperature profile to obtain the desired steep SOL pressure profile. This approach enables us to place the two physical phenomena on equal footing and provide deeper insights into their respective effects on the edge plasma dynamics.
. However, it has been observed in previous BOUT++ simulations that small ELMs can also be triggered by the local SOL instability with steep SOL profiles (Li et al. Reference Li, Xu, Wang, Lin, Yan and Xu2022a). To ensure a fair comparison and gain an understanding of the impact of this local instability on edge plasma dynamics, particularly associated with ELM size and SOL width, a local ballooning mode in the SOL is artificially excited by steepening the pressure profile in the SOL, as illustrated in the simulations for small ELM with shot #103745. To achieve this, we modify the density profile in the SOL while maintaining the same temperature profile to obtain the desired steep SOL pressure profile. This approach enables us to place the two physical phenomena on equal footing and provide deeper insights into their respective effects on the edge plasma dynamics.
In this section, two nonlinear simulations are performed: one with flat and the other with a monotonically decreasing (steep) SOL profiles, as shown in figure 13. The pressure profile with flat SOL is depicted by the black curve, while the red curve represents the profile with a monotonically decreasing (steep) SOL. For consistency, we use the diamagnetic Er in these two cases. It is important to note that the case with flat SOL profile is the same as the Er1.0BLACK case discussed in § 4, enabling a meaningful comparison. These two simulations are performed using the same nonlinear simulations setting to ensure accuracy and fairness in the comparison.

Figure 13. Radial profile of pressure (solid) and pressure gradient (dashed) with flat SOL (black) and steep SOL profiles (red).
To investigate the impact of local instability on the generation of the turbulence at the edge, we calculate the time evolution of the pressure perturbation at different radial locations. Figure 14 shows the time evolution of the root-mean-square (r.m.s.) value of the pressure perturbation at the outer midplane, both at the location of peak gradient of pressure in figure 14(a) and at the separatrix in figure 14(b). In the linear phase, the dominant mode inside the pedestal, located at the peak pressure gradient for two cases, is driven by the ideal peeling-ballooning mode. Consequently, the pressure fluctuation levels are comparable between the two cases at this location. Near the separatrix, during the early nonlinear phase, the fluctuation levels are also comparable due to similar turbulent transport from the pedestal to the SOL. A small ELM is triggered with similar linear growth rate, resulting in comparable ELM size for two cases during this phase, as shown in figure 15(b). However, during the later nonlinear phase, a stronger pressure fluctuation is generated by the local SOL instability, specifically the ballooning mode induced by the steep SOL pressure gradient, as shown by figure 14(b). This enhanced radial turbulence transport leads to a large pedestal crash, resulting in increased pedestal energy loss during this later nonlinear phase, as show in figure 15(b).

Figure 14. Time evolution of r.m.s. part of pressure at OMP for cases with flat SOL (black) and steep SOL profile (red): (a) at peak gradient location with ${\psi _n}\sim 0.93$![]() and (b) at separatrix.
and (b) at separatrix.

Figure 15. (a) Normalized pressure fluctuation intensity at outer midplane in the linear (solid) and the nonlinear phase (dashed); (b) time evolution of 3-D relative ELM size for cases with flat SOL (black) and steep SOL pressure profile (red).
As mentioned earlier, small ELMs can be triggered by a local instability at the pedestal bottom (Li et al. Reference Li, Xu, Wang, Lin, Yan and Xu2022a). The presence of a steep SOL pressure gradient drives a local ballooning instability in the SOL, leading to enhanced turbulence spreading. Now, we aim to explore how these local SOL profiles affect the inward spreading and the associated ELM size. For this analysis, we calculate the p.d.f.s of the normalized pressure fluctuation $\tilde{p}/{p_{\textrm{ped}}}$![]() and fluctuation energy flux ${\varGamma _\varXi } = {V_r}\ast {(\tilde{p})^2}$
and fluctuation energy flux ${\varGamma _\varXi } = {V_r}\ast {(\tilde{p})^2}$![]() at the pedestal bottom during the nonlinear phase, as shown in figure 16. With the steep SOL profile, the p.d.f.s shift towards higher magnitude of pressure fluctuation, indicating a large outward spreading compared to the case with the flat SOL profile, as shown by figure 16(a). This finding is consistent with the r.m.s. part of the pressure near the separatrix, as shown in figure 14(b). Moreover, the p.d.f.s of fluctuation energy flux ${\varGamma _\varXi } = {V_r}\ast {(\tilde{p})^2}$
at the pedestal bottom during the nonlinear phase, as shown in figure 16. With the steep SOL profile, the p.d.f.s shift towards higher magnitude of pressure fluctuation, indicating a large outward spreading compared to the case with the flat SOL profile, as shown by figure 16(a). This finding is consistent with the r.m.s. part of the pressure near the separatrix, as shown in figure 14(b). Moreover, the p.d.f.s of fluctuation energy flux ${\varGamma _\varXi } = {V_r}\ast {(\tilde{p})^2}$![]() show that the steep SOL profiles promote enhanced inward and outward spreading, as shown in figure 16(b). Positive values represent outward energy flux transport, while negative values denote inward energy flux. With the transition from the flat SOL (black curve) to the steep SOL (red curve), the probability of the high-amplitude fluctuation energy flux events increases for both positive and negative energy flux. Consequently, both inward and outward spreading are enhanced by the steep SOL profile, leading to a larger inward penetration depth, as shown in figure 15(a). Here the solid curve represents the radial profile of normalized pressure fluctuation intensity at the outer midplane in the linear phase, while the dashed curves correspond to the nonlinear phase.
show that the steep SOL profiles promote enhanced inward and outward spreading, as shown in figure 16(b). Positive values represent outward energy flux transport, while negative values denote inward energy flux. With the transition from the flat SOL (black curve) to the steep SOL (red curve), the probability of the high-amplitude fluctuation energy flux events increases for both positive and negative energy flux. Consequently, both inward and outward spreading are enhanced by the steep SOL profile, leading to a larger inward penetration depth, as shown in figure 15(a). Here the solid curve represents the radial profile of normalized pressure fluctuation intensity at the outer midplane in the linear phase, while the dashed curves correspond to the nonlinear phase.

Figure 16. Probability distribution functions of (a) normalized pressure fluctuation $\tilde{p}/{p_{\textrm{ped}}}$![]() and (b) energy flux ${V_r}\ast {(\tilde{p})^2}$
and (b) energy flux ${V_r}\ast {(\tilde{p})^2}$![]() at pedestal bottom with ${\psi _n} = 0.99$
at pedestal bottom with ${\psi _n} = 0.99$![]() for cases with flat SOL (black) and steep SOL profile (red).
for cases with flat SOL (black) and steep SOL profile (red).
In the presence of the steep SOL profile, the inward mixing penetration broadens, resulting in a larger ELM size, as shown in figure 15(b). Additionally, the enhanced outward turbulence spreading due to the local instability can broaden the divertor heat flux width. Further details regarding the outward turbulence spreading versus the SOL width will be discussed in § 6.
6. Impact of turbulence spreading on the divertor heat flux width
In the small ELM regime, a strong turbulence spreading occurs both inward and outward, in contrast to the ELM-free regime. The inward spreading leads to an increase of the ELM size, while the outward spreading facilitates strong radial turbulent transport in the SOL region, even when the SOL is locally stable. To investigate the impact of outward turbulence spreading on the divertor heat flux width, the parallel heat flux is calculated on the outer divertor target for different Er and SOL profiles, as described in §§ 4 and 5. The heat flux width is calculated using the Eich fitting formula (Eich et al. Reference Eich, Sieglin, Scarabosio, Fundamenski, Goldston and Herrmann2011; Reference Eich2013), represented by the expression:

and $\bar{s} = (R - {R_{\textrm{sep}}}) \cdot {f_x}$![]() . Here R is the major radius with ${R_{\textrm{sep}}}$
. Here R is the major radius with ${R_{\textrm{sep}}}$![]() denoting the separatrix position at the outer midplane and ${f_x}$
denoting the separatrix position at the outer midplane and ${f_x}$![]() is the effective magnetic flux expansion from the outer midplane to the divertor. Using this fitting formula, the width ${\lambda _q}$
is the effective magnetic flux expansion from the outer midplane to the divertor. Using this fitting formula, the width ${\lambda _q}$![]() and the divertor power spreading parameter S can be obtained. Figure 17 presents an example of the fitting for the BOUT++ simulations data for the small ELM case with shot #103745 (Er1.0BLACK in § 4.1). The black points show the BOUT++ simulation data for the parallel heat flux on the outer divertor target with the diamagnetic $E_r^{\textrm{dia}}$
and the divertor power spreading parameter S can be obtained. Figure 17 presents an example of the fitting for the BOUT++ simulations data for the small ELM case with shot #103745 (Er1.0BLACK in § 4.1). The black points show the BOUT++ simulation data for the parallel heat flux on the outer divertor target with the diamagnetic $E_r^{\textrm{dia}}$![]() . The red curve represents the fit to the simulation data using the fitting formula with $\lambda _q^{\textrm{fit}} = 3.24\ \textrm{mm}$
. The red curve represents the fit to the simulation data using the fitting formula with $\lambda _q^{\textrm{fit}} = 3.24\ \textrm{mm}$![]() and $S = 1.85\ \textrm{mm}$
and $S = 1.85\ \textrm{mm}$![]() . To account for the larger spreading factor S dominating over ${\lambda _q}$
. To account for the larger spreading factor S dominating over ${\lambda _q}$![]() , we use the integral power decay length ${\lambda _{\textrm{int}}}$
, we use the integral power decay length ${\lambda _{\textrm{int}}}$![]() in the paper (Eich et al. Reference Eich, Sieglin, Scarabosio, Fundamenski, Goldston and Herrmann2011). For this small ELM case, the integral power decay length is ${\lambda _{\textrm{int}}} = 6.27\ \textrm{mm}$
in the paper (Eich et al. Reference Eich, Sieglin, Scarabosio, Fundamenski, Goldston and Herrmann2011). For this small ELM case, the integral power decay length is ${\lambda _{\textrm{int}}} = 6.27\ \textrm{mm}$![]() . The integral power decay length ${\lambda _{\textrm{int}}}$
. The integral power decay length ${\lambda _{\textrm{int}}}$![]() is significantly larger than ${\lambda _q}$
is significantly larger than ${\lambda _q}$![]() due to the peak heat flux location shifts outward from separatrix with small ELMs. The ITPA multi-machine scaling law provides $\lambda _q^{\textrm{Eich}}\sim 4.08\ \textrm{mm}$
due to the peak heat flux location shifts outward from separatrix with small ELMs. The ITPA multi-machine scaling law provides $\lambda _q^{\textrm{Eich}}\sim 4.08\ \textrm{mm}$![]() calculated by the formula (Eich et al. Reference Eich, Sieglin, Scarabosio, Fundamenski, Goldston and Herrmann2011) $\lambda _q^{\textrm{Eich}} = 0.63 \times B_{\textrm{pol,MP}}^{ - 1.19}$
calculated by the formula (Eich et al. Reference Eich, Sieglin, Scarabosio, Fundamenski, Goldston and Herrmann2011) $\lambda _q^{\textrm{Eich}} = 0.63 \times B_{\textrm{pol,MP}}^{ - 1.19}$![]() . The width calculated by Goldston heuristic drift (HD) model with the formula (Goldston Reference Goldston2012) $\lambda _q^{\textrm{HD}} = (4a/\bar{Z}e{B_p}R){(\bar{A}{m_p}{T_{\textrm{sep}}}/(1 + \bar{Z}))^{1/2}}$
. The width calculated by Goldston heuristic drift (HD) model with the formula (Goldston Reference Goldston2012) $\lambda _q^{\textrm{HD}} = (4a/\bar{Z}e{B_p}R){(\bar{A}{m_p}{T_{\textrm{sep}}}/(1 + \bar{Z}))^{1/2}}$![]() is $\lambda _q^{\textrm{HD}}\sim 6.90\ \textrm{mm}$
is $\lambda _q^{\textrm{HD}}\sim 6.90\ \textrm{mm}$![]() . Here ${B_p}$
. Here ${B_p}$![]() is the poloidally averaged value of poloidal magnetic field near the separatrix. Since the simulation and ITPA scaling law results are mapped to the outer midplane, the HD model gives $\lambda _q^{\textrm{HD}\ast }\sim 3.68\ \textrm{mm}$
is the poloidally averaged value of poloidal magnetic field near the separatrix. Since the simulation and ITPA scaling law results are mapped to the outer midplane, the HD model gives $\lambda _q^{\textrm{HD}\ast }\sim 3.68\ \textrm{mm}$![]() mapping to the outer midplane. The integral power decay length ${\lambda _{\textrm{int}}}$
mapping to the outer midplane. The integral power decay length ${\lambda _{\textrm{int}}}$![]() from BOUT++ simulation is larger than the predictions of $\lambda _q^{\textrm{Eich}}$
from BOUT++ simulation is larger than the predictions of $\lambda _q^{\textrm{Eich}}$![]() and $\lambda _q^{\mathrm{HD\ast }}$
and $\lambda _q^{\mathrm{HD\ast }}$![]() due to large radial turbulent transport with small ELMs. Notably, in BOUT++ turbulence simulation, we just simulate the ELM crash process, but not the profile recovery process. There are no ELM cycles. However, for the small ELMs, the variation of peak heat flux is <50 % with quasi-continuous power exhaust to the divertors and high ELM frequency. The heat flux width calculated based on the peak heat flux time point is close to the average over multiple ELM cycles for small ELMs.
due to large radial turbulent transport with small ELMs. Notably, in BOUT++ turbulence simulation, we just simulate the ELM crash process, but not the profile recovery process. There are no ELM cycles. However, for the small ELMs, the variation of peak heat flux is <50 % with quasi-continuous power exhaust to the divertors and high ELM frequency. The heat flux width calculated based on the peak heat flux time point is close to the average over multiple ELM cycles for small ELMs.

Figure 17. Parallel heat flux on the outer divertor with the diamagnetic Er for shot #103745; the black points are from BOUT++ simulations and the red curve is a fit to the profile using the Eich fitting formula (Eich et al. Reference Eich, Sieglin, Scarabosio, Fundamenski, Goldston and Herrmann2011).
To investigate the relation between the turbulence spreading and divertor heat flux width, we conducted a series of simulations with different levels of the edge fluctuation by varying the radial electric field and SOL profile, as discussed in the previous sections. The spatio-temporal evolution of the fluctuation intensity ${(\tilde{p}/{p_0})^2}$![]() at the LCFS serves a good indicator of turbulence spreading. As demonstrated in § 4.1, a deeper Er well leads to the increased pedestal energy loss, resulting in stronger energy transport from the pedestal to the SOL. Figure 18 shows the time evolution the fluctuation intensity ${(\tilde{p}/{p_0})^2}$
at the LCFS serves a good indicator of turbulence spreading. As demonstrated in § 4.1, a deeper Er well leads to the increased pedestal energy loss, resulting in stronger energy transport from the pedestal to the SOL. Figure 18 shows the time evolution the fluctuation intensity ${(\tilde{p}/{p_0})^2}$![]() at the LCFS of the outer midplane for different cases: Er1.0BLACK (black curve), Er1.5RED (red curve), Er2.0BLUE (blue curve) and Er2.5GREEN (green curve). As the Er well deepens, the fluctuation intensity at the LCFs increases, and the time-averaged fluctuation level during the nonlinear phase also increases. For cases with small ELMs (Er1.0BLACK, Er1.5RED, Er2.0BLUE), the fluctuation level is much smaller than in the case with large ELMs (Er2.5GREEN) due to the larger pedestal crash experienced in the latter. In summary, the analysis of the fluctuation intensity at the LCFS help us better understand the relationship between turbulence spreading and the divertor heat flux width ${\lambda _q}$
at the LCFS of the outer midplane for different cases: Er1.0BLACK (black curve), Er1.5RED (red curve), Er2.0BLUE (blue curve) and Er2.5GREEN (green curve). As the Er well deepens, the fluctuation intensity at the LCFs increases, and the time-averaged fluctuation level during the nonlinear phase also increases. For cases with small ELMs (Er1.0BLACK, Er1.5RED, Er2.0BLUE), the fluctuation level is much smaller than in the case with large ELMs (Er2.5GREEN) due to the larger pedestal crash experienced in the latter. In summary, the analysis of the fluctuation intensity at the LCFS help us better understand the relationship between turbulence spreading and the divertor heat flux width ${\lambda _q}$![]() , showing that a deeper Er well will lead to enhanced turbulence spreading and higher fluctuation levels. Additionally, small ELM cases exhibit significantly lower fluctuation levels compared with large ELM cases due to differences in the pedestal crash behaviour.
, showing that a deeper Er well will lead to enhanced turbulence spreading and higher fluctuation levels. Additionally, small ELM cases exhibit significantly lower fluctuation levels compared with large ELM cases due to differences in the pedestal crash behaviour.

Figure 18. Time evolution of fluctuation intensity ${(\tilde{p}/{p_0})^2}$![]() at outer midplane near the separatrix with different radial electric field profile.
at outer midplane near the separatrix with different radial electric field profile.
As we mentioned in the previous section, the extent of both inward and outward turbulence spreading is heavily influenced by the magnitude of fluctuation energy flux. To investigate the correlation between turbulence spreading and divertor heat flux width, we introduce the fluctuation energy density flux ${\varGamma _\varepsilon } = c_s^2\widetilde {{V_r}}{(\tilde{p}/{p_0})^2}$![]() at the last closed flux surface. This measurement quantifies the turbulence spreading from the pedestal to the SOL. Here ${c_s}$
at the last closed flux surface. This measurement quantifies the turbulence spreading from the pedestal to the SOL. Here ${c_s}$![]() represents the sound speed and $\widetilde {{V_r}}$
represents the sound speed and $\widetilde {{V_r}}$![]() denotes the fluctuation in radial velocity. In the pedestal Er scan, an increase in E × B flow results in a corresponding rise in edge fluctuation energy intensity flux, leading to a broadening of the divertor heat flux width, as shown by the data points in figure 19. The black, red and blue points represent small ELM, while the green point corresponds to a large ELM. The dashed black horizontal line represents the width based on the ITPA multi-machine scaling law. Consequently, as we transition from ELM-free to small and then to larger ELMs, the divertor heat flux width experiences significant broadening due to strong radial turbulence spreading from the pedestal to the SOL. Notably, DIII-D experiments using Resonant Magnetic Perturbations (RMPs) 3-D fields have also demonstrated that, from the inter-ELM phase to the grassy ELM phase (achieved by increasing RMP current), the width on the inner divertor target increases approximately two times with low RMP current and approximately four times with high RMP current. However, it is important to note that the peak divertor heat flux is much smaller compared to the case of type-I ELMs (Nazikian et al. Reference Nazikian2018; Xu Reference Xu2020). Nevertheless, due to the diagnostic limitations, further investigation is required to establish the relationship between turbulence and heat flux width from experimental data. In our simulations, we employ the heat flux profile at the end of a simulation to estimate the width for the large ELM.
denotes the fluctuation in radial velocity. In the pedestal Er scan, an increase in E × B flow results in a corresponding rise in edge fluctuation energy intensity flux, leading to a broadening of the divertor heat flux width, as shown by the data points in figure 19. The black, red and blue points represent small ELM, while the green point corresponds to a large ELM. The dashed black horizontal line represents the width based on the ITPA multi-machine scaling law. Consequently, as we transition from ELM-free to small and then to larger ELMs, the divertor heat flux width experiences significant broadening due to strong radial turbulence spreading from the pedestal to the SOL. Notably, DIII-D experiments using Resonant Magnetic Perturbations (RMPs) 3-D fields have also demonstrated that, from the inter-ELM phase to the grassy ELM phase (achieved by increasing RMP current), the width on the inner divertor target increases approximately two times with low RMP current and approximately four times with high RMP current. However, it is important to note that the peak divertor heat flux is much smaller compared to the case of type-I ELMs (Nazikian et al. Reference Nazikian2018; Xu Reference Xu2020). Nevertheless, due to the diagnostic limitations, further investigation is required to establish the relationship between turbulence and heat flux width from experimental data. In our simulations, we employ the heat flux profile at the end of a simulation to estimate the width for the large ELM.

Figure 19. Divertor heat flux width ${\lambda _{\textrm{int}}}$![]() versus fluctuation energy intensity flux ${\varGamma _\varepsilon }$
versus fluctuation energy intensity flux ${\varGamma _\varepsilon }$![]() .
.
Despite the significant broadening of heat flux width observed from small ELMs to large ELMs, it is essential to acknowledge that the pedestal relaxation is much stronger for large ELMs, resulting in a larger ELM size and higher peak heat flux. However, due to the large energy loss from pedestal to SOL for large ELMs, the peak heat flux deposited on the divertor is considerably larger compared to small ELMs, exceeding it by more than one order of magnitude. This possess a concern, particularly for ITER (Loarte et al. Reference Loarte2007; Eich et al. Reference Eich, Sieglin, Thornton, Faitsch, Kirk, Herrmann and Suttrop2017), where such high heat flux with large ELMs is not tolerable for the materials, such as carbon and tungsten. However, for small ELMs, the ELM size is significantly smaller compared to that of large ELMs, yet allowing the heat flux width to be broadened with a decreasing peak heat flux. From the pedestal Er scan, as discussed in § 4.1, it demonstrates that ${\lambda _{\textrm{int}}}$![]() can be broadened up to 3× larger (blue point) than predicted by the multi-machine scaling law (dashed line in figure 19) and HD model with small ELMs. Here it should be noted that the comparison between ${\lambda _{\textrm{int}}}$
can be broadened up to 3× larger (blue point) than predicted by the multi-machine scaling law (dashed line in figure 19) and HD model with small ELMs. Here it should be noted that the comparison between ${\lambda _{\textrm{int}}}$![]() and ${\lambda _q}$
and ${\lambda _q}$![]() from ITPA scaling law may be not exactly equal. The integral power decay length ${\lambda _{\textrm{int}}}$
from ITPA scaling law may be not exactly equal. The integral power decay length ${\lambda _{\textrm{int}}}$![]() in experimental devices is significantly larger than ${\lambda _q}$
in experimental devices is significantly larger than ${\lambda _q}$![]() as the peak heat flux location shifts outward, which is related to the S parameter. Further investigation with the S effect is more relevant.
as the peak heat flux location shifts outward, which is related to the S parameter. Further investigation with the S effect is more relevant.
When comparing the impact of pedestal Er on the divertor heat flux width with the effect of local SOL Er shear, we observe a suppressing effect on the heat flux width. The divertor heat flux width decreases with strong local SOL E × B shear, as indicated by the stars in figure 19. The black star represents a case with small SOL E × B shear, while the red star corresponds to the case with strong SOL E × B shear. Two mechanisms are at play to reduce the heat flux width with strong local SOL E × B shear: (1) the E × B shear in the SOL suppresses turbulence spreading in that region, leading to reduced radial transport; (2) the strong SOL Er increases the parallel velocity induced by the E × B drift and reduces the parallel transport time, thus enhancing the parallel transport (Li et al. Reference Li, Xu, Goldston, Sun and Wang2021). Additionally, as discussed in § 5, the local SOL instability can enhance outward turbulence spreading by increasing the SOL pressure gradient. The divertor heat flux width ${\lambda _{\textrm{int}}}$![]() and fluctuation energy intensity flux ${\varGamma _\varepsilon }$
and fluctuation energy intensity flux ${\varGamma _\varepsilon }$![]() with a steep SOL profile is also calculated, as shown by the red circle in figure 19. With a steep SOL profile, the fluctuation energy intensity flux increases, consequently broadening the heat flux width.
with a steep SOL profile is also calculated, as shown by the red circle in figure 19. With a steep SOL profile, the fluctuation energy intensity flux increases, consequently broadening the heat flux width.
In table 1, we summarize the main results of our study. Both the Er profiles and SOL profiles are found to play crucial roles in both inward and outward turbulence spreading in H-mode with small/grassy ELMs. Notably, the increase in inward spreading leads to a larger ELM size, while outward spreading can broaden the SOL width. These findings are consistent with the theory of turbulence spreading (Chu, Diamonds & Guo Reference Chu, Diamonds and Guo2022). Figure 19 provides a comprehensive overview of the divertor heat flux width ${\lambda _{\textrm{int}}}$![]() plotted against the fluctuation energy intensity flux ${\varGamma _\varepsilon }$
plotted against the fluctuation energy intensity flux ${\varGamma _\varepsilon }$![]() for all the cases discussed in this paper. The results show that as the edge fluctuation energy intensity flux increases, the heat flux width can be significantly broadened. Particularly, in the small ELM regime, control of edge fluctuations, such as increasing pedestal E × B net flow, decreasing local SOL E × B shear or enhancing local SOL turbulence by steep SOL profiles, can lead to significant broadening of the divertor heat flux width ${\lambda _{\textrm{int}}}$
for all the cases discussed in this paper. The results show that as the edge fluctuation energy intensity flux increases, the heat flux width can be significantly broadened. Particularly, in the small ELM regime, control of edge fluctuations, such as increasing pedestal E × B net flow, decreasing local SOL E × B shear or enhancing local SOL turbulence by steep SOL profiles, can lead to significant broadening of the divertor heat flux width ${\lambda _{\textrm{int}}}$![]() . These findings offer promising possibilities for controlling and optimizing heat flux distribution in fusion reactors with both high confinement operations and tolerable divertor exhaust.
. These findings offer promising possibilities for controlling and optimizing heat flux distribution in fusion reactors with both high confinement operations and tolerable divertor exhaust.
Table 1. Radial electric field and local SOL instability effects on the ELM size and SOL width ${\lambda _q}$![]() .
.

7. Summary and discussion
We conduct BOUT++ six-field two-fluid turbulence simulations to investigate the effects of turbulence spreading on the ELM size and the divertor heat flux width. The simulations focus on EAST discharges with small ELMs, specifically shot#103745 and shot #090949, and their evolution by varying the pedestal Er, the SOL Er and SOL profiles. The BOUT++ simulations show that the Er profile and local SOL instability significantly influence the edge turbulence spreading and divertor heat flux width. To study the impact of Er on the edge plasma dynamics, we perform a pedestal Er scan for shot #103745 by multiplying the diamagnetic $E_r^{\textrm{dia}}$![]() by factors 1.0×, 1.5×, 2×, 2.5× while keeping the pressure profile fixed (§ 4.1). Essentially, the Er scan is equivalent to the plasma flow $\boldsymbol{V}$
by factors 1.0×, 1.5×, 2×, 2.5× while keeping the pressure profile fixed (§ 4.1). Essentially, the Er scan is equivalent to the plasma flow $\boldsymbol{V}$![]() or $E_r^{V \times B}$
or $E_r^{V \times B}$![]() scan with specific flow profiles, generating the same profiles as the diamagnetic Er, but with varying magnitudes. For investigating the local SOL E × B shear effects on SOL turbulence and divertor heat flux, we self-consistently simulate the edge Er using the BOUT++ transport module in a radial domain across the separatrix and with sheath boundary conditions on the divertor plates for shot #090949 (§ 4.2). Additionally, we study the impact of the local SOL instability on both inward and outward turbulence spreading by steepening the SOL pressure profile for shot #103745 (§ 5). These comprehensive simulations shed light on the physics mechanisms controlling turbulence spreading and divertor heat flux, providing valuable insights for fusion plasma research and reactor design.
scan with specific flow profiles, generating the same profiles as the diamagnetic Er, but with varying magnitudes. For investigating the local SOL E × B shear effects on SOL turbulence and divertor heat flux, we self-consistently simulate the edge Er using the BOUT++ transport module in a radial domain across the separatrix and with sheath boundary conditions on the divertor plates for shot #090949 (§ 4.2). Additionally, we study the impact of the local SOL instability on both inward and outward turbulence spreading by steepening the SOL pressure profile for shot #103745 (§ 5). These comprehensive simulations shed light on the physics mechanisms controlling turbulence spreading and divertor heat flux, providing valuable insights for fusion plasma research and reactor design.
In BOUT++ linear simulations, we conduct a pedestal Er scan for small ELMs (shot #103745) and observe the following trends. As the pedestal Er well deepens, the high-n ballooning modes become stabilized, while the low-n peeling mode is destabilized. This shifts the dominant modes from high-n to low-n modes with a narrow mode spectrum and the maximum linear growth rate increases. Moving to the nonlinear simulations, we find that the fluctuation level increases, as the Er well deepens, leading to an increased inward penetration toward the pedestal top and, consequently, an increased ELM size. However, these three cases remain within the small ELM regime, as no front propagation occurs. In the small ELMs, the pedestal relaxes into a linearly stable profile after the initial ELM crash. In contrast, when the Er is further increased, such as in the case Er2.5GREEN, the fluctuation level significantly increases and the profile steepening shifts inward after the initial ELM crash at the peak pressure gradient position. As a result, the linear instability zone shifts inward, leading to a second pedestal crash. This continuous pressure profile crashing extends up to the pedestal top, triggering fast front propagation and deep inward penetration. We term this phenomenon an ‘avalanche process’, characterized by a rapid front propagation and the occurrence of the large ELMs. Therefore, the transition from small to large ELMs occurs by increasing inward turbulence spreading with the increasing pedestal E × B net flow. Additionally, the outward SOL spreading is enhanced due to the increased fluctuation level and turbulent transport from the pedestal to the SOL. In summary, the pedestal Er scan reveals the following characteristics of turbulence spreading for ELMs.
(1) For the large ELMs, the pedestal exhibits remarkable instability with a high linear growth rate. This leads to a strong avalanche process during the nonlinear phase, characterized by a robust inward penetration of the mixing zone. Consequently, the ELM size becomes significantly large, often with $\Delta {W_{\textrm{ped}}}/{W_{\textrm{ped}}} \gg 1\,\%$
 .
.(2) For the small ELMs, the pedestal approaches a state of near marginal stability. Following the initial ELM crash, the pedestal relaxes into a state of linear stability. While a distinct front propagation might not be evident, a prominent inward penetration is still observed. The ELM size is much smaller than that of the large ELMs. It is worth noting that the regime of ‘near marginal stability’ holds crucial significance here.
As the pedestal E × B shear flow increases, an intriguing pattern emerges: the high-n ballooning modes experience stabilization, while the low-n peeling modes undergo destabilization. This dual effect leads to an increase in the maximum linear growth rate and a narrowing of the mode spectrum. The process of enhanced inward turbulence spreading is triggered by increasing pedestal Er. Remarkably, even within the small ELM regime, augmenting the inward penetration depth can lead to an increase in the ELM size. It is worth noting that the Er scan performed in this study holds equivalence to the plasma flow $\boldsymbol{V}$![]() scan, characterized by specific flow profiles that generate the same profiles as the diamagnetic Er, albeit with varying magnitudes. The practical implementation of this approach within an experimental setting necessitates further investigation.
scan, characterized by specific flow profiles that generate the same profiles as the diamagnetic Er, albeit with varying magnitudes. The practical implementation of this approach within an experimental setting necessitates further investigation.
(3) In the course of ELM events, both strong inward and outward spreading phenomena are observed. The ELM size strongly depends on the extent of inward spreading. Within the small ELM regime, the ELM size exhibits an almost linear correlation with the depth of inward penetration. Moreover, the outward spreading amplifies the levels of fluctuation and the energy intensity flux ${\varGamma _\varepsilon }$
 at the LCFS, thereby enhancing turbulence transport from the pedestal to the SOL. This augmentation can lead to a broadening of the SOL width by approximately three times, in comparison to the ITPA multi-machine scaling law, prominently driven by strong outward turbulence spreading.
at the LCFS, thereby enhancing turbulence transport from the pedestal to the SOL. This augmentation can lead to a broadening of the SOL width by approximately three times, in comparison to the ITPA multi-machine scaling law, prominently driven by strong outward turbulence spreading.
Furthermore, within the scope of this paper, an exploration of the impact of local SOL E × B shear and local SOL instability on turbulence spreading is undertaken. To attain a more realistic Er profile that encompasses SOL physics, accounting for sheath boundary effects, the BOUT++ transport module is used to self-consistently simulate the Er profile. Through comparisons with SOL E × B shear and those excluding it, it is evident that local SOL E × B shear has a strong effect on the outward SOL turbulence spreading. This influence leads to a suppression of outward SOL turbulence spreading when a substantial local SOL E × B shear is present. BOUT++ nonlinear simulations are employed to investigate the effects of both flat and steep SOL profiles. These simulations reveal that local SOL instability is capable of driving both strong inward and outward turbulence spreading. Particularly under a steep SOL profile, a substantial inward energy flux is induced, leading to a heightened level of inward turbulence spreading. This augmentation subsequently contributes to an escalation in the size of ELMs.
In our BOUT++ simulations, we examined the behaviour of the divertor heat flux width ${\lambda _q}$![]() , revealing its close association with the outward spread of edge fluctuation from the pedestal to the SOL within the small ELM regime. Notably, the increase in the divertor heat flux width ${\lambda _q}$
, revealing its close association with the outward spread of edge fluctuation from the pedestal to the SOL within the small ELM regime. Notably, the increase in the divertor heat flux width ${\lambda _q}$![]() corresponds to heightened levels of fluctuation energy intensity flux ${\varGamma _\varepsilon }$
corresponds to heightened levels of fluctuation energy intensity flux ${\varGamma _\varepsilon }$![]() at the last closed flux surface, aligning well with turbulence spreading theory. As the pedestal Er well deepens due to additional net flow (as described in § 4.1), the spreading of pedestal turbulence is amplified. This enhanced transport from the pedestal to the SOL propels an increase in ${\varGamma _\varepsilon }$
at the last closed flux surface, aligning well with turbulence spreading theory. As the pedestal Er well deepens due to additional net flow (as described in § 4.1), the spreading of pedestal turbulence is amplified. This enhanced transport from the pedestal to the SOL propels an increase in ${\varGamma _\varepsilon }$![]() , thereby leading to a broader divertor heat flux width. However, it is important to note that the local SOL E × B shear plays a dual role. While it suppresses outward turbulence spreading, it simultaneously enhances the parallel transport within the SOL, resulting in a reduced heat flux width. Furthermore, the local SOL turbulence contributes to both inward and outward turbulence spreading, thereby leading to an increased fluctuation energy intensity flux ${\varGamma _\varepsilon }$
, thereby leading to a broader divertor heat flux width. However, it is important to note that the local SOL E × B shear plays a dual role. While it suppresses outward turbulence spreading, it simultaneously enhances the parallel transport within the SOL, resulting in a reduced heat flux width. Furthermore, the local SOL turbulence contributes to both inward and outward turbulence spreading, thereby leading to an increased fluctuation energy intensity flux ${\varGamma _\varepsilon }$![]() . Overall, the divertor heat flux width ${\lambda _q}$
. Overall, the divertor heat flux width ${\lambda _q}$![]() undergoes significant broadening within small ELM regimes, as compared to the ELM-free regime, largely attributed to the strong radial turbulent transport. As the ELM size increases, the heat flux width increases. These are consistent with the experimental evidence of an increased ELM wetted area with ELM size (Eich et al. Reference Eich, Sieglin, Scarabosio, Fundamenski, Goldston and Herrmann2011, Reference Eich, Sieglin, Thornton, Faitsch, Kirk, Herrmann and Suttrop2017).
undergoes significant broadening within small ELM regimes, as compared to the ELM-free regime, largely attributed to the strong radial turbulent transport. As the ELM size increases, the heat flux width increases. These are consistent with the experimental evidence of an increased ELM wetted area with ELM size (Eich et al. Reference Eich, Sieglin, Scarabosio, Fundamenski, Goldston and Herrmann2011, Reference Eich, Sieglin, Thornton, Faitsch, Kirk, Herrmann and Suttrop2017).
This paper focuses on the simulation results concerning the characteristic of pedestal turbulence spreading within the ELM regimes and its impact on both ELM size and heat flux width. In pursuit of a more compressive understanding, additional comparisons with experimental data warrant deeper investigation. The following issues of significance include the following.
(1) The Er scan indicates that raising the pedestal Er profile can significantly amplify pedestal instability, and the reduction of SOL Er is linked to the broadening of the heat flux width. This suggests a potential pathway to transition into the small ELM regime through controlled adjustments of the Er profile, possibly achieved by controlling toroidal rotation. Nevertheless, the question is: Can this conceptual approach feasibly translate into experimental implementation?
(2) The size of ELMs finds its roots in the depth of inward turbulence spreading, closely linked to the area affected by the ELM, as discussed in experimental measurements. Further exploration through studies of avalanche and turbulence spreading could offer valuable insights into precisely determining the extent of the ELM-affected area and subsequently building strategies for ELM control. Further research is needed to control and predict these factors in experiments.
(3) The fluctuation energy intensity flux ${\varGamma _\varepsilon }$
 is a critical parameter, effectively bridging the gap between pedestal physics and divertor heat flux width ${\lambda _q}$
is a critical parameter, effectively bridging the gap between pedestal physics and divertor heat flux width ${\lambda _q}$ within the small ELM regime. It is noteworthy that ${\lambda _q}$
within the small ELM regime. It is noteworthy that ${\lambda _q}$ increases correspondingly with an increase in fluctuation energy intensity flux ${\varGamma _\varepsilon }$
increases correspondingly with an increase in fluctuation energy intensity flux ${\varGamma _\varepsilon }$ at the LCFs. This relationship presents an opportunity for experimental measurement. However, the precise value of the optimal ${\varGamma _\varepsilon }$
at the LCFs. This relationship presents an opportunity for experimental measurement. However, the precise value of the optimal ${\varGamma _\varepsilon }$ in the small ELM regime remains undetermined.
in the small ELM regime remains undetermined.
In conclusion, the potential of operating in H-mode with small ELMs offers a promising avenue for addressing two critical challenges: the reduction of ELM size and the expansion of the SOL width. However, the pathway to effectively controlling the parameters required to access this promising regime in experimental settings necessitates dedicated further research endeavours.
Acknowledgements
The authors thank Dr Z. Li, Dr H. Wang, Dr Q. Yang, and the BOUT++ team and the EAST experimental team for valuable discussions. This research used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231.
Editor Paolo Ricci thanks the referees for their advice in evaluating this article.
Declaration of interests
The authors report no conflict of interest.
Funding
This work was performed under the U.S. Department of Energy by Lawrence Livermore National Laboratory under Contract No. DE-AC52-07NA27344, LLNL-JRNL-843534 and by UCSD under Contract No. DE-FG02-04ER54738. This work also was supported by the SciDAC ABOUND Project, SCW1832 and by the Users with Excellence Program of Hefei Science Center, CAS under grant Nos. 2021HSC-UE014.