1. Introduction
The SPARC tokamak (Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020) is being designed to demonstrate significant fusion gain (Q > 2) for the first time, using a modestly sized device with high magnetic field enabled by recent advances in high-temperature superconductor technology. The basic parameters needed to achieve the performance goals of SPARC can be estimated using zero-dimensional (0D) analysis based on empirical confinement scalings, with increasing confidence provided by full 1.5D transport simulations, grounded in validated physics models (Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020). Results of these efforts have a strong sensitivity to particular inputs. In the former case, the assumed H-factor is a significant lever on the Q projected for SPARC. In the latter case, performance is varied in practice by the choice of pedestal boundary condition, i.e. plasma density and temperature at a normalized minor radius r/a of perhaps 0.9–0.95. Given these boundary conditions, the plasma H-factor is determined self-consistently by evaluation of turbulent and neoclassical fluxes in the core. Owing to the stiff nature of the core transport in high-performance plasma conditions, the H-factor is strongly dependent on the pedestal boundary condition (Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020). The link between pedestal quality and H-factor is well established in existing experiments, for example in Hughes et al. (Reference Hughes, Loarte, Reinke, Terry, Brunner, Greenwald, Hubbard, LaBombard, Lipschultz and Ma2011) and Leyland et al. (Reference Leyland, Beurskens, Frassinetti, Giroud, Saarelma, Snyder, Flanagan, Jachmich, Kempenaars and Lomas2015).
A high-quality pedestal also connects to some less-desirable features in high-energy-density tokamaks. Higher plasma pressure has been correlated with narrower scrape-off layer heat flux widths (Brunner et al. Reference Brunner, LaBombard, Kuang and Terry2018; Faitsch et al. Reference Faitsch, Eich and Sieglin2020; Silvagni et al. Reference Silvagni, Eich, Faitsch, Happel, Sieglin, David, Nille, Gil and Stroth2020), which could lead to increased challenges for divertor heat flux mitigation. In addition, high pedestal pressure is sometimes associated with large edge-localized modes (ELMs), transient phenomena that rapidly convert pedestal stored energy into bursts of energy and particles that must be borne by plasma-facing components (PFCs) in the main chamber and divertor (Leonard Reference Leonard2014).
The objective of this manuscript is to describe the methods used to make pedestal projections for SPARC, which can inform both the core performance projections and the divertor power handling requirements, as described in detail in separate papers (Kuang et al. Reference Kuang, Ballinger, Brunner, Canik, Creely, Gray, Greenwald, Hughes, Irby and LaBombard2020; Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020). The methods described all have a basis in the extensive experience of the tokamak community. We focus on empirical scalings, semi-empirical scalings and model predictions that have received extensive validation on a number of existing experiments. SPARC represents a powerful opportunity to extend the validation of these models to new regimes of tokamak operation, allowing the closing of gaps in our physics projections to pilot plant concepts.
For reference, table 1 provides key input parameters needed to evaluate the various models described in the following. These are taken from the V2 design of SPARC (Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020). Section 2 describes the assumptions used to determine H-mode access on SPARC and the outlook for pedestal formation and sustainment. Section 3 motivates EPED as the constituent model for the pedestal and discusses predictions for SPARC device designs. Section 4 discusses the implications for ELM characteristics, including transient heat loading to be addressed in divertor design, as well as effects on fusion gain that would result from ELM mitigation techniques. Conclusions and directions for future work are given in § 5.
Table 1. Full-field H-mode parameters for SPARC V2, useful as inputs to models found in the text.

2. H-mode access
2.1. Empirical scaling for H-mode power threshold
As on all tokamaks, access to a high pedestal on SPARC will require sufficient input power. In baseline high-performance operation this will enable a transition from L-mode to H-mode confinement and sustainment of the associated edge transport barrier. In the H-mode pedestal, a significant amount of mean flow shear is present to suppress turbulence, thus reducing cross-field transport and boosting confinement. Currently there is no first principles model that can deliver a general requirement for the critical flow shear, or translate flow shear into an input power requirement. Instead, the empirical approach has been pursued. L–H power threshold data from many machines have been gathered and regressed into scaling laws that can be projected, albeit imperfectly, to unbuilt devices (Ryter & H Mode Database Working Group Reference Ryter1996; Takizuka & ITPA H-mode Power Threshold Database Working Group Reference Takizuka2004; Martin, Takizuka & ITPA CDBM H-mode Threshold Database Working Group Reference Martin and Takizuka2008). The prevailing example is a power law developed from a global multimachine database and adopted by the International Tokamak Physics Activity (ITPA) (Martin et al. Reference Martin and Takizuka2008):
This scaling law was determined using actual L–H power threshold data from several tokamaks: Alcator C-Mod, ASDEX Upgrade (AUG), DIII-D, JET, JFT-2M and JT-60 U. It represents the most widely accepted empirical model for power threshold, for deuterium tokamak plasmas, operated with the ion ![]() $B \times {\bf \nabla }B$ drift directed toward a single magnetic null and at moderate to high normalized density. By way of illustration, figure 1 shows a comparison of (2.1) (blue solid curve) with experimental threshold power data from the Alcator C-Mod tokamak (Greenwald et al. Reference Greenwald, Bader, Baek, Bakhtiari, Barnard, Beck, Bergerson, Bespamyatnov, Bonoli and Brower2014). Reasonable agreement is seen between the ITPA scaling law and the data over a typical range of density at which H-mode was accessed on the device: 1–2 × 1020 m−3, with the caveat that the spread in the experimental data alone is easily a factor of two. With appropriate modifications, this scaling has been used exhaustively to project power requirements for ITER (ITER Organization, 2018), and can be applied to the design of SPARC.
$B \times {\bf \nabla }B$ drift directed toward a single magnetic null and at moderate to high normalized density. By way of illustration, figure 1 shows a comparison of (2.1) (blue solid curve) with experimental threshold power data from the Alcator C-Mod tokamak (Greenwald et al. Reference Greenwald, Bader, Baek, Bakhtiari, Barnard, Beck, Bergerson, Bespamyatnov, Bonoli and Brower2014). Reasonable agreement is seen between the ITPA scaling law and the data over a typical range of density at which H-mode was accessed on the device: 1–2 × 1020 m−3, with the caveat that the spread in the experimental data alone is easily a factor of two. With appropriate modifications, this scaling has been used exhaustively to project power requirements for ITER (ITER Organization, 2018), and can be applied to the design of SPARC.

Figure 1. C-Mod (Bt = 5.4 T) L–H threshold power versus density, both data (squares) and various model curves. The dotted purple curve is from a previous fit to C-Mod data (Ma et al. Reference Ma, Hughes, Hubbard, LaBombard, Churchill, Golfinopoulos, Tsujii and Marmar2012). The ITPA scaling law (Martin et al. Reference Martin and Takizuka2008) is plotted as a solid blue curve. A scaling based on a critical ion heat flow model for the L–H threshold (Schmidtmayr et al. Reference Schmidtmayr, Hughes, Ryter, Wolfrum, Cao, Creely, Howard, Hubbard, Lin and Reinke2018) is shown in red, with P th = 2Qi ,th. A novel low-density correction to the ITPA scaling law produces the dashed blue curve, which is important for n < n th,min as calculated according to (2.2) and illustrated by the vertical dashed line.
One important modification is needed to account for the isotope scaling of P th, because (2.1) was determined only for DD discharges. The preponderance of experience comparing L–H power thresholds in H and D plasmas indicates an isotope scaling favourable to operation in DT. One quantitative study on JET determined a scaling of P th with A −1 (Righi et al. Reference Righi, Bartlett, Christiansen, Conway, Cordey, Eriksson, De Esch, Fishpool, Gowers and de Haas1999) and other tokamaks have demonstrated isotope scalings broadly consistent with this trend (Ryter et al. Reference Ryter, Pütterich, Reich, Scarabosio, Wolfrum, Fischer, Gemisic Adamov, Hicks, Kurzan and Maggi2009, Reference Ryter, Rathgeber, Barrera Orte, Bernert, Conway, Fischer, Happel, Kurzan, McDermott and Scarabosio2013; Behn et al. Reference Behn, Labit, Karpushov, Martin and Porte2015; Yan et al. Reference Yan, Gohil, McKee, Eldon, Grierson, Rhodes and Petty2017). A linear reduction in power threshold with increasing isotope mass suggests that a 50 : 50 mix of DT would have its power threshold reduced by 20% relative to the projection from (2.1).
2.2. Low-density limit for H-mode access
Confidence in the ITPA scaling law is reduced at low density, because it was derived only with moderate- to high-density data from each device included. Neither (2.1) nor any other power law expressions for power threshold capture the tendency of a bifurcated dependence on density. Below a critical density, the power requirement takes on a negative dependence instead of positive, giving the curve a U-shape (Ryter et al. Reference Ryter, Pütterich, Reich, Scarabosio, Wolfrum, Fischer, Gemisic Adamov, Hicks, Kurzan and Maggi2009; Gohil et al. Reference Gohil, Evans, Fenstermacher, Ferron, Osborne, Park, Schmitz, Scovolle and Unterberg2011; Ma et al. Reference Ma, Hughes, Hubbard, LaBombard, Churchill, Golfinopoulos, Tsujii and Marmar2012, Maggi et al. Reference Maggi, Delabie, Biewer, Groth, Hawkes, Lehnen, de la Luna, McCormick, Reux and Rimini2014). Although the ITPA scaling law agrees well with power threshold data from C-Mod taken in a standard range of operating density, figure 1 also clearly shows the non-monotonic density dependence of P th described in detail by Ma et al. (Reference Ma, Hughes, Hubbard, LaBombard, Churchill, Golfinopoulos, Tsujii and Marmar2012). When selected subsets of this type from within the international database are analysed, the density at the bottom of the U, i.e. where power is minimized, n th,min, is seen to have a negative dependence on R and a positive dependence on BT (Martin et al. Reference Martin and Takizuka2008). The positive trend of n th,min with BT is also noted in experimental scans on individual devices (Ma et al. Reference Ma, Hughes, Hubbard, LaBombard, Churchill, Golfinopoulos, Tsujii and Marmar2012, Maggi et al. Reference Maggi, Delabie, Biewer, Groth, Hawkes, Lehnen, de la Luna, McCormick, Reux and Rimini2014).
Several models have sought to capture and explain the existence of the power threshold reversal at low density (Fundamenski et al. Reference Fundamenski, Militello, Moulton and McDonald2012; Ryter et al. Reference Ryter, Barrera Orte, Kurzan, McDermott, Tardini, Viezzer, Bernert and Fischer2014; Bourdelle et al. Reference Bourdelle, Choné, Fedorczak, Garbet, Beyer, Citrin, Delabie, Dif-Pradalier, Fuhr and Loarte2015; Malkov et al. Reference Malkov, Diamond, Miki, Rice and Tynan2015). The strength of the thermal equilibration between ions and electrons in the core plasma may be a significant player in setting the transition between the low- and high-density branch of the power threshold. Following from the hypothesis that a critical ion heat flow through the plasma edge is necessary to sustain H-mode formation, Ryter et al. (Reference Ryter, Barrera Orte, Kurzan, McDermott, Tardini, Viezzer, Bernert and Fischer2014) derived an expression for the density at minimum power threshold, i.e. at the bottom of the ‘U’:
with n th,min in 1019 m−3, IP in MA, BT in T and R, a in m. The expression agrees broadly with published values from C-Mod, AUG, JET and other devices (Ryter et al. Reference Ryter, Barrera Orte, Kurzan, McDermott, Tardini, Viezzer, Bernert and Fischer2014). When evaluated for the centroid of the data set in figure 1, equation (2.2) results in the vertical dashed line. This expression includes positive dependence on B and negative dependence on machine size. For C-Mod and SPARC parameters, this formula suggests a transition to e−i decoupling at low values of Greenwald fraction: n/nG < 0.2.
The Ryter model asserts a critical ion heat flow that is linear with density, a result that is found experimentally on both AUG and C-Mod. Combination of the data sets from the two machines (Schmidtmayr et al. Reference Schmidtmayr, Hughes, Ryter, Wolfrum, Cao, Creely, Howard, Hubbard, Lin and Reinke2018) allowed a combined regression
with Qi ,th in MW, n in 1019 m−3, BT in T and S in m2, which is very similar in character to the power law in (2.1) particularly considering the exponents on the field and surface area terms. An equivalent expression for total power threshold can be obtained by assuming a fraction of loss of power that is convected through the edge in the ion channel, fi = Qi/P. For typical C-Mod L-mode discharges in the high-density branch, we typically assume strong collisional coupling between electrons and ions and an ion power fraction of fi = 0.5. Power balance calculations from transport simulations are generally consistent with this assumption (Schmidtmayr et al. Reference Schmidtmayr, Hughes, Ryter, Wolfrum, Cao, Creely, Howard, Hubbard, Lin and Reinke2018), allowing us to take P th = 2 × Qi ,th. Figure 1 shows that when this alternate expression is evaluated for C-Mod in the high-density branch, it loosely follows the experimental power threshold data, and is slightly more conservative than the ITPA expression.
Indications on AUG are that the critical ion heat flow required to initiate an L–H transition approximately doubles when going from D to H discharges, consistent with the general isotope trend observed in total P th. (Ryter et al. Reference Ryter, Rathgeber, Barrera Orte, Bernert, Conway, Fischer, Happel, Kurzan, McDermott and Scarabosio2013, Reference Ryter, Barrera Orte, Kurzan, McDermott, Tardini, Viezzer, Bernert and Fischer2014) This suggests that an isotope multiplier term 1/A could be reasonably applied to the scaling in (2.3), as is often done for (2.1).
2.3. Low-density limit for H-mode access
To explore H-mode power requirements for SPARC, we primarily use the ITPA scaling law in (2.1), modified accordingly for the assumed isotope mix. We anticipate this to be a useful estimate for P th, provided n > n th,min. Below that critical density, an increase in the P th estimate is required. Following the model of Ryter et al. (Reference Ryter, Barrera Orte, Kurzan, McDermott, Tardini, Viezzer, Bernert and Fischer2014), the details of the low-density branch (LDB) behaviour would be dependent on the mix of ion versus electron heating, and the details of transport. In the absence of these details, we can construct an ad hoc correction term to apply to the LDB, i.e.
where the density correction term is inspired by the n 2 dependence of the ion–electron energy exchange term, and is applied only for n < n th,min. As shown in figure 1, such a correction added to (2.1) does a respectable job capturing the experimental trend on C-Mod (dashed blue curve).
Sample projections of power thresholds to SPARC are shown in figure 2 and compared with expected values of available heating for the device, for both (a) DD plasmas and (b) DT plasmas. In each case, the ITPA scaling law from (2.1), modified via (2.2) and (2.4), is shown in blue. The 1/A isotope correction is applied in figure 2(b), resulting in a 20% reduction of P th. SPARC will have 25 MW of auxiliary wave heating power in the ion cyclotron range of frequencies (ICRF) (Lin, Wright & Wukitch Reference Lin, Wright and Wukitch2020). At full field, the minimum projected P th is close to this available power level, indicating that the entry point to H-mode will have to be near n = n th,min=1.9 × 1020 m−3. The minimum L–H threshold power for DT is projected to be 21 MW, providing a margin for H-mode access. Before tritium is introduced to the device, operations and scenario development will have to utilize deuterium-only discharges. The projection to the full field DD discharge indicates P th,min > 25 MW. This makes H-mode access less likely for the DD scenario, although one cannot rule it out, given the level of scatter in actual power threshold observed in experiments, relative to scaling laws (see, for example, figure 1). An effective ICRF heating scheme exists for 2/3 field operation at 8 T, which does have a suitable margin for L–H access. Therefore, the 8 T DD discharge is a likely candidate for initial H-mode physics investigation on SPARC.
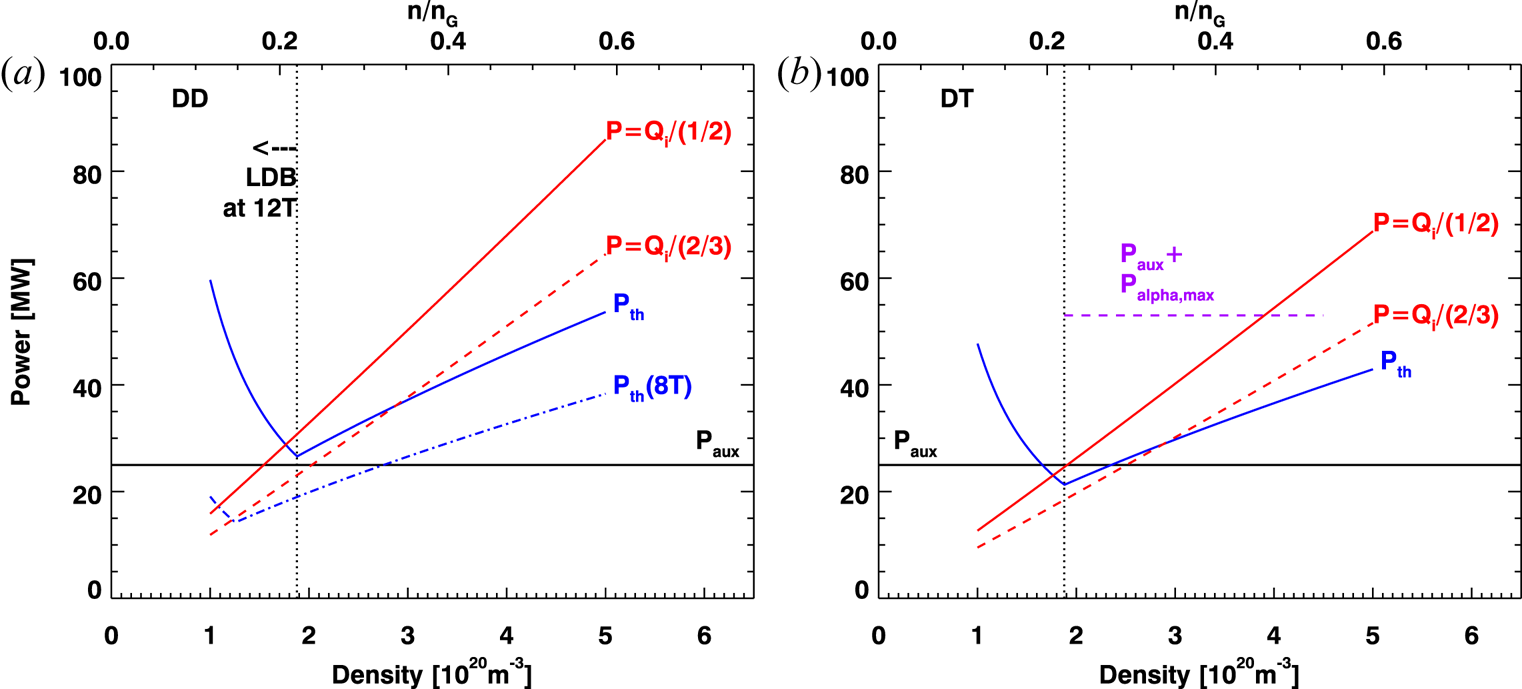
Figure 2. SPARC power threshold projections versus density in (a) DD and (b) DT operation. Blue curves represent the standard adopted for SPARC projections, a combination of expressions in (2.1), (2.2) and (2.4). Red curves represent projections using the expression for critical ion heat flow in (2.3) under assumptions that Qi = 0.5 × P (solid) and Qi = 0.67 × P (dashed). The curves in (b) also factor in a 1/A isotope scaling for power requirements. All curves are calculated using the baseline SPARC baseline parameters, except for the 8 T P th curve in (a). Horizontal lines indicate both the nominal auxiliary power available (25 MW) as well as the maximum heating power available in DT when alpha power is included.
The ITPA scaling law in (2.1) remains the best accepted empirical scaling, owing to its multimachine nature and application on many subsequent devices. The projection of the LDB onset given by (2.2) has also shown an acceptable level of cross-machine validation. As they are broadly tested across tokamaks, these scalings have been chosen to inform the SPARC design, and inform the plasma operational contour analyses detailed in Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020) and Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020). At the same time, it is of interest to track the projections obtained from the ion heat flow model. Power requirements based on (2.3) are shown in figure 2 for both DD and DT, with the latter adding a 1/A isotope correction. Two values of ion heat flow fraction are assumed: fi = 1/2 (similar to the typical C-Mod assumption) and fi = 2/3, which may better approximate a strongly ion-heated scenario. The L–H power requirements using these assumptions are similar to projections from the ITPA scaling law, for the nominal access condition of n = n th,min, but are significantly larger at higher density, owing to stronger dependence on n seen in (2.3) versus (2.1). An important finding is that a high ratio of ion heat flow to total power can significantly lower the overall power requirement. This is seen in figure 2 by comparing the dashed red and solid blue curves at n ~ 2 × 1020 m−3. The ICRF heating technique on SPARC will use 120 MHz RF minority heating on 3He (Lin et al. Reference Lin, Wright and Wukitch2020), which is projected to heat ions efficiently. Integrated simulations of the DT H-mode predict the majority of the edge heat flux to be in the ion channel (Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020).
Inspection of figure 2 points to an additional consideration of H-mode sustainment. There is no validated projection for H–L back-transition power threshold in the same way that the ITPA scaling law provides for the L–H power. However, once in H-mode, maintaining power above P th (calculated at the increased density) generally grants confidence that H-mode confinement will be sustained, although reductions in H-factor and changes in ELM character may be observed at P/P th near unity (Ryter et al. Reference Ryter, Fuchs, Schneider, Sips, Stäbler and Stober2008; Hughes et al. Reference Hughes, Loarte, Reinke, Terry, Brunner, Greenwald, Hubbard, LaBombard, Lipschultz and Ma2011; Knolker et al. Reference Knolker, Bortolon, Canal, Evans, Zohm, Abrams, Buttery, Davis, Groebner and Hollmann2018). On C-Mod, H-factor was shown to correlate with the ratio of net power flow through the pedestal P net to the calculated threshold power (Hughes et al. Reference Hughes, Loarte, Reinke, Terry, Brunner, Greenwald, Hubbard, LaBombard, Lipschultz and Ma2011). Although achieving this criterion becomes more challenging following the density increase associated with H-mode formation, in DT the sum of auxiliary power and the maximum available alpha power in H-mode provide headroom over the projected P th, as seen in figure 2(b).
2.4. Additional considerations for power threshold
Confidence in the various power threshold projections is earned through validation on multiple machines, and activities continue within the community to refine power threshold projections, particularly within the ITPA. As updates from these activities emerge, they may be considered for revised SPARC projections. Meanwhile, we address a few considerations of SPARC device features that might potentially modify the P th projection from the standard ITPA expression.
First, although single-null operation of SPARC is possible, a double-null equilibrium is preferred for purposes of divertor heat load sharing and maintaining high elongation. L–H P th scalings are well characterized only for single-null geometries with ion ![]() $B \times {\bf \nabla }B$ drift toward the X-point. We know from existing experimental work that balanced double-null operation does not obviously increase P th and can indeed reduce it. The reduction is significant in the case of low-aspect-ratio devices (Meyer et al. Reference Meyer, Carolan, Conway, Cunningham, Horton, Kirk, Maingi, Ryter, Saarelma and Schirmer2006, Reference Meyer, De Bock, Conway, Freethy, Gibson, Hiratsuka, Kirk, Michael, Morgan and Scannell2011) and more modest (perhaps 30%) in the case of conventional-aspect-ratio tokamaks (Meyer et al. Reference Meyer, Carolan, Conway, Cunningham, Horton, Kirk, Maingi, Ryter, Saarelma and Schirmer2006). Thus, provided good control of magnetic balance, the P th projection we use for SPARC is conservative. If magnetic balance drifts too far in the direction of a single X-point opposite the
$B \times {\bf \nabla }B$ drift toward the X-point. We know from existing experimental work that balanced double-null operation does not obviously increase P th and can indeed reduce it. The reduction is significant in the case of low-aspect-ratio devices (Meyer et al. Reference Meyer, Carolan, Conway, Cunningham, Horton, Kirk, Maingi, Ryter, Saarelma and Schirmer2006, Reference Meyer, De Bock, Conway, Freethy, Gibson, Hiratsuka, Kirk, Michael, Morgan and Scannell2011) and more modest (perhaps 30%) in the case of conventional-aspect-ratio tokamaks (Meyer et al. Reference Meyer, Carolan, Conway, Cunningham, Horton, Kirk, Maingi, Ryter, Saarelma and Schirmer2006). Thus, provided good control of magnetic balance, the P th projection we use for SPARC is conservative. If magnetic balance drifts too far in the direction of a single X-point opposite the ![]() $B \times {\bf \nabla }B$ direction, then significant increases in L–H power can be expected.
$B \times {\bf \nabla }B$ direction, then significant increases in L–H power can be expected.
Our projections are also not expected to increase due to the exclusive use of wave heating, as opposed to neutral beam injection (NBI), and the absence of driven rotation. The ITPA scaling law was fitted to a mix of beam-heated and wave-heated discharges across devices, including exclusively ICRF-heated cases on C-Mod (see again figure 1). The AUG findings discussed above point to a clear difference in threshold power for NBI versus electron cyclotron heated discharges, at low density, but this was attributed to the poor ion–electron equilibration in the LDB. Staying above n th,min, as well as providing a significant amount of ion heating with the ICRF, removes this as a concern on SPARC. Similarly, the lack of externally applied torque is not expected to raise the L–H power requirement. Scans of input torque on DIII-D have shown the zero crossing has substantially lower P th than the more typical case in which NBI power drives rotation in the co-IP direction (McKee et al. Reference McKee, Gohil, Schlossberg, Boedo, Burrell, deGrassie, Groebner, Moyer, Petty and Rhodes2009), and this has been linked experimentally to reduced edge toroidal rotation, which facilitates the formation of a sheared edge radial electric field (Gohil et al. Reference Gohil, Jernigan, Osborne, Scoville and Strait2010).
Magnetic field ripple, resulting from having discrete toroidal field coils, can affect plasma transport and influence rotation, and therefore is also a consideration for power thresholds. On JET, ripple at the outboard midplane separatrix was scanned up to 1.1%. Although NBI losses increased at the higher ripple value, once these power losses are accounted for, power threshold was unaffected (Andrew et al. Reference Andrew, Biewer, Crombe, Keeling, de la Luna, Giroud, Hawkes, Kempenaars, Korotkov and Meigs2008). On DIII-D a local ripple of 3% was induced by a toroidally localized coil set, to simulate the effects of an ITER test blanket module. With the coil energized P th did not change outside uncertainties (Gohil et al. Reference Gohil, Evans, Fenstermacher, Ferron, Osborne, Park, Schmitz, Scovolle and Unterberg2011). These relatively large levels of ripple exceed the target values for SPARC design. Ripple has been evaluated numerically for SPARC, mainly for the purpose of predicting ripple-induced fast ion losses (Scott et al. Reference Scott, Kramer, Snicker, Varje, Särkimäki, Tolman, Rodriguez-Fernandez and Wright2020). Considering both perfect alignment of coils and likely as-built displacements, the values of ripple remain below 0.5% at the nominal separatrix location, indicating low risk to H-mode access.
The effects of divertor geometry and X-point location on the L–H threshold power can vary significantly on a given tokamak, introducing in some cases stronger than normal deviations from observed P th, including significant reductions (Horton et al. Reference Horton, Vlases, Andrew, Bhatnagar, Chankin, Clement, Conway, Davies, de Haas and Ehrenberg1999; Fukuda et al. Reference Fukuda, Takizuka, Tsuchiya, Kamada and Asakura2000; Andrew et al. Reference Andrew, Hawkes, O'Mullane, Sartori, de Baar, Coffey, Guenther, Jenkins, Korotkov and Lomas2004, Reference Andrew, Biewer, Crombe, Keeling, de la Luna, Giroud, Hawkes, Kempenaars, Korotkov and Meigs2008; Gohil et al. Reference Gohil, Evans, Fenstermacher, Ferron, Osborne, Park, Schmitz, Scovolle and Unterberg2011; Ma et al. Reference Ma, Hughes, Hubbard, LaBombard and Terry2012, Maggi et al. Reference Maggi, Delabie, Biewer, Groth, Hawkes, Lehnen, de la Luna, McCormick, Reux and Rimini2014). No unifying picture that explains the results on all devices has emerged, although the influence on divertor parameters on the upstream radial electric field in the scrape-off layer is a candidate mechanism that is actively under study (Chankin et al. Reference Chankin, Delabie, Corrigan, Maggi and Meyer2017). The divertor effect remains one of the largest sources of variability in the projection of power threshold. The SPARC divertor is being designed to facilitate parallel heat flux mitigation via small inclination angle and strike point sweeping, and also to have a long outer leg to enable the creation of an X-point target (Kuang et al. Reference Kuang, Ballinger, Brunner, Canik, Creely, Gray, Greenwald, Hughes, Irby and LaBombard2020). This will create a significant variation on X-point and divertor geometry across various scenarios and even within a single discharge, and may influence the entry into H-mode.
3. Pedestal pressure predictions
3.1. Method for pedestal prediction
Integrated transport modelling of SPARC has been effective at predicting the performance of SPARC and validating 0D projections (Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020), informing the device design. A vital ingredient for these simulations is a reliable prediction for the temperature and density boundary condition at the periphery. We obtain these from a model H-mode pedestal calculated using the EPED model (Snyder et al. Reference Snyder, Groebner, Hughes, Osborne, Beurskens, Leonard, Wilson and Xu2011). EPED is the most widely validated predictive model available for the pedestal, having been tested on existing experiments spanning nearly two orders of magnitude in pedestal pressure (Groebner et al. Reference Groebner, Chang, Hughes, Maingi, Snyder, Xu, Boedo, Boyle, Callen and Canik2013; Snyder et al. Reference Snyder, Hughes, Osborne, Paz-Soldan, Solomon, Knolker, Eldon, Evans, Golfinopoulos and Grierson2019). The agreement between EPED predictions and experimental values of pedestal height is typically within 20% across devices, for pedestals constrained by magnetohydrodynamic (MHD) stability. This includes the largest tokamak, JET, operating with both a carbon wall and an ITER-like wall of beryllium and tungsten (Beurskens et al. Reference Beurskens, Frassinetti, Challis, Giroud, Saarelma, Alper, Angioni, Bilkova, Bourdelle and Brezinsek2014). The cross-machine validation of EPED extends to high-field and high-density regimes on Alcator C-Mod (Walk et al. Reference Walk, Snyder, Hughes, Terry, Hubbard and Phillips2012; Tolman et al. Reference Tolman, Hughes, Wolfe, Wukitch, LaBombard, Hubbard, Marmar, Snyder and Schmidtmayr2018), including the highest-pressure pedestals ever achieved on a tokamak (Hughes et al. Reference Hughes, Snyder, Reinke, LaBombard, Mordijck, Scott, Tolman, Baek, Golfinopoulos and Granetz2018). Extension of EPED to SPARC can be done with relatively high confidence. Though the absolute pressure on SPARC should exceed existing devices considerably, the pedestal beta and βN are within the range over which EPED has been validated.
EPED predicts the height and width of the pressure pedestal (p ped, Δ ped) as limited by criticality to kinetic ballooning mode and peeling–ballooning mode onset. The model equation for the pressure profile is a modified hyperbolic tangent function (Groebner et al. Reference Groebner, Baker, Burrell, Carlstrom, Ferron, Gohil, Lao, Osborne, Thomas and West2001), defined on coordinates of normalized poloidal flux ψ. Figure 3(a) gives an example of this function. It exhibits a region of steep gradient with width Δ, having a ‘foot’ at the location ψ = 1 and a ‘knee’ at ψ = 1 − Δ. The value of pressure at the knee defines p ped. Similarly, n ped is defined as the density at the knee. Unless otherwise noted, the values of pedestal parameters in this article are taken at the knee. EPED also returns pressure values further up the profile at ψ = 1 − 1.5 × Δ, which we refer to as p top and which get passed to the integrated transport model detailed in Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020).

Figure 3. (a) Visualization of the width and height parameters of the modified tanh fit used in the EPED model, using an arbitrary pressure profile having width Δ = 0.05 in normalized poloidal flux. In this article, quantities subscripted ‘ped’ are taken one pedestal width inside the LCFS and those subscripted ‘top’ are taken 1.5Δ inside the LCFS. (b) Scanning BT from 2 T to 12 T in a SPARC-sized tokamak, fixing edge q. The three scans are performed at indicated fG ,ped values. The purple triangle indicates the highest experimental pedestal pressure reported previously, and the toroidal field at which the result was obtained (Hughes et al. Reference Hughes, Snyder, Reinke, LaBombard, Mordijck, Scott, Tolman, Baek, Golfinopoulos and Granetz2018).
The pedestal pressure supplied by EPED is the maximum pedestal likely to be obtained, and is usually associated with a peeling–ballooning MHD stability boundary, which can be manifested experimentally either by Type I ELMs or in some cases by the formation of a quiescent H-mode (QH-mode) pedestal with an edge harmonic oscillation (EHO) (Burrell et al. Reference Burrell, West, Doyle, Austin, Casper, Gohil, Greenfield, Groebner, Hyatt and Jayakumar2005; Solomon et al. Reference Solomon, Burrell, Fenstermacher, Garofalo, Grierson, Loarte, McKee, Nazikian, Osborne and Snyder2015). A strength of the model is that its outputs are determined by a relatively simple set of scalar inputs. Most inputs are part of the design of a particular discharge: Bt, Ip, R, a, κ, δ, mi. Other inputs require additional prediction or estimation: n ped, βN ,global, Z eff. Pedestal density is an example of an input with significant uncertainty, and which, as shown in the following, has a substantial effect on predicted pressure. To the extent pedestal density can be controlled, it can be considered an optimization parameter for pedestal and overall fusion performance.
A persistent finding from pedestal stability calculations, as embodied in EPED, is that low-collisionality H-modes with sufficiently strong shaping exhibit a positive p ped scaling with both toroidal and poloidal field (Snyder et al. Reference Snyder, Solomon, Burrell, Garofalo, Grierson, Groebner, Leonard, Nazikian, Osborne and Belli2015; Hughes et al. Reference Hughes, Snyder, Reinke, LaBombard, Mordijck, Scott, Tolman, Baek, Golfinopoulos and Granetz2018). A consequence of this is that one may fix a tokamak plasma of a certain shape and safety factor, and obtain a much stronger than linear increase in p ped with BT. Figure 3(b) shows an example of such scans, which begin with EPED pedestal predictions using a set of plasma parameters characteristic of a high-performance mid-size tokamak, similar in scale to SPARC: BT = 2 T, Ip = 0.9 MA, R = 1.67 m, a = 0.58 m, κ = 1.8, δ = 0.55, mi = 2, βN = 2.8, Z eff = 1.8. Three values of input n ped in units of 1019 m−3 are chosen: 2.5, 5.0 and 7.5. From these three base cases, the value of BT is scanned to 12 T, with Ip and n ped increased in proportion so that the values of safety factor q and pedestal Greenwald fraction fG ,ped are held fixed. The remaining EPED inputs are held fixed. The strong dependence on toroidal field in all cases is shown by the fitted power law curves. Tripling the toroidal field and current allows this equilibrium to access pedestal pressure characteristic of the largest value achieved previously (Hughes et al. Reference Hughes, Snyder, Reinke, LaBombard, Mordijck, Scott, Tolman, Baek, Golfinopoulos and Granetz2018) (purple triangle), and the full six-fold increase grants access to pedestal pressure in excess of 0.3 MPa.
The pressure pedestal prediction from EPED is quite sensitive to the input n ped, as well as Z eff, because these largely determine the collisionality regime, and collisionality impacts the self-consistent bootstrap current in the edge barrier. The favourable scaling with both BP and BT is enabled by maintaining low ν*, which results in a pedestal limited by low-n peeling modes (i.e. modes driven primarily by the bootstrap current gradient in the edge barrier region). For higher ν*, EPED tends to predict a transition to a pedestal limited by higher-n modes more ballooning in nature, which can decrease the attainable p ped, a result that has been validated in experiments (Snyder et al. Reference Snyder, Solomon, Burrell, Garofalo, Grierson, Groebner, Leonard, Nazikian, Osborne and Belli2015; Hughes et al. Reference Hughes, Snyder, Reinke, LaBombard, Mordijck, Scott, Tolman, Baek, Golfinopoulos and Granetz2018). For sufficiently strong plasma shaping, it is feasible to access a peeling-limited branch at higher density. This is referred to as super H-mode when it is associated with multivalued pedestal pressure predictions from EPED at a given density (Snyder et al. Reference Snyder, Solomon, Burrell, Garofalo, Grierson, Groebner, Leonard, Nazikian, Osborne and Belli2015; Snyder et al. Reference Snyder, Hughes, Osborne, Paz-Soldan, Solomon, Knolker, Eldon, Evans, Golfinopoulos and Grierson2019). SPARC design uses conservative physics choices and does not seek super H-mode solutions to meet its performance goals. For the purposes of SPARC pedestal prediction, we take only the lowest value of pressure predicted by EPED at a given density, noting that super H-mode solutions could provide an avenue for further performance optimization if the parametric trajectory of the pedestal density can be controlled.
3.2. EPED predictions informing SPARC device design
Scanning the input n ped in EPED allows us to verify that SPARC remains on the peeling limited branch. An early operating point chosen for SPARC (V0) (Greenwald et al. Reference Greenwald, Whyte, Bonoli, Hartwig, Irby, LaBombard, Marmar, Minervini, Takayasu and Terry2018) was evaluated with EPED in order to identify the detailed density dependence of the pressure pedestal. The V0 parameters that differ from the V2 parameters in table 1 are as follows: BT = 12 T, Ip = 7.5 MA, R = 1.65 m, a = 0.5 m, κ = 1.8 and δ = 0.4. V0 is smaller, is more weakly shaped and supports lower plasma current. Figure 4 illustrates the results of the scan, indicating predicted (a) pedestal pressure, both in terms of p ped and p top, and (b) pedestal width. As seen in figure 4, the predicted pedestal width and pressure were found to increase with n ped for the range of assumed operating densities, which spans about 2–4 × 1020 m−3. This is a signature of peeling limited modes limiting the pedestal, and is very favourable to upward excursions in density, which do not result in a loss of performance. In contrast, operation at higher densities (fG ,ped > 0.55) would make the pedestal more ballooning limited, and lead to a p ped that decreases with increasing n ped. For this and subsequent iterations, we have verified sufficient distance between the prospective operating density and the ballooning branch. This follows naturally because all iterations of SPARC design have aimed to be far from the Greenwald density limit (i.e. n/nG < 0.4).
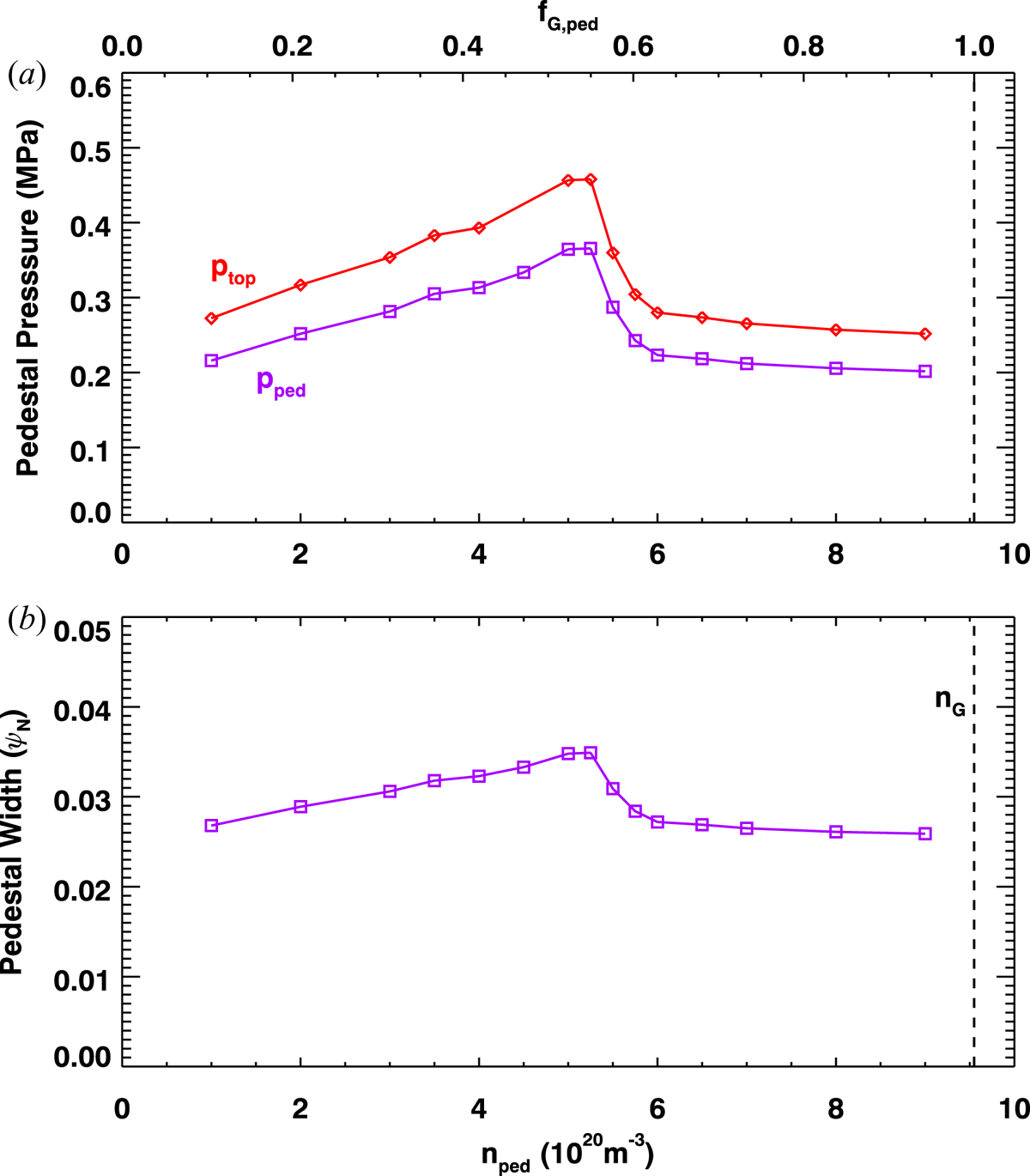
Figure 4. EPED density scan for SPARC V0 illustrating both peeling and ballooning limited branches: (a) p ped and p top as a function of assumed pedestal density (and pedestal Greenwald fraction); and (b) pedestal width. The density dependence is familiar from simulation + analysis of existing devices.
Although elongation appears in confinement scaling laws, higher-order shaping parameters such as triangularity and squareness are notably absent. Nonetheless higher triangularity is shown in experiments to improve pedestal height and overall performance in H-mode (Osborne et al. Reference Osborne, Ferron, Groebner, Lao, Leonard, Mahdavi, Maingi, Miller, Turnbull, Wade and Watkins2000; Maggi et al. Reference Maggi, Saarelma, Casson, Challis, de la Luna, Frassinetti, Giroud, Joffrin, Simpson and Beurskens2015), and this largely may be understood through the improvement in pedestal stability (Snyder et al. Reference Snyder, Wilson, Osborne and Leonard2004). Starting from the modestly shaped case (delta = 0.4) in figure 4, we calculate the p ped change in an increasing scan of triangularity. The results shown in figure 5(a) indicate significant improvement with triangularity for fG ,ped < 0.4. This pedestal enhancement motivated consideration of stronger shaping in subsequent SPARC design iterations (such as the current V2 iteration), as it would increase the maximum possible performance of the device. Although in this particular scan the available operational space in the peeling branch is reduced from fG ,ped < 0.55 to fG ,ped < 0.4, a larger window for high-pressure operation is obtained by increasing elongation, as in figure 5(b), which results in increased edge q.

Figure 5. EPED predictions can directly probe shaping influence on SPARC performance. (a) The V0 case from figure 4 re-evaluated with progressively increasing triangularity (0.4–0.6). (b) The δ = 0.55 case re-evaluated with increasing elongation (1.8–1.9).
As the SPARC design parameters were iterated toward V2, predictions for pedestal height were embedded self-consistently into performance calculations (Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020), and were thus able to reflect the equilibrium shape changes that occurred at each step. Realistic equilibria from TRANSP were used to generate the shaping inputs to EPED. Typical SPARC discharges under consideration are strongly elongated and have two poloidal field nulls, resulting in δ and κ being significantly larger when evaluated on the separatrix, rather than on slightly interior flux surfaces inside the pedestal region. Given the increase in pressure pedestal with higher shaping shown previously, we chose a conservative approach and adopted the slightly lower values of δ and κ that are calculated inside the pedestal region, at ψ = 0.995 (see table 1). Requirements on divertor heat flux mitigation make strike point sweeping necessary, which introduces time-dependent triangularity values during a SPARC discharge (Kuang et al. Reference Kuang, Ballinger, Brunner, Canik, Creely, Gray, Greenwald, Hughes, Irby and LaBombard2020). The strike point sweep extrema are illustrated in figure 6(a) with comparison with the V2 baseline. These sweeps alter the shape parameters from [δ 995 = 0.49, κ 995 = 1.91] to [δ 995 = 0.53, κ 995 = 1.88] for the inward swing and to [δ 995 = 0.44, κ 995 = 1.91] for the outward swing.

Figure 6. (a) Divertor region separatrix contours from SPARC V2 model equilibria: baseline (black) and with excursions from strike point sweeping (red, blue). (b) Pedestal predictions for the equilibria in (a). The attainable pedestal performance significantly exceeds that of the V0 plasma (purple). The pedestal Greenwald fraction on the upper x-axis applies only to the V2 scans.
Using these values as input to EPED, the p ped predictions for V2 are calculated in figure 6(b). For the baseline (black squares) as well as the strike point extrema (red, blue), clear improvement is seen relative to the V0 design (purple), with higher obtainable pedestal pressure and a transition to the lower-performance ballooning-limited regime pushed to higher density (not shown). SPARC V2 remains on the peeling-limited branch for pedestal densities over a factor of two higher than the target value (vertical dashed line), indicating that modestly increasing the operating H-mode density will not degrade pedestal performance. Note that these calculations assume up–down asymmetry of the equilibrium such that the upper and lower triangularities are equal. However, it is likely possible to design sweeps of the upper and lower divertor strike points which are out of phase, such that the average triangularity deviates less from that of the baseline, and the EPED predictions remain closer to the black curve in figure 6(b), throughout the sweep. This may be desirable both for maintaining high pedestal pressure and for avoiding the onset of edge MHD.
4. Expectations for edge transients
4.1. Unmitigated ELMs
Tokamaks commonly exhibit periodic ELMs (Leonard Reference Leonard2014) in high-temperature H-modes. The typical ELM accompanying high performance is a Type I ELM, which manifests as a prompt drop in the plasma pressure at the top of the H-mode pedestal, and is accompanied by a burst of energy and particles onto the tokamak divertor, as well as onto main chamber surfaces. The pedestal regulation from ELMs would not directly limit SPARC performance, based on the pedestal projections in § 3, which yield favourable overall confinement projections satisfying the SPARC mission of achieving Q > 2 (Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020). ELMs can be effective at removing impurities from the core plasma, however large ELMs create additional power and particle handling challenges for PFCs, and ELM size can correlate with pedestal pressure. We now turn to projecting the characteristics of natural ELMs, absent of external mitigation schemes, to guide PFC design, particularly components in the divertor.
First, we seek to quantify the size of an ELM, ΔW ELM, which is equal to the ELM-induced drop in pedestal stored energy, W ped = 3/2 × p ped × V plasma. Here W ped is calculated using the EPED predictions in § 3 and shown in figure 7(a) along with the pedestal temperature. Multimachine studies conducted to inform ITER have concluded that the fractional ELM size ΔW ELM / W ped correlates inversely with collisionality at the top of the pedestal ![]() $v_{\textrm{ped}}^\ast $ and this relationship is adopted to project unmitigated ELM size to ITER (Loarte et al. Reference Loarte, Saibene, Sartori, Campbell, Becoulet, Horton, Eich, Herrmann, Matthews and Asakura2003, Reference Loarte, Lipschultz, Kukushkin, Matthews, Stangeby, Asakura, Counsell, Federici, Kallenbach and Krieger2007). Figure 7(b) indicates the neoclassical collisionality calculated using pedestal parameters. From inspection of Loarte et al.'s (Reference Loarte, Lipschultz, Kukushkin, Matthews, Stangeby, Asakura, Counsell, Federici, Kallenbach and Krieger2007) figure 17, a range of projected ΔW ELM / W ped values can be determined and used to compute a range of projected ΔW ELM as a function of ne ,ped. The minimum and maximum values are shown in figure 7(c), with the dashed verticals signifying points that have P th > P aux + P alpha,max and that are therefore likely inaccessible. At the SPARC design density, these assumptions give 1.4 < ΔW ELM[MJ] < 2.2 with significant spread arising from the scatter in the multimachine data (Loarte et al. Reference Loarte, Lipschultz, Kukushkin, Matthews, Stangeby, Asakura, Counsell, Federici, Kallenbach and Krieger2007). Were the pedestal pressure at time of ELM to be less than the EPED value of p ped,
$v_{\textrm{ped}}^\ast $ and this relationship is adopted to project unmitigated ELM size to ITER (Loarte et al. Reference Loarte, Saibene, Sartori, Campbell, Becoulet, Horton, Eich, Herrmann, Matthews and Asakura2003, Reference Loarte, Lipschultz, Kukushkin, Matthews, Stangeby, Asakura, Counsell, Federici, Kallenbach and Krieger2007). Figure 7(b) indicates the neoclassical collisionality calculated using pedestal parameters. From inspection of Loarte et al.'s (Reference Loarte, Lipschultz, Kukushkin, Matthews, Stangeby, Asakura, Counsell, Federici, Kallenbach and Krieger2007) figure 17, a range of projected ΔW ELM / W ped values can be determined and used to compute a range of projected ΔW ELM as a function of ne ,ped. The minimum and maximum values are shown in figure 7(c), with the dashed verticals signifying points that have P th > P aux + P alpha,max and that are therefore likely inaccessible. At the SPARC design density, these assumptions give 1.4 < ΔW ELM[MJ] < 2.2 with significant spread arising from the scatter in the multimachine data (Loarte et al. Reference Loarte, Lipschultz, Kukushkin, Matthews, Stangeby, Asakura, Counsell, Federici, Kallenbach and Krieger2007). Were the pedestal pressure at time of ELM to be less than the EPED value of p ped, ![]() $v_{\textrm{ped}}^\ast $ would increase and the estimated range of ΔW ELM would fall accordingly.
$v_{\textrm{ped}}^\ast $ would increase and the estimated range of ΔW ELM would fall accordingly.

Figure 7. (a) Pedestal stored energy and pedestal temperature versus assumed pedestal density. (b) Pedestal neoclassical collisionality used to project ΔW ELM / W ped. (c) Range in ELM energy content projected using multimachine data from Loarte et al. (Reference Loarte, Lipschultz, Kukushkin, Matthews, Stangeby, Asakura, Counsell, Federici, Kallenbach and Krieger2007). (d) Projected range in ELM frequency.
Second, using the projections described previously, we can estimate a range of ELM frequency f ELM, based on experimental findings that Type I ELMs tend to transport a fraction of total heating power (Hermann Reference Hermann2002), such that
where Cf ranges from 0.2 to 0.4 (Leonard et al. Reference Leonard, Herrmann, Itami, Lingertat, Loarte, Osborne and Suttrop1999). Figure 7(d) illustrates the range in f ELM for SPARC using the spread in Cf and ΔW ELM as inputs, and taking a realistic range for P heat. At each density, the maximum value of P heat is taken to be P aux + P alpha,max, and the minimum value is taken as the lesser of P aux + P alpha,max and P th. At the design density, we project a range of 2.7 < f ELM[Hz] < 15.0. Increased ELM frequency would be expected if the pressure pedestal was below the EPED prediction, and the ELM energy was proportionally lower.
Megajoule-class ELMs will introduce a significant regular perturbation on the pedestal boundary condition. A periodic drop in the pedestal, and rebuild, have not to date been included in time-dependent simulations of SPARC performance, and represent an opportunity for further development. Another need is to relate these pedestal energy losses to transient heat loads on divertor surfaces. Here we adopt a semi-empirical approach rooted in multimachine database analysis and use a scaling developed for the peak energy fluence ε ||,peak, which is just the time integral of the instantaneous parallel heat flux associated with an ELM (Eich et al. Reference Eich2017). A database of AUG, JET and MAST ELM energy fluence data is well represented by
where pe is the pedestal electron pressure (Pa), R geo is the geometric major radius (m) and q edge is the edge cylindrical safety factor. Here C is a factor that ranges from 1 to 3, where C = 3 captures the upper bound of the fluences in the data set and C = 1 captures the lower bound. Using the projections described previously and approximating pe = p ped/2, we obtain a peak energy fluence of 11–32 MJ m−2, which is similar in magnitude to projections for ITER (Eich et al. Reference Eich2017). Based on the database used to generate (4.2), ELM loads are statistically larger for larger values of W ELM/W plasma, i.e. ~10% rather than ~2%. Unmitigated ELMs on SPARC are likely to be at the high end of this range. Using a set of assumptions for the spatial and temporal distribution of this energy, a range of surface heat flux factor can be calculated and compared with the limits of candidate divertor materials (Kuang et al. Reference Kuang, Ballinger, Brunner, Canik, Creely, Gray, Greenwald, Hughes, Irby and LaBombard2020). To increase margin with respect to the ELM loading limits imposed by divertor PFCs, ELM mitigation schemes require consideration in SPARC.
4.2. Implications for performance with ELM mitigation
Mitigation or even full suppression of ELMs is feasible in tokamaks, both through extrinsic ELM control strategies (Lang et al. Reference Lang, Loarte, Saibene, Baylor, Becoulet, Cavinato, Clement-Lorenzo, Daly, Evans and Fenstermacher2013) and operation in intrinsically ELM-suppressed regimes (Lang et al. Reference Lang, Loarte, Saibene, Baylor, Becoulet, Cavinato, Clement-Lorenzo, Daly, Evans and Fenstermacher2013; Maingi Reference Maingi2014). Mitigation of ELMs typically involves the reduction of ELM magnitude, and often an increase in ELM repetition rate, using auxiliary means. One potential mitigation scheme for SPARC would involve pacing the ELMs with pellet injection (Lang et al. Reference Lang, Conway, Eich, Fattorini, Gruber, Günter, Horton, Kalvin, Kallenbach and Kaufmann2004; Romanelli, Kamendje on behalf of JET-EFDA Contributors Reference Romanelli and Kamendje2009). One necessary requirement for this technique would be the regular injection of pellets at frequency f pellet > f ELM (i.e. in the 20 Hz range or larger). Work is also ongoing to evaluate the feasibility of applying resonant magnetic perturbations (RMPs), which have had success on other devices in mitigating ELMs (Evans et al. Reference Evans, Moyer, Thomas, Watkins, Osborne, Boedo, Doyle, Fenstermacher, Finken and Groebner2004; Liang et al. Reference Liang, Koslowski, Thomas, Nardon, Alper, Andrew, Andrew, Arnoux, Baranov and Bécoulet2007; Suttrop et al. Reference Suttrop, Eich, Fuchs, Günter, Janzer, Herrmann, Kallenbach, Lang, Lunt and Maraschek2011; Jeon et al. Reference Jeon, Park, Yoon, Ko, Lee, Lee, Yun, Nam, Kim and Kwak2012; Kirk et al. Reference Kirk, Chapman, Liu, Cahyna, Denner, Fishpool, Ham, Harrison, Liang and Nardon2013; Sun et al. Reference Sun, Liang, Liu, Gu, Yang, Guo, Shi, Jia, Wang and Lyu2016). Full suppression of ELMs is also possible via application of RMPs, although the window for suppression is narrower than that for mitigation. Error field correction coils currently being designed for SPARC are planned to be capable also of introducing n = 3 RMPs, at an amplitude sufficient to satisfy the commonly used vacuum island overlap width criterion for complete ELM suppression (Fenstermacher et al. Reference Fenstermacher, Evans, Osborne, Schaffer, Aldan, deGrassie, Gohil, Joseph, Moyer and Snyder2008; Evans et al. Reference Evans, Orlov, Wingen, Wu, Loarte, Caspar, Schmitz, Saibene, Schaffer and Daly2013). The ELM energy loading study (Eich et al. Reference Eich2017) used to generate (4.2) included analysis of mitigated regimes and determined that this expression for ELM energy fluence was equally valid, i.e. the ELM load on the divertor continued to scale with the pedestal pressure under mitigation. There are also several demonstrated high-performance regimes with intrinsic ELM suppression. Examples include EDA H-mode (Hubbard et al. Reference Hubbard, Boivin, Granetz, Greenwald, Hughes, Hutchinson, Irby, LaBombard, Lin and Marmar2001; Hughes et al. Reference Hughes, Snyder, Walk, Davis, Diallo, LaBombard, Baek, Churchill, Greenwald and Groebner2013), I-mode (Whyte et al. Reference Whyte, Hubbard, Hughes, Lipschultz, Rice, Marmar, Greenwald, Cziegler, Dominguez and Golfinopoulos2010; Hughes et al. Reference Hughes, Snyder, Walk, Davis, Diallo, LaBombard, Baek, Churchill, Greenwald and Groebner2013; Walk et al. Reference Walk, Hughes, Hubbard, Terry, Whyte, White, Baek, Reinke, Theiler and Churchill2014), QH-mode with EHOs (Burrell et al. Reference Burrell, West, Doyle, Austin, Casper, Gohil, Greenfield, Groebner, Hyatt and Jayakumar2005; Solomon et al. Reference Solomon, Burrell, Fenstermacher, Garofalo, Grierson, Loarte, McKee, Nazikian, Osborne and Snyder2015; Wilks et al. Reference Wilks, Garofalo, Diamond, Guo, Hughes, Burrell and Chen2018) and wide pedestal QH-mode (Burrell et al. Reference Burrell, Barada, Chen, Garofalo, Groebner, Muscatello, Osborne, Petty, Rhodes and Snyder2016). Future work will explore the feasibility of access to these regimes. As in the case of ELM mitigation, a reduction in pedestal pressure is often (though not always) observed with intrinsic ELM suppression.
Because techniques we attempt to reduce the ELM loads in SPARC will likely result in a reduction in pedestal pressure below the unmitigated ELMy H-mode limit (i.e. what is predicted using EPED), it is important to account for this ‘penalty’ on the pedestal height when projecting the performance of a particular scenario. This pedestal reduction has been investigated for SPARC using the previously discussed integrated modelling tools, in which the temperature pedestal is tuned below the default prediction from EPED, while leaving the target density the same (Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020). The reduction of maximum ELM energy fluence is shown in table 2, alongside the resulting reduction in fusion gain and model H-factor. Because SPARC is designed with significant performance margin, even a stringent ELM mitigation or suppression technique that halves the pedestal pressure will still allow the device to meet its performance mission.
Table 2. Reduced ELM energy fluence and core performance from downgrading the EPED pedestal prediction by one-third and one-half.

5. Conclusions and future directions
The discussion presented here has shown that a combination of empirical scalings and modelling can be used to constrain performance projections for the SPARC tokamak, with a focus on the V2 design. In keeping with a conservative design philosophy, we have chosen models for H-mode access, pedestal height and ELM size that have been validated across multiple devices, and largely conform to community standards for projection to ITER. Accessing high-performance discharges on SPARC will test all these models in a new kind of fusion environment, on a device that uses very high magnetic fields at modest size, combines low collisionality with high absolute density and derives a significant amount of its heating power from fusion alpha particles. Insights gained from validating these models in the SPARC tokamak has the potential to significantly improve our confidence in model projections to future devices, including fusion pilot plant concepts.
H-mode access is computed using a standard ITPA scaling law in (2.1), with a modification that significantly increases the power requirement at n < n th,min. In the baseline 12.2 T DT discharge, we find H-mode to be accessible with some margin using available auxiliary power. Projections indicate a range in density of 1.7–2.3 × 1020 m−3 in L-mode at which H-mode triggering is likely with 25 MW of coupled ICRF. H-mode access in DD discharges may require operation at reduced field, e.g. 8 T. Following the L–H transition, increased core particle content will raise the value of P th, and we thus expect H-mode sustainment to require significant alpha heating. An alternate empirical scaling, based in the physics of a critical ion heat flow, is also assessed in SPARC, and suggests that P th for the L–H transition could be lower than anticipated, given enough ion heating. Because the ion heat scaling in (2.3) is only partially validated across devices, and because it is not readily translated to an absolute power requirement, it is not used to guide the device design. We are actively pursuing refinements to SPARC power threshold projections, based on emerging experimental and modelling developments in the community.
The EPED model generates a set of pressure pedestal predictions given SPARC operational parameters and assumptions for the pedestal density. These predictions support the high field approach by demonstrating a stronger than linear scaling of p ped with BT (at fixed q 95) in a medium sized, moderately shaped tokamak. Pedestal performance optimization is straightforward with EPED as design parameters are changed, and the positive influence of shaping (δ,κ) is clearly demonstrated. This influence propagates through integrated core performance modelling, and is internalized in design iterations. Partly because of this, as SPARC V0 evolved to V2, stronger shaping parameters were realized. Throughout the evolution of the design, we found that at targeted Greenwald fractions, the H-mode pedestal remained on the peeling-limited branch of operation found at low ![]() $v_{\textrm{ped}}^\ast $. Thus, pedestal performance is very favourable, and T ped is stable to upward excursions of density.
$v_{\textrm{ped}}^\ast $. Thus, pedestal performance is very favourable, and T ped is stable to upward excursions of density.
Some uncertainties remain in the pedestal predictions for SPARC. One physics gap is the ability to predict the structure of the density pedestal. Currently n ped is an input to be scanned, because further development is needed before we can make believable predictions for the pedestal density. These will depend on accurate models for particle source rate from both edge fuelling and pellet injection, as well as on better characterization of diffusive and convective (including inward) particle transport in the pedestal. Improved models for the density pedestal could allow us to relate the pedestal density to the separatrix density, providing a better means of coupling with divertor/SOL models. We note that significant edge fuelling has been a regular requirement on many devices for managing core impurity accumulation and stationarity (Kallenbach et al. Reference Kallenbach, Dux, Mayer, Neu, Pütterich, Bobkov, Fuchs, Eich, Giannone and Gruber2009; Nunes et al. Reference Nunes, Lomas, McDonald, Saibene, Sartori, Voitsekhovitch, Beurskens, Arnoux, Boboc and Eich2013; Beurskens et al. Reference Beurskens, Frassinetti, Challis, Giroud, Saarelma, Alper, Angioni, Bilkova, Bourdelle and Brezinsek2014; Nunes on behalf of the JET Contributors Reference Nunes2016). Pedestal pressure degradation and confinement loss is often observed in such cases and has been linked to an outwardly shifted density pedestal (Hughes et al. Reference Hughes, Loarte, Reinke, Terry, Brunner, Greenwald, Hubbard, LaBombard, Lipschultz and Ma2011; Dunne et al. Reference Dunne, Potzel, Reimold, Wischmeier, Wolfrum, Frassinetti, Beurskens, Bilkova, Cavedon and Fischer2017; Stefanikova et al. Reference Stefanikova, Frassinetti, Saarelma, Loarte, Nunes, Garzotti, Lomas, Rimini, Drewelow and Kruezi2018; Frassinetti et al. Reference Frassinetti, Dunne, Sheikh, Saarelma, Roach, Stefanikova, Maggi, Horvath, Pamela and de la Luna2019). In H-modes limited by peeling–ballooning modes, the degradation may be explained by reduced stabilization of higher n peeling–ballooning modes, which is a consequence of reduced pedestal bootstrap current and magnetic shear. As noted by Frassinetti et al. (Reference Frassinetti, Dunne, Sheikh, Saarelma, Roach, Stefanikova, Maggi, Horvath, Pamela and de la Luna2019) for low collisionality and high triangularity, as the dominant instabilities in the pedestal shift to the lower n peeling branch, this effect is expected to become less important. The design point of SPARC is such that it is solidly on the peeling branch and, therefore, we expect radial shifts of the density pedestal to be benign for MHD stability. Future work will test this expectation with full stability calculations using variable density pedestal structure.
Other factors that could cause departures from EPED predictions include fundamental changes to the stability of turbulent modes, which may result in pedestals not limited by peeling–ballooning modes, and which have differing limits on pedestal gradient or width. Such mechanisms are likely already present in intrinsically ELM-suppressed regimes studied on existing devices (Maingi Reference Maingi2014) and may even play a strong role in a subset of JET ELMy H-modes with high gas puff, for which Frassinetti et al. (Reference Frassinetti, Dunne, Sheikh, Saarelma, Roach, Stefanikova, Maggi, Horvath, Pamela and de la Luna2019) shows experimental p ped approximately 30% below EPED predictions. In addition, mitigation schemes such as ELM pacing and RMP application will most likely reduce the pedestal. Given the requirement for ELM mitigation and additional uncertainties in the density profile discussed previously, we routinely take the EPED prediction to be the maximum achievable pressure pedestal. The performance margin built into SPARC allows it to meet its Q > 2 goal even with up to a 2× reduction in p ped from the EPED prediction. Future work will include development of empirical models for the pedestals not limited by peeling–ballooning modes, and also access conditions to those regimes in terms of power and density requirements.
Acknowledgements
This work was funded by Commonwealth Fusion Systems under RPP005. Alcator C-Mod data were acquired and analysed prior to 2016 under DoE Award DE-FC02-99ER54512. Part of the data analysis was performed using the OMFIT integrated modelling framework (Meneghini et al. Reference Meneghini, Smith, Lao, Izacard, Ren, Park, Candy, Wang, Luna and Izzo2015) Development and testing of EPED is supported by DE-FG02-95ER54309 and DE-FC02-06ER54873. We thank the SPARC Physics Basis group for helpful discussions, in particular, J. Rice and C. Paz-Soldan.
Editor William Dorland thanks the referees for their advice in evaluating this article.
Declaration of interests
The authors report no conflict of interest.













