Article contents
Numerical solution of nonlinear electron kinetic equation in self-similar variables
Published online by Cambridge University Press: 09 June 2011
Abstract
We present numerical solution of a fully nonlinear electron kinetic equation in self-similar variables, which on the one hand has all features of a ‘standard’ hydrodynamics (ratios of the electron mean free path to the scale length γ ≡ λC/L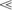 1), and on the other hand has no restriction on the smallness of the parameter γ. The self-similar variable approach reduces dimensionality of the space-dependent kinetic equation, thereby providing numerical analysis of the electron heat transport in the velocity space. The electron distribution structure and its super thermal power-law tail are examined.
1), and on the other hand has no restriction on the smallness of the parameter γ. The self-similar variable approach reduces dimensionality of the space-dependent kinetic equation, thereby providing numerical analysis of the electron heat transport in the velocity space. The electron distribution structure and its super thermal power-law tail are examined.
PACS number(s): 52.25.Dg, 52.65.Ff, 52.50.-b
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2011
References
- 2
- Cited by




