Article contents
Electron skin depth in low density plasmas
Published online by Cambridge University Press: 13 January 2020
Abstract
We rescale the generalized Ohm’s law and consider the limits that imply the electric field which moves with an ideal (inviscid and perfectly conducting) plasma be proportional to the time rate of change of the current density. Therefore, we show that those limits are satisfied by a sufficiently low electron number density, 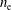 $n_{\text{e}}$. We also show that the electron–ion collision frequency,
$n_{\text{e}}$. We also show that the electron–ion collision frequency, 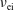 $\unicode[STIX]{x1D708}_{\text{ei}}$, is much smaller than the ion cyclotron frequency,
$\unicode[STIX]{x1D708}_{\text{ei}}$, is much smaller than the ion cyclotron frequency, 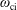 $\unicode[STIX]{x1D714}_{\text{ci}}$. The combination of that condition with the Lawson criterion for a typical deuterium–tritium fusion in ITER reveals a lower bound for the geometric mean of the confinement time,
$\unicode[STIX]{x1D714}_{\text{ci}}$. The combination of that condition with the Lawson criterion for a typical deuterium–tritium fusion in ITER reveals a lower bound for the geometric mean of the confinement time, 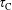 $\unicode[STIX]{x1D70F}_{\text{C}}$, and collision interval,
$\unicode[STIX]{x1D70F}_{\text{C}}$, and collision interval, 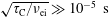 $\sqrt{\unicode[STIX]{x1D70F}_{\text{C}}/\unicode[STIX]{x1D708}_{\text{ei}}}\gg 10^{-5}~\text{s}$. For that reaction, we estimate that
$\sqrt{\unicode[STIX]{x1D70F}_{\text{C}}/\unicode[STIX]{x1D708}_{\text{ei}}}\gg 10^{-5}~\text{s}$. For that reaction, we estimate that 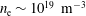 $n_{\text{e}}\sim 10^{19}~\text{m}^{-3}$, and contrast typical parameters of our fully ionized gas with those of warm, hot and thermonuclear plasmas. When, in addition,
$n_{\text{e}}\sim 10^{19}~\text{m}^{-3}$, and contrast typical parameters of our fully ionized gas with those of warm, hot and thermonuclear plasmas. When, in addition, 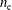 $n_{\text{e}}$ varies slowly in time and weakly in space, we generalize Alfvén’s theorem, by showing that the frozen-in condition holds true for an effective magnetic field, which depends on a finite electron skin depth. We perform a (divergenceless) helical perturbation on an axisymmetric equilibrium, to derive a dispersion relation in the cylindrical tokamak limit, and, subsequently, apply our analytical formulation to the peaked model, which assumes a logarithmic derivative profile for the poloidal component of the equilibrium magnetic field. In that formulation, the definition of the safety factor in terms of the effective field yields a shift in the magnetic surfaces. We find that the instability peak may triple that predicted on neglect of a finite electron mass. We also find that inertial effects may centuple the radius of the stable cylindrical column.
$n_{\text{e}}$ varies slowly in time and weakly in space, we generalize Alfvén’s theorem, by showing that the frozen-in condition holds true for an effective magnetic field, which depends on a finite electron skin depth. We perform a (divergenceless) helical perturbation on an axisymmetric equilibrium, to derive a dispersion relation in the cylindrical tokamak limit, and, subsequently, apply our analytical formulation to the peaked model, which assumes a logarithmic derivative profile for the poloidal component of the equilibrium magnetic field. In that formulation, the definition of the safety factor in terms of the effective field yields a shift in the magnetic surfaces. We find that the instability peak may triple that predicted on neglect of a finite electron mass. We also find that inertial effects may centuple the radius of the stable cylindrical column.
Keywords
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press 2020
References
- 1
- Cited by




