1 Introduction
Attaining high performance tokamak operation regimes is of primary interest for a future fusion reactor. Such a condition is usually achieved in the so-called tokamak H-mode (high confinement) regime. Besides the high confinement time, the H-mode is characterised by large pressure gradients located near the plasma boundary. These gradients favour the development of a particular kind of instability called the edge localised mode (ELM). Such type of perturbations are associated with rapid and violent bursts of energy and particles which can severely damage the plasma facing components with intolerable heat loads. An increasing interest has been therefore devoted to the study of the so-called quiescent high confinement mode (QH-mode). The QH-mode regime (Burrell et al.
Reference Burrell, Austin, Brennan, DeBoo, Doyle, Gohil, Greenfield, Groebner, Lao and Luce2002; Suttrop et al.
Reference Suttrop, Maraschek, Conway, Fahrbach, Haas, Horton, Kurki-Suonio, Lasnier, Leonard and Maggi2003, Reference Suttrop, Hynönen, Kurki-Suonio, Lang, Maraschek, Neu, Stäbler, Conway, Hacquin and Kempenaars2005) shares with the H-mode a large edge pressure pedestal (edge transport barrier) and high energy confinement time but without the presence of ELMs. These are replaced by a less dangerous continuous magnetohydrodynamic (MHD) activity called edge harmonic oscillation (EHO). The energy loads deposited by EHOs are much lower compared to the ones associated with ELMs. EHOs have low-
![]() $n$
toroidal number (e.g.
$n$
toroidal number (e.g.
![]() $n=1,2,3$
while ELMs are instead characterised by large
$n=1,2,3$
while ELMs are instead characterised by large
![]() $n$
values) and are always experimentally observed during the QH-mode operation (Burrell et al.
Reference Burrell, Austin, Brennan, DeBoo, Doyle, Fenzi, Fuchs, Gohil, Greenfield and Groebner2001, Reference Burrell, Austin, Brennan, DeBoo, Doyle, Gohil, Greenfield, Groebner, Lao and Luce2002, Reference Burrell, West, Doyle, Austin, Casper, Gohil, Greenfield, Groebner, Hyatt and Jayakumar2005; Suttrop et al.
Reference Suttrop, Conway, Fattorini, Horton, Kurki-Suonio, Maggi, Maraschek, Meister, Neu and Putterich2004; Solano et al.
Reference Solano, Lomas, Alper, Xu, Andrew, Arnoux, Boboc, Barrera, Belo and Beurskens2010).
$n$
values) and are always experimentally observed during the QH-mode operation (Burrell et al.
Reference Burrell, Austin, Brennan, DeBoo, Doyle, Fenzi, Fuchs, Gohil, Greenfield and Groebner2001, Reference Burrell, Austin, Brennan, DeBoo, Doyle, Gohil, Greenfield, Groebner, Lao and Luce2002, Reference Burrell, West, Doyle, Austin, Casper, Gohil, Greenfield, Groebner, Hyatt and Jayakumar2005; Suttrop et al.
Reference Suttrop, Conway, Fattorini, Horton, Kurki-Suonio, Maggi, Maraschek, Meister, Neu and Putterich2004; Solano et al.
Reference Solano, Lomas, Alper, Xu, Andrew, Arnoux, Boboc, Barrera, Belo and Beurskens2010).
These low-
![]() $n$
oscillations have been linked with kink/peeling modes (Connor et al.
Reference Connor, Hastie, Wilson and Miller1998) which are proposed as a possible candidate for the explanation of the appearance of these perturbations. Linear and nonlinear simulations of QH-mode DIII-D plasma discharges showed that kink/peeling modes are the main unstable modes in the nonlinear phase whose saturation leads to a three-dimensional stationary state with toroidal periodicity characterised by a low-
$n$
oscillations have been linked with kink/peeling modes (Connor et al.
Reference Connor, Hastie, Wilson and Miller1998) which are proposed as a possible candidate for the explanation of the appearance of these perturbations. Linear and nonlinear simulations of QH-mode DIII-D plasma discharges showed that kink/peeling modes are the main unstable modes in the nonlinear phase whose saturation leads to a three-dimensional stationary state with toroidal periodicity characterised by a low-
![]() $n$
number (generally
$n$
number (generally
![]() $n=1,2$
) (Liu et al.
Reference Liu, Huijsmans, Loarte, Garofalo, Solomon, Snyder, Hoelzl and Zeng2015). These low-
$n=1,2$
) (Liu et al.
Reference Liu, Huijsmans, Loarte, Garofalo, Solomon, Snyder, Hoelzl and Zeng2015). These low-
![]() $n$
modes are not the linearly most unstable modes in the linear phase, but they are driven by the nonlinear coupling with medium-
$n$
modes are not the linearly most unstable modes in the linear phase, but they are driven by the nonlinear coupling with medium-
![]() $n$
(
$n$
(
![]() ${\sim}3,4,5$
) harmonics (Liu et al.
Reference Liu, Huijsmans, Loarte, Garofalo, Solomon, Snyder, Hoelzl and Zeng2015).
${\sim}3,4,5$
) harmonics (Liu et al.
Reference Liu, Huijsmans, Loarte, Garofalo, Solomon, Snyder, Hoelzl and Zeng2015).
Steep edge pressure gradients are associated in the low collisionality regime with a large edge bootstrap current contribution which produces an edge flattening of the safety factor (
![]() $q$
) profile. Numerical studies of low-
$q$
) profile. Numerical studies of low-
![]() $n$
MHD modes in QH regime with a plateau in
$n$
MHD modes in QH regime with a plateau in
![]() $q$
near the edge, corresponding to the peak of the bootstrap current, have been found to have infernal-like features (Zheng, Kotschenreuther & Valanju Reference Zheng, Kotschenreuther and Valanju2013a
,Reference Zheng, Kotschenreuther and Valanju
b
). Indeed under these conditions, i.e. large pressure gradients and
$q$
near the edge, corresponding to the peak of the bootstrap current, have been found to have infernal-like features (Zheng, Kotschenreuther & Valanju Reference Zheng, Kotschenreuther and Valanju2013a
,Reference Zheng, Kotschenreuther and Valanju
b
). Indeed under these conditions, i.e. large pressure gradients and
![]() $q$
flat over and extended region, it is likely that infernal type instabilities develop. These instabilities are characterised by a toroidicity induced coupling between neighbouring Fourier harmonics, i.e. a dominant
$q$
flat over and extended region, it is likely that infernal type instabilities develop. These instabilities are characterised by a toroidicity induced coupling between neighbouring Fourier harmonics, i.e. a dominant
![]() $m_{0}$
mode is coupled with its sidebands
$m_{0}$
mode is coupled with its sidebands
![]() $m_{0}\pm 1$
. Three-dimensional free boundary MHD equilibria simulations of Joint European Torus (JET) and Tokamak à Configuration Variable (TCV)-like plasmas, in which a large edge bootstrap current flattens the safety factor, recovered saturated ideal kink/peeling structures (Cooper et al.
Reference Cooper, Graves, Duval, Porte, Reimerdes, Sauter and Tran2015, Reference Cooper, Brunetti, Duval, Faustin, Graves, Kleiner, Patten, Pfefferlé, Porte and Raghunathan2016a
,Reference Cooper, Graves, Duval, Sauter, Faustin, Kleiner, Lanthaler, Patten, Raghunathan and Tran
b
). The computed equilibrium state is characterised by a distorted boundary with a dominant
$m_{0}\pm 1$
. Three-dimensional free boundary MHD equilibria simulations of Joint European Torus (JET) and Tokamak à Configuration Variable (TCV)-like plasmas, in which a large edge bootstrap current flattens the safety factor, recovered saturated ideal kink/peeling structures (Cooper et al.
Reference Cooper, Graves, Duval, Porte, Reimerdes, Sauter and Tran2015, Reference Cooper, Brunetti, Duval, Faustin, Graves, Kleiner, Patten, Pfefferlé, Porte and Raghunathan2016a
,Reference Cooper, Graves, Duval, Sauter, Faustin, Kleiner, Lanthaler, Patten, Raghunathan and Tran
b
). The computed equilibrium state is characterised by a distorted boundary with a dominant
![]() $n=1$
Fourier component where the corrugation is driven mainly by non-axisymmetric components of the parallel current density.
$n=1$
Fourier component where the corrugation is driven mainly by non-axisymmetric components of the parallel current density.
Thus the main aim of this work is to study analytically the stability properties against infernal modes of MHD equilibria which present a local flattening of the safety factor close to the plasma boundary associated with large pressure gradients. We follow the analysis presented in Brunetti et al. (Reference Brunetti, Graves, Lazzaro, Mariani, Nowak, Cooper and Wahlberg2018) bringing out the work more deeply, and more importantly, looking at extensions which include toroidal mode number analysis and resistive walls. Also we extend the results previously obtained in Brunetti et al. (Reference Brunetti, Graves, Lazzaro, Mariani, Nowak, Cooper and Wahlberg2018) to different types of more realistic profiles (
![]() $q$
etc.). We assume a vacuum region separating the plasma and the metallic wall. The analysis of the perturbation is split into various regions, each treated separately. The eigensolutions for the Fourier modes in each region are matched with the appropriate choice of the plasma–vacuum and vacuum–wall jump interface conditions. This eventually yields the dispersion relation.
$q$
etc.). We assume a vacuum region separating the plasma and the metallic wall. The analysis of the perturbation is split into various regions, each treated separately. The eigensolutions for the Fourier modes in each region are matched with the appropriate choice of the plasma–vacuum and vacuum–wall jump interface conditions. This eventually yields the dispersion relation.
The paper is organised as follows: § 2 describes the geometry and the physical model employed for the plasma modelling. The infernal modes equations are introduced and a discussion on their validity in application to our problem is given. In § 3 the eigensolutions for coupled Fourier harmonics are solved for a particular choice of the safety factor profile and their logarithmic jumps across the transition point between high and low-shear regions are evaluated. In § 4 we solve for the vacuum perturbation and apply the appropriate boundary conditions at the plasma edge and metallic wall interfaces. The solution of the equation for the main eigenmode
![]() $m_{0}$
and the matching procedure with the high-shear region eigensolutions is presented in § 5 where two classes of equilibrium profiles for temperature and mass density are considered. The dispersion relation is eventually derived and discussed in § 6 with two different wall boundary conditions. Finally the findings of this work and future outlook are summarised in § 7. The appendices include a description of inertial corrections and residual coupling effects at the resonant surface of the
$m_{0}$
and the matching procedure with the high-shear region eigensolutions is presented in § 5 where two classes of equilibrium profiles for temperature and mass density are considered. The dispersion relation is eventually derived and discussed in § 6 with two different wall boundary conditions. Finally the findings of this work and future outlook are summarised in § 7. The appendices include a description of inertial corrections and residual coupling effects at the resonant surface of the
![]() $m_{0}-1$
harmonic.
$m_{0}-1$
harmonic.
2 Physical model
We consider a large aspect ratio tokamak of major and minor radii
![]() $R_{0}$
and
$R_{0}$
and
![]() $a$
respectively (
$a$
respectively (
![]() $\unicode[STIX]{x1D700}=a/R_{0}\ll 1$
) with shifted circular toroidal surfaces. The vacuum region extends for
$\unicode[STIX]{x1D700}=a/R_{0}\ll 1$
) with shifted circular toroidal surfaces. The vacuum region extends for
![]() $a<r<b$
and for
$a<r<b$
and for
![]() $r>b+d$
and a metallic wall of thickness
$r>b+d$
and a metallic wall of thickness
![]() $d$
is located at
$d$
is located at
![]() $b<r<b+d$
. The equilibrium assumes a strong toroidal field (
$b<r<b+d$
. The equilibrium assumes a strong toroidal field (
![]() $B_{T}$
) and a smaller poloidal field (
$B_{T}$
) and a smaller poloidal field (
![]() $B_{P}$
), i.e.
$B_{P}$
), i.e.
![]() $B_{P}/B_{T}\sim \text{O}(\unicode[STIX]{x1D700})$
with
$B_{P}/B_{T}\sim \text{O}(\unicode[STIX]{x1D700})$
with
![]() $\unicode[STIX]{x1D6FD}\sim \text{O}(\unicode[STIX]{x1D700}^{2})$
(here
$\unicode[STIX]{x1D6FD}\sim \text{O}(\unicode[STIX]{x1D700}^{2})$
(here
![]() $\unicode[STIX]{x1D6FD}=p_{0}/B_{T}^{2}$
where
$\unicode[STIX]{x1D6FD}=p_{0}/B_{T}^{2}$
where
![]() $p_{0}$
is the equilibrium pressure). We use a right-handed straight field line coordinate system
$p_{0}$
is the equilibrium pressure). We use a right-handed straight field line coordinate system
![]() $(r,\unicode[STIX]{x1D717},\unicode[STIX]{x1D711})$
where
$(r,\unicode[STIX]{x1D717},\unicode[STIX]{x1D711})$
where
![]() $r$
is a flux label with the dimensions of length,
$r$
is a flux label with the dimensions of length,
![]() $\unicode[STIX]{x1D717}$
and
$\unicode[STIX]{x1D717}$
and
![]() $\unicode[STIX]{x1D711}$
are the poloidal-like (counter-clockwise) and toroidal angles respectively. The contravariant and covariant basis vectors are denoted hereafter by
$\unicode[STIX]{x1D711}$
are the poloidal-like (counter-clockwise) and toroidal angles respectively. The contravariant and covariant basis vectors are denoted hereafter by
![]() $\unicode[STIX]{x1D735}C^{i}$
and
$\unicode[STIX]{x1D735}C^{i}$
and
![]() $\boldsymbol{e}_{C^{i}}$
respectively, with
$\boldsymbol{e}_{C^{i}}$
respectively, with
![]() $C^{i}=(r,\unicode[STIX]{x1D717},\unicode[STIX]{x1D711})$
.
$C^{i}=(r,\unicode[STIX]{x1D717},\unicode[STIX]{x1D711})$
.
The magnetic field in the plasma is represented in terms of flux functions (D’haeseleer et al. Reference D’haeseleer, Hitchon, Callen and Shohet1991):
The equilibrium fluxes, denoted with
![]() $\unicode[STIX]{x1D713}_{0}$
and
$\unicode[STIX]{x1D713}_{0}$
and
![]() $f_{0}$
, depend only on
$f_{0}$
, depend only on
![]() $r$
, and
$r$
, and
![]() $q=f_{0}^{\prime }/\unicode[STIX]{x1D713}_{0}^{\prime }$
with
$q=f_{0}^{\prime }/\unicode[STIX]{x1D713}_{0}^{\prime }$
with
![]() $f_{0}^{\prime }\approx B_{0}r$
which follows from
$f_{0}^{\prime }\approx B_{0}r$
which follows from
![]() $B_{T}\approx R_{0}B_{0}/R$
(Wesson Reference Wesson2011) (
$B_{T}\approx R_{0}B_{0}/R$
(Wesson Reference Wesson2011) (
![]() $B_{0}$
is the magnetic field strength on the axis and the prime denotes the derivative with respect to the radial variable). Normalising
$B_{0}$
is the magnetic field strength on the axis and the prime denotes the derivative with respect to the radial variable). Normalising
![]() $\unicode[STIX]{x1D707}_{0}=1$
(
$\unicode[STIX]{x1D707}_{0}=1$
(
![]() $\unicode[STIX]{x1D707}_{0}$
is the vacuum permeability), from Ampére’s law
$\unicode[STIX]{x1D707}_{0}$
is the vacuum permeability), from Ampére’s law
![]() $\boldsymbol{J}=\unicode[STIX]{x1D735}\times \boldsymbol{B}$
where
$\boldsymbol{J}=\unicode[STIX]{x1D735}\times \boldsymbol{B}$
where
![]() $\boldsymbol{J}$
is the current density, we have
$\boldsymbol{J}$
is the current density, we have
![]() $J_{0}=J_{0}^{\unicode[STIX]{x1D711}}/B_{0}^{\unicode[STIX]{x1D711}}=1/R_{0}[(r\unicode[STIX]{x1D707})^{\prime }+\unicode[STIX]{x1D707}]$
and
$J_{0}=J_{0}^{\unicode[STIX]{x1D711}}/B_{0}^{\unicode[STIX]{x1D711}}=1/R_{0}[(r\unicode[STIX]{x1D707})^{\prime }+\unicode[STIX]{x1D707}]$
and
![]() $J_{0}^{\prime }=1/(mR_{0})[(r^{2}k_{||,m})^{\prime }/r]^{\prime }$
(Hazeltine & Meiss Reference Hazeltine and Meiss1992), where
$J_{0}^{\prime }=1/(mR_{0})[(r^{2}k_{||,m})^{\prime }/r]^{\prime }$
(Hazeltine & Meiss Reference Hazeltine and Meiss1992), where
![]() $\unicode[STIX]{x1D707}=1/q$
and
$\unicode[STIX]{x1D707}=1/q$
and
![]() $k_{||,m}=m\unicode[STIX]{x1D707}-n$
with
$k_{||,m}=m\unicode[STIX]{x1D707}-n$
with
![]() $m$
and
$m$
and
![]() $n$
integers.
$n$
integers.
Our stability analysis is based on the following ideal MHD equations (Hazeltine & Meiss Reference Hazeltine and Meiss1992):
where
![]() $\unicode[STIX]{x1D6E4}$
is the adiabatic index,
$\unicode[STIX]{x1D6E4}$
is the adiabatic index,
![]() $\boldsymbol{E}$
is the electric field and
$\boldsymbol{E}$
is the electric field and
![]() $\boldsymbol{v}$
is the plasma MHD velocity. It is convenient to write
$\boldsymbol{v}$
is the plasma MHD velocity. It is convenient to write
![]() $\boldsymbol{v}=\unicode[STIX]{x2202}\unicode[STIX]{x1D743}/\unicode[STIX]{x2202}t$
where
$\boldsymbol{v}=\unicode[STIX]{x2202}\unicode[STIX]{x1D743}/\unicode[STIX]{x2202}t$
where
![]() $\unicode[STIX]{x1D743}$
is the Lagrangian perturbed fluid displacement. Finally
$\unicode[STIX]{x1D743}$
is the Lagrangian perturbed fluid displacement. Finally
![]() $\unicode[STIX]{x1D70C}$
is the mass density and
$\unicode[STIX]{x1D70C}$
is the mass density and
![]() $p$
the plasma pressure. We stress the point that we consider an ideal plasma so that the development of tearing type instabilities is prevented. By means of (2.3) we have:
$p$
the plasma pressure. We stress the point that we consider an ideal plasma so that the development of tearing type instabilities is prevented. By means of (2.3) we have:
where
![]() $\tilde{\boldsymbol{B}}$
is the perturbed magnetic field and
$\tilde{\boldsymbol{B}}$
is the perturbed magnetic field and
![]() $\boldsymbol{B}_{0}$
the equilibrium magnetic field. From now on equilibrium quantities will be denoted with the subscript 0 and perturbed quantities have a dependence on time and angular variables of the type
$\boldsymbol{B}_{0}$
the equilibrium magnetic field. From now on equilibrium quantities will be denoted with the subscript 0 and perturbed quantities have a dependence on time and angular variables of the type
![]() $\exp [\text{i}(m\unicode[STIX]{x1D717}-n\unicode[STIX]{x1D711})+\unicode[STIX]{x1D6FE}t]$
.
$\exp [\text{i}(m\unicode[STIX]{x1D717}-n\unicode[STIX]{x1D711})+\unicode[STIX]{x1D6FE}t]$
.
For our analysis we choose a safety factor which has a local edge flattening as shown in figure 1. The gap between the safety factor and the resonance
![]() $m_{0}/n$
is denoted by
$m_{0}/n$
is denoted by
![]() $\unicode[STIX]{x1D6FF}q$
, i.e.
$\unicode[STIX]{x1D6FF}q$
, i.e.
![]() $\unicode[STIX]{x1D6FF}q=q-m_{0}/n$
(
$\unicode[STIX]{x1D6FF}q=q-m_{0}/n$
(
![]() $\unicode[STIX]{x1D6FF}q$
can be either positive or negative) with
$\unicode[STIX]{x1D6FF}q$
can be either positive or negative) with
![]() $\unicode[STIX]{x1D6FF}q$
small. It is implicitly assumed that
$\unicode[STIX]{x1D6FF}q$
small. It is implicitly assumed that
![]() $m_{0}>1$
. In a more realistic geometry with separatrix the safety factor grows to large values, although in a narrow region much smaller than the expected radial extension of the mode. This particular case is outside of the scope of the present work. Nevertheless, motivated by Medvedev et al. (Reference Medvedev, Martynov, Martin, Sauter and Villard2006), Zheng et al. (Reference Zheng, Kotschenreuther and Valanju2013a
,Reference Zheng, Kotschenreuther and Valanju
b
), we expect that the main physical ingredients for the development of an edge infernal type MHD instability are captured. According to Turnbull & Troyon (Reference Turnbull and Troyon1989) we assume that the ratio
$m_{0}>1$
. In a more realistic geometry with separatrix the safety factor grows to large values, although in a narrow region much smaller than the expected radial extension of the mode. This particular case is outside of the scope of the present work. Nevertheless, motivated by Medvedev et al. (Reference Medvedev, Martynov, Martin, Sauter and Villard2006), Zheng et al. (Reference Zheng, Kotschenreuther and Valanju2013a
,Reference Zheng, Kotschenreuther and Valanju
b
), we expect that the main physical ingredients for the development of an edge infernal type MHD instability are captured. According to Turnbull & Troyon (Reference Turnbull and Troyon1989) we assume that the ratio
![]() $q_{a}/q_{0}$
is sufficiently large (
$q_{a}/q_{0}$
is sufficiently large (
![]() $q_{0}$
and
$q_{0}$
and
![]() $q_{a}$
are the values of the safety factor on the magnetic axis and at the edge respectively) in order to be stable against low-
$q_{a}$
are the values of the safety factor on the magnetic axis and at the edge respectively) in order to be stable against low-
![]() $n$
external kink modes.
$n$
external kink modes.

Figure 1. Model safety factor with the vacuum region extending from
![]() $a$
to
$a$
to
![]() $b$
. In the edge low-shear region (
$b$
. In the edge low-shear region (
![]() $r_{\ast }<r<a$
) the
$r_{\ast }<r<a$
) the
![]() $q$
profile is close to
$q$
profile is close to
![]() $m_{0}/n$
. The position of the
$m_{0}/n$
. The position of the
![]() $(m_{0}-1)/n$
resonant surface is highlighted.
$(m_{0}-1)/n$
resonant surface is highlighted.
According to figure 1, we refer to the region which extends from the magnetic axis to
![]() $r=r_{\ast }<a$
as the sheared region where the magnetic shear is large (
$r=r_{\ast }<a$
as the sheared region where the magnetic shear is large (
![]() $q^{\prime }\sim \text{O}(1)$
) and the pressure gradient sufficiently small. Here mode coupling is prevented and different Fourier harmonics behave independently according to (Mikhailovskii Reference Mikhailovskii1998; Brunetti et al.
Reference Brunetti, Graves, Cooper and Wahlberg2014):
$q^{\prime }\sim \text{O}(1)$
) and the pressure gradient sufficiently small. Here mode coupling is prevented and different Fourier harmonics behave independently according to (Mikhailovskii Reference Mikhailovskii1998; Brunetti et al.
Reference Brunetti, Graves, Cooper and Wahlberg2014):
It will be shown in § 4 that also the vacuum magnetic perturbation is described by (2.7). Indeed in the vacuum the safety factor is expected to grow as
![]() $r^{2}$
so that we can regard also this region as a sheared region.
$r^{2}$
so that we can regard also this region as a sheared region.
The low-shear region extends from
![]() $r_{\ast }$
to the plasma edge
$r_{\ast }$
to the plasma edge
![]() $r=a$
. Here the safety factor is almost flat and close to
$r=a$
. Here the safety factor is almost flat and close to
![]() $m_{0}/n$
. In this region pressure gradients and field line bending weakening allow for mode coupling between neighbouring poloidal Fourier harmonics (Hastie & Hender Reference Hastie and Hender1988; Waelbroeck & Hazeltine Reference Waelbroeck and Hazeltine1988; Gimblett, Hastie & Hender Reference Gimblett, Hastie and Hender1996; Brunetti et al.
Reference Brunetti, Graves, Cooper and Wahlberg2014). The presence of three Fourier modes with mode numbers
$m_{0}/n$
. In this region pressure gradients and field line bending weakening allow for mode coupling between neighbouring poloidal Fourier harmonics (Hastie & Hender Reference Hastie and Hender1988; Waelbroeck & Hazeltine Reference Waelbroeck and Hazeltine1988; Gimblett, Hastie & Hender Reference Gimblett, Hastie and Hender1996; Brunetti et al.
Reference Brunetti, Graves, Cooper and Wahlberg2014). The presence of three Fourier modes with mode numbers
![]() $(m_{0},n),(m_{0}\pm 1,n)$
is assumed whose relative amplitude is
$(m_{0},n),(m_{0}\pm 1,n)$
is assumed whose relative amplitude is
![]() $X_{m_{0}\pm 1,n}\sim \text{O}(\unicode[STIX]{x1D700})X_{m_{0},n}$
, where
$X_{m_{0}\pm 1,n}\sim \text{O}(\unicode[STIX]{x1D700})X_{m_{0},n}$
, where
![]() $X=\unicode[STIX]{x1D743}\boldsymbol{\cdot }\unicode[STIX]{x1D735}r$
. For sake of simplicity hereafter we will drop the subscript
$X=\unicode[STIX]{x1D743}\boldsymbol{\cdot }\unicode[STIX]{x1D735}r$
. For sake of simplicity hereafter we will drop the subscript
![]() $n$
and we introduce the notation
$n$
and we introduce the notation
![]() $X_{\pm }=X_{m_{0}\pm 1,n}$
. The equations describing the perturbation are (Hastie & Hender Reference Hastie and Hender1988; Waelbroeck & Hazeltine Reference Waelbroeck and Hazeltine1988; Gimblett et al.
Reference Gimblett, Hastie and Hender1996; Wahlberg, Graves & Chapman Reference Wahlberg, Graves and Chapman2013; Brunetti et al.
Reference Brunetti, Graves, Cooper and Wahlberg2014):
$X_{\pm }=X_{m_{0}\pm 1,n}$
. The equations describing the perturbation are (Hastie & Hender Reference Hastie and Hender1988; Waelbroeck & Hazeltine Reference Waelbroeck and Hazeltine1988; Gimblett et al.
Reference Gimblett, Hastie and Hender1996; Wahlberg, Graves & Chapman Reference Wahlberg, Graves and Chapman2013; Brunetti et al.
Reference Brunetti, Graves, Cooper and Wahlberg2014):
 $$\begin{eqnarray}\displaystyle & \displaystyle {\displaystyle \frac{\text{d}}{\text{d}r}}\left[r^{3}Q{\displaystyle \frac{\text{d}X_{m_{0}}}{\text{d}r}}\right]+r\left[(1-m_{0}^{2})Q+r\left({\displaystyle \frac{A_{2}}{n^{2}}}\right)^{\prime }-{\displaystyle \frac{\unicode[STIX]{x1D6FC}^{2}}{2}}+{\displaystyle \frac{\unicode[STIX]{x1D6FC}r}{R_{0}}}\left({\displaystyle \frac{1}{q^{2}}}-1\right)\right]X_{m_{0}} & \displaystyle \nonumber\\ \displaystyle & \displaystyle +{\displaystyle \frac{\unicode[STIX]{x1D6FC}}{2}}\left[{\displaystyle \frac{r^{-m_{0}}}{1+m_{0}}}(r^{2+m_{0}}X_{+})^{\prime }+{\displaystyle \frac{r^{m_{0}}}{1-m_{0}}}(r^{2-m_{0}}X_{-})^{\prime }\right]=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\displaystyle \frac{\text{d}}{\text{d}r}}\left[r^{3}Q{\displaystyle \frac{\text{d}X_{m_{0}}}{\text{d}r}}\right]+r\left[(1-m_{0}^{2})Q+r\left({\displaystyle \frac{A_{2}}{n^{2}}}\right)^{\prime }-{\displaystyle \frac{\unicode[STIX]{x1D6FC}^{2}}{2}}+{\displaystyle \frac{\unicode[STIX]{x1D6FC}r}{R_{0}}}\left({\displaystyle \frac{1}{q^{2}}}-1\right)\right]X_{m_{0}} & \displaystyle \nonumber\\ \displaystyle & \displaystyle +{\displaystyle \frac{\unicode[STIX]{x1D6FC}}{2}}\left[{\displaystyle \frac{r^{-m_{0}}}{1+m_{0}}}(r^{2+m_{0}}X_{+})^{\prime }+{\displaystyle \frac{r^{m_{0}}}{1-m_{0}}}(r^{2-m_{0}}X_{-})^{\prime }\right]=0, & \displaystyle\end{eqnarray}$$
with
![]() $Q=(\unicode[STIX]{x1D6FF}q/q)^{2}+A_{1}/n^{2}$
,
$Q=(\unicode[STIX]{x1D6FF}q/q)^{2}+A_{1}/n^{2}$
,
![]() $\unicode[STIX]{x1D714}_{A}=B_{0}/(R_{0}\sqrt{\unicode[STIX]{x1D70C}})$
and
$\unicode[STIX]{x1D714}_{A}=B_{0}/(R_{0}\sqrt{\unicode[STIX]{x1D70C}})$
and
![]() $\unicode[STIX]{x1D6FC}=-(2R_{0}p_{0}^{\prime }q^{2})/B_{0}^{2}$
. Equilibrium mass density gradients are allowed since they play an important role in the determination of the pressure gradients in the narrow edge region where the perturbation we are interested in is localised. In the limit
$\unicode[STIX]{x1D6FC}=-(2R_{0}p_{0}^{\prime }q^{2})/B_{0}^{2}$
. Equilibrium mass density gradients are allowed since they play an important role in the determination of the pressure gradients in the narrow edge region where the perturbation we are interested in is localised. In the limit
![]() $\unicode[STIX]{x1D6FE}/[\unicode[STIX]{x1D6E4}p_{0}/(\unicode[STIX]{x1D70C}_{0}R_{0}^{2})]\ll 1$
we approximate (Wahlberg et al.
Reference Wahlberg, Graves and Chapman2013)
$\unicode[STIX]{x1D6FE}/[\unicode[STIX]{x1D6E4}p_{0}/(\unicode[STIX]{x1D70C}_{0}R_{0}^{2})]\ll 1$
we approximate (Wahlberg et al.
Reference Wahlberg, Graves and Chapman2013)
![]() $A_{1}\simeq (\unicode[STIX]{x1D70C}_{0}\unicode[STIX]{x1D6FE}^{2})/(\bar{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D714}_{A}^{2})[1+2q^{2}]$
and
$A_{1}\simeq (\unicode[STIX]{x1D70C}_{0}\unicode[STIX]{x1D6FE}^{2})/(\bar{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D714}_{A}^{2})[1+2q^{2}]$
and
![]() $A_{2}\approx A_{1}$
(
$A_{2}\approx A_{1}$
(
![]() $\bar{\unicode[STIX]{x1D70C}}$
is the value of the mass density on the magnetic axis).
$\bar{\unicode[STIX]{x1D70C}}$
is the value of the mass density on the magnetic axis).
Equations (2.8) and (2.9) have been derived for
![]() $\unicode[STIX]{x1D6FD}\sim \unicode[STIX]{x1D700}^{2}$
. Then the following question arises: are they applicable when the pressure gradient increases, i.e. when
$\unicode[STIX]{x1D6FD}\sim \unicode[STIX]{x1D700}^{2}$
. Then the following question arises: are they applicable when the pressure gradient increases, i.e. when
![]() $\unicode[STIX]{x1D6FC}\sim 1$
? We point out that from (2.8), the requirement that the inertial term is of the same order as the coupling term gives
$\unicode[STIX]{x1D6FC}\sim 1$
? We point out that from (2.8), the requirement that the inertial term is of the same order as the coupling term gives
![]() $Q\sim (\unicode[STIX]{x1D6FC}\unicode[STIX]{x0394}r/a)^{2}$
where
$Q\sim (\unicode[STIX]{x1D6FC}\unicode[STIX]{x0394}r/a)^{2}$
where
![]() $\unicode[STIX]{x0394}r$
is the width of the low-shear region. In the following analysis we assume that
$\unicode[STIX]{x0394}r$
is the width of the low-shear region. In the following analysis we assume that
![]() $Q\sim \unicode[STIX]{x1D700}^{2}$
. If
$Q\sim \unicode[STIX]{x1D700}^{2}$
. If
![]() $\unicode[STIX]{x1D6FC}\sim 1$
and the pressure gradient is localised within a narrow region, the assumption of concentric circular magnetic surfaces still holds (Greene & Chance Reference Greene and Chance1981; Connor, Ham & Hastie Reference Connor, Ham and Hastie2016). From the equation for the Shafranov shift
$\unicode[STIX]{x1D6FC}\sim 1$
and the pressure gradient is localised within a narrow region, the assumption of concentric circular magnetic surfaces still holds (Greene & Chance Reference Greene and Chance1981; Connor, Ham & Hastie Reference Connor, Ham and Hastie2016). From the equation for the Shafranov shift
![]() $\unicode[STIX]{x1D6E5}_{s}$
(assumed of order
$\unicode[STIX]{x1D6E5}_{s}$
(assumed of order
![]() $\unicode[STIX]{x1D700}$
):
$\unicode[STIX]{x1D700}$
):
we approximate
![]() $r\unicode[STIX]{x1D6E5}_{s}^{\prime \prime }\approx \unicode[STIX]{x1D6FC}$
and
$r\unicode[STIX]{x1D6E5}_{s}^{\prime \prime }\approx \unicode[STIX]{x1D6FC}$
and
![]() $T_{0}^{\prime }=-p_{0}^{\prime }R_{0}/B_{0}\sim \unicode[STIX]{x1D6FC}$
(
$T_{0}^{\prime }=-p_{0}^{\prime }R_{0}/B_{0}\sim \unicode[STIX]{x1D6FC}$
(
![]() $T_{0}=B_{0,\unicode[STIX]{x1D711}}$
being the toroidal covariant component of the equilibrium magnetic field (Greene & Weimer Reference Greene and Weimer1971; Connor et al.
Reference Connor, Ham and Hastie2016)).
$T_{0}=B_{0,\unicode[STIX]{x1D711}}$
being the toroidal covariant component of the equilibrium magnetic field (Greene & Weimer Reference Greene and Weimer1971; Connor et al.
Reference Connor, Ham and Hastie2016)).
Neglecting effects linear with respect to the magnetic shear (i.e. assume a flat
![]() $q$
) the elements of the metric tensor in our straight field line coordinate system are evaluated up to order
$q$
) the elements of the metric tensor in our straight field line coordinate system are evaluated up to order
![]() $\unicode[STIX]{x1D700}$
giving:
$\unicode[STIX]{x1D700}$
giving:
where the ratio
![]() $g_{\unicode[STIX]{x1D711}\unicode[STIX]{x1D711}}/\sqrt{g}$
depends only on the flux label
$g_{\unicode[STIX]{x1D711}\unicode[STIX]{x1D711}}/\sqrt{g}$
depends only on the flux label
![]() $r$
having used (2.10) and
$r$
having used (2.10) and
![]() $\langle R^{2}\rangle ^{\prime }\approx -R_{0}\unicode[STIX]{x1D6FC}$
, where
$\langle R^{2}\rangle ^{\prime }\approx -R_{0}\unicode[STIX]{x1D6FC}$
, where
![]() $\langle \boldsymbol{\cdot }\,\rangle :=\,1/2\unicode[STIX]{x03C0}\int _{0}^{2\unicode[STIX]{x03C0}}(\boldsymbol{\cdot })\,\text{d}\unicode[STIX]{x1D717}$
. We see that
$\langle \boldsymbol{\cdot }\,\rangle :=\,1/2\unicode[STIX]{x03C0}\int _{0}^{2\unicode[STIX]{x03C0}}(\boldsymbol{\cdot })\,\text{d}\unicode[STIX]{x1D717}$
. We see that
![]() $g_{rr}$
and
$g_{rr}$
and
![]() $g_{r\unicode[STIX]{x1D717}}$
are modified compared to their standard low
$g_{r\unicode[STIX]{x1D717}}$
are modified compared to their standard low
![]() $\unicode[STIX]{x1D6FD}$
expressions (Lazzaro & Zanca Reference Lazzaro and Zanca2003; Brunetti et al.
Reference Brunetti, Graves, Cooper and Wahlberg2014). The latter are recovered by allowing
$\unicode[STIX]{x1D6FD}$
expressions (Lazzaro & Zanca Reference Lazzaro and Zanca2003; Brunetti et al.
Reference Brunetti, Graves, Cooper and Wahlberg2014). The latter are recovered by allowing
![]() $\unicode[STIX]{x1D6FC}$
to become small. Note that ellipticity and triangularity have not been included since they do not play a role in the coupling mechanism between
$\unicode[STIX]{x1D6FC}$
to become small. Note that ellipticity and triangularity have not been included since they do not play a role in the coupling mechanism between
![]() $\pm 1$
neighbouring sidebands. This is because of the elongation and triangularity angular dependencies of the type
$\pm 1$
neighbouring sidebands. This is because of the elongation and triangularity angular dependencies of the type
![]() $\cos 2\unicode[STIX]{x1D717}$
and
$\cos 2\unicode[STIX]{x1D717}$
and
![]() $\sin 2\unicode[STIX]{x1D717}$
respectively (Connor et al.
Reference Connor, Ham and Hastie2016).
$\sin 2\unicode[STIX]{x1D717}$
respectively (Connor et al.
Reference Connor, Ham and Hastie2016).
For
![]() $\unicode[STIX]{x1D6FC}\lesssim 1$
we approximate
$\unicode[STIX]{x1D6FC}\lesssim 1$
we approximate
![]() $g_{rr}\simeq 1$
and at leading order the set of the equations describing the perturbation is still given by (2.8) and (2.9). Conversely, assuming that
$g_{rr}\simeq 1$
and at leading order the set of the equations describing the perturbation is still given by (2.8) and (2.9). Conversely, assuming that
![]() $\unicode[STIX]{x1D6FC}\gtrsim 1$
in a narrow region of width
$\unicode[STIX]{x1D6FC}\gtrsim 1$
in a narrow region of width
![]() $\unicode[STIX]{x0394}r$
, we introduce the following orderings:
$\unicode[STIX]{x0394}r$
, we introduce the following orderings:
By means of (2.15) and employing the large
![]() $\unicode[STIX]{x1D6FC}$
metric tensor, at leading order we can derive the following coupled equations (we approximate
$\unicode[STIX]{x1D6FC}$
metric tensor, at leading order we can derive the following coupled equations (we approximate
![]() $r_{\ast }\sim a$
):
$r_{\ast }\sim a$
):
The two simpler equations above can be used as an alternative to (2.8) and (2.9) in order to make analytically treatable more complex/realistic profiles. This will be discussed in § 5.2. We arrive to the same set of equations also when we have
![]() $1/m\sim \unicode[STIX]{x0394}r/r\sim \unicode[STIX]{x1D700}^{1/2}$
(in this case
$1/m\sim \unicode[STIX]{x0394}r/r\sim \unicode[STIX]{x1D700}^{1/2}$
(in this case
![]() $X_{\pm }/X_{m_{0}}\sim \unicode[STIX]{x1D700}^{1/2}$
). Pushing further the ordering of
$X_{\pm }/X_{m_{0}}\sim \unicode[STIX]{x1D700}^{1/2}$
). Pushing further the ordering of
![]() $m$
, i.e.
$m$
, i.e.
![]() $1/m\sim \unicode[STIX]{x1D700}$
, we enter in a ballooning-like configuration, where the weight of all the harmonics is approximately the same. This problem is not addressed and is beyond the scope of the paper.
$1/m\sim \unicode[STIX]{x1D700}$
, we enter in a ballooning-like configuration, where the weight of all the harmonics is approximately the same. This problem is not addressed and is beyond the scope of the paper.
Therefore equations (2.7), (2.8) and (2.9) (or alternatively (2.16) and (2.17)) form the basis for the analysis developed in the next sections. The solutions to this set of equations must fulfil the boundary conditions imposed at the plasma-‘outer world’ interface at
![]() $r=a$
. These boundary conditions are obtained by solving the perturbation in the vacuum region. Hence the solution to the problem proceeds as follows: first the equations for the perturbations are solved in the sheared and vacuum regions (with the appropriate boundary conditions at the magnetic axis and at the external metallic shell). Then equations (2.8) and (2.9) (or (2.16) and (2.17)) are solved in the low-shear region. Matching of the eigensolutions across the transition points yields eventually the dispersion relation.
$r=a$
. These boundary conditions are obtained by solving the perturbation in the vacuum region. Hence the solution to the problem proceeds as follows: first the equations for the perturbations are solved in the sheared and vacuum regions (with the appropriate boundary conditions at the magnetic axis and at the external metallic shell). Then equations (2.8) and (2.9) (or (2.16) and (2.17)) are solved in the low-shear region. Matching of the eigensolutions across the transition points yields eventually the dispersion relation.
3 Sheared region eigenfunctions
The aim of this section is to derive the shape of the main mode
![]() $m_{0}$
and the logarithmic derivative of the neighbouring
$m_{0}$
and the logarithmic derivative of the neighbouring
![]() $X_{\pm }$
. These quantities are required for the derivation of the dispersion relation when matching of the eigenfunctions at
$X_{\pm }$
. These quantities are required for the derivation of the dispersion relation when matching of the eigenfunctions at
![]() $r_{\ast }$
is required.
$r_{\ast }$
is required.
The profile of the rotational transform in
![]() $0<r<r_{\ast }$
is taken of the form (Mikhailovskii Reference Mikhailovskii1998):
$0<r<r_{\ast }$
is taken of the form (Mikhailovskii Reference Mikhailovskii1998):
where
![]() $r_{s}$
is the position of the resonant surface of the mode
$r_{s}$
is the position of the resonant surface of the mode
![]() $(m_{0}-1,n)$
(cf. figure 1). This choice for the safety factor allows the eigenproblem to be analytically solvable in terms of the hypergeometric equation. By requiring that
$(m_{0}-1,n)$
(cf. figure 1). This choice for the safety factor allows the eigenproblem to be analytically solvable in terms of the hypergeometric equation. By requiring that
![]() $\unicode[STIX]{x1D707}(r_{\ast })\approx n/m_{0}$
we obtain
$\unicode[STIX]{x1D707}(r_{\ast })\approx n/m_{0}$
we obtain
![]() $S=(n/m_{0})/[(r_{\ast }/r_{s})^{\unicode[STIX]{x1D706}}-1]$
. Note that in this approximation
$S=(n/m_{0})/[(r_{\ast }/r_{s})^{\unicode[STIX]{x1D706}}-1]$
. Note that in this approximation
![]() $\unicode[STIX]{x1D6FF}q$
corrections appearing in the logarithmic derivatives of the eigenfunctions are neglected. We shall analyse each harmonic separately. Note that an alternative model (though less realistic) for the safety factor which provides simpler expressions for the logarithmic jumps of the
$\unicode[STIX]{x1D6FF}q$
corrections appearing in the logarithmic derivatives of the eigenfunctions are neglected. We shall analyse each harmonic separately. Note that an alternative model (though less realistic) for the safety factor which provides simpler expressions for the logarithmic jumps of the
![]() $m_{0}\pm 1$
sidebands has been used in Brunetti et al. (Reference Brunetti, Graves, Lazzaro, Mariani, Nowak, Cooper and Wahlberg2018).
$m_{0}\pm 1$
sidebands has been used in Brunetti et al. (Reference Brunetti, Graves, Lazzaro, Mariani, Nowak, Cooper and Wahlberg2018).
3.1 Main harmonic
 $m_{0}$
$m_{0}$
We multiply (2.7) by
![]() $X_{m_{0}}$
and integrate between 0 and
$X_{m_{0}}$
and integrate between 0 and
![]() $r_{\ast }$
(Hazeltine & Meiss Reference Hazeltine and Meiss1992; Mikhailovskii Reference Mikhailovskii1998) yielding:
$r_{\ast }$
(Hazeltine & Meiss Reference Hazeltine and Meiss1992; Mikhailovskii Reference Mikhailovskii1998) yielding:
where the boundary condition
![]() $X_{m_{0}}(0)=0$
is assumed. Since
$X_{m_{0}}(0)=0$
is assumed. Since
![]() $[r^{3}k_{||,m_{0}}^{2}X_{m}(\text{d}X_{m}/\text{d}r)]_{r_{\ast }}\sim k_{||,m_{0}}(r_{\ast })^{2}\ll 1$
(with the reasonable assumption that the derivatives are not diverging), we are left with an integral of positive terms which must be zero. The only possibility is that the function under the sign of integration is vanishing, this is:
$[r^{3}k_{||,m_{0}}^{2}X_{m}(\text{d}X_{m}/\text{d}r)]_{r_{\ast }}\sim k_{||,m_{0}}(r_{\ast })^{2}\ll 1$
(with the reasonable assumption that the derivatives are not diverging), we are left with an integral of positive terms which must be zero. The only possibility is that the function under the sign of integration is vanishing, this is:
This is in accordance with numerical calculations presented e.g. in Zheng et al. (Reference Zheng, Kotschenreuther and Valanju2013a
,Reference Zheng, Kotschenreuther and Valanju
b
). Note that the equation above still holds if the
![]() $q=m_{0}/n$
surface is crossed, viz.
$q=m_{0}/n$
surface is crossed, viz.
![]() $\unicode[STIX]{x1D6FF}q>0$
, if the resonant point of the main
$\unicode[STIX]{x1D6FF}q>0$
, if the resonant point of the main
![]() $m_{0}$
mode (to whom we refer with
$m_{0}$
mode (to whom we refer with
![]() $r_{m}$
) is not far from
$r_{m}$
) is not far from
![]() $r_{\ast }$
(i.e.
$r_{\ast }$
(i.e.
![]() $r_{m}\approx r_{\ast }$
) (Gimblett et al.
Reference Gimblett, Hastie and Hender1996).
$r_{m}\approx r_{\ast }$
) (Gimblett et al.
Reference Gimblett, Hastie and Hender1996).
3.2 Lower sideband (
 $m_{-}=m_{0}-1$
)
$m_{-}=m_{0}-1$
)
With the choice of the rotational transform given by (3.1), the expressions for the sidebands are readily obtained. Introducing the variable
![]() $z=(r/r_{s})^{\unicode[STIX]{x1D706}}$
, when
$z=(r/r_{s})^{\unicode[STIX]{x1D706}}$
, when
![]() $z<1$
, the solution of (2.7) for the lower sideband fulfilling the boundary condition on the magnetic axis (
$z<1$
, the solution of (2.7) for the lower sideband fulfilling the boundary condition on the magnetic axis (
![]() $X_{-}(0)<\infty$
) is (Kuvshinov & Mikhailovskii Reference Kuvshinov and Mikhailovskii1991; Mikhailovskii Reference Mikhailovskii1998; Brunetti et al.
Reference Brunetti, Graves, Cooper and Wahlberg2014):
$X_{-}(0)<\infty$
) is (Kuvshinov & Mikhailovskii Reference Kuvshinov and Mikhailovskii1991; Mikhailovskii Reference Mikhailovskii1998; Brunetti et al.
Reference Brunetti, Graves, Cooper and Wahlberg2014):
where
![]() $F$
is the hypergeometric function (see Abramowitz & Stegun Reference Abramowitz and Stegun1968, p. 555) and we defined
$F$
is the hypergeometric function (see Abramowitz & Stegun Reference Abramowitz and Stegun1968, p. 555) and we defined
![]() $\unicode[STIX]{x1D702}=(m_{-}-\bar{m}_{-})/\unicode[STIX]{x1D706}$
,
$\unicode[STIX]{x1D702}=(m_{-}-\bar{m}_{-})/\unicode[STIX]{x1D706}$
,
![]() $\unicode[STIX]{x1D701}=(m_{-}+\bar{m}_{-})/\unicode[STIX]{x1D706}$
,
$\unicode[STIX]{x1D701}=(m_{-}+\bar{m}_{-})/\unicode[STIX]{x1D706}$
,
![]() $\bar{m}_{-}=\sqrt{m_{-}^{2}+2\unicode[STIX]{x1D706}+\unicode[STIX]{x1D706}^{2}}$
. Conversely, when
$\bar{m}_{-}=\sqrt{m_{-}^{2}+2\unicode[STIX]{x1D706}+\unicode[STIX]{x1D706}^{2}}$
. Conversely, when
![]() $z>1$
, the solution of (3.3) reads (Kuvshinov & Mikhailovskii Reference Kuvshinov and Mikhailovskii1991; Mikhailovskii Reference Mikhailovskii1998; Brunetti et al.
Reference Brunetti, Graves, Cooper and Wahlberg2014):
$z>1$
, the solution of (3.3) reads (Kuvshinov & Mikhailovskii Reference Kuvshinov and Mikhailovskii1991; Mikhailovskii Reference Mikhailovskii1998; Brunetti et al.
Reference Brunetti, Graves, Cooper and Wahlberg2014):
where
![]() $A_{{>}}^{\ast }=-A_{{>}}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D701}\unicode[STIX]{x1D6E4}(-\unicode[STIX]{x1D702})\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D701}))/(\unicode[STIX]{x1D6E4}(1-\unicode[STIX]{x1D702}+\unicode[STIX]{x1D701}))$
and
$A_{{>}}^{\ast }=-A_{{>}}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D701}\unicode[STIX]{x1D6E4}(-\unicode[STIX]{x1D702})\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D701}))/(\unicode[STIX]{x1D6E4}(1-\unicode[STIX]{x1D702}+\unicode[STIX]{x1D701}))$
and
![]() $B_{{>}}^{\ast }=-B_{{>}}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D701}\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D702})\unicode[STIX]{x1D6E4}(-\unicode[STIX]{x1D701}))/$
$B_{{>}}^{\ast }=-B_{{>}}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D701}\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D702})\unicode[STIX]{x1D6E4}(-\unicode[STIX]{x1D701}))/$
![]() $(\unicode[STIX]{x1D6E4}(1+\unicode[STIX]{x1D702}-\unicode[STIX]{x1D701}))$
.
$(\unicode[STIX]{x1D6E4}(1+\unicode[STIX]{x1D702}-\unicode[STIX]{x1D701}))$
.
The asymptotic behaviour of (3.4) and (3.5) close to
![]() $r_{\ast }$
, depends on the ratio
$r_{\ast }$
, depends on the ratio
![]() $B_{{>}}/A_{{>}}$
. Neglecting for sake of simplicity inertial corrections,
$B_{{>}}/A_{{>}}$
. Neglecting for sake of simplicity inertial corrections,
![]() $B_{{>}}/A_{{>}}$
is found by imposing that for an ideal mode the displacement is finite at its own rational surface (modifications of the ratio
$B_{{>}}/A_{{>}}$
is found by imposing that for an ideal mode the displacement is finite at its own rational surface (modifications of the ratio
![]() $B_{{>}}/A_{{>}}$
due to inertial corrections or residual coupling effects are discussed in appendix A). Thus we immediately obtain
$B_{{>}}/A_{{>}}$
due to inertial corrections or residual coupling effects are discussed in appendix A). Thus we immediately obtain
![]() $B_{{>}}/A_{{>}}\rightarrow -1$
and
$B_{{>}}/A_{{>}}\rightarrow -1$
and
![]() $A_{{<}}=0$
.
$A_{{<}}=0$
.
In the limit
![]() $(r_{s}/r_{\ast })^{\unicode[STIX]{x1D706}}\ll 1$
, far from the resonant surface (
$(r_{s}/r_{\ast })^{\unicode[STIX]{x1D706}}\ll 1$
, far from the resonant surface (
![]() $z\gg 1$
), we have:
$z\gg 1$
), we have:
with
![]() $C_{0}=-(\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D702})\unicode[STIX]{x1D6E4}(-\unicode[STIX]{x1D701})\unicode[STIX]{x1D6E4}(1-\unicode[STIX]{x1D702}+\unicode[STIX]{x1D701}))/(\unicode[STIX]{x1D6E4}(-\unicode[STIX]{x1D702})\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D701})\unicode[STIX]{x1D6E4}(1+\unicode[STIX]{x1D702}-\unicode[STIX]{x1D701}))\left(r_{\ast }/r_{s}\right)^{2\bar{m}_{-}}$
and
$C_{0}=-(\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D702})\unicode[STIX]{x1D6E4}(-\unicode[STIX]{x1D701})\unicode[STIX]{x1D6E4}(1-\unicode[STIX]{x1D702}+\unicode[STIX]{x1D701}))/(\unicode[STIX]{x1D6E4}(-\unicode[STIX]{x1D702})\unicode[STIX]{x1D6E4}(\unicode[STIX]{x1D701})\unicode[STIX]{x1D6E4}(1+\unicode[STIX]{x1D702}-\unicode[STIX]{x1D701}))\left(r_{\ast }/r_{s}\right)^{2\bar{m}_{-}}$
and
![]() $\ell =\unicode[STIX]{x1D706}+1$
. Thus by means of (3.6) it is straightforward to obtain:
$\ell =\unicode[STIX]{x1D706}+1$
. Thus by means of (3.6) it is straightforward to obtain:
When
![]() $(r_{s}/r_{\ast })^{\unicode[STIX]{x1D706}}\sim 1$
it is possible to show that
$(r_{s}/r_{\ast })^{\unicode[STIX]{x1D706}}\sim 1$
it is possible to show that
![]() $\mathbb{C}_{-}\sim \text{O}(z-1)$
. However since generally speaking the ratio
$\mathbb{C}_{-}\sim \text{O}(z-1)$
. However since generally speaking the ratio
![]() $(r_{s}/r_{\ast })^{\unicode[STIX]{x1D706}}$
is neither small nor close to unity, in the numerical computation of the dispersion relation we shall use the complete expression obtained from (3.5).
$(r_{s}/r_{\ast })^{\unicode[STIX]{x1D706}}$
is neither small nor close to unity, in the numerical computation of the dispersion relation we shall use the complete expression obtained from (3.5).
3.3 Upper sideband (
 $m_{+}=m_{0}+1$
)
$m_{+}=m_{0}+1$
)
It is easy to show that with the safety factor given by (3.1) the resonant surface of the mode
![]() $(m_{0}+1,n)$
occurs at
$(m_{0}+1,n)$
occurs at
![]() $r_{+}=r_{s}[1+2m_{0}[(r_{\ast }/r_{s})^{\unicode[STIX]{x1D706}}-1]/(m_{0}+1)]^{1/\unicode[STIX]{x1D706}}$
. Hence the expression for the upper sideband regular on the axis (
$r_{+}=r_{s}[1+2m_{0}[(r_{\ast }/r_{s})^{\unicode[STIX]{x1D706}}-1]/(m_{0}+1)]^{1/\unicode[STIX]{x1D706}}$
. Hence the expression for the upper sideband regular on the axis (
![]() $X_{+}<\infty$
) reads:
$X_{+}<\infty$
) reads:
where
![]() $\tilde{z}=(r/r_{+})^{\unicode[STIX]{x1D706}}$
,
$\tilde{z}=(r/r_{+})^{\unicode[STIX]{x1D706}}$
,
![]() $\tilde{\unicode[STIX]{x1D702}}=(m_{+}-\bar{m}_{+})/\unicode[STIX]{x1D706}$
,
$\tilde{\unicode[STIX]{x1D702}}=(m_{+}-\bar{m}_{+})/\unicode[STIX]{x1D706}$
,
![]() $\tilde{\unicode[STIX]{x1D701}}=(m_{+}+\bar{m}_{+})/\unicode[STIX]{x1D706}$
,
$\tilde{\unicode[STIX]{x1D701}}=(m_{+}+\bar{m}_{+})/\unicode[STIX]{x1D706}$
,
![]() $\bar{m}_{+}=\sqrt{m_{+}^{2}+2\unicode[STIX]{x1D706}+\unicode[STIX]{x1D706}^{2}}$
. Thus if
$\bar{m}_{+}=\sqrt{m_{+}^{2}+2\unicode[STIX]{x1D706}+\unicode[STIX]{x1D706}^{2}}$
. Thus if
![]() $(r_{\ast }/r_{s})^{\unicode[STIX]{x1D706}}\gg 1$
and
$(r_{\ast }/r_{s})^{\unicode[STIX]{x1D706}}\gg 1$
and
![]() $m_{0}\gg 1$
then
$m_{0}\gg 1$
then
![]() $r_{+}/r_{\ast }\sim 2^{1/\unicode[STIX]{x1D706}}$
so that from (3.8) we obtain:
$r_{+}/r_{\ast }\sim 2^{1/\unicode[STIX]{x1D706}}$
so that from (3.8) we obtain:
Conversely in the limit
![]() $(r_{\ast }/r_{s})^{\unicode[STIX]{x1D706}}\sim 1+\unicode[STIX]{x1D6FF}$
with
$(r_{\ast }/r_{s})^{\unicode[STIX]{x1D706}}\sim 1+\unicode[STIX]{x1D6FF}$
with
![]() $\unicode[STIX]{x1D6FF}\ll 1$
we have
$\unicode[STIX]{x1D6FF}\ll 1$
we have
![]() $(r_{+}/r_{\ast })^{\unicode[STIX]{x1D706}}\sim 1+\unicode[STIX]{x1D6FF}_{\ast }$
with
$(r_{+}/r_{\ast })^{\unicode[STIX]{x1D706}}\sim 1+\unicode[STIX]{x1D6FF}_{\ast }$
with
![]() $\unicode[STIX]{x1D6FF}_{\ast }=(m_{0}-1)/(m_{0}+1)\unicode[STIX]{x1D6FF}$
, which yields:
$\unicode[STIX]{x1D6FF}_{\ast }=(m_{0}-1)/(m_{0}+1)\unicode[STIX]{x1D6FF}$
, which yields:
In order to avoid approximations which could introduce unphysical behaviours, as in the case for the lower sideband, the full expression for
![]() $X_{+}$
(i.e. (3.8)) is preferred when the growth rate is computed numerically.
$X_{+}$
(i.e. (3.8)) is preferred when the growth rate is computed numerically.
In the next sections the quantities
![]() $\mathbb{C}_{\pm }$
will be matched to the low-shear region solutions and then used for the evaluation of the dispersion relation.
$\mathbb{C}_{\pm }$
will be matched to the low-shear region solutions and then used for the evaluation of the dispersion relation.
4 Vacuum region
In the vacuum region the magnetic field must fulfil the conditions
![]() $\unicode[STIX]{x1D735}\times \boldsymbol{B}=\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{B}=0$
. Hence we write
$\unicode[STIX]{x1D735}\times \boldsymbol{B}=\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{B}=0$
. Hence we write
![]() $\boldsymbol{B}=\unicode[STIX]{x1D735}\unicode[STIX]{x1D712}$
with the constraint
$\boldsymbol{B}=\unicode[STIX]{x1D735}\unicode[STIX]{x1D712}$
with the constraint
![]() $\unicode[STIX]{x1D735}^{2}\unicode[STIX]{x1D712}=0$
(Wesson Reference Wesson1978). In large aspect ratio and under the assumption
$\unicode[STIX]{x1D735}^{2}\unicode[STIX]{x1D712}=0$
(Wesson Reference Wesson1978). In large aspect ratio and under the assumption
![]() $m>n$
for each Fourier harmonic, the equation determining the
$m>n$
for each Fourier harmonic, the equation determining the
![]() $m$
th component of the vacuum perturbation reads:
$m$
th component of the vacuum perturbation reads:
Recalling that
![]() $\tilde{B}_{m}^{r}=\unicode[STIX]{x1D712}_{m}^{\prime }$
, this gives
$\tilde{B}_{m}^{r}=\unicode[STIX]{x1D712}_{m}^{\prime }$
, this gives
![]() $\tilde{B}_{m}^{r}\sim (r/b)^{-m-1}-D(r/b)^{m-1}$
for
$\tilde{B}_{m}^{r}\sim (r/b)^{-m-1}-D(r/b)^{m-1}$
for
![]() $a<r<b$
where
$a<r<b$
where
![]() $D$
is a constant determined by the boundary conditions at the plasma–metallic wall interface. In the region
$D$
is a constant determined by the boundary conditions at the plasma–metallic wall interface. In the region
![]() $r>b+d$
the solution of the vacuum perturbation is written in terms of modified Bessel functions (Lashmore-Davies Reference Lashmore-Davies2001). However for
$r>b+d$
the solution of the vacuum perturbation is written in terms of modified Bessel functions (Lashmore-Davies Reference Lashmore-Davies2001). However for
![]() $r\gtrsim b+d$
the behaviour of the radial perturbed magnetic field is well approximated by
$r\gtrsim b+d$
the behaviour of the radial perturbed magnetic field is well approximated by
![]() $\tilde{B}_{m}^{r}\sim (r/b)^{-m-1}$
(Mikhailovskii Reference Mikhailovskii1998; Lashmore-Davies Reference Lashmore-Davies2001).
$\tilde{B}_{m}^{r}\sim (r/b)^{-m-1}$
(Mikhailovskii Reference Mikhailovskii1998; Lashmore-Davies Reference Lashmore-Davies2001).
By means of Faraday’s law
![]() $\boldsymbol{E}=\unicode[STIX]{x1D702}\boldsymbol{J}$
, and assuming that the radial derivatives of the perturbation are dominant, the equation for the perturbation within the wall is:
$\boldsymbol{E}=\unicode[STIX]{x1D702}\boldsymbol{J}$
, and assuming that the radial derivatives of the perturbation are dominant, the equation for the perturbation within the wall is:
In the thin wall approximation (
![]() $d/b\ll 1$
) (Gimblett Reference Gimblett1986) we integrate (4.2) across the wall, so that
$d/b\ll 1$
) (Gimblett Reference Gimblett1986) we integrate (4.2) across the wall, so that
![]() $[r(\tilde{B}_{m}^{r})^{\prime }/\tilde{B}_{m}^{r}]_{b}^{b+d}=(\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D714}_{A})S_{w}(d/b)$
with
$[r(\tilde{B}_{m}^{r})^{\prime }/\tilde{B}_{m}^{r}]_{b}^{b+d}=(\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D714}_{A})S_{w}(d/b)$
with
![]() $S_{w}=\unicode[STIX]{x1D70E}b^{2}\unicode[STIX]{x1D714}_{A}$
. Here
$S_{w}=\unicode[STIX]{x1D70E}b^{2}\unicode[STIX]{x1D714}_{A}$
. Here
![]() $\unicode[STIX]{x1D714}_{A}$
is computed in the plasma core. Requiring continuity of
$\unicode[STIX]{x1D714}_{A}$
is computed in the plasma core. Requiring continuity of
![]() $\tilde{B}_{m}^{r}$
across the thin wall and employing the wall jump condition gives
$\tilde{B}_{m}^{r}$
across the thin wall and employing the wall jump condition gives
![]() $D=F/(F+2m)$
where
$D=F/(F+2m)$
where
![]() $F=(\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D714}_{A})S_{w}(d/b)$
. We stress the point that the constant
$F=(\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D714}_{A})S_{w}(d/b)$
. We stress the point that the constant
![]() $D$
depends on
$D$
depends on
![]() $m$
, thus it varies for different Fourier modes. Note that if we consider the case of a perfectly conducting wall (i.e.
$m$
, thus it varies for different Fourier modes. Note that if we consider the case of a perfectly conducting wall (i.e.
![]() $\unicode[STIX]{x1D702}\rightarrow 0$
,
$\unicode[STIX]{x1D702}\rightarrow 0$
,
![]() $S_{w}\rightarrow \infty$
) we must have
$S_{w}\rightarrow \infty$
) we must have
![]() $D=1$
. Hence
$D=1$
. Hence
![]() $\tilde{B}_{m}^{r}=0$
for any
$\tilde{B}_{m}^{r}=0$
for any
![]() $m$
which corresponds to the condition
$m$
which corresponds to the condition
![]() $\hat{\boldsymbol{n}}\boldsymbol{\cdot }\boldsymbol{B}=0$
where
$\hat{\boldsymbol{n}}\boldsymbol{\cdot }\boldsymbol{B}=0$
where
![]() $\hat{\boldsymbol{n}}$
is the normal vector pointing outward the
$\hat{\boldsymbol{n}}$
is the normal vector pointing outward the
![]() $r=a$
surface (we identify
$r=a$
surface (we identify
![]() $\hat{\boldsymbol{n}}\equiv \unicode[STIX]{x1D735}r$
) (Bernstein et al.
Reference Bernstein, Frieman, Kruskal and Kulsrud1958; Wesson Reference Wesson1978; Freidberg Reference Freidberg1987).
$\hat{\boldsymbol{n}}\equiv \unicode[STIX]{x1D735}r$
) (Bernstein et al.
Reference Bernstein, Frieman, Kruskal and Kulsrud1958; Wesson Reference Wesson1978; Freidberg Reference Freidberg1987).
The jump condition at the plasma–vacuum interface is (Bernstein et al. Reference Bernstein, Frieman, Kruskal and Kulsrud1958; Freidberg Reference Freidberg1987):
where
![]() $\unicode[STIX]{x27E6}\cdot \unicode[STIX]{x27E7}_{a}=(\cdot )_{a+\unicode[STIX]{x1D6FF}}-(\cdot )_{a-\unicode[STIX]{x1D6FF}}$
with
$\unicode[STIX]{x27E6}\cdot \unicode[STIX]{x27E7}_{a}=(\cdot )_{a+\unicode[STIX]{x1D6FF}}-(\cdot )_{a-\unicode[STIX]{x1D6FF}}$
with
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
. By means of (2.6) we can extend the definition of perturbed displacement
$\unicode[STIX]{x1D6FF}\rightarrow 0$
. By means of (2.6) we can extend the definition of perturbed displacement
![]() $X$
outside the plasma, i.e. we write
$X$
outside the plasma, i.e. we write
![]() $\tilde{B}^{r}$
in terms of
$\tilde{B}^{r}$
in terms of
![]() $X$
. This yields
$X$
. This yields
![]() $\tilde{B}_{m}^{r}\sim k_{||,m}X_{m}$
so that since
$\tilde{B}_{m}^{r}\sim k_{||,m}X_{m}$
so that since
![]() $\tilde{B}_{m}^{r}$
must be continuous (cf. (4.3)),
$\tilde{B}_{m}^{r}$
must be continuous (cf. (4.3)),
![]() $X_{m}$
also is continuous since
$X_{m}$
also is continuous since
![]() $k_{||}$
is continuous by hypothesis. It follows that the vacuum perturbation fulfils (2.7). Thus it is easy to see that in the vacuum for a generic Fourier mode
$k_{||}$
is continuous by hypothesis. It follows that the vacuum perturbation fulfils (2.7). Thus it is easy to see that in the vacuum for a generic Fourier mode
![]() $m$
we have (Wesson Reference Wesson1978; Mikhailovskii Reference Mikhailovskii1998):
$m$
we have (Wesson Reference Wesson1978; Mikhailovskii Reference Mikhailovskii1998):
 $$\begin{eqnarray}\displaystyle & \displaystyle \left.{\displaystyle \frac{rX_{m}^{\prime }}{X_{m}}}\right|_{a+\unicode[STIX]{x1D6FF}}={\displaystyle \frac{2\unicode[STIX]{x1D707}_{\ast }}{\unicode[STIX]{x1D707}_{\ast }-n/m}}-{\displaystyle \frac{m+1+\displaystyle {\displaystyle \frac{F}{F+2m}}(m-1)\left(a/b\right)^{2m}}{1-\displaystyle {\displaystyle \frac{F}{F+2m}}\left(a/b\right)^{2m}}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \left.{\displaystyle \frac{rX_{m}^{\prime }}{X_{m}}}\right|_{a+\unicode[STIX]{x1D6FF}}={\displaystyle \frac{2\unicode[STIX]{x1D707}_{\ast }}{\unicode[STIX]{x1D707}_{\ast }-n/m}}-{\displaystyle \frac{m+1+\displaystyle {\displaystyle \frac{F}{F+2m}}(m-1)\left(a/b\right)^{2m}}{1-\displaystyle {\displaystyle \frac{F}{F+2m}}\left(a/b\right)^{2m}}}, & \displaystyle\end{eqnarray}$$
where in the vacuum
![]() $\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{\ast }a^{2}/r^{2}$
(i.e. vanishing toroidal current) (Mikhailovskii Reference Mikhailovskii1998). Let us introduce the notation
$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}_{\ast }a^{2}/r^{2}$
(i.e. vanishing toroidal current) (Mikhailovskii Reference Mikhailovskii1998). Let us introduce the notation
![]() $\mathbb{B}_{\pm }=(rX_{m_{0}\pm 1}^{\prime }/X_{m_{0}\pm 1})|_{a+\unicode[STIX]{x1D6FF}}$
. We point out that, as calculated in § 3, because we approximate
$\mathbb{B}_{\pm }=(rX_{m_{0}\pm 1}^{\prime }/X_{m_{0}\pm 1})|_{a+\unicode[STIX]{x1D6FF}}$
. We point out that, as calculated in § 3, because we approximate
![]() $\unicode[STIX]{x1D707}_{\ast }\approx n/m_{0}$
,
$\unicode[STIX]{x1D707}_{\ast }\approx n/m_{0}$
,
![]() $\unicode[STIX]{x1D6FF}q$
corrections
$\unicode[STIX]{x1D6FF}q$
corrections
![]() $\mathbb{B}_{\pm }$
are not taken into account.
$\mathbb{B}_{\pm }$
are not taken into account.
For the Fourier mode
![]() $m_{0}$
, since
$m_{0}$
, since
![]() $\unicode[STIX]{x1D707}_{\ast }-n/m_{0}\sim \unicode[STIX]{x1D6FF}q\ll 1$
we set
$\unicode[STIX]{x1D707}_{\ast }-n/m_{0}\sim \unicode[STIX]{x1D6FF}q\ll 1$
we set
![]() $X_{m}(a)\approx 0$
. This can be deduced by the fact that close to
$X_{m}(a)\approx 0$
. This can be deduced by the fact that close to
![]() $a$
the eigenfunction behaves as
$a$
the eigenfunction behaves as
![]() $X_{m_{0}}(r)\sim (X_{m_{0}}(a)/\unicode[STIX]{x1D6FF}q)[1-(a/b)^{2m_{0}}D]$
, where obviously
$X_{m_{0}}(r)\sim (X_{m_{0}}(a)/\unicode[STIX]{x1D6FF}q)[1-(a/b)^{2m_{0}}D]$
, where obviously
![]() $D$
is computed for the mode
$D$
is computed for the mode
![]() $m_{0}$
. According to (4.3) the displacement is continuous across
$m_{0}$
. According to (4.3) the displacement is continuous across
![]() $a$
, thus in order to prevent
$a$
, thus in order to prevent
![]() $X_{m_{0}}$
to become arbitrarily large when
$X_{m_{0}}$
to become arbitrarily large when
![]() $\unicode[STIX]{x1D6FF}q\ll 1$
, in general we must set
$\unicode[STIX]{x1D6FF}q\ll 1$
, in general we must set
![]() $X_{m_{0}}(a)=0$
. In the case of an ideal or nearly ideal wall we note that in the vacuum region the equation describing the perturbation is (2.7) (having introduced the quantity
$X_{m_{0}}(a)=0$
. In the case of an ideal or nearly ideal wall we note that in the vacuum region the equation describing the perturbation is (2.7) (having introduced the quantity
![]() $X_{m}$
also in the vacuum). Thus if we multiply (2.7) by
$X_{m}$
also in the vacuum). Thus if we multiply (2.7) by
![]() $X_{m_{0}}$
and integrate by parts from
$X_{m_{0}}$
and integrate by parts from
![]() $a$
to
$a$
to
![]() $b$
we obtain (3.2) with the replacements
$b$
we obtain (3.2) with the replacements
![]() $r_{\ast }\rightarrow a$
and
$r_{\ast }\rightarrow a$
and
![]() $a\rightarrow b$
. Since
$a\rightarrow b$
. Since
![]() $k_{||,m_{0}}^{2}(a)\ll 1$
and
$k_{||,m_{0}}^{2}(a)\ll 1$
and
![]() $X_{m_{0}}(b)=0$
eventually to leading order we get
$X_{m_{0}}(b)=0$
eventually to leading order we get
![]() $X_{m_{0}}=0$
. We shall still approximate
$X_{m_{0}}=0$
. We shall still approximate
![]() $X_{m_{0}}(a)\approx 0$
when the resonance
$X_{m_{0}}(a)\approx 0$
when the resonance
![]() $q=m_{0}/n$
is in the vacuum gap if the resonant point is sufficiently close to
$q=m_{0}/n$
is in the vacuum gap if the resonant point is sufficiently close to
![]() $a$
.
$a$
.
As in the treatment of the sheared region, the logarithmic derivatives of the sideband harmonics are required for matching with the solutions in the low-shear region when the dispersion relation is derived. This will be shown in the next section.
5 Low-shear region matching and dispersion relation
In this section we solve for the main mode and the sideband harmonics deriving eventually the dispersion relation. In this region of width
![]() $a-r_{\ast }=\unicode[STIX]{x1D6E5}\sim \unicode[STIX]{x1D700}\ll 1$
, large pressure gradients drive large edge bootstrap current contributions which in turn flatten the safety factor. There are several choices for the equilibrium profiles for
$a-r_{\ast }=\unicode[STIX]{x1D6E5}\sim \unicode[STIX]{x1D700}\ll 1$
, large pressure gradients drive large edge bootstrap current contributions which in turn flatten the safety factor. There are several choices for the equilibrium profiles for
![]() $p_{0}$
and
$p_{0}$
and
![]() $\unicode[STIX]{x1D70C}_{0}$
(e.g. linear, piecewise continuous polynomials etc.) which allow for an exact treatment of the perturbation. Our analysis concentrates first on a case in which the profiles are step-like and then on a more realistic tanh type profiles. The step-like case has been already treated in Brunetti et al. (Reference Brunetti, Graves, Lazzaro, Mariani, Nowak, Cooper and Wahlberg2018) and it turns out to be useful when toroidal rotation is considered (this is not discussed here). In the next subsection we limit to summarise the findings and to show the mathematical procedure for the derivation of the dispersion relation. Part of these techniques are employed when the tanh model is considered, though a slightly different approach must be used.
$\unicode[STIX]{x1D70C}_{0}$
(e.g. linear, piecewise continuous polynomials etc.) which allow for an exact treatment of the perturbation. Our analysis concentrates first on a case in which the profiles are step-like and then on a more realistic tanh type profiles. The step-like case has been already treated in Brunetti et al. (Reference Brunetti, Graves, Lazzaro, Mariani, Nowak, Cooper and Wahlberg2018) and it turns out to be useful when toroidal rotation is considered (this is not discussed here). In the next subsection we limit to summarise the findings and to show the mathematical procedure for the derivation of the dispersion relation. Part of these techniques are employed when the tanh model is considered, though a slightly different approach must be used.
5.1 Step-like functions
In order to mimic the abrupt decrease of the pressure and mass density in the flat-
![]() $q$
region (Burrell et al.
Reference Burrell, Austin, Brennan, DeBoo, Doyle, Fenzi, Fuchs, Gohil, Greenfield and Groebner2001, Reference Burrell, West, Doyle, Austin, Casper, Gohil, Greenfield, Groebner, Hyatt and Jayakumar2005), following Wahlberg et al. (Reference Wahlberg, Graves and Chapman2013) we introduce step-like profiles:
$q$
region (Burrell et al.
Reference Burrell, Austin, Brennan, DeBoo, Doyle, Fenzi, Fuchs, Gohil, Greenfield and Groebner2001, Reference Burrell, West, Doyle, Austin, Casper, Gohil, Greenfield, Groebner, Hyatt and Jayakumar2005), following Wahlberg et al. (Reference Wahlberg, Graves and Chapman2013) we introduce step-like profiles:
where
![]() $\unicode[STIX]{x1D6E9}(x)$
is the Heaviside step function of argument
$\unicode[STIX]{x1D6E9}(x)$
is the Heaviside step function of argument
![]() $x$
,
$x$
,
![]() $r_{p}=(a+r_{\ast })/2$
and
$r_{p}=(a+r_{\ast })/2$
and
![]() $p_{\ast }$
is the value of plasma pressure at
$p_{\ast }$
is the value of plasma pressure at
![]() $r_{\ast }$
. The mass density is assumed constant in
$r_{\ast }$
. The mass density is assumed constant in
![]() $0<r<r_{\ast }$
.
$0<r<r_{\ast }$
.
By integrating once (2.9) we obtain:
Integration of (2.9) across
![]() $r_{p}$
gives
$r_{p}$
gives
![]() $\unicode[STIX]{x27E6}(r^{2\pm m_{0}}X_{\pm })^{\prime }\unicode[STIX]{x27E7}_{r_{p}}=0$
implying that in (5.2) we must have
$\unicode[STIX]{x27E6}(r^{2\pm m_{0}}X_{\pm })^{\prime }\unicode[STIX]{x27E7}_{r_{p}}=0$
implying that in (5.2) we must have
![]() $L_{\pm }(r<r_{p})=L_{\pm }(r>r_{p})$
, i.e. the constant
$L_{\pm }(r<r_{p})=L_{\pm }(r>r_{p})$
, i.e. the constant
![]() $L_{+}$
(or
$L_{+}$
(or
![]() $L_{-}$
) on the left and on the right of
$L_{-}$
) on the left and on the right of
![]() $r_{p}$
must be the same. Thus plugging (5.2) into (2.8), under the assumption
$r_{p}$
must be the same. Thus plugging (5.2) into (2.8), under the assumption
![]() $(1/q^{2}-1)\approx -1$
, yields:
$(1/q^{2}-1)\approx -1$
, yields:
where
![]() $\hat{\unicode[STIX]{x1D6FE}}^{2}=\unicode[STIX]{x1D6FE}^{2}(1+2q^{2})/(n\unicode[STIX]{x1D714}_{A})^{2}$
.
$\hat{\unicode[STIX]{x1D6FE}}^{2}=\unicode[STIX]{x1D6FE}^{2}(1+2q^{2})/(n\unicode[STIX]{x1D714}_{A})^{2}$
.
The three harmonics must be supplied with appropriate boundary conditions. The solution of the main harmonic
![]() $m_{0}$
in the sheared and vacuum regions (cf. §§ 3.1 and 4) provides the constraint:
$m_{0}$
in the sheared and vacuum regions (cf. §§ 3.1 and 4) provides the constraint:
The boundary conditions for the sideband harmonics are obtained by integrating (2.9) across
![]() $r_{\ast }$
and
$r_{\ast }$
and
![]() $a$
. Since the pressure and its gradient at these points are vanishingly small, this yields:
$a$
. Since the pressure and its gradient at these points are vanishingly small, this yields:
where the quantities
![]() $\mathbb{C}_{\pm }$
and
$\mathbb{C}_{\pm }$
and
![]() $\mathbb{B}_{\pm }$
have been evaluated in §§ 3 and 4 respectively.
$\mathbb{B}_{\pm }$
have been evaluated in §§ 3 and 4 respectively.
Before solving for the main harmonic we first determine the constants
![]() $L_{\pm }$
. These are obtained by evaluating (5.2) at
$L_{\pm }$
. These are obtained by evaluating (5.2) at
![]() $r_{\ast }$
and
$r_{\ast }$
and
![]() $a$
and using the constraint (5.4). Since the pressure gradient and
$a$
and using the constraint (5.4). Since the pressure gradient and
![]() $X_{m_{0}}$
are vanishing at the plasma boundary, we obtain
$X_{m_{0}}$
are vanishing at the plasma boundary, we obtain
![]() $X_{\pm }(r_{\ast })=r_{\ast }^{\pm m_{0}}L_{\pm }/(2\pm m_{0}+\mathbb{C}_{\pm })$
and
$X_{\pm }(r_{\ast })=r_{\ast }^{\pm m_{0}}L_{\pm }/(2\pm m_{0}+\mathbb{C}_{\pm })$
and
![]() $X_{\pm }(a)=a^{\pm m_{0}}L_{\pm }/(2\pm m_{0}+\mathbb{B}_{\pm })$
. By means of (5.1), integration of (5.2) from
$X_{\pm }(a)=a^{\pm m_{0}}L_{\pm }/(2\pm m_{0}+\mathbb{B}_{\pm })$
. By means of (5.1), integration of (5.2) from
![]() $r_{\ast }$
to
$r_{\ast }$
to
![]() $a$
finally gives
$a$
finally gives
![]() $(r_{p}^{\pm m_{0}}L_{\pm }/1\pm m_{0})=X_{0}(\hat{\unicode[STIX]{x1D6FD}}/\unicode[STIX]{x1D700}_{p})\unicode[STIX]{x1D6EC}^{(\pm )}$
where
$(r_{p}^{\pm m_{0}}L_{\pm }/1\pm m_{0})=X_{0}(\hat{\unicode[STIX]{x1D6FD}}/\unicode[STIX]{x1D700}_{p})\unicode[STIX]{x1D6EC}^{(\pm )}$
where
![]() $\hat{\unicode[STIX]{x1D6FD}}=2p_{\ast }q^{2}/B_{0}^{2}$
,
$\hat{\unicode[STIX]{x1D6FD}}=2p_{\ast }q^{2}/B_{0}^{2}$
,
![]() $\unicode[STIX]{x1D700}_{p}=r_{p}/R_{0}$
and (Gimblett et al.
Reference Gimblett, Hastie and Hender1996):
$\unicode[STIX]{x1D700}_{p}=r_{p}/R_{0}$
and (Gimblett et al.
Reference Gimblett, Hastie and Hender1996):
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6EC}^{(\pm )}={\displaystyle \frac{(r_{p}/r_{\ast })^{2\pm 2m_{0}}(1\pm m_{0})[2\pm m_{0}+\mathbb{C}_{\pm }][2\pm m_{0}+\mathbb{B}_{\pm }]}{(\mathbb{C}_{\pm }\mp m_{0})[2\pm m_{0}+\mathbb{B}_{\pm }]-(\mathbb{B}_{\pm }\mp m_{0})[2\pm m_{0}+\mathbb{C}_{\pm }]\left({\displaystyle \frac{a}{r_{\ast }}}\right)^{2\pm 2m_{0}}}}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6EC}^{(\pm )}={\displaystyle \frac{(r_{p}/r_{\ast })^{2\pm 2m_{0}}(1\pm m_{0})[2\pm m_{0}+\mathbb{C}_{\pm }][2\pm m_{0}+\mathbb{B}_{\pm }]}{(\mathbb{C}_{\pm }\mp m_{0})[2\pm m_{0}+\mathbb{B}_{\pm }]-(\mathbb{B}_{\pm }\mp m_{0})[2\pm m_{0}+\mathbb{C}_{\pm }]\left({\displaystyle \frac{a}{r_{\ast }}}\right)^{2\pm 2m_{0}}}}. & \displaystyle\end{eqnarray}$$
Integration of (5.2) and (5.3) across
![]() $r_{p}$
with the profiles given in (5.1), shows that the singularities arising from
$r_{p}$
with the profiles given in (5.1), shows that the singularities arising from
![]() $p_{0}^{\prime }$
and
$p_{0}^{\prime }$
and
![]() $\unicode[STIX]{x1D70C}_{0}^{\prime }$
produce discontinuities at this point of
$\unicode[STIX]{x1D70C}_{0}^{\prime }$
produce discontinuities at this point of
![]() $X_{\pm }$
,
$X_{\pm }$
,
![]() $X_{\pm }^{\prime }$
and
$X_{\pm }^{\prime }$
and
![]() $X_{m_{0}}^{\prime }$
while
$X_{m_{0}}^{\prime }$
while
![]() $X_{m_{0}}$
remains continuous. By means of (5.1), the equation for
$X_{m_{0}}$
remains continuous. By means of (5.1), the equation for
![]() $X_{m_{0}}$
is greatly simplified:
$X_{m_{0}}$
is greatly simplified:
The equation above is solved separately for
![]() $r<r_{p}$
and
$r<r_{p}$
and
![]() $r>r_{p}$
imposing continuity at
$r>r_{p}$
imposing continuity at
![]() $r_{p}$
and the constraints (5.4), giving:
$r_{p}$
and the constraints (5.4), giving:
 $$\begin{eqnarray}\displaystyle X_{m_{0}}=X_{0}\times \left\{\begin{array}{@{}ll@{}}\displaystyle {\displaystyle \frac{\left({\displaystyle \frac{r}{r_{\ast }}}\right)^{m_{0}-1}-\left({\displaystyle \frac{r}{r_{\ast }}}\right)^{-m_{0}-1}}{\left({\displaystyle \frac{r_{p}}{r_{\ast }}}\right)^{m_{0}-1}-\left({\displaystyle \frac{r_{p}}{r_{\ast }}}\right)^{-m_{0}-1}}}, & r<r_{p},\\[31.20007pt] \displaystyle {\displaystyle \frac{\left({\displaystyle \frac{r}{a}}\right)^{m_{0}-1}-\left({\displaystyle \frac{r}{a}}\right)^{-m_{0}-1}}{\left({\displaystyle \frac{r_{p}}{a}}\right)^{m_{0}-1}-\left({\displaystyle \frac{r_{p}}{a}}\right)^{-m_{0}-1}}}, & r>r_{p}.\end{array}\right. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X_{m_{0}}=X_{0}\times \left\{\begin{array}{@{}ll@{}}\displaystyle {\displaystyle \frac{\left({\displaystyle \frac{r}{r_{\ast }}}\right)^{m_{0}-1}-\left({\displaystyle \frac{r}{r_{\ast }}}\right)^{-m_{0}-1}}{\left({\displaystyle \frac{r_{p}}{r_{\ast }}}\right)^{m_{0}-1}-\left({\displaystyle \frac{r_{p}}{r_{\ast }}}\right)^{-m_{0}-1}}}, & r<r_{p},\\[31.20007pt] \displaystyle {\displaystyle \frac{\left({\displaystyle \frac{r}{a}}\right)^{m_{0}-1}-\left({\displaystyle \frac{r}{a}}\right)^{-m_{0}-1}}{\left({\displaystyle \frac{r_{p}}{a}}\right)^{m_{0}-1}-\left({\displaystyle \frac{r_{p}}{a}}\right)^{-m_{0}-1}}}, & r>r_{p}.\end{array}\right. & & \displaystyle\end{eqnarray}$$
Following Wahlberg et al. (Reference Wahlberg, Graves and Chapman2013), the dispersion relation is obtained by integrating (5.3) across
![]() $r_{p}$
. This gives:
$r_{p}$
. This gives:
Let us introduce
![]() $g_{\pm }=(rX_{m_{0}}^{\prime }/X_{m_{0}})|_{r_{p}^{\pm }}$
. By means of (5.8), it is easy to show that if
$g_{\pm }=(rX_{m_{0}}^{\prime }/X_{m_{0}})|_{r_{p}^{\pm }}$
. By means of (5.8), it is easy to show that if
![]() $r_{p}\approx a$
and
$r_{p}\approx a$
and
![]() $m_{0}\sim 1$
then
$m_{0}\sim 1$
then
![]() $g_{-}\approx -g_{+}\approx 2a/\unicode[STIX]{x1D6E5}$
. Hence (5.9) becomes:
$g_{-}\approx -g_{+}\approx 2a/\unicode[STIX]{x1D6E5}$
. Hence (5.9) becomes:
The last term on the right-hand side of (5.10) corresponds to the Mercier term in (2.8) and has a weak stabilising influence. It is clear that the instability drive are the pressure gradient and the field line bending weakening. This dispersion relation has been discussed in detail in Brunetti et al. (Reference Brunetti, Graves, Lazzaro, Mariani, Nowak, Cooper and Wahlberg2018). We shall now use this result as a reference for the more realistic tanh case presented in the next section.
5.2 Tanh model
In this section we model
![]() $p_{0}$
and
$p_{0}$
and
![]() $\unicode[STIX]{x1D70C}_{0}$
with more realistic smooth profiles. It is important to note that since the step and the corresponding discontinuities at
$\unicode[STIX]{x1D70C}_{0}$
with more realistic smooth profiles. It is important to note that since the step and the corresponding discontinuities at
![]() $r_{p}$
are lost, in order to derive the dispersion relation we must adopt a different procedure compared to the one employed in the previous case.
$r_{p}$
are lost, in order to derive the dispersion relation we must adopt a different procedure compared to the one employed in the previous case.
The total pressure is written as
![]() $p_{0}=n_{0}(T_{i}+T_{e})$
where
$p_{0}=n_{0}(T_{i}+T_{e})$
where
![]() $T_{s}$
is the temperature of the
$T_{s}$
is the temperature of the
![]() $s$
species and
$s$
species and
![]() $n_{0}$
the numerical density (quasineutrality is imposed). Assuming that the electron temperature profile is proportional to the density profile, i.e.
$n_{0}$
the numerical density (quasineutrality is imposed). Assuming that the electron temperature profile is proportional to the density profile, i.e.
![]() $T_{e}\approx T_{e0}n_{0}/\bar{n}$
(
$T_{e}\approx T_{e0}n_{0}/\bar{n}$
(
![]() $\bar{n}$
is the value of the numerical density in the core), and
$\bar{n}$
is the value of the numerical density in the core), and
![]() $T_{i}\gg T_{e0}$
with
$T_{i}\gg T_{e0}$
with
![]() $T_{i}^{\prime }\sim 0$
we eventually obtain
$T_{i}^{\prime }\sim 0$
we eventually obtain
![]() $p_{0}\sim n_{0}T_{i}$
and
$p_{0}\sim n_{0}T_{i}$
and
![]() $p_{0}^{\prime }\sim n_{0}^{\prime }T_{i}$
. Hence pressure and mass density have approximately the same shape (Zheng et al.
Reference Zheng, Kotschenreuther and Valanju2013a
,Reference Zheng, Kotschenreuther and Valanju
b
) in qualitative accordance with experimental data (Burrell et al.
Reference Burrell, Austin, Brennan, DeBoo, Doyle, Fenzi, Fuchs, Gohil, Greenfield and Groebner2001, Reference Burrell, West, Doyle, Austin, Casper, Gohil, Greenfield, Groebner, Hyatt and Jayakumar2005). Thus a more realistic choice for the profiles of
$p_{0}^{\prime }\sim n_{0}^{\prime }T_{i}$
. Hence pressure and mass density have approximately the same shape (Zheng et al.
Reference Zheng, Kotschenreuther and Valanju2013a
,Reference Zheng, Kotschenreuther and Valanju
b
) in qualitative accordance with experimental data (Burrell et al.
Reference Burrell, Austin, Brennan, DeBoo, Doyle, Fenzi, Fuchs, Gohil, Greenfield and Groebner2001, Reference Burrell, West, Doyle, Austin, Casper, Gohil, Greenfield, Groebner, Hyatt and Jayakumar2005). Thus a more realistic choice for the profiles of
![]() $p_{0}$
and
$p_{0}$
and
![]() $\unicode[STIX]{x1D70C}_{0}$
is the following:
$\unicode[STIX]{x1D70C}_{0}$
is the following:
where
![]() $\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D6E5}\lesssim 1$
and
$\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D6E5}\lesssim 1$
and
![]() $r_{p}$
has been already defined in the previous section (we recall that
$r_{p}$
has been already defined in the previous section (we recall that
![]() $\unicode[STIX]{x1D6E5}$
is the width of the low-shear region). Note that for
$\unicode[STIX]{x1D6E5}$
is the width of the low-shear region). Note that for
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
we shall recover the step-like case (this will be indeed shown later).
$\unicode[STIX]{x1D6FF}\rightarrow 0$
we shall recover the step-like case (this will be indeed shown later).
In this region we adopt the ordering presented in (2.15), and therefore we employ (2.16) and (2.17). As in the previous section, we integrate once (2.17) and we plug the result into (2.16) obtaining:
where explicitly
![]() $Q=Z[1-c\tanh x/\unicode[STIX]{x1D6FF}]$
with
$Q=Z[1-c\tanh x/\unicode[STIX]{x1D6FF}]$
with
![]() $Z=(\unicode[STIX]{x1D6FF}q/q)^{2}+\hat{\unicode[STIX]{x1D6FE}}^{2}/2$
and
$Z=(\unicode[STIX]{x1D6FF}q/q)^{2}+\hat{\unicode[STIX]{x1D6FE}}^{2}/2$
and
![]() $c=\hat{\unicode[STIX]{x1D6FE}}^{2}/2Z$
. The solution of (5.12) is easily obtained and it reads:
$c=\hat{\unicode[STIX]{x1D6FE}}^{2}/2Z$
. The solution of (5.12) is easily obtained and it reads:
where
![]() $x=r-r_{p}$
and
$x=r-r_{p}$
and
![]() $H=(q^{2}p_{\ast }/2)/(B_{0}^{2}Z\unicode[STIX]{x1D700})[(\hat{L}_{+}/a)/(1+m_{0})+(\hat{L}_{-}/a)/(1-m_{0})]$
.
$H=(q^{2}p_{\ast }/2)/(B_{0}^{2}Z\unicode[STIX]{x1D700})[(\hat{L}_{+}/a)/(1+m_{0})+(\hat{L}_{-}/a)/(1-m_{0})]$
.
The constants
![]() $c_{1,2}$
of the main harmonic are determined by imposing the boundary conditions (5.4) yielding (
$c_{1,2}$
of the main harmonic are determined by imposing the boundary conditions (5.4) yielding (
![]() $h=\unicode[STIX]{x1D6E5}/2$
):
$h=\unicode[STIX]{x1D6E5}/2$
):
By integrating (2.17) across
![]() $a$
and
$a$
and
![]() $r_{\ast }$
under the assumption that the pressure gradient is not too large at these points, employing (5.4) we find that the sidebands fulfil (5.5).
$r_{\ast }$
under the assumption that the pressure gradient is not too large at these points, employing (5.4) we find that the sidebands fulfil (5.5).
As shown in the previous section, to compute the constants
![]() $\hat{L}_{\pm }$
equation (5.13) is first evaluated both at
$\hat{L}_{\pm }$
equation (5.13) is first evaluated both at
![]() $r_{\ast }$
and
$r_{\ast }$
and
![]() $a$
and then integrated from
$a$
and then integrated from
![]() $r_{\ast }$
to
$r_{\ast }$
to
![]() $a$
yielding:
$a$
yielding:
We immediately note that
![]() $\hat{L}_{\pm }(X_{m_{0}})$
are linear in
$\hat{L}_{\pm }(X_{m_{0}})$
are linear in
![]() $X_{m_{0}}$
, i.e. for
$X_{m_{0}}$
, i.e. for
![]() $k$
constant
$k$
constant
![]() $k\hat{L}_{\pm }(X_{m_{0}})=\hat{L}_{\pm }(kX_{m_{0}})$
. The expressions for
$k\hat{L}_{\pm }(X_{m_{0}})=\hat{L}_{\pm }(kX_{m_{0}})$
. The expressions for
![]() $\hat{L}_{\pm }$
are inserted into the equation for the main harmonic (5.12) and the result is divided by the real number
$\hat{L}_{\pm }$
are inserted into the equation for the main harmonic (5.12) and the result is divided by the real number
![]() $\int _{r_{\ast }}^{a}\unicode[STIX]{x1D6FC}X_{m_{0}}\,\text{d}r$
. The solution to this equation is still given by (5.14) with an appropriate rescaling of the constants
$\int _{r_{\ast }}^{a}\unicode[STIX]{x1D6FC}X_{m_{0}}\,\text{d}r$
. The solution to this equation is still given by (5.14) with an appropriate rescaling of the constants
![]() $c_{1,2}$
(i.e. the term
$c_{1,2}$
(i.e. the term
![]() $H$
). Hence this is equivalent to solve (5.12) imposing the integral condition (Wahlberg & Graves Reference Wahlberg and Graves2007):
$H$
). Hence this is equivalent to solve (5.12) imposing the integral condition (Wahlberg & Graves Reference Wahlberg and Graves2007):
Equation (5.17) provides the dispersion relation with
![]() $\hat{L}_{\pm }=(\mathbb{B}_{\pm }\mathbb{C}_{\pm }(1\pm m_{0})/(2a))/$
$\hat{L}_{\pm }=(\mathbb{B}_{\pm }\mathbb{C}_{\pm }(1\pm m_{0})/(2a))/$
![]() $[\mathbb{C}_{\pm }-\mathbb{B}_{\pm }-\mathbb{B}_{\pm }\mathbb{C}_{\pm }\unicode[STIX]{x1D6E5}/a]$
. Plugging (5.14) and (5.15) into (5.17), some straightforward algebra produces the following result:
$[\mathbb{C}_{\pm }-\mathbb{B}_{\pm }-\mathbb{B}_{\pm }\mathbb{C}_{\pm }\unicode[STIX]{x1D6E5}/a]$
. Plugging (5.14) and (5.15) into (5.17), some straightforward algebra produces the following result:
where
![]() $\hat{\unicode[STIX]{x1D6FD}}$
has been introduced in the previous section and
$\hat{\unicode[STIX]{x1D6FD}}$
has been introduced in the previous section and
![]() $A_{\unicode[STIX]{x1D6FE}}=h/c$
$A_{\unicode[STIX]{x1D6FE}}=h/c$
![]() $[(ch/\unicode[STIX]{x1D6FF}-\tanh ^{-1}(c\tanh (h/\unicode[STIX]{x1D6FF})))/(h/\unicode[STIX]{x1D6FF}-c\tanh ^{-1}(c\tanh (h/\unicode[STIX]{x1D6FF})))]$
. We shall now analyse more in detail the dispersion relation equation (5.18) and the associated eigenfunctions.
$[(ch/\unicode[STIX]{x1D6FF}-\tanh ^{-1}(c\tanh (h/\unicode[STIX]{x1D6FF})))/(h/\unicode[STIX]{x1D6FF}-c\tanh ^{-1}(c\tanh (h/\unicode[STIX]{x1D6FF})))]$
. We shall now analyse more in detail the dispersion relation equation (5.18) and the associated eigenfunctions.
6 Analysis of the dispersion relation of the tanh model
The main difficulty arising in the solution of (5.18) is the dependence upon the growth rate embedded in the function
![]() $A_{\unicode[STIX]{x1D6FE}}$
, i.e. inside the coefficient
$A_{\unicode[STIX]{x1D6FE}}$
, i.e. inside the coefficient
![]() $c$
. Generally speaking the solution of such a dispersion relation must be tackled numerically. Nonetheless an explicit dependence of
$c$
. Generally speaking the solution of such a dispersion relation must be tackled numerically. Nonetheless an explicit dependence of
![]() $\unicode[STIX]{x1D6FE}$
on the plasma parameters can be obtained for some special cases.
$\unicode[STIX]{x1D6FE}$
on the plasma parameters can be obtained for some special cases.
Let us consider first the case of a perfectly conducting wall (
![]() $\unicode[STIX]{x1D70E}\rightarrow \infty$
). If the metallic wall is directly interfaced with the plasma then
$\unicode[STIX]{x1D70E}\rightarrow \infty$
). If the metallic wall is directly interfaced with the plasma then
![]() $\mathbb{B}_{\pm }\rightarrow \infty$
and because
$\mathbb{B}_{\pm }\rightarrow \infty$
and because
![]() $\mathbb{C}_{\pm }>0$
we immediately have
$\mathbb{C}_{\pm }>0$
we immediately have
![]() $\hat{L}_{\pm }\lessgtr 0$
. Therefore, since
$\hat{L}_{\pm }\lessgtr 0$
. Therefore, since
![]() $A_{\unicode[STIX]{x1D6FE}}>0$
, the right-hand side of (5.18) is negative indicating stability. Thus with ideal wall boundary conditions, a vacuum region is necessary for the instability to develop. This also suggests a threshold in the wall position for the growth rate in accordance with the results presented in Zheng et al. (Reference Zheng, Kotschenreuther and Valanju2013a
,Reference Zheng, Kotschenreuther and Valanju
b
).
$A_{\unicode[STIX]{x1D6FE}}>0$
, the right-hand side of (5.18) is negative indicating stability. Thus with ideal wall boundary conditions, a vacuum region is necessary for the instability to develop. This also suggests a threshold in the wall position for the growth rate in accordance with the results presented in Zheng et al. (Reference Zheng, Kotschenreuther and Valanju2013a
,Reference Zheng, Kotschenreuther and Valanju
b
).
Let us now examine the behaviour of
![]() $A_{\unicode[STIX]{x1D6FE}}$
near marginal stability (
$A_{\unicode[STIX]{x1D6FE}}$
near marginal stability (
![]() $c\ll 1$
) and in the strong instability region (
$c\ll 1$
) and in the strong instability region (
![]() $c\sim 1$
). By taking the corresponding limits we obtain at leading order:
$c\sim 1$
). By taking the corresponding limits we obtain at leading order:
Thus the
![]() $\unicode[STIX]{x1D6FE}$
dependence in
$\unicode[STIX]{x1D6FE}$
dependence in
![]() $A_{\unicode[STIX]{x1D6FE}}$
is removed and an explicit expression for the growth rate can be obtained. The resulting growth rates with respect to the plasma parameters are shown in figure 2.
$A_{\unicode[STIX]{x1D6FE}}$
is removed and an explicit expression for the growth rate can be obtained. The resulting growth rates with respect to the plasma parameters are shown in figure 2.
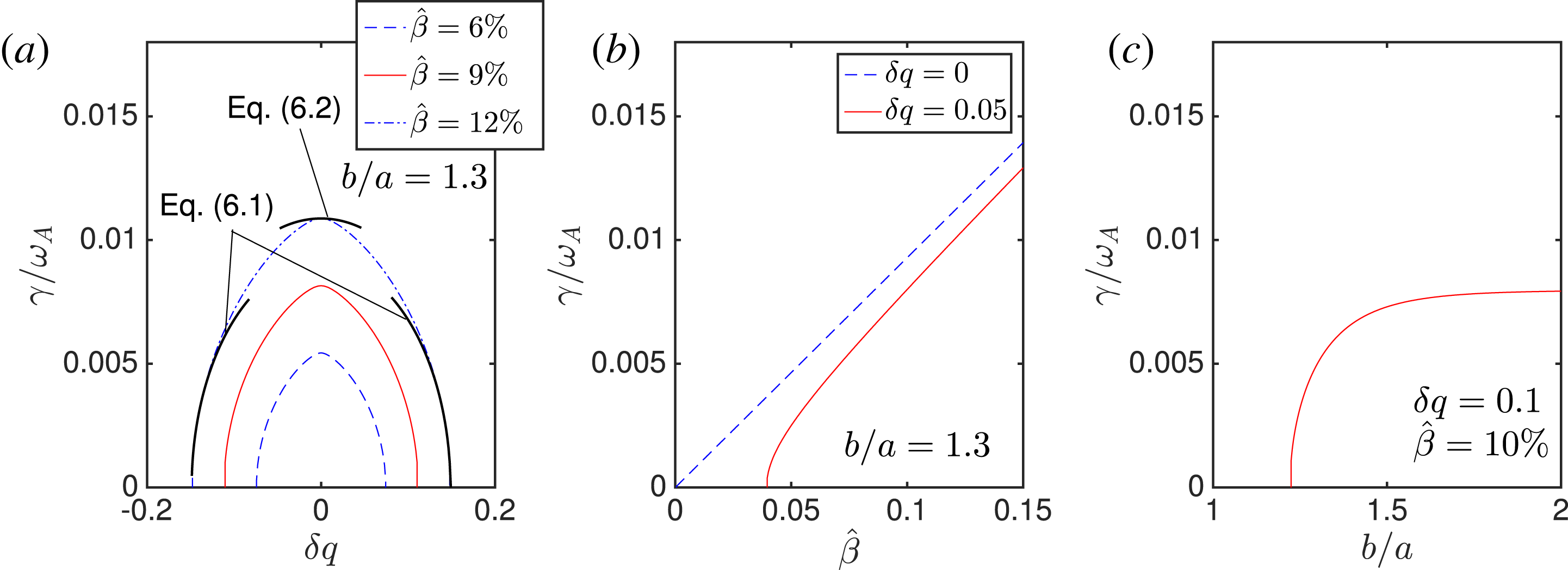
Figure 2. Ideal wall boundary condition growth rates for the main mode
![]() $m_{0}/n=4/1$
with
$m_{0}/n=4/1$
with
![]() $q(r_{\ast })=m_{0}/n-\unicode[STIX]{x1D6FF}q$
,
$q(r_{\ast })=m_{0}/n-\unicode[STIX]{x1D6FF}q$
,
![]() $\unicode[STIX]{x1D700}=1/3$
,
$\unicode[STIX]{x1D700}=1/3$
,
![]() $r_{s}=0.8$
,
$r_{s}=0.8$
,
![]() $\unicode[STIX]{x1D706}=2$
,
$\unicode[STIX]{x1D706}=2$
,
![]() $r_{\ast }/a=0.95$
and
$r_{\ast }/a=0.95$
and
![]() $h/\unicode[STIX]{x1D6FF}=3$
with respect to
$h/\unicode[STIX]{x1D6FF}=3$
with respect to
![]() $\unicode[STIX]{x1D6FF}q$
(a),
$\unicode[STIX]{x1D6FF}q$
(a),
![]() $\hat{\unicode[STIX]{x1D6FD}}$
(b) and wall position (c). Note that
$\hat{\unicode[STIX]{x1D6FD}}$
(b) and wall position (c). Note that
![]() $\hat{\unicode[STIX]{x1D6FD}}$
can be moderately large due to the factor
$\hat{\unicode[STIX]{x1D6FD}}$
can be moderately large due to the factor
![]() $q^{2}$
. The asymptotic behaviour obtained from formulae (6.1) and (6.2) is shown in (a).
$q^{2}$
. The asymptotic behaviour obtained from formulae (6.1) and (6.2) is shown in (a).
It is worth noticing that particular attention has to be devoted to the expansion of
![]() $A_{\unicode[STIX]{x1D6FE}}$
near
$A_{\unicode[STIX]{x1D6FE}}$
near
![]() $c=1$
. Indeed a series expansion
$c=1$
. Indeed a series expansion
![]() $A_{\unicode[STIX]{x1D6FE}}$
in
$A_{\unicode[STIX]{x1D6FE}}$
in
![]() $(c-1)$
cannot be performed if
$(c-1)$
cannot be performed if
![]() $h/\unicode[STIX]{x1D6FF}$
becomes sufficiently large. Therefore we decided to retain only the first term which provides the correct asymptotic behaviour for
$h/\unicode[STIX]{x1D6FF}$
becomes sufficiently large. Therefore we decided to retain only the first term which provides the correct asymptotic behaviour for
![]() $h/\unicode[STIX]{x1D6FF}\rightarrow \infty$
. In such a case (
$h/\unicode[STIX]{x1D6FF}\rightarrow \infty$
. In such a case (
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
) it is easy to see that both for
$\unicode[STIX]{x1D6FF}\rightarrow 0$
) it is easy to see that both for
![]() $c\ll 1$
and
$c\ll 1$
and
![]() $c\sim 1$
the step-like dispersion relation (cf. (5.10)) is formally recovered substituting
$c\sim 1$
the step-like dispersion relation (cf. (5.10)) is formally recovered substituting
![]() $\unicode[STIX]{x1D6EC}^{(\pm )}\rightarrow \hat{L}_{\pm }$
and without the Mercier contribution (this has been dropped due to the ordering (2.15)). The shape of the eigenfunctions also qualitatively reduces to the step-like case as shown in figure 3. Differences remain due to the fact that in the system of equations (5.12) and (5.13) we dropped terms which conversely are retained in (5.2) and (5.3). In addition we point out that in the tanh model, contrarily to the step case, the shape of the eigenfunctions depends on the value of
$\unicode[STIX]{x1D6EC}^{(\pm )}\rightarrow \hat{L}_{\pm }$
and without the Mercier contribution (this has been dropped due to the ordering (2.15)). The shape of the eigenfunctions also qualitatively reduces to the step-like case as shown in figure 3. Differences remain due to the fact that in the system of equations (5.12) and (5.13) we dropped terms which conversely are retained in (5.2) and (5.3). In addition we point out that in the tanh model, contrarily to the step case, the shape of the eigenfunctions depends on the value of
![]() $\unicode[STIX]{x1D6FF}q$
(and so on the corresponding growth rate). We note that the radial structure of the main and sidebands harmonics closely resembles what has been found numerically in three-dimensional equilibria simulations (Cooper et al.
Reference Cooper, Graves, Duval, Porte, Reimerdes, Sauter and Tran2015, Reference Cooper, Brunetti, Duval, Faustin, Graves, Kleiner, Patten, Pfefferlé, Porte and Raghunathan2016a
,Reference Cooper, Graves, Duval, Sauter, Faustin, Kleiner, Lanthaler, Patten, Raghunathan and Tran
b
) and in MHD stability calculations (Medvedev et al.
Reference Medvedev, Martynov, Martin, Sauter and Villard2006; Zheng et al.
Reference Zheng, Kotschenreuther and Valanju2013a
,Reference Zheng, Kotschenreuther and Valanju
b
).
$\unicode[STIX]{x1D6FF}q$
(and so on the corresponding growth rate). We note that the radial structure of the main and sidebands harmonics closely resembles what has been found numerically in three-dimensional equilibria simulations (Cooper et al.
Reference Cooper, Graves, Duval, Porte, Reimerdes, Sauter and Tran2015, Reference Cooper, Brunetti, Duval, Faustin, Graves, Kleiner, Patten, Pfefferlé, Porte and Raghunathan2016a
,Reference Cooper, Graves, Duval, Sauter, Faustin, Kleiner, Lanthaler, Patten, Raghunathan and Tran
b
) and in MHD stability calculations (Medvedev et al.
Reference Medvedev, Martynov, Martin, Sauter and Villard2006; Zheng et al.
Reference Zheng, Kotschenreuther and Valanju2013a
,Reference Zheng, Kotschenreuther and Valanju
b
).

Figure 3. Plot of the eigenfunctions normalised with respect to the maximum of the main mode
![]() $m_{0}=4,n=1$
(
$m_{0}=4,n=1$
(
![]() $X_{M}$
) for the tanh (a)–(b) and the step-like model (c) with an ideal wall boundary condition with
$X_{M}$
) for the tanh (a)–(b) and the step-like model (c) with an ideal wall boundary condition with
![]() $\unicode[STIX]{x1D700}=1/3$
,
$\unicode[STIX]{x1D700}=1/3$
,
![]() $\hat{\unicode[STIX]{x1D6FD}}=3\,\%$
,
$\hat{\unicode[STIX]{x1D6FD}}=3\,\%$
,
![]() $r_{s}=0.8$
,
$r_{s}=0.8$
,
![]() $\unicode[STIX]{x1D706}=2$
,
$\unicode[STIX]{x1D706}=2$
,
![]() $r_{\ast }/a=0.95$
and
$r_{\ast }/a=0.95$
and
![]() $q_{\ast }\approx 4$
. In (a) and (b) the eigenfunctions are computed for
$q_{\ast }\approx 4$
. In (a) and (b) the eigenfunctions are computed for
![]() $\unicode[STIX]{x1D6FF}q=0.03$
corresponding to
$\unicode[STIX]{x1D6FF}q=0.03$
corresponding to
![]() $\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D714}_{A}\approx 1.4\times 10^{-3}$
. The dashed vertical line indicates the position of the low-shear region middle point
$\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D714}_{A}\approx 1.4\times 10^{-3}$
. The dashed vertical line indicates the position of the low-shear region middle point
![]() $r_{p}$
. We set in (a)
$r_{p}$
. We set in (a)
![]() $h/\unicode[STIX]{x1D6FF}=3$
while in (b)
$h/\unicode[STIX]{x1D6FF}=3$
while in (b)
![]() $h/\unicode[STIX]{x1D6FF}=20$
. Qualitatively the behaviour of the step model is recovered for large
$h/\unicode[STIX]{x1D6FF}=20$
. Qualitatively the behaviour of the step model is recovered for large
![]() $h/\unicode[STIX]{x1D6FF}$
. Note that the maximum of the main harmonic (
$h/\unicode[STIX]{x1D6FF}$
. Note that the maximum of the main harmonic (
![]() $m_{0}=4$
) in the tanh model is slightly shifted to the right with respect to
$m_{0}=4$
) in the tanh model is slightly shifted to the right with respect to
![]() $r_{p}$
.
$r_{p}$
.
We shall now consider the case with a resistive wall. For sake of simplicity in the following analysis we set
![]() $\unicode[STIX]{x1D714}_{A}=1$
. We assume that the conductivity is sufficiently large so that we can expand
$\unicode[STIX]{x1D714}_{A}=1$
. We assume that the conductivity is sufficiently large so that we can expand
![]() $\mathbb{B}_{\pm }$
in
$\mathbb{B}_{\pm }$
in
![]() $1/\unicode[STIX]{x1D70E}$
. This yields
$1/\unicode[STIX]{x1D70E}$
. This yields
![]() $\mathbb{B}_{\pm }=\mathbb{B}_{\pm }|_{\unicode[STIX]{x1D70E}=\infty }+(\mathbb{B}_{\pm }^{w}/(S_{w}\unicode[STIX]{x1D6FE}(d/b)))$
with:
$\mathbb{B}_{\pm }=\mathbb{B}_{\pm }|_{\unicode[STIX]{x1D70E}=\infty }+(\mathbb{B}_{\pm }^{w}/(S_{w}\unicode[STIX]{x1D6FE}(d/b)))$
with:
Inserting (6.3) into the expressions for
![]() $\hat{L}_{\pm }$
, to leading order we obtain:
$\hat{L}_{\pm }$
, to leading order we obtain:
where
![]() $\mathbb{B}_{\pm }^{0}=\mathbb{B}_{\pm }|_{\unicode[STIX]{x1D70E}=\infty }$
. Let us formally write the expression above as
$\mathbb{B}_{\pm }^{0}=\mathbb{B}_{\pm }|_{\unicode[STIX]{x1D70E}=\infty }$
. Let us formally write the expression above as
![]() $(\hat{L}_{\pm }/1\pm m_{0})\approx \mathscr{D}_{\pm }+\mathscr{R}_{\pm }/(S_{w}\unicode[STIX]{x1D6FE})$
. Hence the equation (5.18) can be cast in the following manner:
$(\hat{L}_{\pm }/1\pm m_{0})\approx \mathscr{D}_{\pm }+\mathscr{R}_{\pm }/(S_{w}\unicode[STIX]{x1D6FE})$
. Hence the equation (5.18) can be cast in the following manner:
where
![]() $\hat{\unicode[STIX]{x1D6FE}}_{I}^{2}=2(\hat{\unicode[STIX]{x1D6FD}}/2\unicode[STIX]{x1D700})^{2}h[\mathscr{D}_{+}+\mathscr{D}_{-}]$
is the growth rate with the ideal wall and:
$\hat{\unicode[STIX]{x1D6FE}}_{I}^{2}=2(\hat{\unicode[STIX]{x1D6FD}}/2\unicode[STIX]{x1D700})^{2}h[\mathscr{D}_{+}+\mathscr{D}_{-}]$
is the growth rate with the ideal wall and:
having assumed for sake of simplicity that
![]() $h/\unicode[STIX]{x1D6FF}\gg 1$
, i.e.
$h/\unicode[STIX]{x1D6FF}\gg 1$
, i.e.
![]() $A_{\unicode[STIX]{x1D6FE}}\rightarrow h$
.
$A_{\unicode[STIX]{x1D6FE}}\rightarrow h$
.
Suppose that
![]() $\hat{\unicode[STIX]{x1D6FE}}_{I}^{2}>0$
. Therefore if
$\hat{\unicode[STIX]{x1D6FE}}_{I}^{2}>0$
. Therefore if
![]() $\unicode[STIX]{x1D6FE}_{w}/\hat{\unicode[STIX]{x1D6FE}}_{I}\ll 1$
, the growth rate can be written as
$\unicode[STIX]{x1D6FE}_{w}/\hat{\unicode[STIX]{x1D6FE}}_{I}\ll 1$
, the growth rate can be written as
![]() $\hat{\unicode[STIX]{x1D6FE}}=\hat{\unicode[STIX]{x1D6FE}}_{I}+(\unicode[STIX]{x1D6FE}_{w}^{3}/2\hat{\unicode[STIX]{x1D6FE}}_{I}^{2})$
. Conversely if
$\hat{\unicode[STIX]{x1D6FE}}=\hat{\unicode[STIX]{x1D6FE}}_{I}+(\unicode[STIX]{x1D6FE}_{w}^{3}/2\hat{\unicode[STIX]{x1D6FE}}_{I}^{2})$
. Conversely if
![]() $\unicode[STIX]{x1D6FE}_{w}/\hat{\unicode[STIX]{x1D6FE}}_{I}\gg 1$
, the growth rate is
$\unicode[STIX]{x1D6FE}_{w}/\hat{\unicode[STIX]{x1D6FE}}_{I}\gg 1$
, the growth rate is
![]() $\hat{\unicode[STIX]{x1D6FE}}=\unicode[STIX]{x1D6FE}_{w}+(\hat{\unicode[STIX]{x1D6FE}}_{I}^{2}/3\unicode[STIX]{x1D6FE}_{w})$
. In both cases the destabilising effect of the resistive wall is evident. In the opposite case, when
$\hat{\unicode[STIX]{x1D6FE}}=\unicode[STIX]{x1D6FE}_{w}+(\hat{\unicode[STIX]{x1D6FE}}_{I}^{2}/3\unicode[STIX]{x1D6FE}_{w})$
. In both cases the destabilising effect of the resistive wall is evident. In the opposite case, when
![]() $\hat{\unicode[STIX]{x1D6FE}}_{I}^{2}<0$
and
$\hat{\unicode[STIX]{x1D6FE}}_{I}^{2}<0$
and
![]() $\unicode[STIX]{x1D6FE}_{w}$
are sufficiently small (i.e. we are in the stability region with the ideal wall) instability is still possible with growth rate
$\unicode[STIX]{x1D6FE}_{w}$
are sufficiently small (i.e. we are in the stability region with the ideal wall) instability is still possible with growth rate
![]() $\hat{\unicode[STIX]{x1D6FE}}=\unicode[STIX]{x1D6FE}_{w}^{3}/|\hat{\unicode[STIX]{x1D6FE}}_{I}^{2}|$
. The behaviour of
$\hat{\unicode[STIX]{x1D6FE}}=\unicode[STIX]{x1D6FE}_{w}^{3}/|\hat{\unicode[STIX]{x1D6FE}}_{I}^{2}|$
. The behaviour of
![]() $\unicode[STIX]{x1D6FE}_{w}$
with respect to
$\unicode[STIX]{x1D6FE}_{w}$
with respect to
![]() $n$
is shown in figure 4.
$n$
is shown in figure 4.
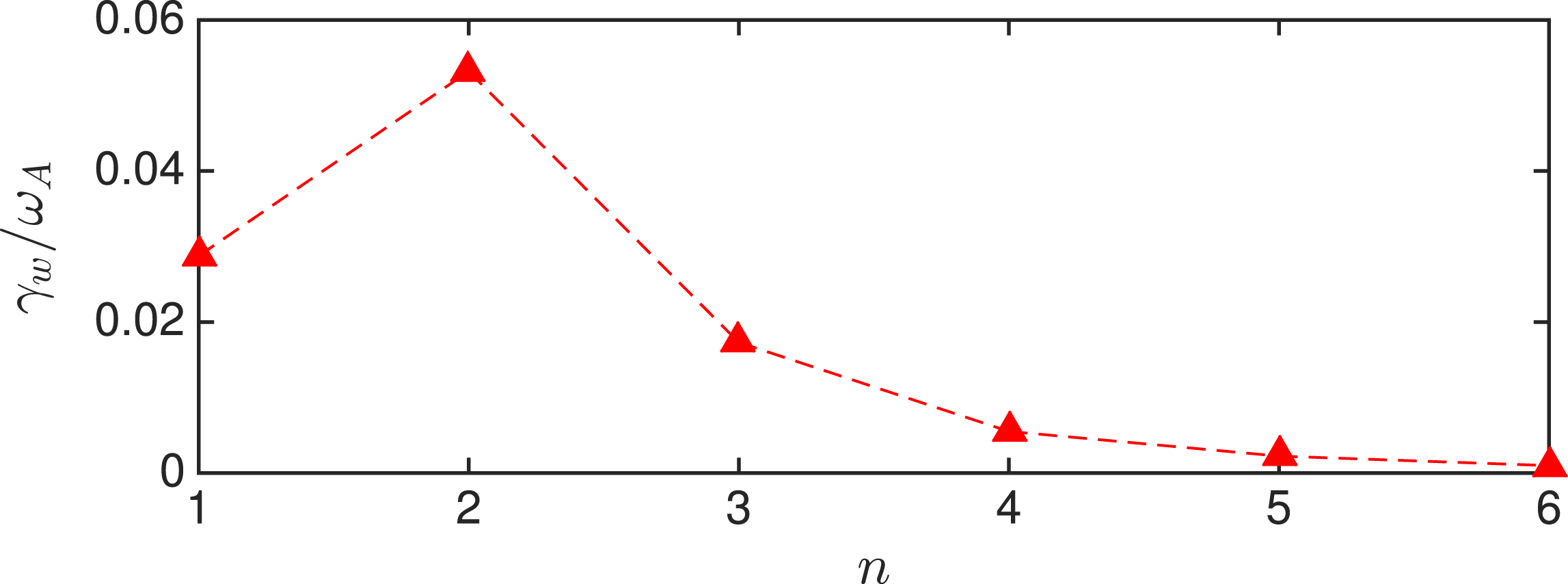
Figure 4. Plot of
![]() $\unicode[STIX]{x1D6FE}_{w}/\unicode[STIX]{x1D714}_{A}$
with respect to the toroidal mode number
$\unicode[STIX]{x1D6FE}_{w}/\unicode[STIX]{x1D714}_{A}$
with respect to the toroidal mode number
![]() $n$
with
$n$
with
![]() $\unicode[STIX]{x1D700}=1/3$
,
$\unicode[STIX]{x1D700}=1/3$
,
![]() $b/a=1.3$
,
$b/a=1.3$
,
![]() $d/a=10^{-2}$
$d/a=10^{-2}$
![]() $\hat{\unicode[STIX]{x1D6FD}}=5\,\%$
,
$\hat{\unicode[STIX]{x1D6FD}}=5\,\%$
,
![]() $r_{s}=0.8$
,
$r_{s}=0.8$
,
![]() $\unicode[STIX]{x1D706}=2$
,
$\unicode[STIX]{x1D706}=2$
,
![]() $r_{\ast }/a=0.95$
,
$r_{\ast }/a=0.95$
,
![]() $S_{w}=10^{5}$
and
$S_{w}=10^{5}$
and
![]() $q_{\ast }=4$
(here we have dropped the normalisation
$q_{\ast }=4$
(here we have dropped the normalisation
![]() $\unicode[STIX]{x1D714}_{A}=1$
). Note that
$\unicode[STIX]{x1D714}_{A}=1$
). Note that
![]() $\unicode[STIX]{x1D6FE}_{w}/\unicode[STIX]{x1D714}_{A}$
peaks for small values of
$\unicode[STIX]{x1D6FE}_{w}/\unicode[STIX]{x1D714}_{A}$
peaks for small values of
![]() $n$
.
$n$
.
Although toroidal rotation effects are not considered in the present work, based on the results shown in Brunetti et al. (Reference Brunetti, Graves, Lazzaro, Mariani, Nowak, Cooper and Wahlberg2018) we expect that the rotation induced Doppler shift should be included in the low-shear inertial contribution with a modification of the dispersion relation (
![]() $\unicode[STIX]{x1D6FA}$
is the rotation frequency evaluated at
$\unicode[STIX]{x1D6FA}$
is the rotation frequency evaluated at
![]() $r_{\ast }$
):
$r_{\ast }$
):
It is easy to see that for sufficiently large toroidal rotation, the resistive wall effects become negligible.
7 Conclusions
In this work we addressed the linear stability properties of infernal type perturbations with a safety factor flat and close to a rational number (
![]() $q\approx m_{0}/n$
) near the edge. This perturbation presents a main (
$q\approx m_{0}/n$
) near the edge. This perturbation presents a main (
![]() $m_{0},n$
) Fourier harmonic, resonant in the flat
$m_{0},n$
) Fourier harmonic, resonant in the flat
![]() $q$
region, which is coupled with its neighbouring sidebands (
$q$
region, which is coupled with its neighbouring sidebands (
![]() $m_{0}\pm 1,n$
). Although it is well known that plasma resistivity can grow to large values near the edge (Turnbull et al.
Reference Turnbull, Hanson, Turco, Ferraro, Lanctot, Lao, Strait, Piovesan and Martin2016), the standard ideal MHD model has been adopted. This is motivated by the fact that the
$m_{0}\pm 1,n$
). Although it is well known that plasma resistivity can grow to large values near the edge (Turnbull et al.
Reference Turnbull, Hanson, Turco, Ferraro, Lanctot, Lao, Strait, Piovesan and Martin2016), the standard ideal MHD model has been adopted. This is motivated by the fact that the
![]() $m$
values resonating with the edge
$m$
values resonating with the edge
![]() $q$
must be moderately large, and thus they are expected to be stable against standard tearing perturbations (Hegna & Callen Reference Hegna and Callen1994).
$q$
must be moderately large, and thus they are expected to be stable against standard tearing perturbations (Hegna & Callen Reference Hegna and Callen1994).
An exact analytic treatment of the magnetic perturbation in the inner region of large magnetic shear has been possible with a careful choice, although rather general, of the safety factor. In the region of the local edge flattening of the safety factor, the equilibrium profiles for pressure and mass density have been modelled with two simple classes of analytic functions. In one case (already discussed in Brunetti et al. (Reference Brunetti, Graves, Lazzaro, Mariani, Nowak, Cooper and Wahlberg2018)) the step-like model has been employed. In the second case we introduced a layer ordering in the low-shear region resulting in a simplification of the coupled equations. This allowed us to employ a more realistic tanh model. A vacuum region with a parabolic safety factor (
![]() $q\sim r^{2}$
) has been included with either ideally conducting or resistive wall boundary conditions (note that in the ideally conducting wall case, the presence of a vacuum region separating plasma and wall is necessary for the instability to develop). Each region has been analysed separately and the solutions eventually matched across the transitions points. The advantage of this choice for the equilibrium profiles, i.e. safety factor and either step or tanh-like pressure and mass density, consists in an exact mathematical description of both the eigenfunctions and the associated dispersion relation. We point out that additional corrections such as inertia and residual coupling associated with the behaviour of the sidebands inside the sheared region have been neglected (a brief description of their effects is given in the appendices). The dispersion relation which has been derived is sufficiently simple to show the explicit dependence of the growth rate upon the engineering plasma parameters, i.e. plasma current profile and
$q\sim r^{2}$
) has been included with either ideally conducting or resistive wall boundary conditions (note that in the ideally conducting wall case, the presence of a vacuum region separating plasma and wall is necessary for the instability to develop). Each region has been analysed separately and the solutions eventually matched across the transitions points. The advantage of this choice for the equilibrium profiles, i.e. safety factor and either step or tanh-like pressure and mass density, consists in an exact mathematical description of both the eigenfunctions and the associated dispersion relation. We point out that additional corrections such as inertia and residual coupling associated with the behaviour of the sidebands inside the sheared region have been neglected (a brief description of their effects is given in the appendices). The dispersion relation which has been derived is sufficiently simple to show the explicit dependence of the growth rate upon the engineering plasma parameters, i.e. plasma current profile and
![]() $\unicode[STIX]{x1D6FD}$
.
$\unicode[STIX]{x1D6FD}$
.
Similarly to the peeling–ballooning (PB) modes, the drive of the instability is the combined effect of pressure gradients and the edge current (field line bending weakening) which translates in a toroidal coupling of neighbouring poloidal Fourier harmonics. The structure of edge infernal modes resembles the one of PB perturbations (Snyder et al.
Reference Snyder, Wilson, Ferron, Lao, Leonard, Mossessian, Murakami, Osborne, Turnbull and Xu2004), consisting of a non-vanishing peeling component accompanied by an inner located bell-shaped displacement. Hence we can regard these perturbations as very low-
![]() $n$
PB modes. Such a model seems to be appropriate for the description of the edge harmonic oscillations. Indeed the shape of the eigenfunctions calculated analytically exhibits similarities with both numerical results (Medvedev et al.
Reference Medvedev, Martynov, Martin, Sauter and Villard2006; Zheng et al.
Reference Zheng, Kotschenreuther and Valanju2013a
,Reference Zheng, Kotschenreuther and Valanju
b
) and with experimental findings (Chen et al.
Reference Chen, Burrell, Ferraro, Osborne, Austin, Garofalo, Groebner, Kramer, Luhmann and McKee2016) (in particular the bell shape and the radial localisation are correctly recovered by the model we proposed). We also note that experimental measurement of density and temperature fluctuations show even parity (in the radial direction) (Burrell et al.
Reference Burrell, Austin, Brennan, DeBoo, Doyle, Fenzi, Fuchs, Gohil, Greenfield and Groebner2001; Greenfield et al.
Reference Greenfield, Burrell, DeBoo, Doyle, Stallard, Synakowski, Fenzi, Gohil, Groebner and Lao2001), excluding the tearing character of the perturbation and thus supporting even more the ideal plasma approximation.
$n$
PB modes. Such a model seems to be appropriate for the description of the edge harmonic oscillations. Indeed the shape of the eigenfunctions calculated analytically exhibits similarities with both numerical results (Medvedev et al.
Reference Medvedev, Martynov, Martin, Sauter and Villard2006; Zheng et al.
Reference Zheng, Kotschenreuther and Valanju2013a
,Reference Zheng, Kotschenreuther and Valanju
b
) and with experimental findings (Chen et al.
Reference Chen, Burrell, Ferraro, Osborne, Austin, Garofalo, Groebner, Kramer, Luhmann and McKee2016) (in particular the bell shape and the radial localisation are correctly recovered by the model we proposed). We also note that experimental measurement of density and temperature fluctuations show even parity (in the radial direction) (Burrell et al.
Reference Burrell, Austin, Brennan, DeBoo, Doyle, Fenzi, Fuchs, Gohil, Greenfield and Groebner2001; Greenfield et al.
Reference Greenfield, Burrell, DeBoo, Doyle, Stallard, Synakowski, Fenzi, Gohil, Groebner and Lao2001), excluding the tearing character of the perturbation and thus supporting even more the ideal plasma approximation.
It is worth emphasising the facts that this work is based on very simple ‘model’ profiles and is developed in the linear framework. Nevertheless, although the observed perturbations are in their nonlinear stage, we shall expect that the linear structural properties (shape, parity, location of (main) peak) may persist from the linear into the nonlinear stage.
It is found that in the case of ideal wall boundary conditions the growth rates become larger with increasing
![]() $n$
(Zheng et al.
Reference Zheng, Kotschenreuther and Valanju2013b
; Liu et al.
Reference Liu, Huijsmans, Loarte, Garofalo, Solomon, Snyder, Hoelzl and Zeng2015). This might be relevant for QH regimes with zero injected torque (Burrell et al.
Reference Burrell, Barada, Chen, Garofalo, Groebner, Muscatello, Osborne, Petty, Rhodes and Snyder2016; Chen et al.
Reference Chen, Burrell, Osborne, Solomon, Barada, Garofalo, Groebner, Luhmann, McKee and Muscatello2017). In such a case a weakly quasi-coherent MHD (broadband) activity with a cessation of the EHO is observed. This could be linked with the nonlinear interplay of different
$n$
(Zheng et al.
Reference Zheng, Kotschenreuther and Valanju2013b
; Liu et al.
Reference Liu, Huijsmans, Loarte, Garofalo, Solomon, Snyder, Hoelzl and Zeng2015). This might be relevant for QH regimes with zero injected torque (Burrell et al.
Reference Burrell, Barada, Chen, Garofalo, Groebner, Muscatello, Osborne, Petty, Rhodes and Snyder2016; Chen et al.
Reference Chen, Burrell, Osborne, Solomon, Barada, Garofalo, Groebner, Luhmann, McKee and Muscatello2017). In such a case a weakly quasi-coherent MHD (broadband) activity with a cessation of the EHO is observed. This could be linked with the nonlinear interplay of different
![]() $n$
values (also moderately large) which are all allowed to grow in the linear phase (Liu et al.
Reference Liu, Huijsmans, Loarte, Garofalo, Solomon, Snyder, Hoelzl and Zeng2015, Reference Liu, Huijsmans, Loarte, Garofalo, Solomon, Hoelzl, Nkonga, Pamela, Becoulet and Orain2018). Consequently in the nonlinear stage they can compete with each other without favouring a particular
$n$
values (also moderately large) which are all allowed to grow in the linear phase (Liu et al.
Reference Liu, Huijsmans, Loarte, Garofalo, Solomon, Snyder, Hoelzl and Zeng2015, Reference Liu, Huijsmans, Loarte, Garofalo, Solomon, Hoelzl, Nkonga, Pamela, Becoulet and Orain2018). Consequently in the nonlinear stage they can compete with each other without favouring a particular
![]() $n$
to be dominant (Liu et al.
Reference Liu, Huijsmans, Loarte, Garofalo, Solomon, Hoelzl, Nkonga, Pamela, Becoulet and Orain2018). The inclusion of a finite wall conductivity has a destabilising effect and near the ideal wall marginal stability boundary the resistive wall growth rate peaks for small values of the toroidal (poloidal) mode numbers.
$n$
to be dominant (Liu et al.
Reference Liu, Huijsmans, Loarte, Garofalo, Solomon, Hoelzl, Nkonga, Pamela, Becoulet and Orain2018). The inclusion of a finite wall conductivity has a destabilising effect and near the ideal wall marginal stability boundary the resistive wall growth rate peaks for small values of the toroidal (poloidal) mode numbers.
We point out that from the results obtained in Brunetti et al. (Reference Brunetti, Graves, Lazzaro, Mariani, Nowak, Cooper and Wahlberg2018) with step-like profiles and an ideal wall, a subsonic toroidal rotation Doppler shifts the eigenfrequency. Although in the present work effects of plasma rotation have been neglected, we may argue that also with the tanh model a purely toroidal rotation should enter through a Doppler shift of the eigenfrequencies. This predicts a rotating mode with frequency
![]() $n\unicode[STIX]{x1D6FA}_{\ast }$
(
$n\unicode[STIX]{x1D6FA}_{\ast }$
(
![]() $\unicode[STIX]{x1D6FA}_{\ast }$
is the toroidal rotation at the pedestal top) in accordance with experimental data (see e.g. Burrell et al.
Reference Burrell, Austin, Brennan, DeBoo, Doyle, Fenzi, Fuchs, Gohil, Greenfield and Groebner2001; Greenfield et al.
Reference Greenfield, Burrell, DeBoo, Doyle, Stallard, Synakowski, Fenzi, Gohil, Groebner and Lao2001; Solano et al.
Reference Solano, Lomas, Alper, Xu, Andrew, Arnoux, Boboc, Barrera, Belo and Beurskens2010). We may also expect resistive wall effects to become negligible for sufficiently large toroidal flows (Nave & Wesson Reference Nave and Wesson1990).
$\unicode[STIX]{x1D6FA}_{\ast }$
is the toroidal rotation at the pedestal top) in accordance with experimental data (see e.g. Burrell et al.
Reference Burrell, Austin, Brennan, DeBoo, Doyle, Fenzi, Fuchs, Gohil, Greenfield and Groebner2001; Greenfield et al.
Reference Greenfield, Burrell, DeBoo, Doyle, Stallard, Synakowski, Fenzi, Gohil, Groebner and Lao2001; Solano et al.
Reference Solano, Lomas, Alper, Xu, Andrew, Arnoux, Boboc, Barrera, Belo and Beurskens2010). We may also expect resistive wall effects to become negligible for sufficiently large toroidal flows (Nave & Wesson Reference Nave and Wesson1990).
In addition, as shown in Brunetti et al. (Reference Brunetti, Graves, Lazzaro, Mariani, Nowak, Cooper and Wahlberg2018) in the ideal wall case, the mode stability properties are not altered by a subsonic toroidal flow. Therefore we shall infer that the toroidal rotation alone is not sufficient to explain why in the experiments only a single
![]() $n$
dominant mode is observed (see e.g. (Chen et al.
Reference Chen, Burrell, Ferraro, Osborne, Austin, Garofalo, Groebner, Kramer, Luhmann and McKee2016)). Moreover experimental findings presented in Garofalo et al. (Reference Garofalo, Solomon, Park, Burrell, DeBoo, Lanctot, McKee, Reimerdes, Schmitz and Schaffer2011), Burrell et al. (Reference Burrell, Garofalo, Solomon, Fenstermacher, Osborne, Park, Schaffer and Snyder2012) show that the key ingredient for accessing the QH mode is the shear associated with the
$n$
dominant mode is observed (see e.g. (Chen et al.
Reference Chen, Burrell, Ferraro, Osborne, Austin, Garofalo, Groebner, Kramer, Luhmann and McKee2016)). Moreover experimental findings presented in Garofalo et al. (Reference Garofalo, Solomon, Park, Burrell, DeBoo, Lanctot, McKee, Reimerdes, Schmitz and Schaffer2011), Burrell et al. (Reference Burrell, Garofalo, Solomon, Fenstermacher, Osborne, Park, Schaffer and Snyder2012) show that the key ingredient for accessing the QH mode is the shear associated with the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
drift. This induces us to conclude that diamagnetic drifts and sheared poloidal flows with the associated electric field effects should play a fundamental role in the accessibility of the QH operational space. This thus will require further analytic investigations.
$\boldsymbol{E}\times \boldsymbol{B}$
drift. This induces us to conclude that diamagnetic drifts and sheared poloidal flows with the associated electric field effects should play a fundamental role in the accessibility of the QH operational space. This thus will require further analytic investigations.
Finally we argue that the effects of the separatrix may alter the jump conditions of the magnetic perturbation, resulting in a modification of the dispersion relation. Shaping effects also (mainly elongation) could alter the mode dynamics. It is envisaged that a numerical approach is required to address such a difficult problem.
Appendix A. Effects of inertial corrections on the lower sideband
The quantity
![]() $B_{2}/A_{2}$
which appears in (3.5), depends on the growth rate
$B_{2}/A_{2}$
which appears in (3.5), depends on the growth rate
![]() $\unicode[STIX]{x1D6FE}$
as inertial corrections may become important when the resonant surface of the lower sideband is approached. We expand (3.4) and (3.5) about
$\unicode[STIX]{x1D6FE}$
as inertial corrections may become important when the resonant surface of the lower sideband is approached. We expand (3.4) and (3.5) about
![]() $r_{s}$
giving (we use the same notation as in Mikhailovskii (Reference Mikhailovskii1998), Brunetti, Lazzaro & Nowak (Reference Brunetti, Lazzaro and Nowak2017)):
$r_{s}$
giving (we use the same notation as in Mikhailovskii (Reference Mikhailovskii1998), Brunetti, Lazzaro & Nowak (Reference Brunetti, Lazzaro and Nowak2017)):
where
![]() $\unicode[STIX]{x1D6E5}_{c}=[\unicode[STIX]{x1D702}\unicode[STIX]{x1D701}(2\unicode[STIX]{x1D6FE}_{E}-1+\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D701}+1)+\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D702}+1))-m_{-}-1/\unicode[STIX]{x1D706}]$
(
$\unicode[STIX]{x1D6E5}_{c}=[\unicode[STIX]{x1D702}\unicode[STIX]{x1D701}(2\unicode[STIX]{x1D6FE}_{E}-1+\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D701}+1)+\unicode[STIX]{x1D6F9}(\unicode[STIX]{x1D702}+1))-m_{-}-1/\unicode[STIX]{x1D706}]$
(
![]() $\unicode[STIX]{x1D6FE}_{E}$
is the Euler–Mascheroni constant and
$\unicode[STIX]{x1D6FE}_{E}$
is the Euler–Mascheroni constant and
![]() $\unicode[STIX]{x1D6F9}$
the digamma function (see Abramowitz & Stegun Reference Abramowitz and Stegun1968, p. 253)),
$\unicode[STIX]{x1D6F9}$
the digamma function (see Abramowitz & Stegun Reference Abramowitz and Stegun1968, p. 253)),
![]() $\unicode[STIX]{x1D6E5}_{p}=d_{+}+((B_{{>}}/A_{{>}})/(1+B_{{>}}/A_{{>}}))(d_{-}-d_{+})$
and:
$\unicode[STIX]{x1D6E5}_{p}=d_{+}+((B_{{>}}/A_{{>}})/(1+B_{{>}}/A_{{>}}))(d_{-}-d_{+})$
and:
Equations (A 1) contain a logarithmic term which is generally neglected when the inertial layer is studied in slab geometry. Following the analysis presented in Mikhailovskii (Reference Mikhailovskii1998), we allow for inertial effects in (2.7) close to
![]() $r_{s}$
so that (
$r_{s}$
so that (
![]() $^{\prime }\equiv \text{d}/\text{d}x$
):
$^{\prime }\equiv \text{d}/\text{d}x$
):
where
![]() $z=1+x$
and
$z=1+x$
and
![]() $\bar{\unicode[STIX]{x1D6FE}}^{2}=\unicode[STIX]{x1D6FE}^{2}/(S\unicode[STIX]{x1D714}_{A})^{2}(1+2q^{2})$
. Let us introduce the following ordering:
$\bar{\unicode[STIX]{x1D6FE}}^{2}=\unicode[STIX]{x1D6FE}^{2}/(S\unicode[STIX]{x1D714}_{A})^{2}(1+2q^{2})$
. Let us introduce the following ordering:
![]() $x\sim \bar{\unicode[STIX]{x1D6FE}}\sim \unicode[STIX]{x1D6FF},\text{d}/\text{d}x\sim 1/\unicode[STIX]{x1D6FF}$
with
$x\sim \bar{\unicode[STIX]{x1D6FE}}\sim \unicode[STIX]{x1D6FF},\text{d}/\text{d}x\sim 1/\unicode[STIX]{x1D6FF}$
with
![]() $\unicode[STIX]{x1D6FF}\ll 1$
and
$\unicode[STIX]{x1D6FF}\ll 1$
and
![]() $(m_{-}^{2}-1/\unicode[STIX]{x1D706}^{2})\sim S\sim 1$
. We write the solution as
$(m_{-}^{2}-1/\unicode[STIX]{x1D706}^{2})\sim S\sim 1$
. We write the solution as
![]() $X=X_{0}+\unicode[STIX]{x1D6FF}X_{1}+\text{O}(\unicode[STIX]{x1D6FF}^{2})$
and then expand the equation above in a series of
$X=X_{0}+\unicode[STIX]{x1D6FF}X_{1}+\text{O}(\unicode[STIX]{x1D6FF}^{2})$
and then expand the equation above in a series of
![]() $\unicode[STIX]{x1D6FF}$
. Eventually we have:
$\unicode[STIX]{x1D6FF}$
. Eventually we have:
where
![]() $\pm$
is for
$\pm$
is for
![]() $x\lessgtr 0$
. As
$x\lessgtr 0$
. As
![]() $x/\bar{\unicode[STIX]{x1D6FE}}\rightarrow \infty$
the logarithmic terms in (A 4) are immediately matched with (A 1) by choosing
$x/\bar{\unicode[STIX]{x1D6FE}}\rightarrow \infty$
the logarithmic terms in (A 4) are immediately matched with (A 1) by choosing
![]() $c_{3}=\unicode[STIX]{x1D702}\unicode[STIX]{x1D701}/2$
, while the non-logarithmic part of (A 4) behaves as:
$c_{3}=\unicode[STIX]{x1D702}\unicode[STIX]{x1D701}/2$
, while the non-logarithmic part of (A 4) behaves as:
where
![]() $\pm$
is for
$\pm$
is for
![]() $x\lessgtr 0$
as before. Matching (A 5) with (A 1) gives
$x\lessgtr 0$
as before. Matching (A 5) with (A 1) gives
![]() $\unicode[STIX]{x03C0}/\hat{\unicode[STIX]{x1D6FE}}+\unicode[STIX]{x1D6E5}_{c}+\unicode[STIX]{x1D6E5}_{p}=0$
and eventually we obtain:
$\unicode[STIX]{x03C0}/\hat{\unicode[STIX]{x1D6FE}}+\unicode[STIX]{x1D6E5}_{c}+\unicode[STIX]{x1D6E5}_{p}=0$
and eventually we obtain:
where the last approximation holds if
![]() $\hat{\unicode[STIX]{x1D6FE}}\ll 1$
. For sufficiently small growth rates we have
$\hat{\unicode[STIX]{x1D6FE}}\ll 1$
. For sufficiently small growth rates we have
![]() $B_{{>}}/A_{{>}}=-1$
.
$B_{{>}}/A_{{>}}=-1$
.
Appendix B. Allowance for residual coupling effects at the resonant layer of the lower sideband
We assume that a small coupling contribution remains near the resonant point
![]() $r_{s}$
of the lower harmonic
$r_{s}$
of the lower harmonic
![]() $X_{-}$
. This corresponds to the fact that the main harmonic
$X_{-}$
. This corresponds to the fact that the main harmonic
![]() $m_{0}$
and pressure gradients can be non-exactly vanishing for
$m_{0}$
and pressure gradients can be non-exactly vanishing for
![]() $r<r_{\ast }$
. For sake of simplicity we write
$r<r_{\ast }$
. For sake of simplicity we write
![]() $m=m_{0}-1$
. Thus we modify the (2.7) by adding the constant
$m=m_{0}-1$
. Thus we modify the (2.7) by adding the constant
![]() $U$
which represents the coupling corrections similar to the ones appearing in (2.8) and (2.9):
$U$
which represents the coupling corrections similar to the ones appearing in (2.8) and (2.9):
where here
![]() $Q=k_{||}^{2}+\unicode[STIX]{x1D6FE}^{2}(1+2q^{2})\unicode[STIX]{x1D714}_{A}^{2}$
. We assume that
$Q=k_{||}^{2}+\unicode[STIX]{x1D6FE}^{2}(1+2q^{2})\unicode[STIX]{x1D714}_{A}^{2}$
. We assume that
![]() $U$
is small far from
$U$
is small far from
![]() $r_{s}$
, but sufficiently large close to this point.
$r_{s}$
, but sufficiently large close to this point.
To simplify the analysis we employ a safety factor which is constant
![]() $1/q=\unicode[STIX]{x1D707}_{0}$
for
$1/q=\unicode[STIX]{x1D707}_{0}$
for
![]() $0<r<r_{0}$
and
$0<r<r_{0}$
and
![]() $1/q=\unicode[STIX]{x1D707}_{\ast }\sim n/m_{0}<\unicode[STIX]{x1D707}_{0}$
for
$1/q=\unicode[STIX]{x1D707}_{\ast }\sim n/m_{0}<\unicode[STIX]{x1D707}_{0}$
for
![]() $r_{\ast }<r<a$
, while in the region
$r_{\ast }<r<a$
, while in the region
![]() $r_{0}<r<r_{\ast }$
behaves as (Brunetti et al.
Reference Brunetti, Graves, Lazzaro, Mariani, Nowak, Cooper and Wahlberg2018):
$r_{0}<r<r_{\ast }$
behaves as (Brunetti et al.
Reference Brunetti, Graves, Lazzaro, Mariani, Nowak, Cooper and Wahlberg2018):
This corresponds to a current profile of the form (the profiles for
![]() $q$
and
$q$
and
![]() $J_{0}$
are shown in figure 5):
$J_{0}$
are shown in figure 5):
 $$\begin{eqnarray}\displaystyle \displaystyle R_{0}J_{0}=\left\{\begin{array}{@{}ll@{}}2\unicode[STIX]{x1D707}_{0}, & 0<r<r_{0}\\ 0, & r_{0}<r<r_{\ast },\\ 2\unicode[STIX]{x1D707}_{\ast }, & r_{\ast }<r<a,\end{array}\right. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle R_{0}J_{0}=\left\{\begin{array}{@{}ll@{}}2\unicode[STIX]{x1D707}_{0}, & 0<r<r_{0}\\ 0, & r_{0}<r<r_{\ast },\\ 2\unicode[STIX]{x1D707}_{\ast }, & r_{\ast }<r<a,\end{array}\right. & & \displaystyle\end{eqnarray}$$

Figure 5. Step current model: the
![]() $q$
profile is assumed parabolic (i.e. vanishing current) for
$q$
profile is assumed parabolic (i.e. vanishing current) for
![]() $r_{0}<r<r_{\ast }$
.
$r_{0}<r<r_{\ast }$
.
In the region
![]() $r_{0}<r<r_{\ast }$
, sufficiently far from
$r_{0}<r<r_{\ast }$
, sufficiently far from
![]() $r_{s}$
we neglect the terms proportional to
$r_{s}$
we neglect the terms proportional to
![]() $\unicode[STIX]{x1D6FE}$
, hence the solution of (B 1) reads:
$\unicode[STIX]{x1D6FE}$
, hence the solution of (B 1) reads:
where
![]() $K_{\lessgtr }$
and
$K_{\lessgtr }$
and
![]() $T_{\lessgtr }$
are constants and the integrals in the expression above can be easily represented in terms of the Gauss hypergeometric function. Note that a more careful treatment is needed when
$T_{\lessgtr }$
are constants and the integrals in the expression above can be easily represented in terms of the Gauss hypergeometric function. Note that a more careful treatment is needed when
![]() $m$
is even.
$m$
is even.
When the resonant surface is approached we have:
 $$\begin{eqnarray}\displaystyle \displaystyle X_{-}(r\lessgtr r_{s}) & = & \displaystyle \pm {\displaystyle \frac{(K_{\lessgtr }+T_{\lessgtr })}{2n|\hat{x}|}}-{\displaystyle \frac{K_{\lessgtr }(1/2-m)+T_{\lessgtr }(1/2+m)}{2n}}-{\displaystyle \frac{U}{4n^{2}r_{s}}}\ln |\hat{x}|\nonumber\\ \displaystyle \displaystyle & & \displaystyle \mp {\displaystyle \frac{U}{4m^{2}n^{2}r_{s}|\hat{x}|}}-{\displaystyle \frac{U}{4n^{2}r_{s}}}\left(\unicode[STIX]{x1D6FE}_{E}-1+\ln 2+\unicode[STIX]{x1D6F9}\left({\displaystyle \frac{m}{2}}\right)+{\displaystyle \frac{1}{m}}-{\displaystyle \frac{1}{2m^{2}}}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle X_{-}(r\lessgtr r_{s}) & = & \displaystyle \pm {\displaystyle \frac{(K_{\lessgtr }+T_{\lessgtr })}{2n|\hat{x}|}}-{\displaystyle \frac{K_{\lessgtr }(1/2-m)+T_{\lessgtr }(1/2+m)}{2n}}-{\displaystyle \frac{U}{4n^{2}r_{s}}}\ln |\hat{x}|\nonumber\\ \displaystyle \displaystyle & & \displaystyle \mp {\displaystyle \frac{U}{4m^{2}n^{2}r_{s}|\hat{x}|}}-{\displaystyle \frac{U}{4n^{2}r_{s}}}\left(\unicode[STIX]{x1D6FE}_{E}-1+\ln 2+\unicode[STIX]{x1D6F9}\left({\displaystyle \frac{m}{2}}\right)+{\displaystyle \frac{1}{m}}-{\displaystyle \frac{1}{2m^{2}}}\right),\end{eqnarray}$$
where
![]() $\hat{x}=(r-r_{s})/r_{s}$
. Far from
$\hat{x}=(r-r_{s})/r_{s}$
. Far from
![]() $r_{s}$
, neglecting the term proportional to
$r_{s}$
, neglecting the term proportional to
![]() $U$
,
$U$
,
![]() $K_{{<}}$
is expressed in terms of
$K_{{<}}$
is expressed in terms of
![]() $T_{{<}}$
by imposing smoothness at
$T_{{<}}$
by imposing smoothness at
![]() $r_{0}$
(if
$r_{0}$
(if
![]() $r_{0}\ll r_{\ast }$
and
$r_{0}\ll r_{\ast }$
and
![]() $m_{0}$
sufficiently large we can approximate
$m_{0}$
sufficiently large we can approximate
![]() $K_{{<}}\approx 0$
). If the inertial layer is thin, we may assume that the poloidal flux
$K_{{<}}\approx 0$
). If the inertial layer is thin, we may assume that the poloidal flux
![]() $\unicode[STIX]{x1D713}_{-}\sim \hat{x}X_{-}$
is continuous across
$\unicode[STIX]{x1D713}_{-}\sim \hat{x}X_{-}$
is continuous across
![]() $r_{s}$
. This implies that
$r_{s}$
. This implies that
![]() $(K_{{<}}+T_{{<}})=(K_{{>}}+T_{{>}})$
. The part of (B 5) which does not contain the logarithm can be written as:
$(K_{{<}}+T_{{<}})=(K_{{>}}+T_{{>}})$
. The part of (B 5) which does not contain the logarithm can be written as:
where we defined:
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6E5}_{\pm }=\pm {\displaystyle \frac{{\displaystyle \frac{1}{2}}+m+\left({\displaystyle \frac{1/2-m}{1/2+m}}\right){\displaystyle \frac{K_{\lessgtr }}{T_{\lessgtr }}}+{\displaystyle \frac{U/T_{\lessgtr }}{2m^{2}nr_{s}}}\mathscr{H}}{1+{\displaystyle \frac{K_{\lessgtr }}{T_{\lessgtr }}}-{\displaystyle \frac{U/T_{\lessgtr }}{2m^{2}nr_{s}}}}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6E5}_{\pm }=\pm {\displaystyle \frac{{\displaystyle \frac{1}{2}}+m+\left({\displaystyle \frac{1/2-m}{1/2+m}}\right){\displaystyle \frac{K_{\lessgtr }}{T_{\lessgtr }}}+{\displaystyle \frac{U/T_{\lessgtr }}{2m^{2}nr_{s}}}\mathscr{H}}{1+{\displaystyle \frac{K_{\lessgtr }}{T_{\lessgtr }}}-{\displaystyle \frac{U/T_{\lessgtr }}{2m^{2}nr_{s}}}}}, & \displaystyle\end{eqnarray}$$
with
![]() $\mathscr{H}=m^{2}[\unicode[STIX]{x1D6FE}_{E}-1+\ln 2+\unicode[STIX]{x1D6F9}(m/2)]+m-1/2$
.
$\mathscr{H}=m^{2}[\unicode[STIX]{x1D6FE}_{E}-1+\ln 2+\unicode[STIX]{x1D6F9}(m/2)]+m-1/2$
.
In the inertial layer we approximate (B 1) as:
where
![]() $\bar{\unicode[STIX]{x1D6FE}}^{2}=\unicode[STIX]{x1D6FE}^{2}(1+2q^{2})/(\unicode[STIX]{x1D714}_{A}mr_{s}\unicode[STIX]{x1D707}_{s}^{\prime })^{2}$
and
$\bar{\unicode[STIX]{x1D6FE}}^{2}=\unicode[STIX]{x1D6FE}^{2}(1+2q^{2})/(\unicode[STIX]{x1D714}_{A}mr_{s}\unicode[STIX]{x1D707}_{s}^{\prime })^{2}$
and
![]() $U_{1}=(1/r_{s})U/(mr_{s}\unicode[STIX]{x1D707}_{s}^{\prime })^{2}$
. The solution of (B 8) is
$U_{1}=(1/r_{s})U/(mr_{s}\unicode[STIX]{x1D707}_{s}^{\prime })^{2}$
. The solution of (B 8) is
![]() $X_{-}=c_{0}+c_{1}\arctan (\hat{x}/\bar{\unicode[STIX]{x1D6FE}})-(U_{1}/2)\ln (\hat{x}^{2}+\bar{\unicode[STIX]{x1D6FE}}^{2})$
, where
$X_{-}=c_{0}+c_{1}\arctan (\hat{x}/\bar{\unicode[STIX]{x1D6FE}})-(U_{1}/2)\ln (\hat{x}^{2}+\bar{\unicode[STIX]{x1D6FE}}^{2})$
, where
![]() $d_{0,1}$
are constants of integration. The logarithmic terms in (B 5) and in the solution of (B 8) are automatically matched. If
$d_{0,1}$
are constants of integration. The logarithmic terms in (B 5) and in the solution of (B 8) are automatically matched. If
![]() $\hat{x}/\bar{\unicode[STIX]{x1D6FE}}\rightarrow \infty$
, the asymptotic behaviour of the non-logarithmic part of the layer solution behaves as (A 5). Matching gives
$\hat{x}/\bar{\unicode[STIX]{x1D6FE}}\rightarrow \infty$
, the asymptotic behaviour of the non-logarithmic part of the layer solution behaves as (A 5). Matching gives
![]() $\unicode[STIX]{x03C0}/\hat{\unicode[STIX]{x1D6FE}}+\unicode[STIX]{x1D6E5}_{+}+\unicode[STIX]{x1D6E5}_{-}=0$
(see previous section).
$\unicode[STIX]{x03C0}/\hat{\unicode[STIX]{x1D6FE}}+\unicode[STIX]{x1D6E5}_{+}+\unicode[STIX]{x1D6E5}_{-}=0$
(see previous section).










