1. INTRODUCTION
Navigation technology for obtaining a probe's position, velocity and attitude, is one of the key technologies for deep-space missions, especially during the approach phase. Many deep-space probes have been launched and many navigation methods for deep-space probes have been developed (Zhang and Xu, Reference Zhang and Xu2016). The method that is used most often is ground-based radio navigation, which is performed on the ground using radiometric data and on board image data when required (Prestage and Weaver, Reference Prestage and Weaver2007). The Messager orbiter obtained a 10 km uncertainty in the B-plane before its Mercury encounter using radiometric data, landmark and laser altimeter data. Rosetta achieved 2·6 km off its nominal value in the B-plane by using optical image and radiometric data (Stanbridge et al., Reference Stanbridge, Miller, Carranza, Williams, Williams and Wolff2009). The New Horizon, a Pluto explorer, was launched on 19 January 2006, and the expected accuracy during approach is 10 km (Stanbridge et al., Reference Stanbridge, Miller, Carranza, Williams, Williams and Wolff2009).
However, traditional ground-based navigation suffers from many limitations such as high cost, a long time delay and discontinuity. Autonomous navigation is a preferable choice that can increase the navigation frequency and save communication resources (Crouse et al., Reference Crouse, Zanetti, D'Souza and Spanos2009), especially during the probe's approach phase (Ma et al., Reference Ma, Jiang and Baoyin2015). Celestial Navigation Systems (CNS) are a type of autonomous navigation technology that have been widely used in deep-space missions, such as Deep Space 1 (Riedel et al., Reference Riedel, Bhaskaran, Synnott, Desai, Bollman, Dumont, Halsell, Han, Kennedy, Null, Owen, Werner and Williams1997), Deep Impact (Frauenholz et al., Reference Frauenholz, Bhat, Chesley, Mastrodemos, Owen and Ryne2008), Stardust (Bhaskaran et al., Reference Bhaskaran, Riedel and Synnott1998b), and others (Mastrodemos et al., Reference Mastrodemos, Kubitschek and Synnott2005; Gillam et al., Reference Gillam, Owen, Vaughan, Wang, Costello, Jacobson, Bluhm, Pojman and Ionasescu2008). The CNS for Deep Space 1 is the first validated deep-space autonomous navigation system, and it was evaluated by the Deep Space Network (DSN) and by means of ground processing (Bhaskaran et al., Reference Bhaskaran, Desai, Dumont, Kennedy, Null, Owen, Riedel, Synnott and Werner1998a). It is anticipated that there is great potential for autonomous CNSs (Owen et al., Reference Owen, Duxbury, Acton, Synnott, Riedel and Bhaskaran2008).
In CNSs, the filter method is usually used to estimate the position and velocity of the probe, usually using an orbit dynamic equation as the state model and the angles between Mars, Phobos, Deimos and their background stars as measurements. In the state model, the reference positions of celestial bodies are given by the ephemeris. For the CNS of a Mars probe, previous research has shown that a Mars ephemeris error can greatly affect the dynamic model, especially during the Mars approach phase (Standish, Reference Standish2002; Ma et al., Reference Ma, Ning and Fang2012). As the measurements are usually based on the observation of Mars, Phobos, Deimos and the stars, ephemeris errors will also affect the measurement model. As a consequence, the ephemeris errors of Mars, Phobos and Deimos will affect the navigation result of the CNS during the Mars approach phase.
Many research studies have been carried out on the ephemerides of Mars, Phobos and Deimos. The three main ephemerides of planets are the Development Ephemeris series (DE-series), the Ephemerides of Planets and the Moon series (EPM-series) (Pitjeva, Reference Pitjeva2005) and Integration Numérique Planétaire de l'Observatoire de Paris (INPOP-series ephemeris) (Kudryavtsev, Reference Kudryavtsev2011; Fienga et al., Reference Fienga, Laskar, Simon, Manche and Gastineau2004). The one that is most often used is the DE-series which was released by the Jet Propulsion Laboratory (JPL). Research by Deng et al. (Reference Deng, Fan and Xie2014) has shown that the difference between DE421 and DE405 is about 1 km, and this gives the characteristics of the Mars ephemeris error. The orbits and ephemerides of Phobos and Deimos have also been studied widely. Research by Jacobson and Lainey (Reference Jacobson and Lainey2014) has shown that the ephemeris errors of Phobos and Deimos will be lower than 2 km until 2025, but they will reach about 8 km and 25 km respectively in 2050 (Jacobson, Reference Jacobson2010). These research studies have also shown that the ephemeris errors of Phobos and Deimos are periodical, which gives the uncertainty of the ephemerides. As mentioned above, the ephemeris errors of Mars, Phobos and Deimos and their influence on CNS cannot be neglected. Several research studies have been carried out on the influence of the Mars ephemeris error on the dynamic model of the Mars probe, but few research studies have been carried out on the influence of the ephemeris errors on CNSs. Thus, this paper analyses the ephemeris errors of Mars, Phobos and Deimos and their influence on CNSs during the Mars approach phase.
This paper analyses the ephemeris errors of Mars, Deimos and Phobos first by theory and simulation. It states that the ephemeris error of Mars is slowly-varying, and that the ephemeris errors of Phobos and Deimos are periodical during the Mars approach phase. Then, the system models of CNS are introduced simply. In deep-space CNS, system models that use the Sun as the central body are usually used. However, during the approach phase, the gravity of Mars becomes larger than that of the Sun. Thus, system models that use Mars as the central body are also available. This paper introduces both kinds of models, and analyses the influence of the ephemeris error of Mars on CNS using the two models. The influence of the Mars ephemeris error is analysed according to theoretical analysis and simulations. In the Sun-centred frame, the position error caused by the ephemeris error of Mars is equal to the ephemeris error itself, and the velocity error is slightly affected by the ephemeris error of Mars. In the Mars-centred frame, the position and velocity errors are hardly affected by the ephemeris error of Mars. The influences of the ephemeris errors of Phobos and Deimos are also analysed using two different orbits. The simulations state that the influences of the ephemeris errors of Phobos and Deimos are much greater than those of Mars. The navigation errors are affected by both the quantities and the periodicities of the ephemeris errors of Phobos and Deimos, and they change rapidly with the quantities of the ephemeris errors. The influences of the three directions are quite different, and depend on the coordinates of the orbit in the three directions. The influence on different orbits also differs. Finally, we also assess whether the CNS can reach the requirements of navigation during the approach phase. The analysis shows that a CNS with normal ephemeris errors is totally sufficient for navigation during the Mars approach phase, but larger ephemeris errors can easily spoil the navigation accuracy. Thus it is necessary to improve the ephemerides accuracies and reduce their influence on the CNS.
This paper is organised in six sections. After this introduction, the ephemeris errors of Mars, Phobos and Deimos and their characteristics are described in Section 2. The basic principles of CNS in the Sun-centred inertial frame and the Mars-centred inertial frame during the Mars approach phase are introduced in Section 3. The analysis of the influence of the Mars ephemeris error on the CNS during the Mars approach phase is presented in Section 4. Simulations and analysis are shown in Section 5 and conclusions are drawn in Section 6.
2. EPHEMERIS ERROR DURING THE MARS APPROACH PHASE
2.1. Mars Ephemeris Error
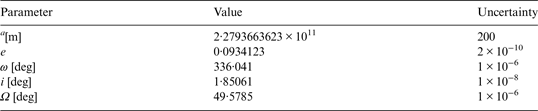
The position errors of Mars can be obtained with the orbit parameters and their uncertainties. The orbit parameters and uncertainties in the Sun-centred ecliptic frame (J2000) are shown in Table 1 (Folkner et al., Reference Folkner, Williams and Boggs2008).
Table 1. Orbit Parameters and Uncertainties of Mars.
Using the orbit parameters shown in Table 1, the ephemeris of Mars from 30 June 1997 00:00:00·000 to 6 July 1997 00:00:00·000 are shown in Figure 1. From Figure 1 we can see that the position errors of Mars in the x, y and z directions change slowly, which can be seen as slowly-varying values over a short period.

Figure 1. Ephemeris errors of Mars.
2.2. Ephemeris Errors of Phobos and Deimos
The position errors of Phobos and Deimos can also be obtained by means of their orbit parameters and their uncertainties. According to the research of Jacobson (Reference Jacobson2008), the orbit parameters and uncertainties of Phobos and Deimos, which are referred to the local Laplace plane, are shown in Table 2.
Table 2. Orbit Parameters and Uncertainties of Phobos and Deimos.

The position errors of Phobos and Deimos from 30 June 1997 00:00:00·000 to 6 July 1997 15:00:00·000 are shown in Figure 2. As we can see from Figure 2, the position errors of Phobos and Deimos are periodical, and their periods are equal to their orbit periods.

Figure 2. Position errors of Phobos (a) and Deimos (b) in the local Laplace plane.
Figure 2 shows the position errors of Phobos and Deimos in the local Laplace plane frame. However, the navigation frame in this paper is the Mars-centred mean ecliptic frame (J2000). Thus it is necessary to transform the position errors to the Mars-centred mean ecliptic frame. The transformation matrix can be calculated by the inclination and ascending node of the local Laplace plane referred to the mean ecliptic plane. As the local Laplace planes of Phobos and Deimos are near to the equator of Mars, the transformation from the Laplace planes to the mean ecliptic plane can be simplified as the transformation from the equator plane of Mars to the mean ecliptic plane. The transformation matrix can be calculated in two parts as shown in Figure 3. The first part is the transformation from the Mars equator frame (OX e Y e Z e ) to the Mars orbit frame (OX o Y o Z o ), and the second part is the transformation from the Mars orbit frame to the Mars ecliptic frame (OX i Y i Z i ).
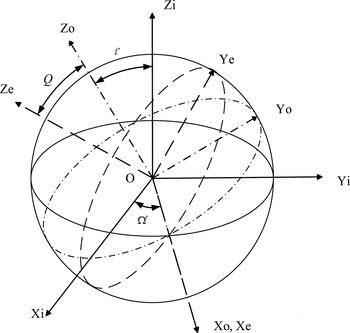
Figure 3. Transformation between Mars equator frame and Mars ecliptic frame.
As shown in Figure 3, the transformation matrix from OX e Y e Z e to OX o Y o Z o is
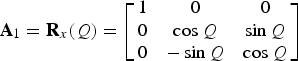 $${\bf A}_1 = {\bf R}_x (Q) = \left[ {\matrix{ 1 & 0 & 0 \cr 0 & {\cos Q} & {\sin Q} \cr 0 & { - \sin Q} & {\cos Q} \cr}} \right]$$
$${\bf A}_1 = {\bf R}_x (Q) = \left[ {\matrix{ 1 & 0 & 0 \cr 0 & {\cos Q} & {\sin Q} \cr 0 & { - \sin Q} & {\cos Q} \cr}} \right]$$
where Q is the obliquity of the Mars equator, and its value is about 23·28° (Jacobson and Lainey, Reference Jacobson and Lainey2014).
The transformation matrix from OX o Y o Z o to OX i Y i Z i is
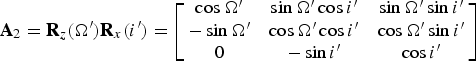 $${\bf A}_2 = {\bf R}_z (\Omega ^{\prime}){\bf R}_x (i^{\prime}) = \left[ {\matrix{ {\cos \Omega ^{\prime}} & {\sin \Omega ^{\prime}\cos i^{\prime}} & {\sin \Omega ^{\prime}\sin i^{\prime}} \cr { - \sin \Omega ^{\prime}} & {\cos \Omega ^{\prime}\cos i^{\prime}} & {\cos \Omega ^{\prime}\sin i^{\prime}} \cr 0 & { - \sin i^{\prime}} & {\cos i^{\prime}} \cr}} \right]$$
$${\bf A}_2 = {\bf R}_z (\Omega ^{\prime}){\bf R}_x (i^{\prime}) = \left[ {\matrix{ {\cos \Omega ^{\prime}} & {\sin \Omega ^{\prime}\cos i^{\prime}} & {\sin \Omega ^{\prime}\sin i^{\prime}} \cr { - \sin \Omega ^{\prime}} & {\cos \Omega ^{\prime}\cos i^{\prime}} & {\cos \Omega ^{\prime}\sin i^{\prime}} \cr 0 & { - \sin i^{\prime}} & {\cos i^{\prime}} \cr}} \right]$$
where Ω′ and i′ are the ascending node and inclination of Mars orbit, and their values are 49·58° and 1·85° (Jacobson, Reference Jacobson2008).
Then, the transformation matrix from OX e Y e Z e to OX i Y i Z i can be expressed as
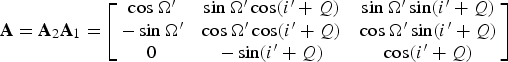 $${\bf A} = {\bf A}_2 {\bf A}_1 = \left[ {\matrix{ {\cos \Omega ^{\prime}} & {\sin \Omega ^{\prime}\cos (i^{\prime} + Q)} & {\sin \Omega ^{\prime}\sin (i^{\prime} + Q)} \cr { - \sin \Omega ^{\prime}} & {\cos \Omega ^{\prime}\cos (i^{\prime} + Q)} & {\cos \Omega ^{\prime}\sin (i^{\prime} + Q)} \cr 0 & { - \sin (i^{\prime} + Q)} & {\cos (i^{\prime} + Q)} \cr}} \right]$$
$${\bf A} = {\bf A}_2 {\bf A}_1 = \left[ {\matrix{ {\cos \Omega ^{\prime}} & {\sin \Omega ^{\prime}\cos (i^{\prime} + Q)} & {\sin \Omega ^{\prime}\sin (i^{\prime} + Q)} \cr { - \sin \Omega ^{\prime}} & {\cos \Omega ^{\prime}\cos (i^{\prime} + Q)} & {\cos \Omega ^{\prime}\sin (i^{\prime} + Q)} \cr 0 & { - \sin (i^{\prime} + Q)} & {\cos (i^{\prime} + Q)} \cr}} \right]$$
The position errors of Phobos and Deimos in the Mars ecliptic frame can be calculated by
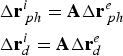 $$\eqalign{& \Delta {\bf r}_{\,ph}^i = {\bf A}\Delta {\bf r}_{\,ph}^e \cr & \Delta {\bf r}_d^i = {\bf A}\Delta {\bf r}_d^e} $$
$$\eqalign{& \Delta {\bf r}_{\,ph}^i = {\bf A}\Delta {\bf r}_{\,ph}^e \cr & \Delta {\bf r}_d^i = {\bf A}\Delta {\bf r}_d^e} $$
where
![]() $\Delta {\bf r}_{ph}^e $
and
$\Delta {\bf r}_{ph}^e $
and
![]() $\Delta {\bf r}_{ph}^e $
are the position errors of Phobos and Deimos in the equator frame of Mars, which are shown in Figure 2.
$\Delta {\bf r}_{ph}^e $
are the position errors of Phobos and Deimos in the equator frame of Mars, which are shown in Figure 2.
![]() $\Delta {\bf r}_{ph}^i $
and
$\Delta {\bf r}_{ph}^i $
and
![]() $\Delta {\bf r}_d^i $
are position errors in the ecliptic frame which can be calculated and shown, as in Figure 4.
$\Delta {\bf r}_d^i $
are position errors in the ecliptic frame which can be calculated and shown, as in Figure 4.

Figure 4. Position errors of Phobos (a) and Deimos (b) in the Mars ecliptic frame.
3. BASIC PRINCIPLE OF CNS
A filter method is usually used for CNSs during the Mars approach phase. The filter method uses the state model and measurement model to estimate the position and the velocity of the probe. In a deep-space mission, we usually use the Sun-centred inertial frame as the navigation frame. However, during the Mars approach phase, the position of the probe relative to Mars is required, and the level of Mars’ perturbation is similar to that of the Sun's. Thus there are two available system models for CNSs in this paper. One is expressed in the Sun-centred inertial frame with the Sun as the central body, and the other is expressed in the Mars-centred inertial frame with Mars as the central body. Both of these systems are given and analysed in this paper.
3.1. System Models in the Sun-centred inertial frame
During the Mars approach phase, the orbital motion of the probe can be seen as an n-body problem with the Sun as the central body. The dynamical model in the Sun-centred inertial frame (J2000.0) is written as
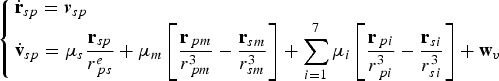 $$\left\{ {\matrix{ {{ \dot {\bf r}}_{sp} = {\bi v}_{sp}} \hfill \cr {{ \dot {\bf v}}_{sp} = \mu _s \displaystyle{{{\bf r}_{sp}} \over {r_{\,ps}^e}} + \mu _m \left[ {\displaystyle{{{\bf r}_{\,pm}} \over {r_{\,pm}^3}} - \displaystyle{{{\bf r}_{sm}} \over {r_{sm}^3}}} \right] + \sum\limits_{i = 1}^7 {\mu _i} \left[ {\displaystyle{{{\bf r}_{\,pi}} \over {r_{\,pi}^3}} - \displaystyle{{{\bf r}_{si}} \over {r_{si}^3}}} \right] + {\bf w}_v} \hfill \cr}} \right.$$
$$\left\{ {\matrix{ {{ \dot {\bf r}}_{sp} = {\bi v}_{sp}} \hfill \cr {{ \dot {\bf v}}_{sp} = \mu _s \displaystyle{{{\bf r}_{sp}} \over {r_{\,ps}^e}} + \mu _m \left[ {\displaystyle{{{\bf r}_{\,pm}} \over {r_{\,pm}^3}} - \displaystyle{{{\bf r}_{sm}} \over {r_{sm}^3}}} \right] + \sum\limits_{i = 1}^7 {\mu _i} \left[ {\displaystyle{{{\bf r}_{\,pi}} \over {r_{\,pi}^3}} - \displaystyle{{{\bf r}_{si}} \over {r_{si}^3}}} \right] + {\bf w}_v} \hfill \cr}} \right.$$
where
![]() ${\bf r}_{sp} $
and
${\bf r}_{sp} $
and
![]() ${\bf v}_{sp} $
are the position vector and the velocity vector of the probe relative to the Sun.
${\bf v}_{sp} $
are the position vector and the velocity vector of the probe relative to the Sun.
![]() ${\bf r}_{sm} $
is the position vector of Mars.
${\bf r}_{sm} $
is the position vector of Mars.
![]() ${\bf r}_{pm} = {\bf r}_{sm} - {\bf r}_{sp} $
is the position vector of the probe relative to Mars.
${\bf r}_{pm} = {\bf r}_{sm} - {\bf r}_{sp} $
is the position vector of the probe relative to Mars.
![]() ${\bf r}_{si} $
is the position vector of the planet i, which represents Mercury, Venus, Earth, Jupiter, Saturn, Uranus and Neptune, respectively.
${\bf r}_{si} $
is the position vector of the planet i, which represents Mercury, Venus, Earth, Jupiter, Saturn, Uranus and Neptune, respectively.
![]() ${\bf r}_{pi} = {\bf r}_{si} - {\bf r}_{sp} $
is the position vector of the probe relative to the planet i. μ
s
is the gravitational parameter (GM) constant of the Sun, μ
m
is the GM constant of Mars and μ
i
is the GM constant of the planet i.
${\bf r}_{pi} = {\bf r}_{si} - {\bf r}_{sp} $
is the position vector of the probe relative to the planet i. μ
s
is the gravitational parameter (GM) constant of the Sun, μ
m
is the GM constant of Mars and μ
i
is the GM constant of the planet i.
![]() ${\bf w}_v $
is the noise.
${\bf w}_v $
is the noise.
The measurements used in this study are angles between the Line Of Sight (LOS) of Mars, Deimos, Phobos and the stars as shown in Figure 5, and the measurement model is given by
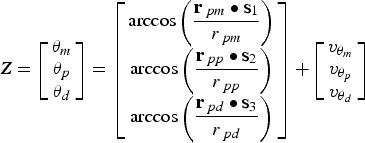 $${\bi Z} = \left[ {\matrix{ {\theta _m} \cr {\theta _p} \cr {\theta _d} \cr}} \right] = \left[ {\matrix{ {\arccos \left( {\displaystyle{{{\bf r}_{\,pm} \bullet {\bf s}_1} \over {r_{\,pm}}}} \right)} \cr {\arccos \left( {\displaystyle{{{\bf r}_{\,pp} \bullet {\bf s}_2} \over {r_{\,pp}}}} \right)} \cr {\arccos \left( {\displaystyle{{{\bf r}_{\,pd} \bullet {\bf s}_3} \over {r_{\,pd}}}} \right)} \cr}} \right] + \left[ {\matrix{ {v_{\theta _m}} \cr {v_{\theta _p}} \cr {v_{\theta _d}} \cr}} \right]$$
$${\bi Z} = \left[ {\matrix{ {\theta _m} \cr {\theta _p} \cr {\theta _d} \cr}} \right] = \left[ {\matrix{ {\arccos \left( {\displaystyle{{{\bf r}_{\,pm} \bullet {\bf s}_1} \over {r_{\,pm}}}} \right)} \cr {\arccos \left( {\displaystyle{{{\bf r}_{\,pp} \bullet {\bf s}_2} \over {r_{\,pp}}}} \right)} \cr {\arccos \left( {\displaystyle{{{\bf r}_{\,pd} \bullet {\bf s}_3} \over {r_{\,pd}}}} \right)} \cr}} \right] + \left[ {\matrix{ {v_{\theta _m}} \cr {v_{\theta _p}} \cr {v_{\theta _d}} \cr}} \right]$$
where
![]() ${\bf s}_1 $
,
${\bf s}_1 $
,
![]() ${\bf s}_2 $
,
${\bf s}_2 $
,
![]() ${\bf s}_3 $
are the position vectors of the navigation stars in the Sun-centred inertial frame, which are obtained from the star catalogue by star identification.
${\bf s}_3 $
are the position vectors of the navigation stars in the Sun-centred inertial frame, which are obtained from the star catalogue by star identification.
![]() ${\bf r}_{pp} $
and
${\bf r}_{pp} $
and
![]() ${\bf r}_{pd} $
are the position vectors of the probe relative to Phobos and Deimos respectively.
${\bf r}_{pd} $
are the position vectors of the probe relative to Phobos and Deimos respectively.

Figure 5. Diagram of measurements of the CNS.
3.2. System Models in the Mars-centred Inertial Frame
When the probe is approaching Mars, its orbit motion can also be seen as a perturbation motion with Mars as the central body. Thus, the expression of the probe's dynamic model given in the Mars-centred inertial frame is shown as follows.
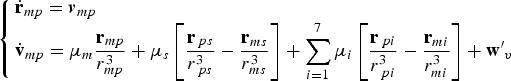 $$\left\{ {\matrix{ {{ \dot {\bf r}}_{mp} = {\bi v}_{mp}} \hfill \cr {{\dot {\bf v}}_{mp} = \mu _m \displaystyle{{{\bf r}_{mp}} \over {r_{mp}^3}} + \mu _s \left[ {\displaystyle{{{\bf r}_{\,ps}} \over {r_{\,ps}^3}} - \displaystyle{{{\bf r}_{ms}} \over {r_{ms}^3}}} \right] + \sum\limits_{i = 1}^7 {\mu _i \left[ {\displaystyle{{{\bf r}_{\,pi}} \over {r_{\,pi}^3}} - \displaystyle{{{\bf r}_{mi}} \over {r_{mi}^3}}} \right] + {{\bf w}^{\prime}}_v}} \hfill \cr}} \right.$$
$$\left\{ {\matrix{ {{ \dot {\bf r}}_{mp} = {\bi v}_{mp}} \hfill \cr {{\dot {\bf v}}_{mp} = \mu _m \displaystyle{{{\bf r}_{mp}} \over {r_{mp}^3}} + \mu _s \left[ {\displaystyle{{{\bf r}_{\,ps}} \over {r_{\,ps}^3}} - \displaystyle{{{\bf r}_{ms}} \over {r_{ms}^3}}} \right] + \sum\limits_{i = 1}^7 {\mu _i \left[ {\displaystyle{{{\bf r}_{\,pi}} \over {r_{\,pi}^3}} - \displaystyle{{{\bf r}_{mi}} \over {r_{mi}^3}}} \right] + {{\bf w}^{\prime}}_v}} \hfill \cr}} \right.$$
where
![]() ${\bf r}_{mp} $
and
${\bf r}_{mp} $
and
![]() ${\bf v}_{mp} $
are the position and velocity vectors of the probe relative to Mars.
${\bf v}_{mp} $
are the position and velocity vectors of the probe relative to Mars.
![]() ${\bf r}_{ms} $
is the position vector of the Sun relative to Mars.
${\bf r}_{ms} $
is the position vector of the Sun relative to Mars.
![]() ${\bf r}_{ps} = {\bf r}_{ms} - {\bf r}_{mp} $
is the position vector of the probe relative to the Sun.
${\bf r}_{ps} = {\bf r}_{ms} - {\bf r}_{mp} $
is the position vector of the probe relative to the Sun.
![]() ${\bf r}_{mi} $
is the position vector of the planet i relative to Mars, which represents Mercury, Venus, Earth, Jupiter, Saturn, Uranus and Neptune, respectively.
${\bf r}_{mi} $
is the position vector of the planet i relative to Mars, which represents Mercury, Venus, Earth, Jupiter, Saturn, Uranus and Neptune, respectively.
![]() ${\bf r}_{pi} = {\bf r}_{mi} - {\bf r}_{mp} $
is the position vector of the probe relative to the planet i.
${\bf r}_{pi} = {\bf r}_{mi} - {\bf r}_{mp} $
is the position vector of the probe relative to the planet i.
The measurement model in the Mars-centred inertial frame is similar to the model in the Sun-centred inertial frame, as shown in Equation (6). The difference is that
![]() ${\bf r}_{pm} $
,
${\bf r}_{pm} $
,
![]() ${\bf r}_{pd} $
,
${\bf r}_{pd} $
,
![]() ${\bf r}_{pp} $
and
${\bf r}_{pp} $
and
![]() ${\bf s}_1 $
,
${\bf s}_1 $
,
![]() ${\bf s}_2 $
,
${\bf s}_2 $
,
![]() ${\bf s}_3 $
are expressed in the Mars-centred inertial frame.
${\bf s}_3 $
are expressed in the Mars-centred inertial frame.
3.3. Filter Method
The process and measurement model of CNS is usually nonlinear as shown above. To solve this problem, the Unscented Kalman Filter (UKF) (Julier and Uhlmann, Reference Julier and Uhlmann1997) is used in this paper.
4. INFLUENCE OF THE MARS EPHEMERIS ERROR ON THE CNS DURING THE MARS APPROACH PHASE
This section provides a simple analysis of the influence of the Mars ephemeris error in two different frames. At first, in the Sun-centred inertial frame, the ephemeris gives the reference position of Mars. The accuracy of Mars’ ephemeris affects the accuracy of
![]() ${\bf r}_{sm} $
but also affects the accuracy of
${\bf r}_{sm} $
but also affects the accuracy of
![]() ${\bf r}_{pm} $
as a consequence. Thus, the ephemeris error affects the accuracy of the state model. Furthermore, from Equation (6) we can see that the accuracy of the measurement model also depends on the accuracy of the reference position of Mars, Deimos and Phobos. Therefore, the ephemeris error affects both the state model and the measurement model. Secondly, in the Mars-centred inertial frame, the Mars ephemeris error does not affect the measurement model, but in the state model, the Mars ephemeris error affects the reference position of the Sun and other planets. Thus, it is necessary to analyse the influence of the Mars ephemeris error.
${\bf r}_{pm} $
as a consequence. Thus, the ephemeris error affects the accuracy of the state model. Furthermore, from Equation (6) we can see that the accuracy of the measurement model also depends on the accuracy of the reference position of Mars, Deimos and Phobos. Therefore, the ephemeris error affects both the state model and the measurement model. Secondly, in the Mars-centred inertial frame, the Mars ephemeris error does not affect the measurement model, but in the state model, the Mars ephemeris error affects the reference position of the Sun and other planets. Thus, it is necessary to analyse the influence of the Mars ephemeris error.
4.1. Influence of the Mars Ephemeris Error on the CNS in the Sun-centred Inertial Frame
We assume that in the Sun-centred inertial frame, the position estimation and the velocity estimation of the probe are
![]() ${ \tilde {\bf r}}_{sp} $
and
${ \tilde {\bf r}}_{sp} $
and
![]() ${ \tilde {\bf v}}_{sp} $
, when the Mars ephemeris with error is used. According to Equation (5),
${ \tilde {\bf v}}_{sp} $
, when the Mars ephemeris with error is used. According to Equation (5),
![]() ${ \tilde {\bf r}}_{sp} $
and
${ \tilde {\bf r}}_{sp} $
and
![]() ${ \tilde {\bf v}}_{sp} $
conform to the equation shown as follows.
${ \tilde {\bf v}}_{sp} $
conform to the equation shown as follows.
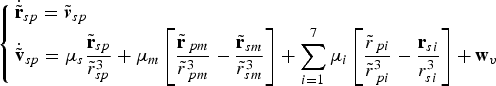 $$\left\{ {\matrix{ {{ \dot {\tilde {\bf r}}}_{sp} = { \tilde {\bi v}}_{sp}} \hfill \cr {{ \dot {\tilde {\bf v}}}_{sp} = \mu _s \displaystyle{{{ \tilde {\bf r}}_{sp}} \over {{\tilde r}_{sp}^3}} + \mu _m \left[ {\displaystyle{{{ \tilde {\bf r}}_{\,pm}} \over {{\tilde r}_{\,pm}^3}} - \displaystyle{{{ \tilde {\bf r}}_{sm}} \over {{\tilde r}_{sm}^3}}} \right] + \sum\limits_{i = 1}^7 {\mu _i \left[ {\displaystyle{{{ \tilde r}_{\,pi}} \over {{\tilde r}_{\,pi}^3}} - \displaystyle{{{\bf r}_{si}} \over {r_{si}^3}}} \right] + {\bf {\bf w}}_v}} \hfill \cr}} \right.$$
$$\left\{ {\matrix{ {{ \dot {\tilde {\bf r}}}_{sp} = { \tilde {\bi v}}_{sp}} \hfill \cr {{ \dot {\tilde {\bf v}}}_{sp} = \mu _s \displaystyle{{{ \tilde {\bf r}}_{sp}} \over {{\tilde r}_{sp}^3}} + \mu _m \left[ {\displaystyle{{{ \tilde {\bf r}}_{\,pm}} \over {{\tilde r}_{\,pm}^3}} - \displaystyle{{{ \tilde {\bf r}}_{sm}} \over {{\tilde r}_{sm}^3}}} \right] + \sum\limits_{i = 1}^7 {\mu _i \left[ {\displaystyle{{{ \tilde r}_{\,pi}} \over {{\tilde r}_{\,pi}^3}} - \displaystyle{{{\bf r}_{si}} \over {r_{si}^3}}} \right] + {\bf {\bf w}}_v}} \hfill \cr}} \right.$$
where
![]() ${ \tilde {\bf r}}_{pm} = { \tilde {\bf r}}_{sm} - { \tilde {\bf r}}_{sp} $
and
${ \tilde {\bf r}}_{pm} = { \tilde {\bf r}}_{sm} - { \tilde {\bf r}}_{sp} $
and
![]() ${ \tilde {\bf r}}_{pi} = { \tilde {\bf r}}_{si} - { \tilde {\bf r}}_{sp} $
.
${ \tilde {\bf r}}_{pi} = { \tilde {\bf r}}_{si} - { \tilde {\bf r}}_{sp} $
.
![]() ${ \tilde {\bf r}}_{sm} = {\bf r}_{sm} + \Delta {\bf r}_{sm} $
is the position vector of Mars with error.
${ \tilde {\bf r}}_{sm} = {\bf r}_{sm} + \Delta {\bf r}_{sm} $
is the position vector of Mars with error.
Assuming
![]() ${ \tilde {\bf r}}_{sp} = { \bar {\bf r}}_{sp} + \Delta {\bf r}_{sm} $
, we have
${ \tilde {\bf r}}_{sp} = { \bar {\bf r}}_{sp} + \Delta {\bf r}_{sm} $
, we have
![]() ${ \tilde {\bf r}}_{pm} = { \tilde {\bf r}}_{sm} - { \tilde {\bf r}}_{sp} = {\bf r}_{sm} - { \bar {\bf r}}_{sp} = { \bar {\bf r}}_{pm} $
and
${ \tilde {\bf r}}_{pm} = { \tilde {\bf r}}_{sm} - { \tilde {\bf r}}_{sp} = {\bf r}_{sm} - { \bar {\bf r}}_{sp} = { \bar {\bf r}}_{pm} $
and
![]() ${ \tilde {\bf r}}_{pi} = {\bf r}_{si} - { \tilde {\bf r}}_{sp} = { \bar {\bf r}}_{pi} - \Delta {\bf r}_{sm} $
as shown in Figure 6. Because
${ \tilde {\bf r}}_{pi} = {\bf r}_{si} - { \tilde {\bf r}}_{sp} = { \bar {\bf r}}_{pi} - \Delta {\bf r}_{sm} $
as shown in Figure 6. Because
![]() $\Delta {\bf r}_{sm} $
is a slow varying vector,
$\Delta {\bf r}_{sm} $
is a slow varying vector,
![]() ${ \bar {\bf v}}_{sp} = { \dot {\bar {\bf r}}}_{sp} = { \dot {\tilde {\bf r}}}_{sp} - \Delta { \dot {\bf r}}_{sm} = { \tilde {\bf v}}_{sp} - \Delta { \dot {\bf r}}_{sm} $
. Substituting
${ \bar {\bf v}}_{sp} = { \dot {\bar {\bf r}}}_{sp} = { \dot {\tilde {\bf r}}}_{sp} - \Delta { \dot {\bf r}}_{sm} = { \tilde {\bf v}}_{sp} - \Delta { \dot {\bf r}}_{sm} $
. Substituting
![]() ${ \tilde {\bf r}}_{sp} $
with
${ \tilde {\bf r}}_{sp} $
with
![]() ${ \bar {\bf r}}_{sp} + \Delta {\bf r}_{sm} $
, we have
${ \bar {\bf r}}_{sp} + \Delta {\bf r}_{sm} $
, we have
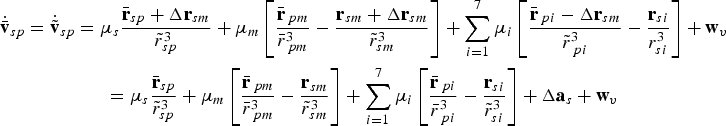 $$\displaylines{{ \dot {\bar {\bf v}}}_{sp} = { \dot {\tilde {\bf v}}}_{sp} = \mu _s \displaystyle{{{ \bar {\bf r}}_{sp} + \Delta {\bf r}_{sm}} \over {{\tilde r}_{sp}^3}} + \mu _m \left[ {\displaystyle{{{ \bar {\bf r}}_{\,pm}} \over {\bar r_{\,pm}^3}} - \displaystyle{{{\bf r}_{sm} + \Delta {\bf r}_{sm}} \over {{\tilde r}_{sm}^3}}} \right] + \sum\limits_{i = 1}^7 {\mu _i \left[ {\displaystyle{{{ \bar {\bf r}}_{\,pi} - \Delta {\bf r}_{sm}} \over {{\tilde r}_{\,pi}^3}} - \displaystyle{{{\bf r}_{si}} \over {r_{si}^3}}} \right] + {\bf w}_v} \cr = \mu _s \displaystyle{{{ \bar {\bf r}}_{sp}} \over {{\tilde r}_{sp}^3}} + \mu _m \left[ {\displaystyle{{{ \bar {\bf r}}_{\,pm}} \over {\bar r_{\,pm}^3}} - \displaystyle{{{\bf r}_{sm}} \over {{\tilde r}_{sm}^3}}} \right] + \sum\limits_{i = 1}^7 {\mu _i \left[ {\displaystyle{{{ \bar {\bf r}}_{\,pi}} \over {\bar r_{\,pi}^3}} - \displaystyle{{{\bf r}_{si}} \over {{\tilde r}_{si}^3}}} \right] + \Delta {\bf a}_s + {\bf w}_v}} $$
$$\displaylines{{ \dot {\bar {\bf v}}}_{sp} = { \dot {\tilde {\bf v}}}_{sp} = \mu _s \displaystyle{{{ \bar {\bf r}}_{sp} + \Delta {\bf r}_{sm}} \over {{\tilde r}_{sp}^3}} + \mu _m \left[ {\displaystyle{{{ \bar {\bf r}}_{\,pm}} \over {\bar r_{\,pm}^3}} - \displaystyle{{{\bf r}_{sm} + \Delta {\bf r}_{sm}} \over {{\tilde r}_{sm}^3}}} \right] + \sum\limits_{i = 1}^7 {\mu _i \left[ {\displaystyle{{{ \bar {\bf r}}_{\,pi} - \Delta {\bf r}_{sm}} \over {{\tilde r}_{\,pi}^3}} - \displaystyle{{{\bf r}_{si}} \over {r_{si}^3}}} \right] + {\bf w}_v} \cr = \mu _s \displaystyle{{{ \bar {\bf r}}_{sp}} \over {{\tilde r}_{sp}^3}} + \mu _m \left[ {\displaystyle{{{ \bar {\bf r}}_{\,pm}} \over {\bar r_{\,pm}^3}} - \displaystyle{{{\bf r}_{sm}} \over {{\tilde r}_{sm}^3}}} \right] + \sum\limits_{i = 1}^7 {\mu _i \left[ {\displaystyle{{{ \bar {\bf r}}_{\,pi}} \over {\bar r_{\,pi}^3}} - \displaystyle{{{\bf r}_{si}} \over {{\tilde r}_{si}^3}}} \right] + \Delta {\bf a}_s + {\bf w}_v}} $$
where
![]() $\Delta {\bf a}_s $
is the extra perturbation caused by Mars ephemeris error
$\Delta {\bf a}_s $
is the extra perturbation caused by Mars ephemeris error
![]() $\Delta {\bf r}_{sm} $
. The equation of
$\Delta {\bf r}_{sm} $
. The equation of
![]() $\Delta {\bf a}_s $
is shown as
$\Delta {\bf a}_s $
is shown as
 $$\Delta {\bf a}_s = \mu _s \displaystyle{{\Delta {\bf r}_{sm}} \over {{\tilde r}_{sp}^4}} - \mu _m \displaystyle{{\Delta {\bf r}_{sm}} \over {{\tilde r}_{sm}^3}} - \sum\limits_{i = 1}^7 {\mu _i} \displaystyle{{\Delta {\bf r}_{sm}} \over {{\tilde r}_{\,pi}^3}} $$
$$\Delta {\bf a}_s = \mu _s \displaystyle{{\Delta {\bf r}_{sm}} \over {{\tilde r}_{sp}^4}} - \mu _m \displaystyle{{\Delta {\bf r}_{sm}} \over {{\tilde r}_{sm}^3}} - \sum\limits_{i = 1}^7 {\mu _i} \displaystyle{{\Delta {\bf r}_{sm}} \over {{\tilde r}_{\,pi}^3}} $$

Figure 6. Relationship between
![]() ${ \tilde {\bf r}}_{pm} $
,
${ \tilde {\bf r}}_{pm} $
,
![]() ${\bf r}_{pi} $
and
${\bf r}_{pi} $
and
![]() ${ \bar {\bf r}}_{pm} $
,
${ \bar {\bf r}}_{pm} $
,
![]() ${ \bar {\bf r}}_{pi} $
.
${ \bar {\bf r}}_{pi} $
.
Since
![]() $\Delta {\bf r}_{sm} \ll { \bar {\bf r}}_{sp} $
,
$\Delta {\bf r}_{sm} \ll { \bar {\bf r}}_{sp} $
,
![]() ${\bf r}_{sm} $
,
${\bf r}_{sm} $
,
![]() ${ \bar {\bf r}}_{pi} $
during Mars approach phase,
${ \bar {\bf r}}_{pi} $
during Mars approach phase,
![]() $\Delta {\bf a}_s $
can be ignored and
$\Delta {\bf a}_s $
can be ignored and
![]() ${ \tilde {\bf r}}_{sp} \approx { \bar {\bf r}}_{sp} $
,
${ \tilde {\bf r}}_{sp} \approx { \bar {\bf r}}_{sp} $
,
![]() ${ \tilde {\bf r}}_{sm} \approx {\bf r}_{sm} $
,
${ \tilde {\bf r}}_{sm} \approx {\bf r}_{sm} $
,
![]() ${ \tilde {\bf r}}_{pi} \approx { \bar {\bf r}}_{pi} $
. The dynamic model of
${ \tilde {\bf r}}_{pi} \approx { \bar {\bf r}}_{pi} $
. The dynamic model of
![]() ${ \bar {\bf r}}_{sp} $
can be simplified as
${ \bar {\bf r}}_{sp} $
can be simplified as
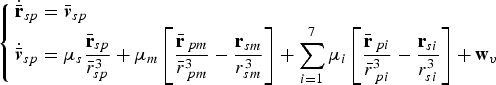 $$\left\{ {\matrix{ {{ \dot {\bar {\bf r}}}_{sp} = { \bar {\bi v}}_{sp}} \hfill \cr {{ \dot {\bar {\bi v}}}_{sp} = \mu _s \displaystyle{{{ \bar {\bf r}}_{sp}} \over {\bar r_{sp}^3}} + \mu _m \left[ {\displaystyle{{{ \bar {\bf r}}_{\,pm}} \over {\bar r_{\,pm}^3}} - \displaystyle{{{\bf r}_{sm}} \over {r_{sm}^3}}} \right] + \sum\limits_{i = 1}^7 {\mu _i \left[ {\displaystyle{{{ \bar {\bf r}}_{\,pi}} \over {\bar r_{\,pi}^3}} - \displaystyle{{{\bf r}_{si}} \over {r_{si}^3}}} \right] + {\bf w}_v}} \hfill \cr}} \right.$$
$$\left\{ {\matrix{ {{ \dot {\bar {\bf r}}}_{sp} = { \bar {\bi v}}_{sp}} \hfill \cr {{ \dot {\bar {\bi v}}}_{sp} = \mu _s \displaystyle{{{ \bar {\bf r}}_{sp}} \over {\bar r_{sp}^3}} + \mu _m \left[ {\displaystyle{{{ \bar {\bf r}}_{\,pm}} \over {\bar r_{\,pm}^3}} - \displaystyle{{{\bf r}_{sm}} \over {r_{sm}^3}}} \right] + \sum\limits_{i = 1}^7 {\mu _i \left[ {\displaystyle{{{ \bar {\bf r}}_{\,pi}} \over {\bar r_{\,pi}^3}} - \displaystyle{{{\bf r}_{si}} \over {r_{si}^3}}} \right] + {\bf w}_v}} \hfill \cr}} \right.$$
Positions of Deimos and Phobos obtained from Spacecraft Planet Instrument C_Matrix and Event (SPICE) (Arvidson et al., Reference Arvidson, Acton, Blaney, Bowman, Kim, Klingelhöfer, Marshall, Niebur, Plescia and Saunders1998) ephemeris are based on the position of Mars. Thus,
![]() ${ \tilde {\bf r}}_{pd} $
and
${ \tilde {\bf r}}_{pd} $
and
![]() ${ \tilde {\bf r}}_{pp} $
have the same position error
${ \tilde {\bf r}}_{pp} $
have the same position error
![]() $\Delta {\bf r}_{sm} $
as
$\Delta {\bf r}_{sm} $
as
![]() ${ \tilde {\bf r}}_{sm} $
, ignoring the error of SPICE. In other words,
${ \tilde {\bf r}}_{sm} $
, ignoring the error of SPICE. In other words,
![]() ${ \tilde {\bf r}}_{sd} = {\bf r}_{sd} + \Delta {\bf r}_{sm} $
,
${ \tilde {\bf r}}_{sd} = {\bf r}_{sd} + \Delta {\bf r}_{sm} $
,
![]() ${ \tilde {\bf r}}_{sph} = {\bf r}_{sph} + \Delta {\bf r}_{sm} $
. Because
${ \tilde {\bf r}}_{sph} = {\bf r}_{sph} + \Delta {\bf r}_{sm} $
. Because
![]() ${ \tilde {\bf r}}_{sp} = {\bf r}_{sp} + \Delta {\bf r}_{sm} $
, we have
${ \tilde {\bf r}}_{sp} = {\bf r}_{sp} + \Delta {\bf r}_{sm} $
, we have
![]() ${ \tilde {\bf r}}_{pd} = { \tilde {\bf r}}_{sd} - { \tilde {\bf r}}_{sp} = {\bf r}_{sd} - { \bar {\bf r}}_{sp} = { \bar {\bf r}}_{pd} $
and
${ \tilde {\bf r}}_{pd} = { \tilde {\bf r}}_{sd} - { \tilde {\bf r}}_{sp} = {\bf r}_{sd} - { \bar {\bf r}}_{sp} = { \bar {\bf r}}_{pd} $
and
![]() ${ \tilde {\bf r}}_{pp} = { \tilde {\bf r}}_{sph} - { \tilde {\bf r}}_{sp} = {\bf r}_{sph} - { \bar {\bf r}}_{sp} = { \bar {\bf r}}_{pp} $
. Thus the measurement model is shown as follows.
${ \tilde {\bf r}}_{pp} = { \tilde {\bf r}}_{sph} - { \tilde {\bf r}}_{sp} = {\bf r}_{sph} - { \bar {\bf r}}_{sp} = { \bar {\bf r}}_{pp} $
. Thus the measurement model is shown as follows.
 $${\bi Z} = \left[ {\matrix{ {\theta _m} \cr {\theta _p} \cr {\theta _d} \cr}} \right] = \left[ {\matrix{ {\arccos \left( {\displaystyle{{{ \tilde {\bf r}}_{\,pm} \bullet {\bf s}_1} \over {{\tilde r}_{\,pm}}}} \right)} \cr {\arccos \left( {\displaystyle{{{ \tilde {\bf r}}_{\,pp} \bullet {\bf s}_2} \over {{ \tilde {\bf r}}_{\,pp}}}} \right)} \cr {\arccos \left( {\displaystyle{{{ \tilde {\bf r}}_{\,pd} \bullet {\bf s}_3} \over {{\tilde r}_{\,pd}}}} \right)} \cr}} \right] + \left[ {\matrix{ {v_{\theta _m}} \cr {v_{\theta _p}} \cr {v_{\theta _d}} \cr}} \right] = \left[ {\matrix{ {\arccos \left( {\displaystyle{{{ \bar {\bf r}}_{\,pm} \bullet {\bf s}_1} \over {\bar r_{\,pm}}}} \right)} \cr {\arccos \left( {\displaystyle{{{ \bar {\bf r}}_{\,pp} \bullet {\bf s}_2} \over {\bar r_{\,pp}}}} \right)} \cr {\arccos \left( {\displaystyle{{{ \bar {\bf r}}_{\,pd} \bullet {\bf s}_3} \over {\bar r_{\,pd}}}} \right)} \cr}} \right] + \left[ {\matrix{ {v_{\theta _m}} \cr {v_{\theta _p}} \cr {v_{\theta _d}} \cr}} \right]$$
$${\bi Z} = \left[ {\matrix{ {\theta _m} \cr {\theta _p} \cr {\theta _d} \cr}} \right] = \left[ {\matrix{ {\arccos \left( {\displaystyle{{{ \tilde {\bf r}}_{\,pm} \bullet {\bf s}_1} \over {{\tilde r}_{\,pm}}}} \right)} \cr {\arccos \left( {\displaystyle{{{ \tilde {\bf r}}_{\,pp} \bullet {\bf s}_2} \over {{ \tilde {\bf r}}_{\,pp}}}} \right)} \cr {\arccos \left( {\displaystyle{{{ \tilde {\bf r}}_{\,pd} \bullet {\bf s}_3} \over {{\tilde r}_{\,pd}}}} \right)} \cr}} \right] + \left[ {\matrix{ {v_{\theta _m}} \cr {v_{\theta _p}} \cr {v_{\theta _d}} \cr}} \right] = \left[ {\matrix{ {\arccos \left( {\displaystyle{{{ \bar {\bf r}}_{\,pm} \bullet {\bf s}_1} \over {\bar r_{\,pm}}}} \right)} \cr {\arccos \left( {\displaystyle{{{ \bar {\bf r}}_{\,pp} \bullet {\bf s}_2} \over {\bar r_{\,pp}}}} \right)} \cr {\arccos \left( {\displaystyle{{{ \bar {\bf r}}_{\,pd} \bullet {\bf s}_3} \over {\bar r_{\,pd}}}} \right)} \cr}} \right] + \left[ {\matrix{ {v_{\theta _m}} \cr {v_{\theta _p}} \cr {v_{\theta _d}} \cr}} \right]$$
As we can see from Equations (11) and (12), the state model and the measurement model of
![]() ${ \bar {\bf r}}_{sp} $
are the same as Equations (5) and (6). Furthermore, the measurement depends on the sensor and does not relate to the Mars ephemeris as shown in Figure 5. Consequently,
${ \bar {\bf r}}_{sp} $
are the same as Equations (5) and (6). Furthermore, the measurement depends on the sensor and does not relate to the Mars ephemeris as shown in Figure 5. Consequently,
![]() ${ \bar {\bf r}}_{sp} $
and
${ \bar {\bf r}}_{sp} $
and
![]() ${ \bar {\bf v}}_{sp} $
are roughly equal to the position estimation (
${ \bar {\bf v}}_{sp} $
are roughly equal to the position estimation (
![]() ${\bf r}_{sp} $
) and the velocity (
${\bf r}_{sp} $
) and the velocity (
![]() ${\bf v}_{sp} $
) estimation without the Mars ephemeris error. Since
${\bf v}_{sp} $
) estimation without the Mars ephemeris error. Since
![]() ${ \tilde {\bf r}}_{sp} = { \bar {\bf r}}_{sp} + \Delta {\bf r}_{sm} $
and
${ \tilde {\bf r}}_{sp} = { \bar {\bf r}}_{sp} + \Delta {\bf r}_{sm} $
and
![]() ${ \tilde {\bf v}}_{sp} = { \bar {\bf v}}_{sp} + \Delta { \dot {\bf r}}_{sm} $
, the probe's position error caused by
${ \tilde {\bf v}}_{sp} = { \bar {\bf v}}_{sp} + \Delta { \dot {\bf r}}_{sm} $
, the probe's position error caused by
![]() $\Delta {\bf r}_{sm} $
in the Sun-centred inertial frame is equal to the Mars ephemeris error
$\Delta {\bf r}_{sm} $
in the Sun-centred inertial frame is equal to the Mars ephemeris error
![]() $\Delta {\bf r}_{sm} $
itself. The velocity error caused by
$\Delta {\bf r}_{sm} $
itself. The velocity error caused by
![]() $\Delta {\bf r}_{sm} $
is
$\Delta {\bf r}_{sm} $
is
![]() $\Delta { \dot {\bf r}}_{sm} $
, which is a small value.
$\Delta { \dot {\bf r}}_{sm} $
, which is a small value.
4.2. Influence of the Mars Ephemeris Error on the CNS in the Mars-centred Inertial Frame
When there is a Mars ephemeris error
![]() $\Delta {\bf r}_{sm} $
in the Sun-centred inertial frame, as shown in Figure 7, the coordinate X′
m
Y′
m
Z′
m
is the navigation frame, and the coordinate X
m
Y
m
Z
m
is the real Mars-centred inertial frame. The offset vector between two coordinates is
$\Delta {\bf r}_{sm} $
in the Sun-centred inertial frame, as shown in Figure 7, the coordinate X′
m
Y′
m
Z′
m
is the navigation frame, and the coordinate X
m
Y
m
Z
m
is the real Mars-centred inertial frame. The offset vector between two coordinates is
![]() $\Delta {\bf r}_{sm} $
. In the navigation frame, the Sun's and planets’ positions in the navigation frame can be represented by
$\Delta {\bf r}_{sm} $
. In the navigation frame, the Sun's and planets’ positions in the navigation frame can be represented by
![]() ${ \tilde {\bf r}}_{ms} = {\bf r}_{ms} - \Delta {\bf r}_{sm} $
and
${ \tilde {\bf r}}_{ms} = {\bf r}_{ms} - \Delta {\bf r}_{sm} $
and
![]() ${ \tilde {\bf r}}_{ms} = {\bf r}_{mi} - \Delta {\bf r}_{sm} $
. Assuming the position estimation and the velocity estimation in the Mars-centred frame are
${ \tilde {\bf r}}_{ms} = {\bf r}_{mi} - \Delta {\bf r}_{sm} $
. Assuming the position estimation and the velocity estimation in the Mars-centred frame are
![]() ${ \tilde {\bf r}}_{mp} $
and
${ \tilde {\bf r}}_{mp} $
and
![]() ${ \tilde {\bf v}}_{mp} $
, when the error Mars ephemeris is used, the state model is shown as follows.
${ \tilde {\bf v}}_{mp} $
, when the error Mars ephemeris is used, the state model is shown as follows.
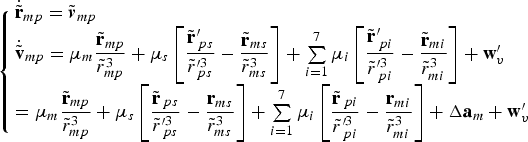 $$\left\{ {\matrix {{\dot {\tilde{ {\bf r}}}}_{mp} = {\tilde{\bi v}} _{mp} \hfill \cr { \dot {\tilde {\bf v}}}_{mp} = {\mu _m \displaystyle{{{{ \tilde {{\bf r}}}}_{mp}} \over {{\tilde r}_{mp}^3 }}} + {\mu _s} \left[{\displaystyle{{\tilde {{\bf r}}}_{\,ps}^{\prime} \over {\tilde {{r}}}_{\,ps}^{\prime 3}}} - {\displaystyle{{\tilde {{\bf r}}}_{ms} \over {\tilde {{r}}}_{ms}^{3}}}\right] + \sum\limits_{i = 1}^7 {\mu _i} \left[{\displaystyle{{\tilde {{\bf r}}}_{\,pi}^{\prime} \over {\tilde {{r}}}_{\,pi}^{\prime 3}}} - {\displaystyle{{\tilde {{\bf r}}}_{mi} \over {\tilde {{r}}}_{mi}^{3}}}\right] + {{\bf w}_{v}^{\prime}} \hfill \cr = {\mu _m \displaystyle{{{{ \tilde {{\bf r}}}}_{mp}} \over {{\tilde r}_{mp}^3 }}} + {\mu _s} \left[{\displaystyle{{\tilde {{\bf r}}}_{\,ps} \over {\tilde {{r}}}_{\,ps}^{\prime 3}}} - {\displaystyle{{ {{\bf r}}}_{ms} \over {\tilde {{r}}}_{ms}^{3}}}\right] + \sum\limits_{i = 1}^7 {\mu _i} \left[{\displaystyle{{\tilde {{\bf r}}}_{\,pi} \over {\tilde {{r}}}_{\,pi}^{\prime 3}}} - {\displaystyle{{ {{\bf r}}}_{mi} \over {\tilde {{r}}}_{mi}^{3}}}\right] + \Delta {\bf a}_m + {{\bf w}_{v}^{\prime}}}} \right.$$
$$\left\{ {\matrix {{\dot {\tilde{ {\bf r}}}}_{mp} = {\tilde{\bi v}} _{mp} \hfill \cr { \dot {\tilde {\bf v}}}_{mp} = {\mu _m \displaystyle{{{{ \tilde {{\bf r}}}}_{mp}} \over {{\tilde r}_{mp}^3 }}} + {\mu _s} \left[{\displaystyle{{\tilde {{\bf r}}}_{\,ps}^{\prime} \over {\tilde {{r}}}_{\,ps}^{\prime 3}}} - {\displaystyle{{\tilde {{\bf r}}}_{ms} \over {\tilde {{r}}}_{ms}^{3}}}\right] + \sum\limits_{i = 1}^7 {\mu _i} \left[{\displaystyle{{\tilde {{\bf r}}}_{\,pi}^{\prime} \over {\tilde {{r}}}_{\,pi}^{\prime 3}}} - {\displaystyle{{\tilde {{\bf r}}}_{mi} \over {\tilde {{r}}}_{mi}^{3}}}\right] + {{\bf w}_{v}^{\prime}} \hfill \cr = {\mu _m \displaystyle{{{{ \tilde {{\bf r}}}}_{mp}} \over {{\tilde r}_{mp}^3 }}} + {\mu _s} \left[{\displaystyle{{\tilde {{\bf r}}}_{\,ps} \over {\tilde {{r}}}_{\,ps}^{\prime 3}}} - {\displaystyle{{ {{\bf r}}}_{ms} \over {\tilde {{r}}}_{ms}^{3}}}\right] + \sum\limits_{i = 1}^7 {\mu _i} \left[{\displaystyle{{\tilde {{\bf r}}}_{\,pi} \over {\tilde {{r}}}_{\,pi}^{\prime 3}}} - {\displaystyle{{ {{\bf r}}}_{mi} \over {\tilde {{r}}}_{mi}^{3}}}\right] + \Delta {\bf a}_m + {{\bf w}_{v}^{\prime}}}} \right.$$
where
![]() ${ \tilde {\bf r}'}_{ps} = { \tilde {\bf r}}_{ms} - { \tilde {\bf r}}_{mp} $
is the estimated position of the probe relative to the Sun with the ephemeris error,
${ \tilde {\bf r}'}_{ps} = { \tilde {\bf r}}_{ms} - { \tilde {\bf r}}_{mp} $
is the estimated position of the probe relative to the Sun with the ephemeris error,
![]() ${ \tilde {\bf r}'}_{pi} = { \tilde {\bf r}}_{mi} - { \tilde {\bf r}}_{mp} $
is the estimated position of the probe relative to planet i with the ephemeris error,
${ \tilde {\bf r}'}_{pi} = { \tilde {\bf r}}_{mi} - { \tilde {\bf r}}_{mp} $
is the estimated position of the probe relative to planet i with the ephemeris error,
![]() ${ \tilde {\bf r}}_{ps} = {\bf r}_{ms} - { \tilde {\bf r}}_{mp} $
and
${ \tilde {\bf r}}_{ps} = {\bf r}_{ms} - { \tilde {\bf r}}_{mp} $
and
![]() ${ \tilde {\bf r}}_{pi} = {\bf r}_{mi} - { \tilde {\bf r}}_{mp} $
are the estimated position of the probe relative to the real position of the Sun and planet i.
${ \tilde {\bf r}}_{pi} = {\bf r}_{mi} - { \tilde {\bf r}}_{mp} $
are the estimated position of the probe relative to the real position of the Sun and planet i.
![]() $\Delta {\bf a}_m $
is the extra perturbation caused by Mars ephemeris error
$\Delta {\bf a}_m $
is the extra perturbation caused by Mars ephemeris error
![]() $\Delta {\bf r}_{sm} $
. The equation of
$\Delta {\bf r}_{sm} $
. The equation of
![]() $\Delta {\bf a}_m $
is shown as
$\Delta {\bf a}_m $
is shown as
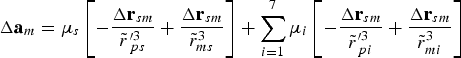 $$\Delta {\bf a}_m = \mu _s \left[ { - \displaystyle{{\Delta {\bf r}_{sm}} \over {{\tilde r}_{\,ps}^{\prime 3}}} + \displaystyle{{\Delta {\bf r}_{sm}} \over {{\tilde r}_{ms}^3}}} \right] + \sum\limits_{i = 1}^7 {\mu _i} \left[ { - \displaystyle{{\Delta {\bf r}_{sm}} \over {{\tilde r}_{\,pi}^{\prime 3}}} + \displaystyle{{\Delta {\bf r}_{sm}} \over {{\tilde r}_{mi}^3}}} \right]$$
$$\Delta {\bf a}_m = \mu _s \left[ { - \displaystyle{{\Delta {\bf r}_{sm}} \over {{\tilde r}_{\,ps}^{\prime 3}}} + \displaystyle{{\Delta {\bf r}_{sm}} \over {{\tilde r}_{ms}^3}}} \right] + \sum\limits_{i = 1}^7 {\mu _i} \left[ { - \displaystyle{{\Delta {\bf r}_{sm}} \over {{\tilde r}_{\,pi}^{\prime 3}}} + \displaystyle{{\Delta {\bf r}_{sm}} \over {{\tilde r}_{mi}^3}}} \right]$$
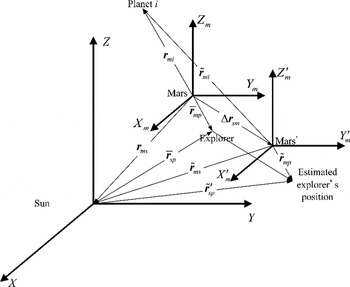
Figure 7. Positions of the Sun and planet i in the Mars-centred inertial frame.
Since
![]() $\Delta {\bf r}_{sm} \ll { \tilde {\bf r}}_{ps} $
,
$\Delta {\bf r}_{sm} \ll { \tilde {\bf r}}_{ps} $
,
![]() ${\bf r}_{mi} $
,
${\bf r}_{mi} $
,
![]() ${\bf r}_{ms} $
,
${\bf r}_{ms} $
,
![]() ${ \tilde {\bf r}}_{pi} $
,
${ \tilde {\bf r}}_{pi} $
,
![]() $\Delta {\bf a}_m $
can be ignored and
$\Delta {\bf a}_m $
can be ignored and
![]() ${ \tilde {\bf r}'}_{ps} \approx { \tilde {\bf r}}_{ps} $
,
${ \tilde {\bf r}'}_{ps} \approx { \tilde {\bf r}}_{ps} $
,
![]() ${ \tilde {\bf r}}_{mi} \approx {\bf r}_{mi} $
,
${ \tilde {\bf r}}_{mi} \approx {\bf r}_{mi} $
,
![]() ${ \tilde {\bf r}}_{ms} \approx {\bf r}_{ms} $
,
${ \tilde {\bf r}}_{ms} \approx {\bf r}_{ms} $
,
![]() ${ \tilde {\bf r}'}_{pi} \approx { \tilde {\bf r}}_{pi} $
. The state model can be presented as
${ \tilde {\bf r}'}_{pi} \approx { \tilde {\bf r}}_{pi} $
. The state model can be presented as
 $$\left\{ {\matrix{ {{ \dot {\tilde {\bf r}}}_{mp} = { \tilde {\bi v}}_{mp}} \hfill \cr {{ \dot {\tilde {\bf v}}}_{mp} = \mu _m \displaystyle{{{ \tilde {\bf r}}_{mp}} \over {{\tilde r}_{mp}^3}} + \mu _s \left[ {\displaystyle{{{ \tilde {\bf r}}_{\,ps}} \over {{\tilde r}_{\,ps}^3}} - \displaystyle{{{\bf r}_{ms}} \over {r_{ms}^3}}} \right] + \sum\limits_{i = 1}^7 {\mu _i \left[ {\displaystyle{{{ \tilde {\bf r}}_{\,pi}} \over {{\tilde r}_{\,pi}^3}} - \displaystyle{{{\bf r}_{mi}} \over {r_{mi}^3}}} \right] + {\bf w^{\prime}}_v}} \hfill \cr}} \right.$$
$$\left\{ {\matrix{ {{ \dot {\tilde {\bf r}}}_{mp} = { \tilde {\bi v}}_{mp}} \hfill \cr {{ \dot {\tilde {\bf v}}}_{mp} = \mu _m \displaystyle{{{ \tilde {\bf r}}_{mp}} \over {{\tilde r}_{mp}^3}} + \mu _s \left[ {\displaystyle{{{ \tilde {\bf r}}_{\,ps}} \over {{\tilde r}_{\,ps}^3}} - \displaystyle{{{\bf r}_{ms}} \over {r_{ms}^3}}} \right] + \sum\limits_{i = 1}^7 {\mu _i \left[ {\displaystyle{{{ \tilde {\bf r}}_{\,pi}} \over {{\tilde r}_{\,pi}^3}} - \displaystyle{{{\bf r}_{mi}} \over {r_{mi}^3}}} \right] + {\bf w^{\prime}}_v}} \hfill \cr}} \right.$$
The dynamic model shown in Equation (15) and the one shown in Equation (7) are identical. Thus the dynamic model in the Mars-centred inertial frame is hardly affected by the Mars ephemeris error. For the measurement model, Deimos and Phobos have the same ephemeris error as Mars. Thus, the measurement model in the Mars-centred inertial frame is untouched by the ephemeris error of Mars. As a result, when the Mars ephemeris with error is used, estimations of the probe's position and velocity relative to Mars (
![]() ${ \tilde {\bf r}}_{mp} $
and
${ \tilde {\bf r}}_{mp} $
and
![]() ${ \tilde {\bf v}}_{mp} $
) are equal to those without the Mars ephemeris error (
${ \tilde {\bf v}}_{mp} $
) are equal to those without the Mars ephemeris error (
![]() ${ \bar {\bf r}}_{mp} $
and
${ \bar {\bf r}}_{mp} $
and
![]() ${ \bar {\bf v}}_{mp} $
). The position estimation of the probe relative to the Sun is
${ \bar {\bf v}}_{mp} $
). The position estimation of the probe relative to the Sun is
![]() ${ \tilde {\bf r}'}_{sp} = { \tilde {\bf r}}_{mp} - { \tilde {\bf r}}_{ms} = { \bar {\bf r}}_{sp} + \Delta {\bf r}_{sm} $
. Thus, the position estimation of the probe relative to the Sun has an error equal to the Mars ephemeris error.
${ \tilde {\bf r}'}_{sp} = { \tilde {\bf r}}_{mp} - { \tilde {\bf r}}_{ms} = { \bar {\bf r}}_{sp} + \Delta {\bf r}_{sm} $
. Thus, the position estimation of the probe relative to the Sun has an error equal to the Mars ephemeris error.
As mentioned above, no matter in which frame, the position estimation of the probe relative to the Sun has an error equal to the Mars ephemeris error. The position estimation of the probe relative to Mars is unaffected by the Mars ephemeris error. The velocity estimation of the probe is independent of the Mars ephemeris error.
5. SIMULATIONS AND RESULTS
5.1. Simulation Condition
In the simulation, orbits of two Mars probes during an approach phase are used. The first is the orbit of the Mars Pathfinder, and the other orbit is an orbit in 2018. Their initial parameters are shown in Table 3. The ideal trajectories of the two Mars probes are obtained from the System Tool Kit (STK).
Table 3. Initial Parameters of the Mars Probes.

The ideal orbits of Mars, Deimos and Phobos are also obtained from STK using the DE421 and SPICE ephemeris, and Figure 8 shows these orbits in the Mars-centred inertial frame. The orbits of Mars, Phobos and Deimos with ephemeris errors are obtained by adding the ephemeris errors shown in Figures 1 and 2 to ideal orbits. As we can see from this figure, the approach directions of the two orbits are different. The orbit of the Mars Pathfinder is nearly in the ecliptic plane. The probe approaches from the vertical direction in 2018. The ideal measurements were created by a celestial navigation simulation platform using the ideal trajectory, Tycho-2 catalogue, JPL DE421 and SPICE. The field of view of sensor is 10°, and the pixel number of CCD is 1024 × 1024. The accuracy of the sensor is set as 0·3″.
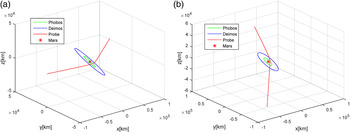
Figure 8. Ideal Orbits of Phobos, Deimos and the Probe. (a) Orbits in 1997 (b) Orbits in 2018.
The initial state
![]() ${\bf X}_0 $
has an error of
${\bf X}_0 $
has an error of
![]() $D{\bf X}_0 = \left[ {\matrix{ {1000m} \hfill & {1000m} \hfill & {1000m} \hfill & {0 \!\cdot \!1m/s} \hfill {0 \!\cdot\! 1m/s} \hfill & \;{0 \!\cdot\! 1m/s} \hfill \cr}}\right]$
. The initial state noise covariance matrix is set as
$D{\bf X}_0 = \left[ {\matrix{ {1000m} \hfill & {1000m} \hfill & {1000m} \hfill & {0 \!\cdot \!1m/s} \hfill {0 \!\cdot\! 1m/s} \hfill & \;{0 \!\cdot\! 1m/s} \hfill \cr}}\right]$
. The initial state noise covariance matrix is set as
![]() ${\bf P}_0 = {\rm diag}(10^6, 10^6, 10^6, 0 \!\cdot\! 01,0 \!\cdot\! 01,0 \!\cdot\! 01)$
. The initial process covariance matrix is set as
${\bf P}_0 = {\rm diag}(10^6, 10^6, 10^6, 0 \!\cdot\! 01,0 \!\cdot\! 01,0 \!\cdot\! 01)$
. The initial process covariance matrix is set as
![]() ${\bf Q}_0 = {\rm diag}(1,1,1,0 \!\cdot\! 0005,0 \!\cdot\! 0005,0 \!\cdot\! 0005)$
.
${\bf Q}_0 = {\rm diag}(1,1,1,0 \!\cdot\! 0005,0 \!\cdot\! 0005,0 \!\cdot\! 0005)$
.
5.2. Results and Analysis
5.2.1. Influence of Mars ephemeris errors
In this section, we use the position and velocity errors of the probe as the evaluation of the navigation. The errors are obtained by the differences between the estimated orbit and the ideal one. The orbit of the Mars Pathfinder is used for analysis. To evaluate the influence of Mars ephemeris error, this paper analyses the navigation results of CNS with different Mars ephemeris errors. The normal setting of Mars ephemeris error is shown as Figure 1, where the position error is
![]() $\Delta r_m = \sqrt {\Delta x_m^2 + \Delta y_m^2 + \Delta z_m^2} \approx 340m$
. Navigation errors of the probe without Mars ephemeris error in x, y, z directions are expressed as Δx
0, Δy
0, Δz
0. When the Mars ephemeris error is k times the normal setting (k = 1, 2, 3), the position and velocity errors of the probe in x, y, z directions are expressed as Δx
k
, Δy
k
, Δz
k
and Δv
xk
, Δv
yk
, Δv
zk
. We define position and velocity estimation errors of the probe as
$\Delta r_m = \sqrt {\Delta x_m^2 + \Delta y_m^2 + \Delta z_m^2} \approx 340m$
. Navigation errors of the probe without Mars ephemeris error in x, y, z directions are expressed as Δx
0, Δy
0, Δz
0. When the Mars ephemeris error is k times the normal setting (k = 1, 2, 3), the position and velocity errors of the probe in x, y, z directions are expressed as Δx
k
, Δy
k
, Δz
k
and Δv
xk
, Δv
yk
, Δv
zk
. We define position and velocity estimation errors of the probe as
![]() $\Delta r_k = \sqrt {\Delta x_k^2 + \Delta y_k^2 + \Delta z_k^2} $
and
$\Delta r_k = \sqrt {\Delta x_k^2 + \Delta y_k^2 + \Delta z_k^2} $
and
![]() $\Delta v_k = \sqrt {\Delta v_{xk}^2 + \Delta v_{yk}^2 + \Delta v_{zk}^2} $
.
$\Delta v_k = \sqrt {\Delta v_{xk}^2 + \Delta v_{yk}^2 + \Delta v_{zk}^2} $
.
5.2.1.1. In the Sun-centred inertial frame
Figure 9(a) shows the position errors of the probe in the x, y, z directions with the different ephemeris errors respectively. When there are different Mars ephemeris errors, the change-of-position errors are alike. To show this clearly, the differences between the estimation results with and without the ephemeris error (Δx
k
− Δx
0, Δy
k
− Δy
0 and Δz
k
− Δz
0) are shown in Figure 9(b). We can see that differences of the probe's position errors in the three directions approximately correspond to the constants after filter convergence. Δx
1 − Δx
0, Δy
1 − Δy
0 and Δz
1 − Δz
0 are equal to Δx
m
, Δy
m
and Δz
m
as shown in Figure 1. For the other cases,
![]() $\Delta x_k - \Delta x_0 \approx k(\Delta x_1 - \Delta x_0 )$
,
$\Delta x_k - \Delta x_0 \approx k(\Delta x_1 - \Delta x_0 )$
,
![]() $\Delta y_k - \Delta y_0 \approx k(\Delta y_1 - \Delta y_0 )$
and
$\Delta y_k - \Delta y_0 \approx k(\Delta y_1 - \Delta y_0 )$
and
![]() $\Delta z_k - \Delta z_0 \approx k(\Delta z_1 - \Delta z_0 )$
. This shows that in the Sun-centred inertial frame the position estimation of the probe relative to the Sun has an error that almost equals the Mars ephemeris error.
$\Delta z_k - \Delta z_0 \approx k(\Delta z_1 - \Delta z_0 )$
. This shows that in the Sun-centred inertial frame the position estimation of the probe relative to the Sun has an error that almost equals the Mars ephemeris error.
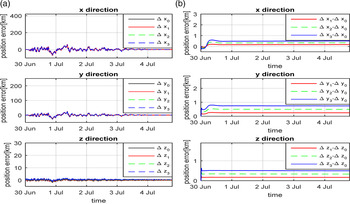
Figure 9. Position errors with different ephemeris errors of Mars in the Sun-centred frame. (a) Position error (b) Differences.
Figure 10 (a) shows the estimation errors of the probe's velocity with different Mars ephemeris errors. Figure 10 (b) shows the value of
![]() $\Delta {\bf v}_k - \Delta {\bf v}_0 $
. From Figure 10 we can see that the estimation errors of velocity with different Mars-ephemeris errors are similar, and the differences are small values. This demonstrates that in the Sun-centred inertial frame the velocity error caused by ephemeris errors of Mars is small, which is consistent with the theoretical analysis in Section 4.1.
$\Delta {\bf v}_k - \Delta {\bf v}_0 $
. From Figure 10 we can see that the estimation errors of velocity with different Mars-ephemeris errors are similar, and the differences are small values. This demonstrates that in the Sun-centred inertial frame the velocity error caused by ephemeris errors of Mars is small, which is consistent with the theoretical analysis in Section 4.1.

Figure 10. Velocity errors with different ephemeris errors of Mars in the Sun-centred frame. (a) Velocity error (b) Difference.
5.2.1.2. Influence in the Mars-centred Inertial Frame
Similarly, the navigation results in the Mars-centred inertial frame are also analysed in relation to different Mars ephemeris errors. The simulation conditions are the same as those in the Sun-centred inertial frame. The navigation results are shown in Figures 11 and 12.
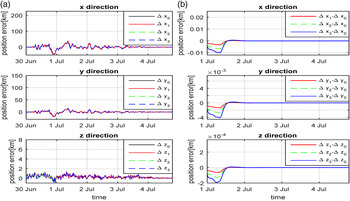
Figure 11. Position errors with different ephemeris errors of Mars in the Mars-centred frame. (a) Position error (b) Difference.

Figure 12. Velocity errors with different ephemeris errors of Mars in the Mars-centred frame. (a) Velocity error (b) Difference.
Figure 11 (a) shows the position error with different Mars ephemeris errors, and Figure 11 (b) shows the corresponding differences. Figure 12 (a) shows the velocity errors with different Mars ephemeris errors and Figure 12 (b) shows the corresponding differences. From Figures 11 and 12, we can see that in the Mars-centred inertial frame, the navigation results with different Mars ephemeris errors are similar, which demonstrates that the Mars ephemeris error hardly affects the navigation result in the Mars-centred inertial frame. The simulation results shown in this section are consistent with the theoretical analysis in section 4.2.
5.2.2. Influence of ephemeris errors of Phobos and Deimos in the Mars-centred inertial frame
Because the navigation performance in the Mars-centred inertial frame is better than that in the Sun-centred inertial frame, we only analysed the influence of the ephemeris errors of Phobos and Deimos in the Mars-centred inertial frame in this section. To evaluate the influence of ephemeris errors of Phobos and Deimos, ephemerides with different levels of errors are used in a CNS. The basic ephemeris errors are shown in Figure 2. The ephemerides with errors two and three times larger than basic errors are also used for analysing the influence of larger ephemeris errors.
5.2.2.1. Navigation result of the orbit of the Mars Pathfinder in 1997
Figure 13 (a) shows the navigation errors without ephemeris errors. Figure 13 (b) shows those with basic ephemeris errors, and Figure 13 (c) and (d) show navigation errors up to two and three times larger than basic ephemeris errors. As shown in Figure 13(b), the navigation is obviously affected by the ephemeris errors of Phobos and Deimos, where the ephemeris errors are about 1 km and 2 km respectively. The navigation errors are affected by the periodicity of the ephemeris errors. As shown in Figure 4, the position error of Deimos is about 1 km larger than that of Phobos, thus the navigation error of the probe is mainly affected by the periodicity of Deimos, whose period is about 30 hours. The influence of periodicity also appears when the ephemeris errors are two and three times larger than basic errors, and the values of navigation errors increase as the values of the ephemeris errors rise greatly.

Figure 13. Navigation errors of the orbit in 1997 with different ephemeris errors of Phobos and Deimos. (a) Without ephemeris errors (b) With basic ephemeris errors (c) With errors two times larger than basic errors (d) With errors three times larger than basic errors.
In addition, to clearly show the influences of different ephemeris errors, we count the data from 4 July 05:00:00·000 to 4 July 17:00:00·000, during which the probe approaches nearest to Mars, and the Root Mean Square (RMS) of the navigation errors are shown in Table 4. As we can see from the table, the influences on the navigation in three directions are different. When there are basic ephemeris errors, the navigation error in the x direction increases from 0·81 km to 4·52 km, while the navigation error in the z direction only increases from 0·09 km to 0·53 km.
Table 4. RMS of navigation errors of the orbit in 1997 with different ephemeris errors.

5.2.2.2. Navigation result using the orbit of the Mars probe in 2018
As shown in Figure 14, similar to the navigation result of the orbit in 1997, the navigation errors of the probe in 2018 are also affected by the quantity and periodicity of the ephemeris errors of Phobos and Deimos, and mainly affected by the periodicity of ephemeris error of Deimos. Similarly, we also count the RMS of navigation errors from 14 Jan 00:00:00·000 to 14 Jan 12:00:00·000 in the Mars-centred inertial frame, and the results are shown in Table 5. As we can see, the navigation error in the x direction is the smallest and is also the least affected by the ephemeris errors for the orbit in 2018. Considering the navigation results of the two orbits, we find that the influence of ephemeris errors on each direction depends on the orbit component in this direction. As we can see from Figure 8(a), for the orbit in 1997, the orbit component in the z direction is much smaller than those in the other two directions, and navigation in the z direction is least affected by the ephemeris errors. Similarly, from Figure 8(b), for the orbit in 2018, the orbit component in the x direction is the smallest. Thus the navigation error in the x direction is least affected. Meanwhile, we also find that the influences of ephemeris errors of Phobos and Deimos on different orbits are also different, and the navigation errors of the orbit in 2018 are easily affected by the ephemeris errors.
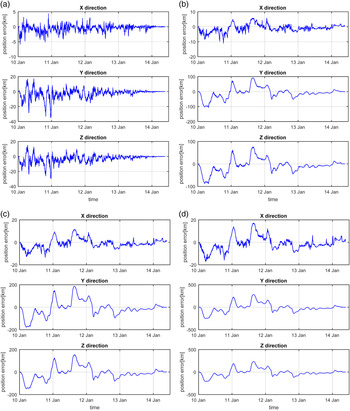
Figure 14. Navigation errors of the orbit in 2018 with different ephemeris errors of Phobos and Deimos. (a) Without ephemeris errors (b) With basic errors (c) With errors two times larger than basic errors (d) With errors three times larger than basic errors.
Table 5. Navigation Errors of the Orbit in 2018 with Different Ephemeris Errors.

5.3. Analysis
As we can see from the analysis in Section 4, the ephemeris error of Mars directly affects the navigation result in the Sun-centred inertial frame, and the navigation errors are equal to the ephemeris errors of Mars. In the Mars-centred inertial frame, the Mars ephemeris error does not affect the measurement model. However, the ephemeris error of Mars affects the positions of other planets in the Mars-centred inertial frame, which are used in the state model. Thus, the ephemeris error of Mars slightly affects the navigation result. The simulations in Section 5.2.1 demonstrate our theoretical analysis. The simulation also shows that the navigation accuracy in the Mars-centred inertial frame is better than that in the Sun-centred inertial frame. According to this, we only analyse the influence of the ephemeris errors of Phobos and Deimos in the Mars-centred inertial frame. Although the ephemeris errors of Phobos and Deimos only affect the measurement model of CNS, they have a great influence on the navigation result. During the approach phase, even 1 km position errors of Phobos and 2 km errors of Deimos can cause a great decrease in navigation accuracy, as shown in Tables 4 and 5. Moreover, the navigation result is also affected by the periodicity of the position errors of Phobos and Deimos, especially Deimos which has larger ephemeris errors. It also shows that due to the different orbit components in the three directions, the influences of ephemeris errors on navigation errors in the three directions are different.
Finally, we analyse whether CNS can reach the navigation requirement of the deep-space mission during the approach phase, and whether it is necessary to correct the ephemeris errors. According to the existing deep-space missions, a 10 km navigation error is acceptable during approach. As shown in Tables 4 and 5, when there is no ephemeris error, the accuracy of the CNS is better than 1 km, which is definitely sufficient for the approach phase. When the ephemeris errors of Phobos and Deimos are about 2 km and 1 km respectively, the CNS can reach an accuracy better than 10 km. When the ephemeris errors are about 4 km and 2 km respectively, the navigation error for the orbit in 1997 is less than 10 km, but the navigation error for the orbit in 2018 is about 16 km, which is much larger than the acceptable accuracy. Thus, the CNS with normal ephemeris errors can reach the requirement of the approach phase, but larger ephemeris errors could easily spoil the navigation accuracy.
6. CONCLUSIONS
In this paper, the ephemeris errors of Mars, Phobos and Deimos are first analysed. The analysis shows that during the Mars approach phase, the ephemeris errors of Mars are slowly-varying, and ephemeris errors of Phobos and Deimos are periodical. The influence of the Mars ephemeris error on the CNS system models is analysed in both the Sun-centred inertial frame and the Mars-centred inertial frame by theoretical analysis and simulations. We find that in the Sun-centred inertial frame the navigation errors caused by ephemeris errors of Mars are equal to the ephemeris errors themselves, but the velocity errors are slightly affected. In the Mars-centred inertial frame, the ephemeris error of Mars hardly affects the navigation results. Then the influences of ephemeris errors of Phobos and Deimos are analysed by simulation using two different orbits. The simulation result shows that the navigation result of the Mars probe is greatly affected by the quantities and periodicities of ephemeris errors of Phobos and Deimos, especially those of Deimos. The different influence of ephemeris errors on each direction mainly depends on the orbit component in this direction. Compared with the navigation method used in the existing deep-space missions, when there are normal ephemeris errors of Phobos and Deimos, CNS can achieve a fine navigation result. However, larger ephemeris errors of Phobos and Deimos could easily spoil the navigation. Thus it is necessary to work on reducing the influence of the ephemeris errors of Phobos and Deimos, and new methods for correcting ephemeris errors online require further research.
ACKNOWLEDGMENTS
The research presented in this paper has been supported by the National Natural Science Foundation of China (61233005, 61503013), Beijing Youth Talent Program, the grant of National Basic Research Program of China (973 Program 2014CB744206). The authors wish to express their gratitude to all members of the Science & Technology on Inertial Laboratory, Fundamental Science on Novel Inertial Instrument & Navigation System Technology Laboratory and Innovative Research Team in University (IRT1203) for their valuable comments.























