Hostname: page-component-76fb5796d-9pm4c Total loading time: 0 Render date: 2024-04-26T22:14:45.924Z Has data issue: false hasContentIssue false
  • English
  • Français

On the numerical modeling of nucleation and growth of microstructurally short cracks in polycrystals under cyclic loading

Published online by Cambridge University Press:  17 September 2019

Martin Boeff ,
Hamad ul Hassan Open the ORCID record for Hamad ul Hassan [Opens in a new window]  and
Alexander Hartmaier Open the ORCID record for Alexander Hartmaier [Opens in a new window]
Martin Boeff
Affiliation:
Interdisciplinary Centre for Advanced Materials Simulation, Ruhr-Universität Bochum, Bochum 44801, Germany
Hamad ul Hassan*
Affiliation:
Interdisciplinary Centre for Advanced Materials Simulation, Ruhr-Universität Bochum, Bochum 44801, Germany
Alexander Hartmaier
Affiliation:
Interdisciplinary Centre for Advanced Materials Simulation, Ruhr-Universität Bochum, Bochum 44801, Germany
*
a)Address all correspondence to this author. e-mail: Hamad.ulhassan@rub.de
Get access

Abstract

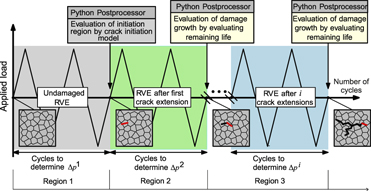
In the scope of this work, a micromechanical model based on the crystal plasticity finite element method is proposed and applied to describe the nucleation and growth of microstructurally short fatigue cracks in polycrystalline materials under cyclic loads. The microstructure is generated in the form of a representative volume element of a polycrystalline material with equiaxed grains having columnar structure along thickness and random crystallographic texture. With this model, we investigate the influence of loading amplitude on the crack growth behavior. It is shown that for smaller strain amplitudes, a single crack nucleates and propagates, while for larger strain amplitudes several independent crack nucleation sites form, from which microcracks start propagating. It is also observed that the global plastic strain amplitude decreases from the initial to the final cycle, during total strain-controlled loading. However, this can even increase the crack growth rate because the crack advance is governed by the local plastic slip which accumulates at the crack tip over the number of cycles. With this work, it is shown that micromechanical modeling can strongly improve our understanding of the mechanisms of short-crack nucleation and growth under fatigue loading.

Keywords

fatiguesimulationmicrostructure
Type
Article
Information
Journal of Materials Research , Volume 34 , Issue 20 , 28 October 2019 , pp. 3523 - 3534
Copyright
Copyright © Materials Research Society 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Christ, H.J., Fritzen, C.P., and Köster, P.: Micromechanical modeling of short fatigue cracks. Curr. Opin. Solid State Mater. Sci. 18, 205 (2014).CrossRefGoogle Scholar
Mughrabi, H.: Microstructural fatigue mechanisms: Cyclic slip irreversibility, crack initiation, non-linear elastic damage analysis. Int. J. Fatigue 57, 2 (2013).CrossRefGoogle Scholar
Aslan, O., Quilici, S., and Forest, S.: Numerical modeling of fatigue crack growth in single crystals based on microdamage theory. Int. J. Damage Mech. 20, 681 (2011).CrossRefGoogle Scholar
Mughrabi, H.: On the life-controlling microstructural fatigue mechanisms in ductile metals and alloys in the gigacycle regime. Fatigue Fract. Eng. Mater. Struct. 22, 633 (1999).CrossRefGoogle Scholar
Mughrabi, H.: On “multi-stage” fatigue life diagrams and the relevant life-controlling mechanisms in ultrahigh-cycle fatigue. Fatigue Fract. Eng. Mater. Struct. 25, 755 (2002).CrossRefGoogle Scholar
Tokaji, K. and Ogawa, T.: The growth behaviour of microstructurally small fatigue cracks in metals. Mech. Eng. Publ. 13, 85 (1992).Google Scholar
Suresh, S.: Fatigue of Materials (Cambridge University Press, Cambridge, U.K., 1998).CrossRefGoogle Scholar
Bennett, V. and McDowell, D.L.: Mixed-Mode Crack Behavior (ASTM International, West Conshohocken, Pennsylvania, 1999); pp. 203–228.CrossRefGoogle Scholar
Simonovski, I., Nilsson, K.F., and Cizelj, L.: The influence of crystallographic orientation on crack tip displacements of microstructurally small, kinked crack crossing the grain boundary. Comput. Mater. Sci. 39, 817 (2007).CrossRefGoogle Scholar
Krupp, U., Düber, O., Christ, H.J., Künkler, B., Schick, A., and Fritzen, C.P.: Application of the EBSD technique to describe the initiation and growth behaviour of microstructurally short fatigue cracks in a duplex steel. J. Microsc. 213, 313 (2004).CrossRefGoogle Scholar
Przybyla, C.P. and McDowell, D.L.: Microstructure-sensitive extreme value probabilities for high cycle fatigue of Ni-base superalloy IN100. Int. J. Plast. 26, 372 (2010).CrossRefGoogle Scholar
McDowell, D.L. and Dunne, F.P.E.: Microstructure-sensitive computational modeling of fatigue crack formation. Int. J. Fatigue 32, 1521 (2010).CrossRefGoogle Scholar
Li, Y., Aubin, V., Rey, C., and Bompard, P.: Microstructural modeling of fatigue crack initiation in austenitic steel 304L. Procedia Eng. 31, 541 (2012).CrossRefGoogle Scholar
Marchal, N., Forest, S., Rémy, L., and Duvinage, S.: Fatigue and creep. Local Approach to Fracture EUROMECH-MECAMAT 2006, 9th European Mechanics of Materials Conference, Besson, D.S.J. and Moinereau, D., ed. (Presses des Mines de Paris, Moret Sur Loing, France, 2006); pp. 353–358.Google Scholar
Zhao, L.G., O’Dowd, N.P., and Busso, E.P.: A coupled kinetic-constitutive approach to the study of high temperature crack initiation in single crystal nickel-base superalloys. J. Mech. Phys. Solids 54, 288 (2006).CrossRefGoogle Scholar
Zhao, L.G., Tong, J., and Byrne, J.: The evolution of the stress–strain fields near a fatigue crack tip and plasticity-induced crack closure revisited. Fatigue Fract. Eng. Mater. Struct. 27, 19 (2004).CrossRefGoogle Scholar
Tong, J., Lin, B., Lu, Y.W., Madi, K., Tai, Y.H., Yates, J.R., and Doquet, V.: Near-tip strain evolution under cyclic loading: In situ experimental observation and numerical modelling. Int. J. Fatigue 71, 45 (2015).CrossRefGoogle Scholar
Carroll, J.D., Abuzaid, W., Lambros, J., and Sehitoglu, H.: High resolution digital image correlation measurements of strain accumulation in fatigue crack growth. Int. J. Fatigue 57, 140 (2013).CrossRefGoogle Scholar
Miller, K.J.: The short crack problem. Fatigue Fract. Eng. Mater. Struct. 5, 223 (1982).CrossRefGoogle Scholar
Tokaji, K., Ogawa, T., Harada, Y., and Ando, Z.: Limitations of linear elastic fracture mechanics in respect of small fatigue cracks and microstructure. Fatigue Fract. Eng. Mater. Struct. 9, 1 (1986).CrossRefGoogle Scholar
Rice, J.R.: Tensile crack tip fields in elastic-ideally plastic crystals. Mech. Mater. 6, 317 (1987).CrossRefGoogle Scholar
Gall, K., Sehitoglu, H., and Kadioglu, Y.: FEM study of fatigue crack closure under double slip. Acta Mater. 44, 3955 (1996).CrossRefGoogle Scholar
Leverant, G.R. and Gell, M.: The influence of temperature and cyclic frequency on the fatigue fracture of cube oriented nickel-base superalloy single crystals. Metall. Trans. A 6, 367 (1975).CrossRefGoogle Scholar
Crompton, J.S. and Martin, J.W.: Crack tip plasticity and crack growth in a single-crystal superalloy at elevated temperatures. Mater. Sci. Eng. 64, 37 (1984).CrossRefGoogle Scholar
Aswath, P.B.: Effect of orientation on crystallographic cracking in notched nickel-base superalloy single crystal subjected to far-field cyclic compression. Metall. Mater. Trans. A 25, 287 (1994).CrossRefGoogle Scholar
Gurson, A.L.: Continuum theory of ductile rupture by void nucleation and growth: Part I—Yield criteria and flow rules for porous ductile media. J. Eng. Mater. Technol. 99, 2 (1977).CrossRefGoogle Scholar
Tvergaard, V. and Needleman, A.: Analysis of the cup-cone fracture in a round tensile bar. Acta Metall. 32, 157 (1984).CrossRefGoogle Scholar
Mahnken, R.: Theoretical, numerical and identification aspects of a new model class for ductile damage. Int. J. Plast. 18, 801 (2002).CrossRefGoogle Scholar
Lillbacka, R., Johnson, E., and Ekh, M.: A model for short crack propagation in polycrystalline materials. Eng. Fract. Mech. 73, 223 (2006).CrossRefGoogle Scholar
Künkler, B., Fritzen, C-P., Düber, O., Krupp, U., and Christ, H-J.: Simulation of short crack propagation—Transition from stage I to stage II. Proc. Appl. Math. Mech. 5, 341 (2005).CrossRefGoogle Scholar
Düber, O., Künkler, B., Krupp, U., Christ, H.J., and Fritzen, C.P.: Experimental characterization and two-dimensional simulation of short-crack propagation in an austenitic-ferritic duplex steel. Int. J. Fatigue 28, 983 (2006).CrossRefGoogle Scholar
Castelluccio, G.M.: A Study on the Influence of Microstructure on Small Fatigue Cracks (Georigia Institute of Technology, 2012).Google Scholar
Bouvard, J.L., Chaboche, J.L., Feyel, F., and Gallerneau, F.: A cohesive zone model for fatigue and creep–fatigue crack growth in single crystal superalloys. Int. J. Fatigue 31, 868 (2009).CrossRefGoogle Scholar
Boeff, M.: Micromechanical modelling of fatigue crack initiation and growth. Ph.D. thesis, Ruhr Universität Bochum, Germany, 2016.Google Scholar
Boeff, M., Hassan, H.U., and Hartmaier, A.: Micromechanical modeling of fatigue crack initiation in polycrystals. J. Mater. Res. 32, 4375 (2017).CrossRefGoogle Scholar
Cubit 13.2 by (Sandia National Laboratories, Albuquerque, New Mexico, 2013).Google Scholar
Rice, J.R.: Inelastic constitutive relations for solids: Theory and its application to metal plasticity. J. Mech. Phys. Solids 19, 433 (1971).CrossRefGoogle Scholar
Hutchinson, J.W.: Bounds and self-consistent estimates for creep of polycrystalline materials. Proc. R. Soc. A 348, 101 (1976).CrossRefGoogle Scholar
Roters, F., Eisenlohr, P., Hantcherli, L., Tjahjanto, D.D., Bieler, T.R., and Raabe, D.: Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications. Acta Mater. 58, 1152 (2010).CrossRefGoogle Scholar
Inal, K., Lebrun, J.L., and Belassel, M.: Second-order stresses and strains in heterogeneous steels: Self-consistent modeling and X-ray diffraction analysis. Metall. Mater. Trans. A 35, 2361 (2004).CrossRefGoogle Scholar
Mahmoody, S.: Micromechanical Modeling of Dual-Phase Steel Using a Rate-Dependent Crystal Plasticity Model (McGill University, Montreal, Canada, 2003).Google Scholar
McDowell, D.L.: Simulation-based strategies for microstructure-sensitive fatigue modeling. Mater. Sci. Eng., A 468–470(Spec. Iss.), 4 (2007).CrossRefGoogle Scholar
Manonukul, A. and Dunne, F.P.E.: High- and low-cycle fatigue crack initiation using polycrystal plasticity. Proc. R. Soc. London, Ser. A 460, 1881 (2004).CrossRefGoogle Scholar
Pijaudier-Cabot, G. and Bazant, Z.: Nonlocal damage theory. J. Eng. Mech. 113, 1512–1533 (1987).CrossRefGoogle Scholar
Peerlings, R.H.J.: Enhanced Damage Modelling for Fracture and Fatigue (Technische Universiteit Eindhoven, Eindhoven, Netherlands, 1999).Google Scholar
Polák, J., Kruml, T., Obrtlík, K., Man, J., and Petrenec, M.: Short crack growth in polycrystalline materials. Procedia Eng. 2, 883 (2010).CrossRefGoogle Scholar
Schlesinger, M.: Experimentelle Untersuchung Des Zeitabhängigen Rissfortschritts Unter Thermomechanischer Ermüdung in Nickellegierungen Und Mechanismenbasierte Modelle Zur Lebensdauerbewertung (Shaker Verlag, Aachen, 2014).Google Scholar