Article contents
Intrinsic point defects in ternary MgCaSi: Ab initio investigation
Published online by Cambridge University Press: 01 August 2017
Abstract
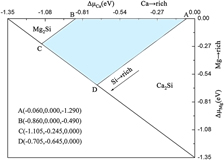
Nine possible native point defects in MgCaSi have been studied by employing density functional theory based ab initio calculations. The complex chemical potential limits are first determined using a two-dimension (∆μMg, ∆μCa) diagram, then the defect formation energies as a function of the atomic chemical potential are gained. The energetic results show that under Mg-rich conditions, the most favorable defect is MgCa rather than MgSi, while CaMg is predominant compared to CaSi under Ca-rich conditions. The bonding energy is first introduced to uncover the intrinsic feature of defect formation energy. The local geometric distortion around CaMg, MgSi, and CaSi antisite defects gradually increases due to the smaller atomic radii from Ca to Mg and Si, showing the important role of the geometrical mismatch. The density of states indicates that the higher stability of CaMg and MgCa originates from the smaller deviation of the Fermi level from the pseudo-gap.
Keywords
- Type
- Articles
- Information
- Copyright
- Copyright © Materials Research Society 2017
Footnotes
Contributing Editor: Susan B. Sinnott
References
REFERENCES
- 3
- Cited by





