1. Introduction
Many glaciers on Svalbard and the eastern side of the Scandinavian mountains are polythermal, with a perennial cold surface layer overlying a temperate core in the ablation area (e.g. Reference SchyttSchytt, 1968; Reference BaranowskiBaranowski, 1977; Björnsson and others, 1996; Reference Pettersson, Jansson and HolmlundPettersson and others, 2003), while the accumulation areas are completely temperate (Reference Holmlund and ErikssonHolmlund and Eriksson, 1989; Reference Ødegard, Hamran, Bø, Etzelmuller, Vatne and SollidØdegård and others, 1992). The general cause of the polythermal structure is known, but the details of the processes involved are poorly understood. This has become evident from studies of the thinning of the cold surface layer on Storglaciären, northern Sweden (Reference Pettersson, Jansson and HolmlundPettersson and others, 2003).
The polythermal structure is a result of energy balance at the glacier surface. During winter a strong net loss of energy at the glacier surface causes the glacier ice to cool. In spring, when surface melting starts, the accumulation area quickly turns temperate due to the release of latent heat through freezing of percolating meltwater. In the ablation area, the surface warms to the melting point by the release of latent heat, but the impermeable ice surface prevents any percolation of meltwater. Any heating of the ice below the surface must occur through heat conduction from the surface. This is a slow process, as ice is a poor conductor and the amount of heat is limited since the ice surface temperature cannot rise above the melting point. The result is that the ice below the surface remains cold throughout the year.
The thickness of the cold surface layer is a function of the surface energy flux, net ablation at the glacier surface and liquid-water content of the ice entering the cold surface layer, as well as the velocity field (Reference Hutter, Blatter and FunkHutter and others, 1988; Reference Blatter and HutterBlatter and Hutter, 1991; Reference Pettersson, Jansson and HolmlundPettersson and others, 2003). The negative temperature gradient through the cold surface layer causes the base of the cold layer to migrate downwards by freezing of temperate ice. The rate of this migration is determined by the amount of latent heat released when the temperate ice freezes, and the abillity to transport away the released heat from the cold–temperate transition surface (CTS), which is governed by the temperature gradient in the cold surface ice. In turn, the amount of latent heat released depends on the volume of liquid water in the temperate ice that needs to freeze when the freezing front migrates. The balance between the value of downward migration of the CTS and the removal of ice at the surface by melting over a longer period of time determines the thickness of the cold surface layer.
Both the ice surface temperature and the net ablation at the glacier surface are directly linked to the prevailing local climate, while the ice flow is indirectly related to local climate conditions by its dependence on mass balance. This suggests that forcing of the cold surface layer thickness is probably not stable in time as the climate varies. Repeated ground-penetrating radar surveys of the cold surface layer on Storglaciären indicate an average thinning of ~20°% of the cold surface layer over a 12 year period (Reference Pettersson, Jansson and HolmlundPettersson and others, 2003). However, the thinning is not uniform and areas with insignificant thinning indicate complex interactions between the forcing factors of the cold surface layer thickness, implying that the processes are not fully understood.
We use a one-dimensional time-dependent heat diffusion and advection model to evaluate the dynamics of the cold surface layer and the sensitivity of the cold surface layer thickness to different forcing parameters on Storglaciären. For the model we use measured values of ice surface temperature, emergence velocity, mass balance and water content of the temperate ice as the forcing parameters. In addition, we investigate their spatial distribution. The aim is to provide better understanding of the causes of the spatial variability of the cold surface layer and the causes of the cold surface layer thinning observed on Storglaciären. The results show that the cold surface layer thickness is strongly influenced by variations in the emergence velocity and ablation shown by similarities between the general pattern in cold surface layer thickness and variations in vertical velocity and net ablation. The thinning of the cold surface layer is probably caused by an increased winter temperature that has occurred during recent decades, while the complex thinning pattern results from spatial variations in emergence velocity, as the cold surface layer would thin considerably more in areas with low emergence velocity than those with higher velocities.
2. Storglaciären
Storglaciären is a well-studied glacier in northern Sweden, which has a long documented record of mass balance, ice dynamics and hydrological studies (e.g. Reference Brzozowski and HookeBrzozowski and Hooke, 1981; Reference Hooke, Calla, Holmlund, Nilsson and StroevenHooke and others, 1989; Reference JanssonJansson, 1996; Reference Holmlund and JanssonHolmlund and Jansson, 1999). Detailed information on the overall glacier geometry is available from several topographic surface maps (Reference HolmlundHolmlund, 1996) and a bed topography map from radio-echo soundings and borehole drillings (Reference Herzfeld, Eriksson and HolmlundHerzfeld and others, 1993). The polythermal structure is known from several detailed ground-penetrating radar surveys of the cold surface layer (Reference Holmlund and ErikssonHolmlund and Eriksson, 1989; Reference Holmlund, Naslund and RichardsonHolmlund and others, 1996b; Reference Pettersson, Jansson and HolmlundPettersson and others, 2003) and temperature measurements (Reference SchyttSchytt, 1968; Reference Hooke, Gould and BrzozowskiHooke and others, 1983; Reference Pettersson, Jansson and BlatterPettersson and others, 2004). Figure 1 shows the cold surface layer thickness mapped in 2001 (Reference Pettersson, Jansson and HolmlundPettersson and others, 2003).

Fig. 1. The cold surface layer on Storglaciären in 2001. The filled circles and crosses indicate the location of 23 test sites where a complete set of model input data is available. Six of the sites, marked with crosses, were rejected because of numerical instabilities. The arrow indicates the location of the site giving a large discrepancy between modelled and radar-inferred CTS depth. The dashed rectangle indicates the area where spatial variations in water content were estimated by Reference Pettersson, Jansson and BlatterPettersson and others (2004). The grey area along the margin of the glacier indicates where the glacier is frozen to the bed. Contour interval is 4m.
3. Methods
Vertical velocity, snow-base temperature and mass-balance data were collected over large parts of the ablation area on Storglaciären in 2001. Water content at the CTS is taken from Reference Pettersson, Jansson and BlatterPettersson and others (2004). The aim was to provide input data to our one-dimensional model for a set of 23 test sites (Fig. 1), and also to enable a comparison between the spatial distribution of the different forcing parameters and the observed spatial distribution of the cold surface layer thickness. To facilitate visual comparison between the different datasets, all collected data were interpolated onto spatial grids (20 x 20 m) using kriging interpolation (e.g. Reference Deutsch and JournelDeutsch and Journel, 1998).
3.1. Emergence velocity
Emergence velocities were estimated from measurements of the vertical velocity of stakes in a 100 x 100 m grid over the entire ablation area. Surveys of the stakes were made using the differential global positioning system (GPS) between July 2000 and July 2001. The roving GPS receiver was placed on top of stakes using a specially designed holder. In addition to the instrument accuracy of ±11 mm (±10 mm ± 1 ppm of baseline length), there is an estimated survey precision error of ±10mm due to vibration of the stake when surveying. Thus, the total horizontal position error is ±15 mm. The vertical accuracy is ±21 mm (±20 mm ± 1 ppm of baseline length). These errors are negligible since they constitute about 0.15% of the average horizontal movement and 2.0% of the vertical movement. The measured vertical displacement, w, of the stakes was corrected for the local surface slope, α, which was calculated from a digital elevation model of the glacier. The resulting emergence velocity, we, is calculated using the relation we = –we þ tan α and is a measure of the upward flow of ice (Reference PatersonPaterson, 1994, p. 258).
3.2. Ice surface temperatures
In mid-April 2001, before the start of melting, we measured the temperature at the ice surface at 34 sites distributed over the ablation area using a PT-100 temperature sensor mounted in the tip of a probe that was pushed through the snow cover. The sensor has an accuracy of ±0.1 °C. The temperature measurements were recorded every 30 s and stored in 5 min averages. Before starting any measurements, we left the sensor at the snow base to reach a stable temperature. This technique is widely used in studies of the spatial distribution of permafrost (Reference Haeberli and GletscherkdHaeberli, 1973; Reference HoelzleHoelzle, 1996). The measured bottom temperature of the snow cover (BTS) is stable through the whole winter provided that the snow cover is sufficiently thick (>0.8m) to insulate the underlying ground from high-frequency variations in air temperature (Reference GoodrichGoodrich, 1982). The snow-cover thickness at all our sites was >1 m. Time-series measurements of the temperature at the snow–ice interface on Storglaciären show that the temperature drops fairly rapidly from melting conditions in the autumn and remains constant through the winter as soon as the snow cover becomes a few decimetres thick (R. Hock, unpublished data). Similarly, there is a rapid rise in temperature in the spring when melting starts (Reference Hooke, Gould and BrzozowskiHooke and others, 1983; R. Hock, unpublished data). Thus to simulate the annual temperature cycle at the surface, we use a step function with the measured BTS as minimum temperature and a period of 4 months with melting conditions as input to the model.
3.3. Water content at CTS
The water content at the CTS is generally unknown, and water-content values quoted in the literature suggest large variations (Reference Vallon, Petit and FabreVallon and others, 1976; Reference Macheret, Moskalevsky and VasilenkoMacheret and others, 1993; Reference Murray, Stuart, Fry, Gamble and CrabtreeMurray and others, 2000). However, in a small area in the upper part of the ablation area of Storglaciären, Reference Pettersson, Jansson and BlatterPettersson and others (2004) estimated the water content at the CTS at three points using ice temperature measurements across the CTS and the boundary condition at the freezing front. They also extrapolated the absolute determinations to an area of ~100 x 600 m using relative backscattered strength in ground-penetrating radar signals. The extrapolated water content is an average of the water content in the uppermost 2 m below the CTS.
The water content at our test sites was assumed to be 0.8%, which is the mean value of the three calibration points for the extrapolated water content presented by Reference Pettersson, Jansson and BlatterPettersson and others (2004). However, four of our test sites lie within the area where Reference Pettersson, Jansson and BlatterPettersson and others (2004) extrapolated the water content, giving a better estimate of the water content at the CTS (Fig. 1).
3.4. Mass balance
Detailed mass-balance measurements have been conducted annually on Storglaciären since 1945/46. The winter balance is measured in a fixed regular 100 x 100 m grid over the glacier, while the summer balance is determined from traditional stake measurements on a semi-regular stake net comprising 40–60 stakes (Reference Holmlund and JanssonHolmlund and Jansson, 1999). The distributed net balance is found by combining the winter and summer balance at each grid node in an interpolated grid (Reference JanssonJansson, 1999). Mass balance varies from year to year. To give a more representative spatial distribution of the mass-balance parameters, we use the average values for the period 1996–2001.
3.5. Model description
The temperature distribution in cold ice is governed by the temperature at the ice surface, heat diffusion and ice advection (Reference Carslaw and JaegerCarslaw and Jaeger, 1986; Reference GreveGreve, 1995). The one-dimensional temperature distribution as a function of time, t, and depth, z, is described by
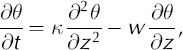
where K is the thermal diffusivity, θ is the temperature and w is the vertical advection velocity. We ignore any temperature dependence of K, which is reasonable since the temperature in the cold surface layer does not vary by more than 5°C (Reference SchyttSchytt, 1968; Reference Pettersson, Jansson and HolmlundPettersson and others, 2003). The boundary conditions for the temperature profile are the ice surface temperature and the melting temperature at the CTS. We ignore effects from a decrease in melting point with increased pressure and set the melting point temperature to 0°C, which is justified by the fact that the cold surface layer is relatively thin and any effect would be small. At the base of the cold surface layer, temperate ice is advected towards the surface and is cooled. As the ice cools, the liquid water in the temperate ice freezes and releases heat, which is transported towards the surface by advection and diffusion. The one-dimensional transition condition at the CTS is
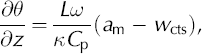
where L is the latent heat of fusion, Cp is the specific heat capacity of ice, am is the migration velocity of the CTS, w ctsis the vertical ice velocity at the CTS, дθ/дz is the temperature gradient on the cold side of the CTS and ω is the fraction of liquid water in the temperate ice arriving at the CTS. Changes in the vertical position of the CTS can be found from Equation (2) if we prescribe the temperature gradient at the CTS, the water content and the vertical velocity. The temperature distribution and the temperature gradient at the CTS can be found by integrating Equation (1), but the water content, vertical velocity and boundary conditions for the temperature profile must be assumed or taken from measurements.
We used the Crank–Nicholson finite-difference method (Reference GarciaGarcia, 2000) to numerically solve Equation (1). To simplify the numerical solution we applied a transformation to the spatial z coordinate
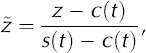
where s(t) and c(t) denote the surface and CTS positions, respectively, at time t. The z axis is positive upwards and set equal to zero at the glacier bed. The transformation remaps the cold surface layer thickness onto unity, which gives the advantage that the same numerical scheme can be used for all calculations (Reference JenssenJenssen, 1977). In the discretization, the cold surface layer is divided into 30 layers of equal thickness. Details of the transformation are given in the Appendix. The transformation of Equation (1) yields
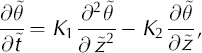
where K1 and K2 are given by
and
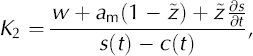
where дs/дt is any change in surface position with time, which in turn is given by the balance between net ice loss due to surface ablation and the replenishment by ice emerging from the interior of the glacier. In this study, we assume steady-state mass-balance conditions and thus use дs/дt — 0 or bn + we — 0, where bn is the net mass balance, to allow the model to reach steady state. However, we will assess the effect of дs/дt — 0 in a more descriptive way.
The transition condition at CTS (Equation (2)) must also be transformed. Rewriting the transformed transition condition gives the position change of the CTS as
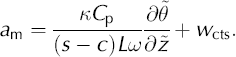
The vertical velocity, wcts, varies with depth and in a first approximation is considered proportional to the distance from the glacier bed with w — 0 at the bed and w — we at the surface (Reference HookeHooke, 1998, p. 58). The ice thicknesses for the 23 test sites used in our study are taken from ice thickness maps (Reference Herzfeld, Eriksson and HolmlundHerzfeld and others, 1993).
As an initial condition, we use a linear temperature profile prescribed by the ice surface temperature and the melting condition at CTS. An initial position of the CTS is chosen to be 75% of the ice thickness. Other initial positions of the CTS give identical results but in most cases require a longer time to reach equilibrium. For each time-step, the temperature gradient at the CTS is estimated from the vertical temperature profile. A new position of the CTS is calculated from Equation (7) using the vertical velocity and water content of the temperate ice at CTS. The vertical velocity is updated for the new CTS configuration, and the vertical temperature profile is calculated for the next time- step. From the obtained temperature profile, the temperature gradient at the CTS for the next time-step is calculated. If none of the input parameters changes with time, the CTS reaches an equilibrium depth. We can estimate the sensitivity of the cold surface layer to variations on the forcing by prescribing a time-dependent change to any of the input parameters.
3.6. Model experiments
We undertook a sensitivity analysis to investigate the relative importance of the input parameters for the cold surface layer thickness. The different tests were performed by consecutively shifting the value of parameters by a certain amount and then running the model to equilibrium. The range of values of the vertical velocity and the ice surface temperatures were taken from minimum and maximum values measured on Storglaciären. The limits for the water content were taken from common values reported in the literature (see compilation of values in Reference Pettersson, Jansson and BlatterPettersson and others, 2004). The limits used in the model experiment are shown in Table 1.
Table 1. The data limits for the sensitivity test
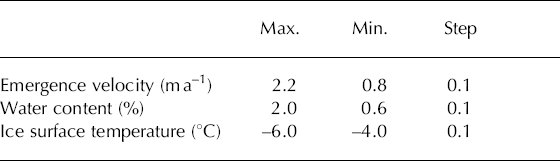
To understand the thinning and pattern of thinning of the cold surface layer on Storglaciären we also need information on the response time for perturbations of the different parameters. We tested the transient response to perturbation in the different input parameters by starting from an equilibrium condition for the CTS, applying a sudden change of a parameter value and then allowing the model to run to a new equilibrium.
4. Results
The emergence velocities derived from the stake measurements are shown in Figure 2. The velocity shows a clear increase in the middle part of the ablation area where the glacier flows over a bedrock threshold. Higher emergence velocities are also found south of the glacier centre line. The lowest emergence velocities are found close to the equilibrium line and in the northwestern part of the study area where a local accumulation area exists. The interpolated BTS over the ablation area is shown in Figure 3. The measured BTS values have a mean temperature of –4.1°C and a standard deviation of ±0.6°C, with the highest temperatures over the bedrock threshold. The net mass balance and winter net mass balance of Storglaciären over the period 1996–2001 are shown in Figure 4. During this period the net mass balance was –0.3mw.e. The larger negative net mass balance in the area where the glacier flows over a bedrock threshold, is due to the low winter net mass balance in the same area, allowing more melting of ice during the summer. The higher winter mass balance down- glacier from this area is caused by the accumulation of drifting snow as the glacier becomes steeper after flowing over the bedrock threshold, creating a lee effect (Fig. 4b). This higher winter accumulation results in less melting of ice during the ablation season and consequently lower net loss of ice (Fig. 4a).

Fig. 2. Calculated emergence velocities. The dots show the location of the ice velocity stakes used to calculate the emergence velocities. Contour interval is 0.2 ma–1.

Fig. 3. Measured snow-base temperatures in mid-April 2001. The dots show all locations where the BTS was measured. Contour interval is 0.1 °C.

Fig. 4. Average net mass balance and winter net mass balance on Storgỉaciären in 1996-2001 (data from Tarfala Research Station). Contour interval is O.2mw.e.
An example of modelled temperature profiles at two sites is shown in Figure 5 indicating that the CTS reaches much deeper than the annual winter ‘cold wave’ at all our test sites. The temperature profiles are calculated for a cold surface layer in steady state.

Fig. 5. Equilibrium temperature profiles during one year at two of the test sites with different cold surface layer thicknesses. The solid line is from a test site in the upper part of the ablation area, where the thickest cold surface layer is found. The dashed line is from a test site near the bedrock threshold, where the thinnest cold surface layer is found. The two curves are the minimum and maximum variations during the year.
The modelled time-dependent evolution of the CTS depth at five selected sites is illustrated in Figure 6;the values are similar for the other 18 sites. However, the results at six of the sites, located close to the glacier margin (Fig. 1), were rejected since equilibrium could not be reached, as a consequence of numerical instability of the model at shallow ice depths. The initial drop in CTS depth in Figure 6 is a result of the initial linear temperature gradient through the cold layer. The strong temperature gradient causes the CTS to migrate downward rapidly, but as the temperature profile evolves towards steady state, the gradient decreases and the migration of the CTS slows.

Fig. 6. Temporal evolution of the CTS as the simulation approaches steady state. The arrows indicate the radar-inferred CTS depth at each test site. (The numbers 18s3, 16s3, etc. are the test site identifiers.)
The correlation between the simulated equilibrium CTS depths and the surveyed cold surface layer thickness (Reference Pettersson, Jansson and HolmlundPettersson and others, 2003) is shown in Figure 7. The correlation coefficient is R2 = 0.79 when using a water content of 0.8% for all sites, while it becomes R2 = 0.81 when using the extrapolated water content for the test sites lying within the area of extrapolated water contents (Fig. 1). An outlier is evident, but the reason for it is unclear. This site is located close to the bedrock threshold (Fig. 1), where the measured emergence velocity was high compared with surrounding measurements, suggesting a measurement error.

Fig. 7. Correlation between simulated and radar-inferred CTS depths. An outlier is evident, marked with an arrow. The equilibrium depths for the four sites within the area of extrapolated water content are shown with triangles. The open triangles show equilibrium depth using the extrapolated water-content values, while the filled triangles indicate values calculated with 0.8% water content.
The equilibrium depth of the CTS at different values of the model parameters is shown in Figure 8. The cold surface layer thickness increases with a decreasing emergence velocity, but the increase is more pronounced when the temperature or the water content is low (Fig. 8a). A decrease in ice surface temperature results in an increased CTS depth, with deeper CTS at low emergence velocities and water contents (Fig. 8b–c).

Fig. 8. Equilibrium depth of the CTS calculated for different ranges of ice surface temperature, water content and emergence velocity, assuming a total ice thickness of 200 m.
The results from the response-time tests (Fig. 9) show that the cold surface layer thickness reacts almost instantaneously to changes in ice advection and water content, whereas a jump in ice surface temperature causes a more gradual change in cold surface layer thickness. The gradual response time for a perturbation in the ice surface temperature is expected since the temperature profile through the cold surface layer must start to adapt to the new boundary conditions before any changes in the CTS depth occur. These tests also reveal that the response time seems to be much longer for low emergence velocities than for higher velocities, while remaining similar for different values of water content and ice surface temperatures. The difference between the equilibrium CTS depths also seems to be larger for low emergence velocities and water contents, compared with higher values.

Fig. 9. A plot matrix for the results of the sensitivity test. Ts is ice surface temperature, we is emergence velocity and ω is water content. Each row in the plot matrix shows a sudden jump in one parameter, while keeping the other two constant. The columns in the plot matrix show different values of one of the constant parameters. For example, the upper left plot shows a jump in Ts of 1 °C while keeping we constant and the three curves are three different constant values of ω. In the upper middle plot there is also a jump in Ts , but keeping ω constant at 1% and the three curves show different constant values of we. The circles and filled circles show the time to reach 50% and 98% of the new equilibrium depth, respectively.
5. Discussion
The simulated CTS depth compared with measured cold surface layer thickness shows a correlation of R2 = 0.81 (Fig. 7). The scatter may be explained partly by the fact that the cold surface layer is not in equilibrium, as shown by repeated ground-penetrating radar surveys (Reference Pettersson, Jansson and HolmlundPettersson and others, 2003), and partly because the water content is prescribed to be 0.8% at all test sites, giving an uncertainty in the modelling result. Variations of the water content with ±0.2% are required to align the calculated equilibrium depths with the correlation line (R2 = 1). The extrapolated water content at CTS given by Reference Pettersson, Jansson and BlatterPettersson and others (2004) has a standard deviation of ±0.26% indicating that some of the scatter in Figure 7 may be explained by spatial variations in water content. The one-dimensional model does not consider horizontal advection and diffusion processes, which may also influence the results. Nevertheless, the good correlation between modelled and observed CTS depths indicates that our model captures the major physical processes influencing the cold surface layer thickness.
The CTS reaches much deeper than the annual winter ‘cold wave’ and seems not to be dependent on a direct cooling diffusion of the ‘cold wave’ (Fig. 5). This is simply because heat will continually be transported away from the ‘warmer’ temperate ice towards the colder surface as long as the temperature gradient is strong enough. This is determined by the mean annual surface temperature. The modelled temperature profiles closely resemble the measured temperature profiles from the cold surface layer on Storglaciären and elsewhere (Reference Ødegard, Hamran, Bø, Etzelmuller, Vatne and SollidØdegård and others, 1992; Reference BjornssonBjörnsson and others, 1996; Reference Pettersson, Jansson and BlatterPettersson and others, 2004), supporting our assertion that our model captures the major physical processes.
The specific aim of this study is to improve our understanding of the variability of the cold surface layer thickness and the causes of thinning and the thinning pattern observed on Storglaciären. Hence, we discuss (1) the sensitivity of the different forcing parameters and their spatial distribution to assess their relative importance for the spatial distribution of the cold surface layer depth and (2) any time-dependent variation in the forcing parameters that could explain the observed thinning of the cold surface layer.
5.1. Spatial pattern of the cold surface layer
In order to explain the spatial pattern of the cold surface layer thickness on Storglaciären, we need to assess relative importance of the forcing mechanisms. The model sensitivity experiments suggest that the cold surface layer is highly sensitive to variations in vertical advection, where low vertical velocities lead to a thick cold surface layer (Fig. 8). Variations in water content also influence the cold surface layer thickness considerably, especially for low water content (<1%). Altogether, this suggests that we should find the thickest cold surface layer in areas with low emergence velocity, low water content, low ice surface temperature or a combination of these factors.
The following is a comparison of the distribution of cold layer thickness over the glacier (Fig. 1) with our measured BTS, emergence velocity, net mass balance and the water- content distribution given by Reference Pettersson, Jansson and BlatterPettersson and others (2004).
The distributed BTSs (Fig. 3) show some similarities with the cold surface layer thickness (Fig. 1). Areas with a high BTS coincide with areas having a thin cold surface layer, while a thicker cold surface layer is associated with a low BTS. This correlation seems reasonable since low ice surface temperatures would result in stronger cooling of the ice during winter, leading to a thicker cold surface layer.
The water content given by Reference Pettersson, Jansson and BlatterPettersson and others (2004) covers only a small portion of the upper part of the ablation area. They identified an area of low water content south of the kinematic centre line, while higher water content coincides with the northern edge of the glacier. The area with low water content coincides with an area of thin cold surface layer, and high water content to the north is associated with a thick cold surface layer. Our model results of the steady-state cold surface layer thickness show that lowering the water content, while keeping all other parameters constant, results in a thicker cold surface layer. This is in contrast to what we find when comparing the spatial distribution of water content of Reference Pettersson, Jansson and BlatterPettersson and others (2004) with the cold surface layer thickness. This suggests that the water content is not the main factor behind the spatial pattern of the cold surface layer thickness.
The patterns of emergence velocity (Fig. 2) and cold surface layer thickness (Fig. 1) show close similarities. For example, the small areas with very thin cold surface layers in the central parts of the ablation area agree well with areas of high emergence velocities. The high emergence velocities south of the centre line in the upper part of the ablation area are probably the reason for the thin cold surface layer in this region, despite the low estimated water content in the same area. This suggests that the cold surface layer thickness pattern is strongly influenced by the vertical advection and indirectly by factors controlling the vertical advection. This is supported by the model results which show that for high emergence velocity (>1.5 m a–1), the cold surface layer becomes relatively thin even if the water content is low (Fig. 8a). However, this might not be true in areas where the vertical advection is low. A water content of <1% and an emergence velocity of <1 m a–1 seems to have a comparable impact on the CTS depth (Fig. 8a).
The net mass-balance pattern in Figure 4a shows close similarities with the pattern of cold surface layer thickness (Fig. 1). The cold surface layer is thinnest in areas with large negative net ablation. This is expected, since removal of ice at the surface is the only efficient way to thin the cold surface layer.
In summary, the apparent relationship between emergence velocity, net ablation and CTS depth together with the strong model response to these parameters suggest that the variations in thickness of the cold surface layer observed on Storglaciären are mainly controlled by ice flow and mass balance.
5.2. Causes of thinning of the cold surface layer
The thinning of the cold surface layer observed between 1989 and 2001 on Storglaciären could be either the result of a recent change or part of long-term variability in the forcing of the cold surface layer. To understand the timescale on which a change in the forcing of the cold surface layer may have occurred, we must assess the response time for perturbations in the forcing.
The modelled response time to reach equilibrium after perturbation of water content or a surface temperature change of 1°C is 10–30 years, provided that the emergence velocity is relatively high (Fig. 9). At low emergence velocities, the response time is much longer, ~100 years. The longer response time is due to the fact that the migration of the CTS occurs mainly through diffusion of heat instead of convection of temperate ice. Naturally, the response time depends on the amplitude of the perturbation, but for any reasonable changes in the forcing the results suggest that the cause of the cold surface layer thinning on Storglaciären probably has occurred during the last ~50 years.
The recorded mass balance on Storglaciären shows that the average annual net mass balance has increased from –0.8 m w.e. a–1 to +0.3 m w.e. a–1 for the period 1945–95 as a result of decreased ablation and increased accumulation (Reference Holmlund, Karlen and GruddHolmlund and others, 1996a). However, during the past few decades the glacier has been in a quasi-steady state, with the net mass balance close to equilibrium (Reference HolmlundHolmlund, 1988; Reference Holmlund and JanssonHolmlund and Jansson, 1999). This suggests that no significant increase in loss of ice at the surface has occurred during recent decades that could cause the thinning of the cold surface layer.
The mass-balance studies on Storglaciären show a tendency to increased total winter accumulation (Reference Holmlund, Karlen and GruddHolmlund and others, 1996a). This increase in snow-cover thickness would further insulate the ice surface from the cold winter air and hence influence the temperature profile in the cold surface layer. The spatial distribution of the accumulation for the period 1945–2000 shows that the increase is small in the ablation area (<0.1 m w.e.), while most of the increase has occurred in the accumulation area (Jansson and Pettersson, in press;Tarfala Research Station, unpublished data). This suggests that the thinning is not induced by increased insulation of the ice from the low winter temperatures.
Measurements of the emergence velocity along the centre line on Storglaciären made in 1965–67 (Reference SchyttSchytt, 1968), 1983–85 (Reference Hooke, Calla, Holmlund, Nilsson and StroevenHooke and others, 1989) and our data from 2001 are very consistent (Jansson and Pettersson, in press). This reflects the fact that Storglaciären has been in a quasi-steady state since the 1970s (Reference Holmlund and JanssonHolmlund and Jansson, 1999) and suggests that the thinning of the cold surface layer is not likely to be the consequence of a considerable change in the flow regime of the glacier.
Variations in the water content of ice that arrives at the CTS could cause changes in the cold surface layer thickness. Our estimates of water content are point measurements or averages over very short depth intervals in the uppermost part of the temperate ice below the cold surface layer. Since the average vertical velocity is 1 m a–1 in the ablation area of Storglaciären, it is possible that the water-content values are inaccurate over longer periods, depending on how the water content varies with depth. Information about variations in water content with depth are very limited. Reference Murray, Stuart, Fry, Gamble and CrabtreeMurray and others (2000) used radar tomography in a borehole on a temperate Icelandic glacier to show that the water content can vary with depth by ±1% within the major body of the ice. The cause of this variation is not fully understood. Reference PatersonPaterson (1971) and Reference Pettersson, Jansson and BlatterPettersson and others (2004) suggest that the most important source of liquid water in temperate ice is the entrapment of water at the firn–ice transition in the accumulation area. Thus, changes in the entrapment processes due to climatological and glacier geometrical changes in the accumulation area could lead to time- dependent and spatial variations in the water content of the ice. Storglaciären underwent major thinning due to climatic warming at the beginning of the 20th century (Reference HolmlundHolmlund, 1993), so, it is likely that the water content has changed both spatially and temporally. A change in entrapment of water in the accumulation area would not result in a simultaneous change in water content at the CTS over the whole ablation area since ice becomes older towards the terminus due to longer flow paths. If a change in water content was responsible for the thinning of the cold surface layer, we would expect a gradual change in thinning towards the terminus. Such gradual thinning is not observed (Reference Pettersson, Jansson and HolmlundPettersson and others, 2003), but it is not possible to rule out the thinning of the cold surface layer being caused by changes in water content in the ice arriving at the CTS.
Past changes in the ice surface temperature during winter can be estimated from the nearby meteorological station at Tarfala Research Station where hourly air temperatures have been recorded since 1965 (Reference Grudd and SchneiderGrudd and Schneider, 1996). The recorded summer temperatures show a slight decrease during the whole period, but a significant increase in winter temperatures (October–April) of about 1°C occurring since the mid-1980s (Reference Grudd and SchneiderGrudd and Schneider, 1996), which also would affect the ice surface temperature. However, it is not certain that an increase in air temperature leads to an identical increase at the snow–ice interface, because of the damping effect caused by the snow cover.
A 1°C increase in BTS will lead to a change in the upper boundary conditions for the temperature profile through the cold surface layer, resulting in thinning of the cold surface layer. Increasing the temperature boundary condition in the model by 1 °C, but keeping all other measured parameters unchanged, results in a decrease of the CTS depth of 3–12 m depending on the water content and the emergence velocity (Fig. 8). A comparison between these results and radar- inferred CTS depth in 1989 shows a correlation of R 2 = 0.87 (Fig. 10). This indicates that an increase in BTS of 1°C explains most of the observed change in the cold surface layer. However, an increased BTS will not lead to a thinner cold surface layer; it will only slow the freezing rate at the base of the cold surface layer since the temperature gradient, and hence the heat conduction from the CTS, would decrease. Consequently, the thinning of the cold surface layer is probably caused by a stronger imbalance between freezing at the base of the cold surface layer and the net loss of cold ice at the surface.

Fig. 10. Correlation between simulated and radar-inferred CTS depths in 1989. The simulated CTS depths are calculated using the same input as in Figure 7, but lowering the ice surface temperature by 1°C.
5.3. Pattern of thinning of the cold surface layer
The thinning of the cold surface layer is small in an area over the bedrock threshold separating the lower and upper ablation area and south of the kinematic centre line in the upper part of the ablation area (Reference Pettersson, Jansson and HolmlundPettersson and others, 2003). The areas with small thinning coincide with areas with high emergence velocity, although the agreement is not perfect. Figure 9 indicates that an increase in ice surface temperature or water content would give a larger change in CTS depth at low emergence velocities than at higher velocities. This suggests that areas with a low emergence velocity would react strongly to an increase in ice surface temperature and thin more than areas with a high emergence velocity. For example, the model results show that an increase in ice surface temperature of 1°C causes thinning of the cold surface layer of ~2m in areas with an emergence velocity of 2 m a–1, while areas with low emergence velocities (1 m a–1) have a thinning of ~8m (Fig. 8b). This suggests that spatial variations in emergence velocity could be the primary cause of the thinning pattern of the cold surface layer.
6. Conclusions
The equilibrium depth of the CTS given by our onedimensional thermomechanical model of the cold surface layer thickness shows good correlation with observed CTS depth, indicating that the major physical processes are well described by the model. The least-known input parameter is the water content of the temperate ice arriving at the CTS. Uncertainties in water content used in the model at the different test sites or the fact that the current CTS is not in equilibrium with present forcing could explain the discrepancies between simulated and radar-inferred CTS depths.
The pattern of cold surface layer thickness is similar to the distribution of emergence velocities calculated from ice velocity measurements as well as the average (1996–2001) net loss of ice at the surface. This suggests that vertical advection and surface melting are the most important forcing components for the spatial pattern in thickness of the cold surface layer. This is supported by thermomechanical modelling of the cold surface layer, which shows strong sensitivity of the cold surface layer thickness to changes in vertical advection rates. The spatial distribution of water content of the temperate ice at CTS cannot explain the variability of cold surface layer thickness. However, information about the spatial distribution of water content is limited.
Model sensitivity studies show that the cold surface layer thickness reaches steady state within a few decades following a perturbation in the forcing in the range of observed variations. Thus, the cause of the observed thinning on Storglaciären probably occurred during the past few decades. No significant change in the mass balance or ice flow of Storglaciären has been reported that could explain the observed thinning of the cold surface layer. We cannot exclude the possibility that the thinning is caused by a time-dependent change in water content that arrives at the CTS due to variation in water content with depth. However, in this case, the thinning pattern would be different from the observed pattern. Instead, thinning of the cold surface layer is probably caused by an increased winter air temperature since the mid-1980s. Rerunning the model with a 1 °C lower BTS while keeping all other input parameters unchanged gives equilibrium CTS depths in good agreement with the radar-inferred CTS depths in 1989. Thus an increase in ice surface temperature of 1°C would explain most of the observed change of the cold surface layer. An increased winter air temperature changes the upper boundary condition for the temperature distribution in the ice. This change leads to a reduced freezing rate at the base of the cold surface layer. Thus, the thinning is caused by a stronger imbalance between freezing at the base of the cold surface layer and the net loss of cold ice at the surface.
Our model results suggest that the cold surface layer thins considerably more in areas with low emergence velocity (>1 ma–1) than in areas of higher velocities. Comparing the observed cold surface layer thinning pattern with our measured emergence velocities shows that areas with the smallest cold surface layer thinning coincide with areas with high emergence velocity. This suggests that spatial variations in emergence velocity could be the cause of the observed complex thinning pattern of the cold surface layer.
Acknowledgements
We thank K. Halkola and E. Kuriger for assistance with ice velocity measurements. R. Hock, J.-O. Näslund, P. Holmlund and R.W. Jacobel provided valuable comments on the manuscript. We thank H. Björnsson, an anonymous reviewer and Scientific Editor J. Glen for valuable comments. Financial support from the Axel Lagrelius Fund and the Göran Gustavsson Foundation is acknowledged.
Appendix
Coordinate Transformation
Due to the transformation z → where
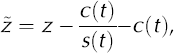
the transformed coordinate derivatives become

and
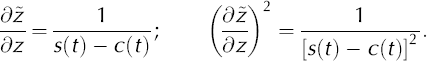
The transformed temperature scalar field can be rewritten as
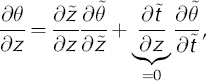
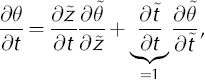
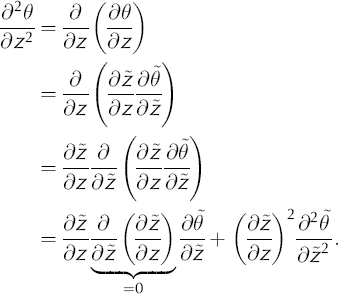
Substituting the transformed derivatives into the onedimensional temperature-distribution equation (Equation (1)) yields
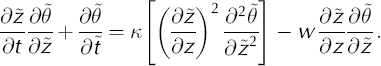
Thus
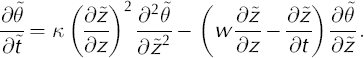
Substituting the transformed coordinate derivatives (Equations (A1) and (A2)) yields
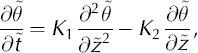
where K1 and K2 are
and
















