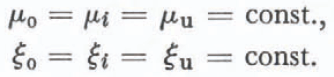Hostname: page-component-848d4c4894-v5vhk Total loading time: 0 Render date: 2024-06-30T17:54:27.518Z Has data issue: false hasContentIssue false
  • English
  • Français

Observed Maximum Run-Out Distance of Snow Avalanches and the Determination of the Friction Coefficients µ and ξ

Published online by Cambridge University Press:  20 January 2017

Othmar Buser  and
Hans Frutiger
Othmar Buser
Affiliation:
Eidg. Institut für Schnee- und Lawinenforschung, CH-7260 Weissfluhjoch/Davos, Switzerland
Hans Frutiger
Affiliation:
Eidg. Institut für Schnee- und Lawinenforschung, CH-7260 Weissfluhjoch/Davos, Switzerland
Rights & Permissions [Opens in a new window]

Abstract

To fix the limits of different hazards in the avalanche-hazard maps one uses criteria pertaining to avalanche dynamics. These criteria are at present the velocity and the run-out distance of a given avalanche for a given place. In 1955 A. Voellmy published his theory of avalanche dynamics which has widely been used in practical map preparation. Since 1962 his equations have also been used by the Eidg. Institut für Schnee- und Lawinenforschung (EISLF) to calculate avalanche pressures and run-out distances. Furthermore B. Salm (EISLF) developed another equation for the calculation of run-out distances in 1978. Both the equations of Voellmy and of Salm contain two friction coefficients, µ and ξ. Little is known about them and opinions, even among specialists, differ on what values should be given to them.

This paper presents field observations on very long run-out distances. These observations are used to calculate values for pairs of µ and ξ. For avalanche zoning, only extreme values are of interest, i.e. very low values for µ and very high values for ξ. For the calibration of those coefficients, ten avalanches from the winters 1915–16, 1967–68, 1974–75, and 1977–78 have been used. Those avalanches occurred during heavy and intense snowfalls. For those avalanches, the pair µ= 0.155, ξ = 1 120 m/s2 was found for the Voellmy equation and the pair µ = 0.157, ξ =1 067 m/s2 for the Salm equation. These values only partially agree with those used up to date by EISLF. It is recommended for example that for extreme flowing avalanches (newly fallen snow, soft slabs) the pair µ = 0.16,ξ = 1 360 m/s2 be used.

Résumé

Résumé

On se sert de critères de la dynamique d’avalanches pour délimiter les différentes zones de la carte du danger d’avalanches. Ces critères sont, en particulier, la vélocité et la distance d’arrât de l'avalanche. En 1955, A. Voellmy a publié une dynamique d’avalanches qui a trouvé une vaste application dans la pratique de l’établissement des cartes du danger d’avalanches. Les équations sont appliquées depuis 17 années par l’Institut Suisse Fédéral pour l’Étude de la Neige et des Avalanches (ISFENA) pour calculer les forces dynamiques des avalanches et leur distance d’arrêt. En 1978, B. Salm (ISFENA) a ajouté une autre équation pour calculer la distance d’arrêt. Non seulement dans les équations de Voellmy, mais aussi dans l'équation de Salm apparaissent les facteurs de frottement µ et ξ. On ne sait que peu de choses de leurs valeurs numériques et même dans les milieux d'experts les opinions sur ces valeurs diffèrent.

Dans cette publication sont présentées dans observations sur des distances d’arrêt extraordinaires. En outre, ces observations servent pour les calculations des valeurs numériques des facteurs de frottement. Pour les cartes du danger d’avalanches, seules les avalanches extrêmes nous intéressent. Cela veut dire que la présente étude ne considère que les valeurs extrêmes de µ et ξ. Pour la détermination des valeurs des deux facteurs de frottement, on s’est servi des observations portant sur dix avalanches descendues au cours des hivers 1915-16, 1950-51, 1967-68, 1974-75 et 1977-78, à la suite de grosses et intenses chutes de neige. De ces avalanches résultent les paires de facteurs de frottement µ = 0,155, ξ = 1 120 m/s2 pour l'équation de Voellmy, et µ = 0,157, ξ=1 067 m/s2 pour l’équation de Salm. Ces valeurs ne s’accordent que partielle- ment avec celles dont on a fait usage jusqu’à présent à l’Institut. Il est recommendé d’appliquer, par exemple, la paire µ = 0,16, ξ= 1 360 m/s2 pour la calculation des avalanches coulantes extrêmes, constituées de neige fraîche (plaques de neige molle).

Zusammenfassung

Zusammenfassung

Bei der Bearbeitung von Lawinengefahrenkarten braucht man für die Abgrenzung von Flächen verschieden starker Gefährdung lawinendynamische Kriterien. Dies sind vor allem die Geschwindigkeit und die Auslauf- strecke der Lawinen. Im Jahre 1955 hat A. Voellmy eine Lawinendynamik veröffentlicht, die in der Praxis weit verbreitet Anwendung gefunden hat. Seine Gleichungen werden seit 17 Jahren auch vom EISLF gebraucht, um die Lawinenkräfte und Auslaufstrecken zu berechnen. Zudem hat B. Salm (EISLF) 1978 eine weitere Gleichung zur Berechnung von Auslaufstrecken aufgestellt. In den Gleichungen sowohl von Voellmy als auch von Salm treten zwei Reibungsparameter µ und ξ auf. Über deren Zahlenwerte ist nur wenig bekannt und in Fachkreisen gehen die Meinungen darüber zum Teil auseinander.

In der vorliegenden Arbeit werden Beobachtungen über ausserordentlich grosse Auslaufstrecken mitge- teilt. Zudem werden die Beobachtungen dazu benützt, um Zahlenwerte für die Reibungsparameter zu berechnen. Für die Bearbeitung von Lawinengefahrenkarten interessieren nur die Werte extremer Lawinen, d.h. untere, respektive obere Extremwerte für µ und ξ. Für die “Eichung” der Reibungsbeiwerte wurden zehn Lawinen verwendet, die in den Wintern 1915-16, 1950-51, 1967-68, 1974-75 und 1977-78 während ausserordentlich grossen und intensiven Schneefällen niedergingen. Für diese Lawinen ergibt sich das Wertepaar µ= 0,155/ξ = 1 120 m/s2 für die Gleichung nach Voellmy und µ = 0,157 / ξ = 1 067 m/s2 für die Gleichung nach Salm. Diese Werte stimmen nur teilweise mit den bis jetzt vom EISLF verwendeten Werten überein. Es wird empfohlen, für extreme Fliesslawinen (Neuschnee; weiche Schneebretter) zum Beispiel das Wertepaar µ = 0,16/ξ= 1 360 m/s2 zu verwenden.

Type
Research Article
Information
Journal of Glaciology , Volume 26 , Issue 94 , 1980 , pp. 121 - 130
Copyright
Copyright © The Author(s) 1980 

Concerns and objectives

In the last 15 years, from 1964 to 1978, the Eidg. Institut für Schnee- und Lawinen- forschung prepared 26 so-called Avalanche Hazard Maps (AHM). These maps display graphically the avalanche hazard for a given region, i.e. usually for the whole territory of a municipality (Reference FrutigerFrutiger, 1980).

In 1975 the Swiss issued guidelines (Switzerland, Bundesamt für Forstwesen, 1975) for the preparation of those maps which are the technical base for avalanche zoning. The rules that govern the preparation of those maps are given in the guidelines as follows:

The AHM is to be prepared by observing strongly objective and scientific criteria. These are

  • —an evaluation of the terrain configuration and of the avalanche scars;

  • —the Avalanche Cadastre (AC), if present;

  • —the calculating technique.

The aims of the calculating technique are:

  • —to bring in evidence those potential avalanches which are not contained in the AC but might become active under extreme snow conditions;

  • —to determine run-out distances and dynamic forces quantitatively;

  • —to guarantee a uniform evaluation of avalanche hazard in different places.

Indeed, in Switzerland, all AHMs are supposed to be prepared with the aid of a calculating method. This method, of course, is only one of many aids. The equations used to determine run-out distances and dynamic forces are those published by Reference VoellmyVoellmy (1955). His work has been translated into English in 1964 and prepared for engineering application by Reference Leaf and MartinelliLeaf and Martinelli (1977).

Run-out distance and dynamic force are criteria for the separation of areas of different degree of hazard. In Switzerland, the AHMs usually show three different degrees of hazard which are coloured red (high hazard), blue (moderate hazard), and white (no hazard).

The criteria for the separation of high from moderate hazard are:

  • —the specific thrust pressure of an extreme avalanche is 30 kN/m2 and/or

  • —smaller avalanches run frequently, i.e. once in 30 years.

The criteria for the separation of moderate from no hazard is:

  • —the down-slope edge of an extreme avalanche, i.e. the reach, which is given by the run-out distance.

Essentially one has to know the velocity and density of flow of an avalanche for any given section of the path which allows calculation of the thrust pressure and the run-out distance.

One of the most intricate problems in the routine preparation of AHMs is finding the “true” or the most likely extreme run-out distance. This problem has to be solved either for long, gently sloping sections of the track or for wide, open and flat valley bottoms in the run-out zone of the path. In many cases there is no evidence of avalanching, neither from scars nor from the cadastre. In those cases the only aid in defining the above-mentioned lines between the areas of different degree of hazard will be the calculating method.

Considering that one assumes a great responsibility toward the land owners in deciding whether or not a parcel of land will be taken as safe or hazardous, it becomes evident that the method of calculation used in AHM preparation must be reliable, Voellmy’s equations are widely used in Switzerland as well as in other European Alpine countries and on the North American continent. Voellmy himself wrote in the introduction to his work (Reference VoellmyVoellmy, 1955, p. 159, translated by the present authors, as are subsequent quotations from papers in German): “In agreement with the pioneering domestic and foreign practice this report closes with an attempt to establish a highly simplified avalanche dynamics, which strives for a more qualita- tive analysis of the effects of the most important factors and may serve as a suggestion and working hypothesis for further observations and investigations”. And what Reference Leaf and MartinelliLeaf and Martinelli (1977) stated in their publication must be repeated, “field calibration is extremely important in order to build confidence in its use”.

One of the co-authors (H. Frutiger), has for many years prepared advisory reports on avalanche hazard mapping for many Swiss and foreign communities. In the last ten years, from 1969 to 1979 he prepared 17 such maps (AHMs) which cover a total area of 32 623 hectares (80 613 acres) with 378 individual avalanche paths. He has had the opportunity of collecting interesting data on exceptional (extreme) avalanching, which deserve closer inspection with regard to the calculating technique.

The objectives of this paper are, first, to present some outstanding field data on very long run-out distances. Second, with the aid of the field data it should be possible to “calibrate” the friction coefficients µ and ξ. This calibration was performed with the aid of a computer by O. Buser. There is no intention to discuss the theoretical background either of Voellmy’s formulae or of that of Reference SalmSalm (1979) for the run-out distance. The latter is not yet published. The only objective is to check the applicability in practice of the formulae as they are given with respect to the friction coefficients which need further investigation.

Concept and performance of the calibration

Voellmy gives the following equations for the maximum velocity vmax and the run-out distance s, of flowing avalanches.

(1)
(2)

Voellmy’s vmax will henceforward be called the “terminal” velocity v. To allow the flowing snow to reach a velocity near the terminal velocity, the uniformly inclined section of the starting zone or the track must be long enough. For the avalanches used in the calculations, the length of the sections varied from 130 m to 580 m thus allowing the flowing snow to reach 90% of the terminal velocity.

The Voellmy equations have been slightly altered by EISLF (B. Salm). The flow depth h' has been replaced by the hydraulic radius R for channelled avalanches and by the thickness of flow d for unconfined avalanches. The tangent of the run-out distance, tan ψu, has been replaced by sin ψu, and h m by d s, where

(3)

dP and vP are the thickness and the velocity of the flow at the point P where the gradient of the track diminishes to about 15% to 17% (9° to 10°). This is the transition from the track to the run-out zone. Since 1979 EISLF (Reference SalmSalm, 1979) has used another equation for the run-out distance. It starts from the same statements as those made by Reference VoellmyVoellmy (1955) and uses the same parameters as did Voellmy.

(4)

After the slight alterations mentioned above and some transformations, the Voellmy equations are used in the following form:

(5)
(6)

where (see Fig. 1) v is the terminal velocity of the avalanche, vp the velocity of the avalanche at the point P, s the run-out distance, R the hydraulic radius, dp the thickness of flow at the point P, is the slope of the “approach” section or “runway”; this is the section of the track uphill of P, the section must be long enough (150-600 m) to allow the avalanche to assume a velocity which is Figure 1 near to terminal velocity; ψ u is the slope of the run-out distance, µ the coefficient of kinetic friction, ξ the (inverse) coefficient of turbulent friction, g the acceleration of gravity, ρ the density, and γ the weight per unit volume, γ= ρg. The friction forces are

Fig. 1. Longitudinal profiles of avalanche paths.

In the cross-section of the avalanche track at P, R and d p depend on the magnitude and the velocity of the avalanche. The magnitude is given by the volume discharge Q, which is the number of cubic metres of snow flowing per second. The magnitude results from the depth h0 and the width b 0 of the slab breaking away and from the slope of the starting zone ψ 0 and the two friction coefficients µ and ξ. The velocity of the avalanche at the lower end of the starting zone is

(7)

and the volume-discharge is

(8)

The method of procedure is as follows. The data of observed avalanches allow us to establish a system of equations in which all parameters are known except µ and ξ. The system is then solved for μ and ξ.For this certain assumptions have to be made:

  1. 1. The volume discharge must be considered constant in any section of the track from the starting area to the run-out zone, i.e. Q 0 = Q i = const.

  2. 2. The friction coefficients must not change during the avalanching; they have to be constant with respect to time and location, i.e.

    Since we are interested only in extreme avalanches which will start only during, or shortly after, big and intense snow storms and which will consist mainly of dry, newly- fallen snow, we may consider the friction conditions very similar for all such avalanches. These are of the soft slab type.

  3. 3. It is obvious that the system of equations used to find values for µ and ξ must contain at least two different avalanches but those must have occurred under similar snow and weather conditions.

Data of ten different avalanches which occurred in the winters 1915-16, 1950-51, 1967-68, and 1977-78 were used for the calibration. The terms used in this paper for the different sections of an avalanche site are the same as those used in the publication Snow avalanche sites by Reference MartinelliMartinelli (1974). The following parameters have to be known, measured, or deduced, as exactly as possible:

  • —the depth of the slab h 0,

  • —the width of the slab b 0,

  • —the slope of the starting zone ψ 0,

  • —the slope of the “approach” section ψ,

  • —the hydraulic radius R in the case of a channelled avalanche or the thickness of flow d in the case of an unconfined avalanche,

  • —the slope of the run-out distance ψu,

  • —the length of the run-out distance s.

We consider only avalanches which ran out on a flat and wide valley bottom or had run over a long, gently sloping section of the track. We do not consider avalanches which stopped in narrow valley bottoms where ψu may become negative (opposite slope). Only fully developed, naturally released avalanches are considered.

The different gradients of a natural avalanche path are represented by a longitudinal profile (centre-line of the avalanche path). Those profiles have been carefully drawn from large-scale topographic maps at a scale 1 : 10 000 with contour intervals of 10 m. The profiles have been simplified to a polygonal traverse (Fig. 1).

For the discharge cross-section of the “approach” section simplified shapes had to be adopted. R and d are calculated from Q 0 for those shapes. The shapes are:

  • for channelled avalanches: the cross-section is an isosceles (regular) trapezium, determined by the base bT and the slope of the sides α. If b T is zero, then the shape is a triangle.

  • for unconfined avalanches: when b T is large compared with the thickness of flow d, the slope of the sides is considered to be vertical, i.e. α = 90° and the shape becomes rectangular with b T = b. For unconfined avalanches R becomes d (the thickness of flow).

The determination of some of the “known” parameters is very difficult. The magnitude of the avalanche depends, among other factors, on h 0 which should be the average slab depth over the whole starting area. It is, however, impossible to measure that value before the avalanche starts, and after it has started, h 0 vanishes. It can only be determined indirectly from the fracture face. Nevertheless, h 0 can be determined very closely from precipitation data and the increment of the snow-pack measured at nearby snow-data measuring stations. In this way, at least an upper and lower limit and a “most likely” value of h 0 can be evaluated.

The length of the run-out distance s itself is a function of µ and ξ and cannot be determined at the beginning of the compulation of µ and ξ in some cases. This happens when the slope of the track diminishes gradually and no pronounced change in gradient is present which would mark unmistakably the beginning of the run-out distance. In these cases the run-out distance was not known a priori and had to be determined by trial and error.

When considering Salm’s equation, the position of P is determined by µ. This follows from Equation (4) where µ is contained in becomes negative. Once the argument of the natural logarithm, [vp 2/(ξdsΦ*) +1],is less than 1, there is no positive solution for s. However, the Voellmy equation allows a µ which might be considerably smaller than tan ψu.

Table I. Avalanches showing extraordinarily long and gently sloping sections of track sf and long RUN-OUT DISTANCES so

In this table ψ0 is the slope of the starting zone, b 0 the width of the slab, h o the depth of the slab, ψ the slope of the “aprroach” section, b the width of the “approach”-section, ψu the slope of the run-out distance, so the observed run-out distance, and sf the length of the gently sloping track.

Field observations

Table I gives data on 20 avalanches which show long, gently-sloping sections of track or long run-out distances. Of those 20 avalanches only 10 were used to determine values of µ and ξ because some data were missing for the other avalanches which therefore could not be used for the calculations. Those data concern mostly the starting zone and snow conditions. In some cases the flow of the avalanche was influenced by obstacles like timber and buildings. In the following the most interesting data of those avalanches are briefly presented.

No. 2 Malbun/Triesenberg

In January 1951 an avalanche hit the basin-shaped valley of Malbun and destroyed several buildings. It is not known where the avalanche started. There are several potential starting zones which could have released the avalanche. The damage to the buildings and the debris of the buildings which were scattered by the avalanche on its way, however, marked unmistakably the lower section of its path. The run-out distance had a slope of 11.3% (6.4°) and was 620 m long.

No. 6 Schiatobel/Davos

This avalanche runs in a narrow, rocky ravine and ends in a built-up area of Davos called Horlauben. In the last hundred years (1879-1979) the avalanche ran to Horlauben four times, namely 23 January 1919, 4 February 1935, 17 February 1962, and 20 March 1967. The gently sloping middle track section is 700 m long and has a gradient of 18.6% (10.5 0).

No. 7 Dorftäli/Davos

The Dorftäli avalanche ran on 26 January 1968, destroyed a bridge of the Parsenn funicular and ended on the valley bottom of Davos. In the summer-house area of the Böden the avalanche destroyed several homes. Between 2 180 m and 2 300 m m.s.l. there is a gently sloping section of track which is 580 m long and which has a slope gradient of 21.4% (12.1°).

No. 8 Schattenwieseli/Davos

On 27 January 1968 this avalanche penetrated the village of Glaris. From 1 600 m m.s.l. down-slope the gradient of the track is only 23.3% (13.1°) for a distance of 300 m and subse- quently for a distance of 490 m the track gradient is only 18.4% (10.4°). For the whole distance of 790 m the mean gradient is 20.2% (11.4°).

No. 12 Val Ruschna/Scuol

On 22 February 1970 this avalanche destroyed a ski-lift station at the lower end of Val Ruschna (2 200 m m.s.l.). It is mysterious why the station was destroyed since there was nearly no avalanche snow found at the station. From that observation it is concluded that the powder flow of the avalanche must have destroyed it. The track of the avalanche up-slope of the station has a mean gradient of 26.1% (14.6°) for a length of 880 m. The lowest section immediately up-slope of the station is 400 m long with a gradient of 22.2% (12.5°).

No. 13 Pardenn/Klosters

This avalanche occurred in the back country presumably on 23 February 1970. It did heavy damage to the forest. The avalanche crossed the wide and horizontal valley bottom and damaged a mature and old spruce stand on the opposite valley shelf. It appears that the powder portion of the avalanche must mainly have caused the damage, i.e. the high thrust pressure due to high velocity. The lowermost section of the path is 660 m long with a gradient of only 7.6% (4.3°).

No. 14 Corvatsch/Silvaplana

An avalanche released artificially on 22 March 1970 hit two ratracs and caught five people, two of which were killed. The persons who participated in the artificial release obviously underestimated the potential reach of the avalanche. It ran as a wide unconfined avalanche (120 m wide). The mean gradient of the track is 24.7% (13.9°) for a distance of 850 m. The lowermost section of the path (run-out zone) had a gradient of 19.0% (10.8°) and was 420 m long.

No. 15 Leisalp/Vals

On 5 April 1975 this avalanche released in the Satteltilücke, crossed the gently sloping track section of the Leisalp, destroyed some avalanche defences (supporting structures) below and hit the village of Vals. Evidently, when those defences were planned nobody considered that the avalanche might cross the Leisalp section. That section is 900 m long with a mean gradient of 33.3% (18.4 0). The most gentle section of track has a gradient of 30.2% (16.8°) and is 430 m long.

No. 16 Piai-Carà/ Leontica

On 5 April 1975 this avalanche ran very far. It destroyed four vacation homes and caught seven persons of whom five died. The avalanche ran right into a place which had been planned to become a tourist resort. In between 1 620 m and 1 605 m m.s.l. there is a section of track, 220 m long with a gradient of only 6.8% (3.9°). The mean gradient of the section 1 620 m-1 560 m m.s.l. is 12.2% (7.00) for a distance of 470 m. The lowermost section of the path (1 620 m-1 490 m m.s.l.) is 780 m long and has a mean gradient of i6.7% (9.5°).

No. 17 Ijes/Maienfeld

A stable on the alp called Ijes had been protected from the avalanche by an earth dam built just a few metres distant from the building. On 25 January 1976 the avalanche jumped the dam and damaged the stable heavily. The mean gradient of the track above the stable is 13.9% (7.9°) for a distance of 720 m. The stable is situated at the end of a flat valley bottom which is 380 m long and shows a gradient of only 7.9% (4.5°).

These data allow us to establish, tentatively and as a working hypothesis, a relationship between slope gradient and avalanche movement as displayed in Table II.

Table II. Relationship between slope gradient and avalanche movement

Results and discussion

Table III presents the calculated values of µ and ξ. Columns 4—5 contain pairs of µ and ξ where ξ assumes values used up to date, i.e. roughly 400 m/s2 ≤ ξ ≤ 600 m/s2. The corres- ponding µ however, is less than the values used up to date, namely 0.120 to 0.126. Column 4 shows that µ, calculated according to Voellmy, may be less than the tangent of ψ uColumns 8-9 and 12-13 give the µ/ξ pairs for all avalanches except No. 18, calculated according to Voellmy and Salm, where the p is greater than the tangent of ψ uAvalanche No. 18 does not fit the series and was dropped from the calculations. The best fit of the µ/ξ pairs for the Voellmy equation is µ = 0.155,ξ = 1120 m/s2 and for the Salm equation µ = 0.157,ξ = 1 067 m/s2.

Since in practice one should not use more than two places of decimals for the value of µ, it is suggested that µ = 0.16. For the ten avalanches of Table III the ξ values were calculated according to Salm setting µ = 0. 16 and sc = s0 These ξ values range from 728 m/s2 to 1 275 m/s2 with a mean value of 1 129.20 m/s2 and a standard deviation of 116.70 m/s2. We suggest that µ = 0.16 and ξ= 1 360 m/s2 (mean plus twice the standard deviation) be used for further calculations of the run-out distance of extreme avalanches.

Table III. VALUES OF μ AND ξ CALCULATED ACCORDING TO VOELLMY AND SALM

Let us now compare these results with the values which have been used and recommended up to date.

Reference VoellmyVoellmy (1955) states: “Little is yet known about the friction coefficient µ ” and “moreover, µ increases with the density (ρ)”. He gives the following equation (Reference VoellmyVoellmy, 1955, p. 213):

If one assumes values of ρ from 150 kg/m3 to 300 kg/m3 for extreme avalanches one obtains µs ranging from 0.08 to 0.15. With respect to ξ he states (Reference VoellmyVoellmy, 1955, p. 212): “By analogy to hydraulics, the velocity coefficient ξ for a rough stream course can be set at ξ ≈ 500 m/s2 ”, and further on (Reference VoellmyVoellmy, 1955, p. 214): “The velocity coefficient ξ varies between 400 and 600”,

In a course for avalanche zoning organized by EISLF and held in Davos from 6-8 November 1972, Sommerhalder assumed µ = 0.15 for the track section and µ = 0.20 for the run-out section of the path. However, he assumed ξ = 500 m/s2 for both sections.

In the publication Grundlagen des Lawinenverbaus Salm (1972, p. 69) writes: “For the coefficient of friction (µ) today, one assumes values from 0.15 to 0.50 depending upon the nature of the snow and the underlying ground conditions. For the roughness coefficient (ξ), one assumes a value of 400 to 600 m/s2”.

Schaerer ([1975], p. 429) assumes a µ which depends on the velocity v and he gives the relationship µ= (5 m/s)/v. According to this, µ would assume values of 0.25 to 0. 10 for velocities ranging from 20 m/s to 50 m/s. He writes that “for practical purposes, the kinetic friction may be neglected when the speed is greater than 50 m/s”. For ξ he found a value of 1 420 m/s2, and he writes (Schaerer, [1975], p. 430): “Values between 1 000 and 1 800 m/s2 with 1 400 m/s2 as an average, should be used for avalanches that move over deep, dense snow, e.g. old avalanche deposits”.

Reference Leaf and MartinelliLeaf and Martinelli (1977) in their case studies on Rocky Mountain avalanches tested the suitability of the Voellmy equation and they used the friction coefficients shown in Table IV.

De Quervain ([1977], p. 255) writes [our translation]: “For practical purposes one uses µ 0 = µp = 0.15 and µ u = 0.20 (occasionally also 0.15)”, and he continues: “it is more difficult to estimate the ξ values. Voellmy uses values of 400 to 600 m/s2. For fully developed large-flow avalanches which endanger the valley bottoms, the calculations with those values have given, to date, a satisfactory agreement with the observations. For open and smooth tracks one should assume, as a precaution, ξ = 600 m/s2”.

Table IV. Friction coefficients used by Reference Leaf and MartinelliLeaf and Martinelli (1977)

The µ values proposed and used by the above-mentioned researchers compare quite well with the value recommended in this paper. The ξ values proposed by some of them, however, agree less well with our findings. These might be changed for future calculations of maximum run-out distances.

References

Frutiger, H. 1980. Swiss avalanche hazard maps. Joumal of Glaciology, Vol. 26, No. 94, p. 518–19. [Abstract only; the full version in German is to be published in Interpraevent 1980, Bd. 3, as part of the proceedings of the symposium held at Bad Ischl, Austria, 8-12 September 1980.]CrossRefGoogle Scholar
Leaf, C. F., and Martinelli, M.,1977. Avalanche dynamics: engineering applications for land use planning. U.S. Dept. of Agriculture. Forest Service. Research Paper RM – 183.CrossRefGoogle Scholar
Martinelli, M.,1974. Snow avalanche sites: their identification and evaluation. U.S. Dept. of Agriculture. Forest Service. Agriculture Information Bulletin 360.Google Scholar
Quervain, M. R. de. [1977.] Lawinendynamik als Grundlage für die Ausscheidung von Lawinenzonen. Inter-praevent 1975, Bd. 2, p. 247–67.Google Scholar
Salm, B. 1972. Grundlagen des Lawinenverbaus. (In Castelberg, F., and others, ed. Lawinenschutz in der Schweiz. [Hrsg. von F. Castelberg, H. R. in der Gand, F. Pfister, B. Rageth, G. Bavier.] Bündnerwald. Zeitschrift des Bündnerischen Forstvereins und der SELVA, Genossenschaft der bündnerischen Holzproduzenten, Beiheft Nr. 9, p. 67–81.)Google Scholar
Salm, B. 1979. Fliessübergänge und Auslaufstrecken von Lawinen. Interner Bericht des Eidg. Institutes für Schnee-und Lawinenforschung, Nr. 566.Google Scholar
Schaerer, P. A. [1975.] Friction coefficients and speed of flowing avalanches. [Union Géeodésique et Géophysique Internationale. Association Internationale des Sciences Hydrologiques. Commission des Neiges et Glaces.] Symposium. Mécanique de la neige. Actes du colloque de Grindelwald, avril 1974, p. 425–32. (IAHS-AISH Publication No. 114.)Google Scholar
Switzerland. Bundesamt für Forstwesen. 1975. Richtlinien zur Berücksichtigung der Lawinengefahr beim Erstellen von Bauten und bei der Verkehrs-und Siedlungsplanung. Provisorische Ausgabe 1975. Bern, [Bundesamt für Forstwesen].Google Scholar
Voellmy, A. 1955. Über die Zerstörungskraft von Lawinen. Schweizerische Bauzeitung, Jahrg. 73, Ht. 12, p. 159–62; Ht. 15, p. 212–17; Ht. 17, p. 246–49; Ht. 19, p. 280–85.Google Scholar
Figure 0

Fig. 1. Longitudinal profiles of avalanche paths.

Figure 1

Table I. Avalanches showing extraordinarily long and gently sloping sections of track sf and long RUN-OUT DISTANCES so

Figure 2

Table II. Relationship between slope gradient and avalanche movement

Figure 3

Table III. VALUES OF μ AND ξ CALCULATED ACCORDING TO VOELLMY AND SALM

Figure 4

Table IV. Friction coefficients used by Leaf and Martinelli (1977)