1. Introduction
Supraglacial lakes form where meltwater collects in topographic depressions on the surface of glaciers, ice sheets and ice shelves (Reference ReynoldsReynolds, 1981; Reference Echelmeyer, Clarke and HarrisonEchelmeyer and others, 1991; Reference Lüthje, Pedersen, Reeh and GreuellLüthje and others, 2006; Reference Sundal, Shepherd, Nienow, Hanna, Palmer and HuybrechtsSundal and others, 2009; Reference Selmes, Murray and JamesSelmes and others, 2011; Reference SergienkoSergienko, 2013). These lakes are important because they lower surface albedo, increasing the absorption of incoming radiation (Reference Lüthje, Pedersen, Reeh and GreuellLüthje and others, 2006; Reference TedescoTedesco and others, 2012); they can drain to the bed of glaciers and ice sheets, influencing ice dynamics and subglacial drainage system development (Reference Van der VeenVan der Veen, 2007; Reference DasDas and others, 2008; Reference CowtonCowton and others, 2013; Reference JoughinJoughin and others, 2013); and they play a role in ice-shelf disintegration (Reference Scambos, Hulbe, Fahnestock, Domack, Burnett, Leventer, Conley, Kirby and BindschadlerScambos and others, 2003, Reference Scambos2009; Reference Banwell, MacAyeal and SergienkoBanwell and others, 2013; Reference MacAyeal and SergienkoMacAyeal and Sergienko, 2013).
Here we focus on the drainage of supraglacial lakes across the surface of ice masses, a process that changes the size and spatial distribution of lakes. Because surface-to-bed lake drainage is the only way of creating new pathways through to the bed of cold, thick ice sheets, the size and spatial distribution of lakes plays a crucial but poorly understood role in determining which parts of an ice sheet are exposed to enhanced basal sliding caused by injections of surface water to the bed.
We model the drainage of a supraglacial lake via a supraglacial channel that forms by melting due to the turbulent dissipation of heat by the water flow in the channel. Surface water can also flow through firn (Reference ForsterForster and others, 2014), as a sheet or through systems of many small channels. We focus on drainage through a single channel because observations suggest that this is a common mechanism by which lakes drain (see, e.g., Reference Tedesco, Willis, Hoffman, Banwell, Alexander and ArnoldTedesco and others, 2013) and because much of the theory needed to model this phenomenon can be borrowed from the well-developed field of open-channel hydrology (see, e.g., Reference HendersonHenderson, 1966).
Previous work has taken a similar approach (Reference Walder and CostaWalder and Costa, 1996; Reference Raymond and NolanRaymond and Nolan, 2000; Reference Mayer and SchulerMayer and Schuler, 2005; Reference Vincent, Auclair and Le MeurVincent and others, 2010). The novelty here is our more generally applicable model of channel hydrology and our detailed analysis of the physical controls on the surface drainage of supraglacial lakes on ice sheets.
Reference Walder and CostaWalder and Costa (1996) modelled lake drainage through an ice–rock breach, and Reference Raymond and NolanRaymond and Nolan (2000) adapted their model to describe surface lake drainage on alpine, debris-covered glaciers and introduce the concept of stable and unstable drainage. During stable drainage, the discharge from the lake decreases with time; during unstable drainage it increases with time. Reference Raymond and NolanRaymond and Nolan (2000) established the following criterion for unstable drainage: the initial incision rate of the channel must exceed the initial rate of lake-surface lowering. Using this criterion, they showed that a critical lake area exists above which drainage, initiated by a lake overtopping its bank, is unstable. This critical lake area was shown to depend on the temperature of the lake. Both Reference Raymond and NolanRaymond and Nolan (2000) and Reference Mayer and SchulerMayer and Schuler (2005), who used Reference Raymond and NolanRaymond and Nolan’s (2000) model to reconstruct the drainage of an ice-marginal lake in southern Greenland, assumed a constant channel width much greater than the depth of the channel water flow. Reference Vincent, Auclair and Le MeurVincent and others (2010) followed Reference Walder and CostaWalder and Costa (1996) in assuming that water flow is controlled by a transition through critical flow. All four studies simplified the calculation of flow depth, either by assuming that the flow is wide and shallow or that it is controlled by a critical flow transition.
We make neither assumption. Instead we determine the flow depth by applying Bernoulli’s equation and a force balance to water as it flows out of the lake into the channel. This allows us to apply our model to scenarios where simplifications made by previous authors are not valid, for example where low channel slope makes critical flow unlikely. However, when critical flow does occur, our model describes it with equations similar to Reference Walder and CostaWalder and Costa’s (1996). Furthermore we extend Reference Raymond and NolanRaymond and Nolan’s (2000) analysis of stable and unstable drainage, explaining the physical origin of these two styles of drainage and how and why some parameters affect stability while others do not.
Our study is motivated by several observations of surface lake drainage presented in Section 2. In Section 3 we present our model equations describing the hydraulics of water flow through a channel and the time evolution of lake depth and channel incision. In Section 4 we examine the model analytically to investigate the controls on drainage stability, and in Section 5 we present the results of numerical simulations using the model to demonstrate its behaviour and sensitivity to key parameters. In Section 6 we discuss the implications of our findings in relation to hypothesized future changes in the ablation area of the Greenland ice sheet and our new observations from East Antarctica.
2. Surface Drainage in West Greenland and East Antarctica
In this section we motivate our theoretical study with observations of well-studied large-scale lake drainage in West Greenland and similar but previously unreported drainage in East Antarctica.
Figure 1 displays two Landsat 7 satellite images acquired on 30 June 2001 and 7 July 2001 of a land-terminating section of the Greenland ice sheet south of Jakobshavn Isbræ. Figure 1c and d are enlarged images of the area outlined by the boxes in Figure 1a and b. Several blue supraglacial lakes are visible against the white ice-sheet surface. During the 7 days that separate the images the up-glacier limit of the region of the ice sheet populated by lakes moved further up-glacier and some lakes grew while others shrank or drained completely.

Fig. 1. Supraglacial lake drainage in Greenland. (a, b) Two Landsat 7 images acquired 7 days apart on 30 June and 7 July 2001. Inset in (a) shows the location of this part of the ice sheet in Greenland. Boxes in (a) and (b) indicate the region shown in more detail in (c) and (d), where the supraglacial drainage of water from one lake (B) to another (A) and the complete drainage of a third lake (C) are visible.
Water from a lake that drains completely (e.g. lake C, Fig. 1) can reach the bed (Reference DasDas and others, 2008; Reference Tedesco, Willis, Hoffman, Banwell, Alexander and ArnoldTedesco and others, 2013). Because the drainage of lakes along the ice–bed interface can affect ice dynamics (e.g. Reference DasDas and others, 2008; Reference Pimentel and FlowersPimentel and Flowers, 2011; Reference BartholomewBartholomew and others, 2011; Reference Kingslake and NgKingslake and Ng, 2013), the location and evolution of supraglacial lakes have implications for the future dynamic response of the ice sheet to atmospheric warming. Figure 1 shows that supraglacial lake water can also flow supraglacially into other lake basins (e.g. from lake B into lake A), thus redistributing potential points of basal meltwater injection.
Surface drainage is well studied in Greenland (e.g. Reference DasDas and others, 2008; Reference Selmes, Murray and JamesSelmes and others, 2011; Reference Tedesco, Willis, Hoffman, Banwell, Alexander and ArnoldTedesco and others, 2013) and the Antarctic Peninsula (e.g. Reference Sergienko and MacAyealSergienko and MacAyeal, 2005; Reference Van den BroekeVan den Broeke, 2005) but has not been widely reported for Antarctica. Figure 2 displays Moderate Resolution Imaging Spectroradiometer (MODIS) and Landsat images of the Nivlisen ice shelf, Dronning Maud Land, East Antarctica (70°68’S, 12°09’E) acquired in December 2006 (Reference Scambos, Bohlander and RaupScambos and others, 1996). Lakes form on the ice sheet’s flank near the grounding line (source lakes, Fig. 2a) before rapidly draining, spreading meltwater across the ice shelf.

Fig. 2. Surface drainage in East Antarctica. (a) MODIS optical satellite image acquired on 5 January 2008 (Reference Scambos, Bohlander and RaupScambos and others, 1996) showing source lakes, 100m surface contours (in white), the grounding line (in grey) and the Nivlisen ice shelf partially flooded with meltwater. Inset plots peak monthly mean temperatures recorded at Novolazarevskaya station during nine austral summers. (b–g) Six MODIS and Landsat images showing the time evolution of the 2007/08 flood. Red arrows indicate the flood wavefront, and the times separating the image acquisitions are shown between panels (dates are day/month/year). In (g) floodwater completely covers the previous year’s refrozen flood path. The bandings in (c), (d), (f) and (g) are artefacts introduced by a malfunction in the Landsat satellite.
Figure 2a was acquired on 5 January 2008 after several weeks of melt and drainage. The preceding temporal evolution of this drainage is shown in detail in Figure 2b–g, with the time separation between images indicated. The meltwater wavefront (red arrows) propagates across the shelf at average velocities of 1.7–6.8 m min−1 along paths created by the previous year’s refrozen floodwater. Water travels up to 70 km and floods an area of ∼260 km2 (∼3.3% of the ice shelf’s area). More images (acquired between 2002 and 2009, not displayed) show that this phenomenon occurs nearly every year. The images also reveal high interannual variability in flood extent. In austral summers beginning in 2002, 2004, 2005, 2006 and 2007 significant flooding was observed. In contrast, no flood was observed in imagery obtained during austral summer 2008/09. Meteorological observations from the Novolazarevskaya research station (Fig. 2a) show that this summer was the coolest in the study period, with monthly mean surface air temperature ≥−1 °C. Reference Trusel, Frey and DasTrusel and others’ (2012) study of Antarctic radar back-scatter, which indicates surface melting, also indicates low melt during austral summer 2008/09 in this region.
Surface drainage on Nivlisen is extensive and sensitive to temperature. The importance of ice-shelf surface lakes has been demonstrated by the disintegration of the Antarctic Peninsula ice shelves (e.g. Reference Scambos, Hulbe, Fahnestock, Domack, Burnett, Leventer, Conley, Kirby and BindschadlerScambos and others, 2003) and these new observations from East Antarctica further motivate our efforts to model and understand the surface drainage of supraglacial lakes.
3. Model Formulation
Figure 3 shows the geometry of our surface drainage model. A supraglacial lake drains through a channel incised into an ice-sheet surface, the lateral position of which does not change. We ignore the along-channel spatial dimension, assuming that the water discharge out of the lake is controlled by a single, stationary point in the channel near the lake, labelled ‘lake outlet’ in Figure 3. The following subsections derive model equations describing lake-level evolution, energy and force balances in the turbulently flowing water, critical flow and the incision of the channel.
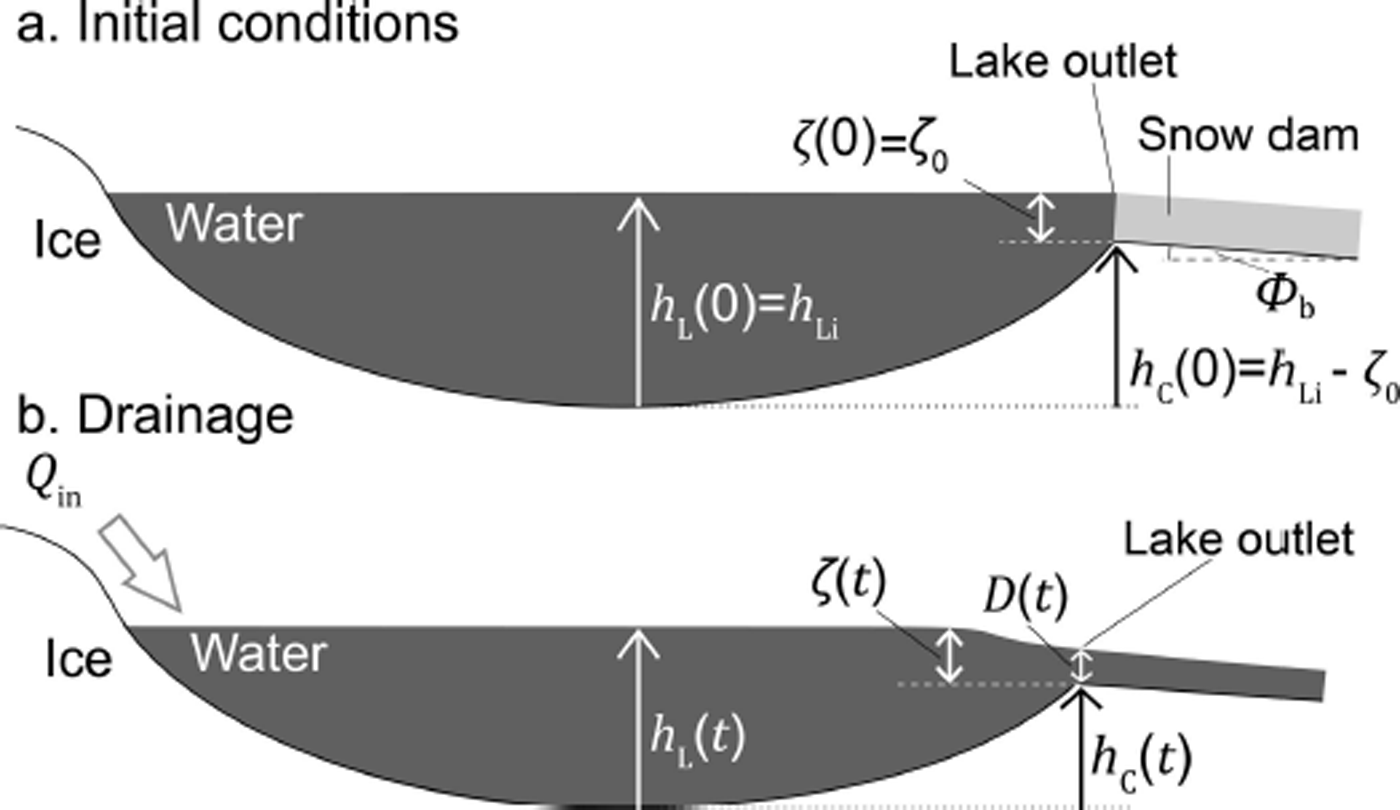
Fig. 3. Schematic of the surface lake drainage model geometry (a) before drainage (initial conditions) and (b) during drainage.
3.1. Lake evolution
The lake has volume V L, surface area A L and depth h L. These change with time and are related by the hypsometry parameterization

where A Li, V Li and h Li are the lake’s reference area, volume and depth, respectively, related by A Li = p L V Li/h Li (Reference ClarkeClarke, 1982; Reference Ng and BjörnssonNg and Björnsson, 2003). Vertically walled lakes are described by a lake-shape parameter p L = 1, bowl-shaped lakes by 1 < p L < 3, conical lakes by p L = 3 and lakes shaped like a musical horn by p L > 3 (Reference ClarkeClarke, 1982). For example, Reference KingslakeKingslake (2013, fig. 7.8) shows that the hypsometry of a supraglacial lake surveyed in Greenland by Reference Georgiou, Shepherd, McMillan and NienowGeorgiou and others (2009) can be parameterized by Eqn (1) using p L ≈ 1.5. Lake depth evolves with time t due to a meltwater input Q in (assumed constant) and outflow through the channel Q according to

This lake-level evolution equation is derived by combined water mass conservation in the lake, dV L/dt = Q in − Q, with Eqn (1) (see Reference KingslakeKingslake, 2013, ch. 2). We neglect melting of ice within the lake and its impact on lake volume and shape (Reference TedescoTedesco and others, 2012).
3.2. Bernoulli’s equation
The following derivation can be found in many open-channel hydraulics textbooks (e.g. Reference HendersonHenderson, 1966). We include the details here for completeness. We assume that all the water in the lake flows along open streamlines that extend from within the body of the lake, where we assume the water is stagnant, out along the channel. We apply Bernoulli’s equation to the water as it flows along such a streamline that lies on the water’s surface and the centre line of the channel (Reference HendersonHenderson, 1966):

where g is the acceleration due to gravity (9.8 m s−2),u is the surface velocity of the flow and z is the height of the water above an arbitrary datum, which we take as the lake bed (Fig. 3). This can be thought of as a statement of the conservation of energy in the flowing water that neglects the energy used in enlarging the channel through melt. We assume that there are no closed streamlines on the surface in the lake. We denote the surface velocity of the water in the channel at the lake outlet by v, the height of the channel bottom above the lake bed by h C and the depth of flow in the channel by D. Applying Eqn (3) at the lake end of the streamline, where u = 0 and z = h L, and in the channel at the lake outlet, where u = v and z = h C + D, yields

We assume uniform, pseudo-steady plug flow in the lake outlet, i.e. that the flow changes relatively slowly in the along-channel direction and over time and the flow velocity is uniform across the cross section of the flow. We also assume that the channel has a rectangular cross-section with constant width w. Hence, the water discharge at the lake outlet is
and Eqn (4) becomes

The solid curve in Figure 4 plots the discharge Q as a function of the depth of flow D as defined by Eqn (6). This classic curve from open-channel flow theory (e.g. Reference HendersonHenderson, 1966) has two branches with dD/dQ < 0 and dD/dQ> 0, corresponding to subcritical and supercritical flow, respectively (corresponding to Fr < 1 and Fr > 1, where the Froude number Fr is given by Fr = v(gD)−0.5). They meet at a critical point (C) where D = D C and discharge is at a maximum, Q C. Maximizing Q with respect to D by differentiating Eqn (6) reveals how D C is related to h L, h C and Q C:

Fig. 4. Depth of flow D as a function of discharge Q according to Bernoulli’s equation (Eqn (6); solid curve) and the force-balance equation (Eqn (9); dashed and dotted curves). The two force-balance curves correspond to two alternative pairs of values for the slope and hydraulic roughness of the channel.
3.3. Force balance
To complete the model’s description of water flow at the lake outlet, we balance the forces acting on a slab of water of unit along-channel length, unit width and height D. We parameterize the shear stress τ F exerted on the water by the ice with the Darcy–Weisbach equation,
where f R is the channel’s hydraulic roughness and ρ w is the density of water. The along-channel gravitational driving stress is
where φ b is the along-channel slope, which we assume constant and uniform. Again assuming steady flow, we equate τ F and τ G. Eliminating v between the result and Eqn (5) and rearranging for Q yields an expression for the discharge in terms of the channel slope, the channel width, the depth of flow and the channel roughness:

The dashed and dotted curves in Figure 4 plot this discharge–flow-depth relationship using two alternative pairs of values for the slope and hydraulic roughness of the channel. The channel corresponding to the dotted curve is steeper and smoother than that corresponding to the dashed curve. Points A and B, where these curves intercept the solid ‘Bernoulli curve’, indicate the discharge Q and depth of flow D, which obey the force-balance equation (Eqn (9)) and Bernoulli’s equation (Eqn (6)) in each channel.
3.4. Subcritical and supercritical flow
Points A and B lie on the subcritical and supercritical branches of the Bernoulli curve respectively; depending on the characteristics of the channel, flow can be subcritical or supercritical. When flow is supercritical at some position along a flow path, hydrologists usually assume that discharge is controlled by a transition from subcritical to supercritical flow somewhere upstream. At such a transition, flow is critical, and discharge and flow depth can be easily calculated by maximizing discharge with respect to flow depth (e.g. Eqn (7)).
We adopt a similar approach here to deal with supercritical flow conditions. When the solution to the Bernoulli and force-balance equations indicates supercritical flow we assume that the flow is controlled by a transition to critical flow at the lake outlet and calculate discharge with Eqn (7).
3.5. Channel incision
Heat transferred from the turbulently flowing water to the ice melts and enlarges the channel. We assume the lake temperature is 0°C, so that the only source of heat is frictional dissipation in the flowing water. The ice mass melted per unit length of the channel per unit time, m, is
(e.g. Reference Walder and CostaWalder and Costa, 1996), where L is the specific latent heat of fusion of ice (334 kJ kg−1). For simplicity we assume that melting occurs in the channel bottom but not at the sides. This is motivated by other studies that make the same simplification (e.g. Reference Mayer and SchulerMayer and Schuler, 2005; Reference Vincent, Auclair and Le MeurVincent and others, 2010) and the fact that at present it is unclear how best to apportion frictional melting between the channel’s bottom and sides. Accordingly, the rate of change of the height of the channel bottom above the lake bed is given by
Equations (2), (5), (6), (7), (10) and (12) complete the model. They describe respectively the time evolution of lake level, the relationship between discharge and flow velocity, Bernoulli’s equation in the water flowing from the lake into the channel, the characteristics of critical flow, the balance of the frictional and gravitational forces in the flowing water, and the rate of channel incision.
The model assumes that (1) drainage is controlled entirely by the flow through one point in the channel near the lake, labelled ‘lake outlet’ in Figure 3; (2) flow at the lake outlet can be assumed to be steady and uniform, i.e. the flow changes relatively slowly in time and along the channel; (3) we can ignore the energy used in melting when considering the balance of potential and kinetic energy in the water as it flows out of the lake into the lake outlet; (4) melt is restricted to and distributed evenly across the floor of the channel such that the channel’s width and slope are constant; and (5) energy dissipated as heat by the water flowing through the lake outlet is used locally for melting.
These assumptions are restrictive but analysis of the model still yields useful mechanistic insights into drainage.
4. Drainage Stability
We will demonstrate how supraglacial drainage of a lake can be either stable or unstable. As shown by Reference Raymond and NolanRaymond and Nolan (2000), the origin of the two styles of drainage is the competition between the channel incision rate and the lake lowering rate. We take the analysis further and show how stable drainage remains bounded and may stop before the lake has emptied completely, while unstable drainage grows unboundedly with time, completely emptying the lake. We also explain why some model parameters affect drainage stability while others do not, and analyse the drainage of three idealized lakes: (1) a vertically sided lake that receives no input of water (p L = 1, Q in = 0), (2) a non-vertically sided lake that also receives no input (p L > 1, Q in = 0), and (3) a vertically sided lake that receives a constant water input (p L = 1, Q in > 0). We restrict this section’s analyses to considering subcritical flow conditions and show later in a numerical sensitivity analysis that this is appropriate for a wide range of realistic parameter values.
We define ζ as the height difference between the lake’s surface and the bottom of the channel (ζ = h L − h C) (Fig. 3) and begin by deriving an expression for the time evolution of ζ. Recasting the Bernoulli and force–balance equations (Eqns (6) and (10)) in terms of the flow velocity v (using Eqn (5)) and rearranging both for the flow depth D yields

and

Eliminating D between the two equations above and rearranging yields the following expression relating the flow velocity and the height difference ζ:

Eliminating v between this and the channel-incision equation (Eqn (12)) yields
where

Using Q = vwD, Eqn (14) is expressed as

Then eliminating v between this expression and Eqn (15) reveals how discharge Q depends on ζ:
where

Substituting this into Eqn (2) yields

The model has been reduced to a pair of ordinary differential equations for h L and h C (Eqns (16) and (21)). An expression for the time evolution of ζ is obtained by differencing dh L /dt and dh C /dt to give

This equation incorporates the two competing mechanisms that control lake drainage: changes in the lake level due to an imbalance between the meltwater input Q in and the discharge through the channel (the first term on the right) and downward incision of the channel into the ice surface through frictional melting (the second term on the right). Armed with this equation, the equation for the time evolution of h C,
and the definitions of α and β,

we consider three idealized lakes, chosen to simplify the analysis and allow us to demonstrate the physics of channelized supraglacial drainage as described by our model.
The first idealized lake receives no water input from its surroundings and is vertically sided (Section 4.1). We will show that such a lake can drain stably, with discharge decreasing with time, or unstably, with discharge increasing with time. Applying the model to such a simplified lake allows the physical controls on its behaviour to be analysed, but it is probably not representative of real supraglacial lakes. The second idealized scenario we analyse is drainage from a lake with hypsometry such that its surface area decreases during drainage. We show that when such drainage is initially unstable it stabilizes after the surface area has decreased sufficiently. Finally, a vertically sided lake is supplied with an input of water, which we show always causes the lake to empty completely.
4.1. A vertically sided lake with no input
For a vertically sided lake (p L =1) that receives no water input (Q in = 0), Eqn (22) reduces to

4.1.1. The drainage stability parameter
Consider the initiation of lake drainage shown in Figure 3. A snow dam in the channel fails when the lake is a height ζ 0 above the channel bottom (ζ = ζ 0) and lake drainage begins; this initiation mechanism has been observed in Greenland (Reference Tedesco, Willis, Hoffman, Banwell, Alexander and ArnoldTedesco and others, 2013). Equation (25) determines how ζ changes with time as drainage progresses. Of particular significance is the quantity in parentheses in Eqn (25), the sign of which determines whether ζ increases or decreases with time. We call this quantity the ‘drainage stability parameter’,
If Λ is positive, dζ/dt is also positive and ζ increases unstably with time. Physically, the channel incises the ice surface more rapidly than the lake’s surface is drawn down by the water flowing out through the channel. A positive feedback operates between ζ and ∂ζ/∂t because discharge Q increases with ζ (Eqn (19)). Discharge grows unboundedly with time, so we call this drainage unstable. Vertically sided lakes that drain unstably will always empty completely. In contrast, if Λ is negative, ζ and Q always decrease with time. Physically, the lake’s surface, which is initially higher than the channel (by a distance ζ 0), is drawn down more rapidly than the channel is incised, which causes the depth of flow to decrease over time. Note that, if Λ is negative but sufficiently close to zero, the lake can still empty before the decreasing Q has had time to reach zero (this will be shown in Section 4.1.3). This style of drainage, which does not grow unboundedly with time, we call stable.
The importance of the stability parameter Λ can be seen more directly after integrating Eqn (25) to yield expressions for the time evolution of the height difference ζ and, using Eqn (19), the discharge Q:


When Λ > 0, the terms in the denominators on the right of Eqns (27) and (28) decrease with time, causing ζ and Q to ‘blow up’ in finite time ![]() ; of course, the lake runs out of water before this. Conversely, when Λ < 0, ζ and Q decrease with time, and drainage can halt before all the water has been evacuated from the lake. Figure 5 depicts these two drainage styles and shows the time evolution of discharge as defined by Eqn (28) for several different values of Λ.
; of course, the lake runs out of water before this. Conversely, when Λ < 0, ζ and Q decrease with time, and drainage can halt before all the water has been evacuated from the lake. Figure 5 depicts these two drainage styles and shows the time evolution of discharge as defined by Eqn (28) for several different values of Λ.

Fig. 5. Time evolution of channel discharge corresponding to six values of the drainage stability parameter Λ calculated using Eqn (32). The six stability parameters have been calculated using the initial lake areas, A Li, shown and the following typical values for other parameters: f R = 0.25, w C = 2 m, φ b = 0.01 and p L = 1.
4.1.2. Physical controls on stability
Clearly, how much and how rapidly water escapes from the lake during drainage depends strongly on the stability of drainage. We now examine what controls stability, with the aim of understanding how the physical conditions on an ice sheet’s surface could affect water transfer between supra-glacial lakes.
From Eqn (26), the stability parameter Λ depends on the reference surface area A Li. In fact, in plotting Figure 5 we used A Li to vary Λ. (Note that, because we are considering a vertically sided lake, lake area A L equals its reference value A Li always, but more generally A Li is the initial lake area.) Equation (26) shows that increasing A Li encourages unstable drainage. Physically, this is because, for a given outflow, the channel incision rate is independent of the lake’s surface area (Eqn (23)), whereas, the larger the lake’s area is, the slower its level drops. Because the rates of lake-surface drawdown and channel incision compete to control the outlet flow depth and hence how discharge evolves, a larger lake area encourages unstable drainage.
To understand the other physical controls on drainage stability, we use the definitions of α and β (Eqn (24)) to expand Λ (Eqn (26)):

Increasing the channel slope φ b increases the water flow velocity, which increases channel-incision and lake-drawdown rates. This manifests as an increase in the quantity outside the square brackets in Eqn (29) and increases the rate at which discharge Q changes with time (Q increases or decreases with time, depending on drainage stability). However, for the lake-drawdown rate this increase is slightly compensated for by a decrease in flow depth caused by the increase in φ b and the hydraulics of open-channel flow (as described here by the Darcy–Weisbach equation). This effect manifests as a decrease in the second term in the square brackets. Hence the net effect of increasing φ b is to promote unstable drainage.
In contrast, increasing the channel width w promotes stable drainage. The channel-incision rate is independent of w, but increasing w accelerates lake drawdown by increasing the discharge through the channel for a given flow velocity (Eqn (5)), stabilizing drainage.
Interestingly, the hydraulic roughness f R is absent from the square brackets in Eqn (33) and hence does not affect drainage stability. Decreasing f R increases the flow velocity, which affects both channel incision and lake drawdown. Decreasing f R decreases flow depth, compensating for the increase in discharge from the faster-flowing water. However, this is balanced by a corresponding decrease in channel-incision rate due to a decrease in the shear stress τ b (Eqn (8)) and hence a drop in the heat dissipation that incises the channel.
Note that the height of the snow dam when it fails, ζ 0 (the initial value of ζ) does not appear in the definition of Λ (Eqn (29)) and so it has no effect on drainage stability. It does, however, affect the initial discharge and hence how fast the lake empties and, during stable drainage, whether it empties at all.
Table 1 summarizes the effects that increases in the initial lake area A Li, the channel slope φ b, the channel width w, the channel roughness f R and the intial flow depth in the channel ζ 0 have on the lake-level drawdown rate, the channel-incision rate and drainage stability.
Table 1. Summary of the impact of varying key model parameters on lake-surface drawdown rate, channel incision rate and drainage stability

4.1.3. Stable but complete drainage
During stable drainage (Λ < 0) the discharge decreases to zero asymptotically with time. Drainage may end (ζ → 0) before the lake is empty; alternatively, the lake may empty completely before ζ reaches zero. To understand these alternatives, we use the expressions for dh C /dt and dζ/dt in Eqns (23) and (25) to examine how model solutions move through h C−ζ phase space.
Figure 6 plots several solution trajectories in the h C−ζ phase space, each corresponding to a different value of Λ. Examples of both stable (Λ < 0) and unstable (Λ > 0) trajectories are plotted. Their gradients are determined by dividing Eqn (23) by Eqn (25) to give


Fig. 6. Model trajectories in h C−ζ phase space corresponding to five different values for the drainage stability parameter Λ. The critical stability parameter ΛC is defined in Eqn (36). The lake is vertically sided (p L = 1).
This equation and Figure 6 show that, during stable drainage, dh C/dζ > 0, and whether or not the lake empties completely is determined by the magnitude of this gradient. When dh C/dζ is sufficiently small, the solution trajectory in Figure 6 meets the vertical axis (where ζ = 0) and drainage halts while there is still water in the lake. When dh C/dζ is large, the trajectory meets the horizontal axis (where h C = 0) and the lake empties.
As the channel bottom height is initially h Li−ζ 0 (Fig. 3), Eqn (30) and Figure 6 show that its final height, h final, is given by
The lake will empty completely if h final = 0. The critical value of Λ just sufficient to empty the lake as both discharge and ζ reach zero, ΛC, is given by

A stability parameter Λ which obeys ΛC ≤ Λ ≤ 0 will result in stable but complete drainage.
4.2. A non-vertically sided lake with no water input
Real supraglacial lakes are not vertically sided. Usually, the fuller a lake is, the larger its area is (Fig. 3), with a hypsometry parameter p L > 1. We examine the drainage of such lakes here. Still ignoring water input to the lake (Q in = 0), with p L ≠ 1, Eqn (22) becomes

or
where

is a generalized stability parameter (it reduces to Λ when p
L = 1). This parameter accounts for the effect of the lake’s decreasing area as it drains, given instantaneously by ![]() . How does the new hypsometry affect lake stability? Initially the lake depth is equal to its reference value h
Li, so
. How does the new hypsometry affect lake stability? Initially the lake depth is equal to its reference value h
Li, so ![]() ; whether a lake is initially stable or unstable does not depend on its shape. However, as the lake drains, h
L decreases, so the lake area decreases, reducing
; whether a lake is initially stable or unstable does not depend on its shape. However, as the lake drains, h
L decreases, so the lake area decreases, reducing ![]() . Before the lake empties,
. Before the lake empties, ![]() will always drop below zero because h
L appears in the denominator of the second term on the right of Eqn (35). When this happens drainage will stabilize. This stabilization can halt drainage altogether or, if it occurs when h
C is already close to zero, merely slow the final stages of drainage. These two possibilities are illustrated in Figure 7, which sketches how model trajectories in h
C−ζ phase space depend on the lake-shape parameter p
L. Trajectories were calculated by forward Euler time stepping of Eqns (23) and (33) using values of model parameters that lead to initially unstable drainage and – except the shape parameter p
L – do not change between calculations. Note that because we use the same A
Li and h
Li for each calculation but vary p
L, we are implicitly adjusting V
Li between calculations in order to compare lakes with the same initial area but different shapes.
will always drop below zero because h
L appears in the denominator of the second term on the right of Eqn (35). When this happens drainage will stabilize. This stabilization can halt drainage altogether or, if it occurs when h
C is already close to zero, merely slow the final stages of drainage. These two possibilities are illustrated in Figure 7, which sketches how model trajectories in h
C−ζ phase space depend on the lake-shape parameter p
L. Trajectories were calculated by forward Euler time stepping of Eqns (23) and (33) using values of model parameters that lead to initially unstable drainage and – except the shape parameter p
L – do not change between calculations. Note that because we use the same A
Li and h
Li for each calculation but vary p
L, we are implicitly adjusting V
Li between calculations in order to compare lakes with the same initial area but different shapes.

Fig. 7. Model trajectories in h
C−ζ phase space corresponding to 11 different equally spaced values of the lake-shape parameters p
L between 1 and 3. In all cases initially the lake-stability parameter ![]() . The rightmost curve corresponds to p
L = 1 and the other curves correspond to progressively larger values of p
L. The trajectories corresponding to the three highest p
L values intercept the h
C axis, so drainage is halted before the lake empties.
. The rightmost curve corresponds to p
L = 1 and the other curves correspond to progressively larger values of p
L. The trajectories corresponding to the three highest p
L values intercept the h
C axis, so drainage is halted before the lake empties.
When p L > 1, trajectories are deflected from the straight trajectory corresponding to p L = 1. This deflection increases with time during each simulation and with p L when comparing between simulations. If p L is sufficiently high, drainage is halted before the channel bottom is incised to the lake bed.
Physically, the lake area decreases as the lake depth decreases, so the lake-drawdown rate for a given discharge is increased without any corresponding change in the channel incision rate. This stabilizes drainage by allowing the lake drawdown to ‘catch up’ with channel incision. This effect is enhanced for more ‘horn-shaped’ lakes with higher p L values.
4.3. A vertically sided lake with a water input
We now return to the vertically sided lake (p L = 1) and consider what happens if it receives water from its surroundings (Q in > 0). In this scenario, Eqn (22) becomes
We now demonstrate how this equation shows that, unlike in the case Q in = 0, drainage cannot cease before the lake empties. Suppose that Λ > 0. In this case the right-hand side of Eqn (36) is always positive, so drainage is unstable, discharge increases unboundedly with time and the lake empties completely. Suppose now that Λ < 0. If |Λζ 3/2| > |Q in /A Li|, ζ decreases because dζ/dt < 0 (Eqn (36)). Alternatively, if |Λζ 3/2| < |Q in /A Li|, ζ increases because dζ/dt > 0 (Eqn (36)). Hence when Λ < 0, ζ relaxes towards a positive value (−Q in/A LiΛ)2/3. The input to the lake maintains the lake’s surface height above the channel bottom’s height, so stable drainage and channel incision continues until the lake empties completely.
To understand this stable but complete drainage we compare the discharge corresponding to a depth of flow ζ = (−Q in/A LiΛ)2/3 with the input to the lake Q in. From Eqn (19),
so the discharge after ζ has reached (−Q in/A LiΛ)2/3 is
From the definition of Λ (Eqn (26)), this becomes

When Λ < 0, αA Li/β < 1, and hence 0 < (1 – αA Li/β) < 1. So, from Eqn (39), Q > Q in and the lake drains. Furthermore, the rate of lake-surface drawdown is dh L /dt = (Q in − Q)/A Li, or, using Eqn (39),

The higher the input to the lake, the faster it drains because a higher input maintains a deeper flow in the channel that causes more rapid incision. This analytical result only holds for stable drainage, when the discharge has relaxed to (−Q in/A LiΛ)2/3. Numerical sensitivity analysis of the model (Reference KingslakeKingslake, 2013), more extensive than that reported in the next section, suggests that this result also applies during unstable drainage.
4.4. Summary
In our model, supraglacial drainage from a vertically sided surface lake that receives no water input (p L =1, Q in = 0) evolves in one of three ways depending on the stability parameter Λ. When Λ < −α/(h Li/ζ 0 − 1), lake drainage is stable (i.e. lake level is drawn down faster than the channel is incised) and halts when water remains in the lake. When −α/(h Li/ζ 0 − 1) ≤ Λ ≤ 0, drainage is still stable but results in the complete emptying of the lake. And when Λ > 0, drainage is unstable and discharge increases unstably with time because the channel is incised faster than lake level is drawn down. Increasing lake area, increasing channel slope and decreasing channel width all promote unstable drainage. The hydraulic roughness of the channel does not affect drainage stability, but it does affect the magnitude of Λ and hence the rate at which discharge changes with time.
The drainage of more realistically shaped lakes with p L > 1 is governed by the same physics except that, as drainage progresses, a modified stability parameter, which takes account of the lake’s shape, decreases and stabilizes drainage. This can halt drainage before the lake empties.
When a lake is supplied with water by its surroundings, it may drain stably or unstably but it always drains completely. The larger the water supply the faster the lake empties.
5. Numerical Simulations
We now solve the full model numerically, taking into account the possibility of critical flow at the lake outlet, first to demonstrate the drainage scenarios examined in the previous section and second to perform a numerical sensitivity analysis. Characteristics of the model revealed by the numerical analysis that could not be examined analytically in the previous section include the areas of parameter space that cause critical flow, the unstable but incomplete drainage caused by very slow increases in discharge and how areas of model parameter space corresponding to unstable and stable drainage compare with observations of lakes in Greenland.
We numerically step the lake depth and the channel-bottom height forward in time by solving Eqns (12) and (16) with the Euler method. At each time step, we determine if flow is subcritical or supercritical by evaluating whether the force-balance curve (dashed and dotted curves, Fig. 4) intercepts the line D = D C (the horizontal solid line, Fig. 4) to the left or right of point C. If flow is supercritical we calculate the depth of flow and discharge in the lake outlet using Eqn (7). Alternatively, if flow is subcritical we determine these quantities by solving the Bernoulli and force-balance equations (Eqns (6) and (10)) simultaneously using the Newton–Raphson method.
Simulations start with a full lake (h L = h Li) and terminate when the lake has emptied (h L ≤ 0) or discharge becomes very low (Q ≤ 0.002 m3 s−1).Again we assume that drainage begins by the mechanical failure of a dam of water-saturated snow in the channel. This initial condition is implemented by starting the simulation with the level of the bottom of the channel a distance ζ 0 below the lake surface elevation (Fig. 3a).
5.1. Simulating stable and unstable drainage
We present the results of four simulations numbered 1–4. Simulations 1 and 2 use vertically sided lakes with no input and demonstrate stable and unstable drainage, respectively. Simulation 3 shows how a vertically sided lake drains stably and empties completely when it is supplied with an input of water, and simulation 4 shows how initially unstable drainage can stabilize and halt before the lake empties when the lake is not vertically sided.
We use a typical value for the reference lake depth h Li =10 m (Reference Georgiou, Shepherd, McMillan and NienowGeorgiou and others, 2009) and estimate an appropriate hydraulic roughness coefficient from published data. Reference Mernild, Hasholt and ListonMernild and others (2006) calculated Manning roughness coefficients, n′, between 0.036 and 0.058 m−1/3 s in supraglacial streams, with an average value of 0.050 m−1/3 s. The roughness coefficient f R is related to n′ by f R = 8gn′2/R H 1/3 (Reference ClarkeClarke, 2003, his eqn 24), where the hydraulic radius R H is the ratio of the flow’s cross-sectional area and wetted perimeter. Hence, we use f R = 0.25 in our simulations.
Figure 8 shows lake discharge hydrographs and time series of lake level and channel-bottom height from simulations 1 and 2. Both simulations assume a vertically sided lake (p L = 1) that receives no water input (Q in = 0) and drains through a 2 m wide channel (w C = 2). Drainage initiates when a 1 m high snow dam fails (ζ 0 = 1 m). The left-hand panels (Fig. 8a and c) display results from simulation 1, which uses a lake area of 1 km2 and a channel slope of 0.01, and the right-hand panels (Fig. 8b and d) plot results from simulation 2, which uses a larger lake area of 3 km2 and a larger channel slope of 0.03.

Fig. 8. Numerical model simulations demonstrating stable and unstable drainage. The top panels (a, b) plot hydrographs and the bottom panels (c, d) plot lake-level and channel-height time series, from simulations using two vertically sided lakes with different surface areas and channel slopes. The left-hand plots (a, c; simulation 1) show results for a small lake (A Li = 1 km2) with a gently sloping channel (φ b = 0.01). The right-hand plots (b, d; simulation 2) show results for a larger lake (A Li =3 km2) with a steeper channel (φ b = 0.03). The small lake drains stably and the large lake drains unstably. Both simulations use Q in = 0 m3 s−1, w C = 2 m, ζ 0 = 1 m and f R = 0.25.
The smaller lake drains stably and the larger lake drains unstably. The discharge from the smaller lake (simulation 1) is initially 2.8 m3 s−1 and decreases with time throughout the simulation (Fig. 8a). As Λ < ΛC (from Eqns (26) and (32)), Λ = −2.4 × 10−6 m−1/2 s−1 and ΛC = −5.1 × 10−8 m−1/2 s−1), the lake level drops faster than the channel incises (Fig. 8c) and after 100 days the lake level has dropped <1 m and the simulation stops when Q = 0.002 m3 s−1. Discharge from the larger lake (simulation 2) is initially 3.4 m3 s−1 and increases throughout the simulation (Fig. 8b). As Λ = 5.3 × 10−7 m−1/2 s−1, the channel incises faster than the lake level drops (Fig. 8d). After 22 days the channel has reached the lake bed and the lake will soon empty completely.
Figure 9 shows lake-level and channel-height time series and discharge hydrographs from simulations 3 and 4, which use the same initial lake area and channel slope as simulations 1 and 2, respectively.

Fig. 9. Numerical model simulations demonstrating how drainage evolution is affected by meltwater input to the lake (Q in > 0) and a lake whose surface area decreases as it drains (p L > 1). The left-hand plots (a, c; simulation 3) show results for a small lake (A Li = 1 km2) with a gently sloping channel (φ b = 0.01) that receives a water input Q in = 5 m3 s−1.The right-hand plots (b, d; simulation 4) show results for a larger lake (A Li = 3 km2) with a steeper channel (φ b = 0.03) whose surface area decreases with depth, p L = 3. Both simulations use w = 2 m, ζ 0 = 1 m and f R = 0.25.
In simulation 3 the smaller lake is supplied with a water input Q in = 5 m3 s−1.This causes the channel discharge Q to approach a value greater than Q in (∼5.97 m3 s−1,Eqn (38)) and the lake drains stably and completely.
In simulation 4 the shape of the larger lake is altered so that its surface area decreases as it drains (p
L = 3). Figure 9b and d show the results. For the first 11 days, discharge increases. It then peaks and begins to fall. This stabilization occurs at the moment the modified stability parameter ![]() drops below zero. The decreasing lake surface area accelerates lake drawdown, allowing the lake level to catch up with channel incision. Drainage ends after ∼40 days (Fig. 9d).
drops below zero. The decreasing lake surface area accelerates lake drawdown, allowing the lake level to catch up with channel incision. Drainage ends after ∼40 days (Fig. 9d).
5.2. Numerical stability sensitivity analysis
To complete the numerical investigation of the model, we explore its sensitivity to three physical parameters: the initial lake area A Li, the channel slope φ b and the height, ζ 0, at which the snow dam in the channel fails. These were chosen as interesting parameters to consider because A Li and φ b may vary systematically across ice sheets and we are interested in emphasizing, as predicted by the analysis in Section 4, that drainage stability is independent of ζ 0. We refer the reader to Reference KingslakeKingslake (2013) for a more extensive exploration of these and other parameter sensitivities using the same model.
We conduct multiple year-long model simulations while varying A Li, φ b and ζ 0 systematically between simulations, and after each simulation we record the final depth of the lake, h final, and, if the lake empties completely, the time taken for this to occur, T E.
Between 2005 and 2009, Reference Selmes, Murray and JamesSelmes and others (2011) observed mean and maximum Greenland lake areas of 0.8 and 17 km2, so to bracket these observations we vary A Li between 0.05 and 30 km2. Similarly we vary φ b between 0.005 and 0.1 and ζ 0 between 0.1 and 3 m to encompass realistic ranges for these parameters. Note that one might expect lower channel slopes on ice shelves. All simulations use Q in = 0 m3 s−1, w C = 2 m and p L = 1.
Figure 10 shows how h final and T E vary with A Li, φ b and ζ 0. Each row of plots corresponds to a set of simulations where two of the parameters are varied and the third is kept constant. Two regions of parameter space are evident, one where h final > 0 m and T E is not defined, corresponding to incomplete drainage, and another where h final =0 m and 13 ≤ T E ≤ 365 days, corresponding to complete drainage.

Fig. 10. The results of exploring the model’s sensitivity to the initial lake area A Li, the channel slope φ b and the height at which the snow dam in the channel fails, ζ 0. Filled contour maps show how final lake depth (a, c, e; left column) and the time taken to empty the lake (b, d, f; right column) vary with these parameters. In all simulations Q in = 0 m3 s−1, w C = 2 m and p L = 1. Solid green lines separate regions corresponding to stable and unstable drainage (plotted using Eqn (29) with Λ = 0). Green dotted and dashed lines in (a–d) indicate the mean and maximum areas of lakes reported by Reference Selmes, Murray and JamesSelmes and others (2011). Crosses indicate locations in each parameter space of simulations 1 and 2 (Fig. 8).
The results show, as predicted in Section 4, that increasing A Li and φ b decreases the stability of drainage. Also, ζ 0 does not affect drainage stability, but it does increase the rate at which a lake drains, and decreases the amount of water left in the lake after stable drainage has halted before the lake is completely empty.
Also plotted in each panel in Figure 10 are solid green curves evaluated using Eqn (29) with Λ = 0, which separate regions of stable and unstable drainage. These critical-parameter curves and the boundaries between incomplete and complete drainage (visible as the edges of the regions where T E is not defined in Fig. 10b, d and f) are approximately aligned; stable drainage often leads to incomplete drainage. However, in one small region of parameter space adjacent to the critical-parameter curves (e.g. Fig. 10f), drainage is stable but complete. This style of drainage was discussed in Section 4.1. It occurs when the stability parameter Λ is negative but close to zero (more precisely when −α/(h Li /ζ 0 − 1) ≤ Λ ≤ 0).
Conversely, in another region adjacent to the critical parameter curves (e.g. Fig. 10d), drainage is unstable but results in incomplete drainage. This was not discussed above. It is an artefact of the finite length of simulations (1 year). In these simulations discharge increases very slowly with time because Λ is small and positive. Hence, after one model year the lake is not completely empty.
The lake areas observed by Reference Selmes, Murray and JamesSelmes and others (2011) bracket our modelled boundaries between stable and unstable drainage (Fig. 10). For example, according to our model with this choice of parameters, a lake whose area is A Li = 0.8 km2, the mean area observed by Reference Selmes, Murray and JamesSelmes and others (2011), will drain stably regardless of φ b, whereas a lake whose area is their largest observed (A Li =17 km2) would drain unstably through a channel with φ b > 0.003.
The boundary of the region in parameter space corresponding to simulations that involve critical flow is visible in Figure 10a, b and f as a kink in the otherwise smooth contours at φ b ≈ 0.032. For a wide range of channel slopes our model simulates subcritical flow. When φ b > 0.032, flow is critical and drainage does not depend on φ b. This is expected, as the equations that describe critical flow (Eqn (7)) do not involve φ b.
6. Discussion
Using a simple model we have examined how the surface drainage of a supraglacial lake evolves after it initiates in a pre-existing channel. This evolution can be stable or unstable and depends on a competition between drawdown of the lake’s surface and channel incision. Drainage instability increases with the lake’s area and the channel’s slope, and decreases with the channel’s width. Lake hypsometry also affects stability, with lakes whose surface area decreases during drainage promoting stability. Drainage stability is not affected by the channel’s hydraulic roughness, the lake’s initial depth or the height of the snow dam in the channel, the failure of which initiates drainage. Irrespective of whether a lake that receives a water input from its surroundings drains stably or unstably, it will always empty completely. We have shown analytically that, in the stable case, a higher input causes a higher lake discharge. Reference Kingslake and NgKingslake’s (2013) numerical sensitivity analysis suggests that this increase in discharge with lake input also occurs in the unstable case.
Previous authors (Reference Walder and CostaWalder and Costa, 1996; Reference Vincent, Auclair and Le MeurVincent and others, 2010) have simplified the determination of flow depth in channels draining lakes by assuming critical flow at the lake outlet. In contrast, our numerical sensitivity analysis suggests that subcritical conditions dominate for a wide range of parameter values and our analytical examination of the model considered only subcritical flow. This examination could be repeated for the critical flow regime, which may be dominant in some situations. As critical flow is independent of the channel slope and the hydraulic roughness, some aspects of our analysis related to these parameters will be irrelevant. However, key processes, such as the competition between lake level and channel incision, and the influence of parameters such as lake area, lake input and channel width, will be qualitatively similar.
Field observations (e.g. Reference Mayer and SchulerMayer and Schuler, 2005; Reference Tedesco, Willis, Hoffman, Banwell, Alexander and ArnoldTedesco and others, 2013) and remote-sensing surveys (e.g. Reference Selmes, Murray and JamesSelmes and others, 2011; Reference Johansson, Jansson and BrownJohansson and others, 2013) of lakes and lake-drainage events could be used to test our model and constrain its parameters (e.g. channel hydraulic roughness f R). However, several model limitations need to be considered.
The model ignores along-channel spatial variations and the lake water’s sensible heat. Developing the model to include along-channel variation could reveal dynamics associated with a melt–slope–discharge feedback that could operate along channels. The lake’s sensible heat will affect the lake’s shape and contribute to channel incision; its inclusion in the model may be necessary to simulate drainage realistically (Reference TedescoTedesco and others, 2012).
We have assumed a constant channel width. Although previous work (e.g. Reference Mayer and SchulerMayer and Schuler, 2005; Reference Vincent, Auclair and Le MeurVincent and others, 2010) justified this assumption with observations of deep, vertical-walled supraglacial channels, it may be invalid when this width is less than the flow depth and a physical explanation for these observations is presently lacking. A potentially related consideration is the mechanism by which drainage initiates. In our model we initiate drainage by snow-dam failure. An alternative mechanism is the overtopping of the lake’s basin in the absence of a preexisting channel. After initial sheet flow, a feedback between melt and flow depth would form a channel. Two-dimensional modelling of this process may help us understand how it influences channel width and how drainage evolves after it is initiated in this way.
We have also assumed that the lake drains through a single channel. Our approach could be applied to drainage through two or more channels. In such an extension the discharge through N identical channels would be N times the drainage through an isolated channel. However, because channels are unlikely to be identical, some will grow more rapidly than others. The discharge through these channels may increase at the expense of the discharge through the more slowly growing channels, until all the lake outflow is concentrated in one channel. This feedback mechanism may explain why lakes are often observed to drain through one large channel (e.g. Figs 1 and 2).
The model assumes that the only mechanism affecting the elevation of the channel bottom is frictional melting by the flowing water. In reality, ice flow – both the large-scale flow of the ice sheet through the lake basin and small-scale flow induced by the presence of the channel – may also contribute. Upward flow of the ice sheet as it leaves the lake basin will tend to raise the bottom of the channel (Reference Darnell, Amundson, Cathles and MacAyealDarnell and others, 2013), and small-scale flow around the channel will raise the channel bottom and decrease channel width (Reference Jarosch and GudmundssonJarosch and Gudmundsson, 2012). We ignored these potentially complex dynamics, but they may be crucial for multi-year channel evolution (Reference Darnell, Amundson, Cathles and MacAyealDarnell and others, 2013) and the formation of englacial drainage systems from surface channels (Reference Jarosch and GudmundssonJarosch and Gudmundsson, 2012).
Despite limitations of our model, our results have implications for our understanding of the Greenland ice sheet. A concern among glaciologists is that atmospheric warming could increase the area of the ice sheet populated by supraglacial lakes, resulting in a corresponding increase in the area of the bed that receives injections of meltwater from the surface. This would affect ice dynamics (Reference Lüthje, Pedersen, Reeh and GreuellLüthje and others, 2006; Reference BartholomewBartholomew and others, 2011). It is this coupling between surface melt and ice dynamics that the mechanisms highlighted by our analysis may influence.
Reference Lüthje, Pedersen, Reeh and GreuellLüthje and others (2006) suggested that lakes will tend to be larger as the area of the ice sheet populated by lakes expands inland because of lower mean ice-surface slopes higher on the ice sheet. In terms of the surface drainage simulated by our model, such a shift in elevation corresponds to movement through the model’s parameter space. Specifically, an increase in mean lake area increases the propensity of lakes to drain unstably, enhancing the relocation of surface water to lower elevations and limiting the availability of meltwater for injection to the bed. However, lower average surface gradients higher on the ice sheet imply lower channel slopes, which have the opposite effect according to our theory. Alternatively, lake area and channel slope may both be controlled by large-scale surface roughness, itself dependent on basal topography, local surface processes and ice-flow dynamics. How other factors such as lake shape, channel width and lake input may change under atmospheric warming scenarios is also currently unclear.
Surface drainage not only relocates water, but also directly throttles the drainage of lake water to the bed of ice sheets and reduces an ice sheet’s dynamic response to lake drainage. Reference Tedesco, Willis, Hoffman, Banwell, Alexander and ArnoldTedesco and others (2013) report field observations of a supraglacial lake draining relatively slowly to the bed of the Greenland ice sheet by delivering water over the ice sheet’s surface via a surface channel to a nearby moulin. They measured the ice sheet’s dynamic response to this event and to another, more rapid drainage event, which included no surface drainage. During the more rapid event, water was delivered directly from the lake bottom to the bed of the ice sheet via hydrofracture and the creation of new moulins. The ice sheet’s dynamic response to the slower event that included surface drainage was less than half of its response to the more rapid event. Our model could be used in future work to examine the coupling between lake drainage and ice dynamics in scenarios such as this where surface drainage plays a crucial role.
Our new observations of extensive surface drainage in East Antarctica (Fig. 2) allow speculation on mechanisms affecting drainage stability in this system. The most rapid drainage appears to originate from several of the largest lakes positioned near the grounding line on the ice-sheet flank, where the surface slope is greatest. This is consistent with our theory.
How other important factors such as lake shape, channel slope and lake input evolve over time in this system may depend on whether lakes are advected with ice flow or form in topographic depressions created by ice dynamics and remain geographically stationary, as they do in Greenland. For example, if lake-bed ablation decreases with increasing water depth, an advected lake’s walls will steepen as shallower areas preferentially ablate. This corresponds to a decrease in the lake-shape parameter p L and the stability of drainage. Furthermore, as a lake is advected with ice flow, local ice surface slope and the lake’s catchment may increase over time. This would also decrease the stability of drainage.
Lakes may be formed in the blue-ice area (to the lower right of Fig. 2a) and advected towards the grounding line over many years, becoming increasingly unstable until input is sufficient to cause the rapid drainage we observe.
Regardless of whether lakes are advected with ice flow, variation in lake input will affect the timing and rate of lake drainage through the mechanisms highlighted by our modelling. This may help to explain the interannual variability seen in drainage extent and will be investigated in future work.
7. Conclusions
We have developed a model of the surface drainage of supraglacial lakes. The model yields qualitative results that highlight and physically explain important and previously unrecognized controls on ice-sheet surface hydrology. Lakes are more prone to drain unstably, which often empties them completely, when initial lake area, lake input and channel slope are larger. Also, when lakes are supplied with an input of water they always drain completely and do so faster when supplied with a larger input. We have discussed these findings in relation to the well-studied supraglacial drainage system in the ablation area of the Greenland ice sheet and previously unreported surface lake-drainage phenomena in East Antarctica. Future work will focus on improving the model and applying it quantitatively to these systems to understand their variability and predict their future.
Acknowledgements
J. Kingslake acknowledges the support of a University of Sheffield PhD studentship and the British Antarctic Survey Polar Science for Planet Earth programme. Meteorological data from Novolazarevskaya station, Nivlisen, were obtained from the Russian Federation NADC, Arctic and Antarctic Research Institute (AARI), www.aari.nw.ru/projects/Antarctic/data/Catalogue.html (last accessed on 17 October 2014). We thank Bernd Kulessa, Ian Willis and three anonymous reviewers for useful comments that improved the paper.















