Introduction
The mass balances of the Greenland and Antarctic ice sheets are of interest because of their complex linkage to climate variability and their direct effects on sea-level change. In recent decades, the spatial distribution of mass input and output data has greatly improved as field observations have been complemented by advances in remote sensing and dynamic modeling. Approximately 399Gt a–1 of ice is accumulated on the Greenland ice sheet above the equilibrium line, and approximately 1637 Gt a–1 on the Antarctic ice sheet (modified from Reference Giovinetto and ZwallyGiovinetto and Zwally, 2000; Reference Zwally and GiovinettoZwally and Giovinetto, 2001), which is equivalent to the removal of 5.6 mm a–1 from the oceans. The net mass balance is the difference between the mass input in the zone of net accumulation and the sum of the net ablation at the surface (including runoff), the direct discharge of ice into the ocean, and discharge of subglacial water across the grounding line. Uncertainties in previous mass-balance estimates (± 53.0Gt a–1 for Greenland and ± 384Gt a–1 for Antarctica (Reference HuybrechtsHuybrechts and others, 2001)) have been largely due to the difficulty of accurately measuring all the mass input and output fluxes (e.g. Reference Rignot and ThomasRignot and Thomas, 2002).
Expected responses of the ice sheets to climate warming are both growth in thickness of the inland ice areas, due to increasing precipitation, and thinning near the margins, due to increasing surface melting (Reference Huybrechts, Kuhn, Lambeck, Nhuan, Qin, Woodworth and HoughtonHuybrechts and others, 2001). In addition, dynamic ice thinning near the margins may be induced by processes such as removal or thinning of adjacent ice shelves or ice tongues (Reference ThomasThomas, 2003; Reference Rignot, Casassa, Gogineni, Krabill, Rivera and ThomasRignot and others, 2004; Reference Scambos, Bohlander, Shuman and SkvarcaScambos and others, 2004) as well as enhanced basal sliding due to surface meltwater reaching the ice–bedrock interface (Reference Zwally and LiZwally and others, 2002c). Reference AlleyAlley and others (2003) reviewed the state of knowledge of ice- sheet behavior from recent observational and modeling advances and suggested that the ice sheets may have a greater sensitivity to climate warming than previously considered.
Since the first results using altimeter surveys of ice-sheet elevation changes to estimate changes in ice volume and mass balance (Reference ZwallyZwally, 1989), there has been an increasing use of altimetric measurements of elevation change (dH/dt) to improve upon estimates from mass-flux studies. Recent results include the detection of significant thinning of the margins of the Greenland ice sheet, which was attributed to increases in both melting and dynamic thinning (Reference AbdalatiAbdalati and others, 2001; Reference KrabillKrabill and others, 2004), thickening of the EA ice sheet, attributed to increases in precipitation (Reference Davis, Li, McConnell, Frey and HannaDavis and others, 2005), and growth of the interior of Greenland (Reference Johannessen, Khvorostovsky, Miles and BobylevJohannessen and others, 2005). Nevertheless, a comprehensive assessment of the current mass balance of the ice sheets has not been made, due in part to the limited performances of satellite radar altimeters over the steeper ice-sheet margins and in part to limitations in the spatial and temporal coverage of airborne laser-altimeter surveys. Elevation changes are also caused by temporal variations in the rate of firn compaction (Reference ZwallyZwally, 1989; Reference BraithwaiteBraithwaite, 1994; Reference Arthern and WinghamArthern and Wingham, 1998; Reference Zwally and LiZwally and Li, 2002), but corrections for this effect have not previously been made.
In this study, we extend the analysis of radar altimeter data from the two European Remote-sensing Satellites (ERS- 1 and -2) to 90.0% of the Greenland ice sheet, 77.1% of the Antarctic ice sheet and 81.8% of the Antarctic ice shelves. In Greenland, we use results of Airborne Topographic Mapper (ATM) laser-altimeter surveys to increase coverage of the margins. We also use optimal-interpolation procedures to provide nearly complete spatial coverage of the ice sheets and shelves (Figs 1a and 2a). For the first time, we use a firn compaction model with a 20 year record of satellite-based surface temperatures to calculate corrections for elevation changes due to changes in the rate of firn compaction caused by temporal variations in firn temperature and nearsurface melting.

Fig. 1. Greenland. (a) Distribution of surface elevation change data by source, derived from ERS-1 and -2 radar altimetry, ATM (closest- neighbor interpolation from airborne surveys), and obtained by optimal interpolation: ice terminus of coterminous ice sheet (red), equilibrium line (black dashes), 2000 m elevation contour (blue), drainage divides (black), drainage system designation (number in circles), and location of H(t) series depicted in Figure 3a (labeled blue full circles). (b) Distribution of elevation change (dH/dt). (c) Distribution of ice- thickness change (dI/dt).

Fig. 2. Antarctica. (a) Distribution of surface elevation change data by source, derived from ERS-1 and -2 radar altimetry and obtained by optimal interpolation: coast and grounding line (black, heavy), ice-shelf front (black dashes), drainage divides (black, thin) of which the wider trace depicts the WA/EA divide by ice provenance, drainage system designation (number in circles), and location of H(t) series depicted in Figure 3b (labeled blue full circles). Excluded from this study: whole area of system 25, grounded-ice area in 26, and grounded- and floating-ice areas in 27. (b) Distribution of elevation change (dH/dt). (c) Distribution of ice-thickness change (dI/dt).
Observed and Interpolated Elevation Changes (dH/dt)
Measurements of ice surface elevations (H) from ERS-1 and -2 radar altimeters are compiled as elevation time series, H(t), from which elevation change (dH/dt) values are derived (Fig. 3). The ERS altimeters operated in either ocean mode with a resolution of 45 cm per range gate or ice mode with a resolution of 182 cm per range gate. We use only ice mode data, because of a spatially variant bias between the modes and the greater spatial and temporal coverage of the ice mode data. We applied our V4 range-retracking algorithm, atmospheric range corrections, instrument corrections, slope corrections and an adjustment for solid tides (Reference Zwally, Brenner, Fu and CazanaveZwally and Brenner, 2001). Instrument corrections include subtraction of a 40.9 cm bias from ERS-1 elevations to account for a different instrument parameter used for ERS-2 (Reference FemeniasFemenias, 1996) and corrections for drifts in the ultra-stable oscillator and bias changes in the scanning point target response that are obtained from the European Space Agency. We use the DUT DGM-E04 orbits, which have a radial orbit precision of 5–6cm (Reference Scharroo and VisserScharroo and Visser, 1998).

Fig. 3. H(t) series (black) and multi-parameter linear–sinusoidal function (red), labeled same as locations shown in Figures 1a and 2a and listing site elevation in meters, and derived dH/dt± σs in cm a–1. Crossovers within 100 km circle of location are used except within 50 km for PG2. (a) Greenland: CW (central west), 3087, +13.5 ± 1.6; SW (southwest), 2456, +12.0 ± 1.7; CE (central east), 2700, +8.4 ± 0.5; NC (north central), 2314, +5.2 ± 0.5; NS (near Summit), 3225, +3.0± 0.8; JI (Jakobshavn Isbræ), 1316, –7.4 ± 5.4; SE (southeast), 2173, –12.7 ± 1.7; HG (Humboldt Glacier), 472, –30.6 ± 8.8; NM (north margin), 1365, –30.7 ± 5.1; NI (‘Northeast Greenland Ice Stream’), 614, –42.2 ± 6.2. (b) Antarctica: AP (Antarctic Peninsula), 1832, +35.7 ± 3.9; UK (upper Kamb Ice Stream), 941, +25.9 ± 1.1; CI (Carlson Inlet), 271, +23.0 ± 2.5; AX (Alexander Island), 688, +21.2 ± 3.0; AI (Amery Ice Shelf), 49, +15.0 ± 1.7; WR (western Ross Ice Shelf), 52, +8.6 ± 0.6; WC (West Antarctica – coastal), 1734, +6.8 ± 1.3; RI (Ronne Ice Shelf), 54, +5.3 ± 2.7; VL (Victoria Land), 2297, +5.3 ± 1.1; DM (Dronning Maud Land), 3104, +3.9 ± 0.7; BY (Byrd Station), 1524, –1.2 ± 0.7; GM (Gamburtsev Mountains), 3074, –4.1 ± 0.7; MI (MacAyeal Ice Stream), 682, –7.2 ± 1.1; CR (central Ross Ice Shelf), 52, –9.4 ± 1.2; UL (upper Lambert Glacier), 1068, –11.4 ± 1.3; SH (Shirase Glacier), 1160, –11.6 ±3.8; LC (Larsen C ice shelf), 42, –17.9 ± 1.8; LB (Larsen B ice shelf), 28, –20.4 ± 2.0; DG (Denman Glacier), 1161, –20.6 ± 5.0; GI (George VI Ice Shelf), 51, –21.0 ± 1.6; WI (Wilkins Ice Shelf), 27, –24.5 ± 2.7; WG (west Getz Ice Shelf), 45, –27.6±2.0; TF (Thwaites Glacier Tongue), 40, –31.4 ± 2.9; PF (Pine Island Glacier Tongue), 68, –35.3 ± 2.3; TG (Thwaites Glacier), 774, –42.2 ±3.0; EG (east Getz Ice Shelf), 93, –42.4±2.6; TN (Totten Glacier), 866, –44.8±4.8; SF (Smith Glacier Tongue), 52, –60.5 ± 3.2; PG2 (Pine Island Glacier), 627, –68.9 ± 3.4; PG (Pine Island Glacier), 323, –87.9 ± 5.7; SG (Smith Glacier), 407, –261.8 ± 7.5 (for this site only, note factor of 3).
The time periods are from mid-April 1992 to mid-October 2002 for Greenland and to mid-April 2001 for Antarctica. The series are constructed for gridpoints nominally 50km apart from sets of elevation differences measured at orbital crossovers using time periods of 91 days. Our methods enable us to obtain useful H(t) series over more of the ice- sheet area than some other analyses have. For most gridpoints, crossovers within a 100 km circle centered on the gridpoint are used, and within 200 km for a few points. Crossover selection is also limited to elevations within ±250 m of the elevation at the gridpoint center, which for slopes >1/200 restricts the selected areas to bands along elevation contours where the elevation changes tend to be spatially coherent. The first sequence of elevation differences at crossings between period T1 and all successive T¡ is combined with the second sequence of those for crossings between T 2 and all successive Tix and so forth for all additional sequences, which are then combined in one H(t) (Reference Zwally, Brenner, Fu and CazanaveZwally and Brenner, 2001). The resulting H(t) series use all independent crossovers, including inter-satellite crossovers, which greatly increases the number of crossovers and the accuracy of the results (more crossovers and longer time intervals), as compared to using only the first sequence or only intra-satellite crossovers. For Greenland, we have 16 x 106 crossovers from ERS-1/ERS-1, 52 × 106 from ERS-2/ERS-2, and 59 × 106 from ERS-1/ERS-2. For Antarctica, we have 157 × 106 crossovers from ERS-1/ERS-1,276 × 106 from ERS-2/ERS-2, and 419 × 106 from ERS-1/ERS-2, whereas only crossovers from ERS-1/ERS-1 and ERS-2/ERS-2 are used by Reference Davis, Li, McConnell, Frey and HannaDavis and others (2005).
We obtain dH/dt values for 602 (90%) of the 670 gridpoints on Greenland ice and 4085 (79%) of the 5175 gridpoints on Antarctic ice, i.e. 77% of the grounded points and 82% of the floating points (Table 1). The distance between points in our nominal 50km grid, which is mapped in a polar stereographic projection with plane tangent at the pole, ranges between 48.784 km at 60° and 52.286 km at 90°. In Greenland, the coterminous ice-sheet area is sampled by 670 gridpoints, excluding islands and ice caps not attached by ice (Fig. 1b). The area of Antarctica is sampled by 5238 gridpoints, excluding islands not attached by ice (Fig. 2b). The working grid is reduced to N = 5175 by excluding the relatively small areas of grounded ice in Graham Land and grounded and floating ice in eastern Palmer Land, for which it is not possible to assemble reliable H(t) series. Of the 5175 gridpoints used, 4606 are on grounded ice (coterminous ice sheet, islands attached by ice, and ice rises) and 569 are on floating ice (ice shelves and ice tongues). East Antarctica (EA) and West Antarctica (WA) are divided on the basis of ice provenance (Fig. 2) rather than the traditional boundary along the Transantarctic Mountains (Reference Zwally, Beckley, Brenner and GiovinettoZwally and others, 2002b).
Table 1. Mean values and errors of terms (dH/dt, dC/dt, dB/dt, dS/dt) used in the estimate of ice-thickness change (dI/dt) for areas of Greenland and West and East Antarctica defined by ice provenance, listing net mass balance (dF/dt, dM/dt) and sea-level contribution (SLE). All values are listed as computed to allow tracing of estimates in other columns (some second and third decimals are not significant); small differences are due to use of round-off values

Although the ERS-1 and -2 altimeters are nearly identical, a significant inter-satellite elevation bias was measured over the ice sheets during the 13 months of simultaneous operation from May 1995 through May 1996. The ERS-1/ERS-2 bias does not occur over the oceans nor on some of the flat ice surfaces. Although the bias tends to be correlated with each of three interrelated parameters (received back- scatter power, surface slope and surface elevation), it was not possible to formulate the bias as a consistent function of these parameters over all of the ice sheet and ice shelves. Therefore, for Antarctica, we averaged the measured biases at crossovers between ERS-1 and ERS-2 on a 50 km grid and smoothed the averages over five gridpoints with a linear weighting with distance from the center. For Greenland, we averaged the crossover differences on a 50 km grid using crossovers within 400 km and a restriction to elevations within ±250 m of the gridpoint, giving a smoothing similar to that for Antarctica.
The applied bias correction lowers the ERS-2 elevations by an average of 30.7 cm with standard deviation (SD) = 20.9 cm spatial variation over Greenland, by 17.5 cm with SD = 13.3 cm over Antarctic grounded ice, and by 12.0 cm with SD = 9.6cm over Antarctic floating ice. Over Greenland, the bias correction lowers the average dH/dt by roughly 3.5cm a–1. Over Antarctica, the correction lowers the average dH/dt by 2.4cm a–1 with SD = 1.7cm a–1 on grounded ice and by 1.6cm a–1 with SD = 1.2 cm a–1 on floating ice. The effects of the bias correction on calculations of mass change (dM/dt) for the ERS gridpoints are roughly –50Gt a–1 for Greenland and –205Gt a–1 for Antarctica, indicating the importance of this correction. For Greenland, Reference Johannessen, Khvorostovsky, Miles and BobylevJohannessen and others (2005) used a different method to calculate the bias, and state ‘the calculated spatially averaged ERS-1/ERS-2 bias is 21.5 ± 2.0 cm’, which may be smaller than our 30.7cm because we include more lower- elevation gridpoints. They also state the effect on dH/dt varies from typically ~2 cm a–1 over the interior plateau to about 20 cm a–1 over the ... margins (presumably negative values), which spans our average –3.5cma–1. Reference Davis, Li, McConnell, Frey and HannaDavis and others (2005) in effect apply a bias correction by calculating separate H(t) series for ERS-1 and ERS-2 and adjusting them together during the 12 month overlap period, but do not state the magnitude of their adjustments.
Another significant correction is applied for the dependence of the height measured by the altimeter on the received backscatter power similar to those applied in preceding studies (Reference Wingham, Ridout, Scharroo, Arthern and ShumWingham and others, 1998; Reference Davis, Li, McConnell, Frey and HannaDavis and others, 2005). We derive a spatially variant sensitivity (dH/dG) of the measured height (H) to changes in the measured back- scattered power using the value of the automatic gain control (AGC) as the measure of the backscattered power (G). We first construct G(t) time series at each gridpoint using the same procedure as for the H(t) series. For each gridpoint, we correlate the N values of H i (t i ) and G i (t i ) and calculate a linear fit, H = H0 + (dH/dG)G and the correlation coefficient (R). The corrected elevation series is then Hci = Hi – (dH/dG)(G i, –G 0), where G 0 = –H 0(dH/dG –1. The sensitivity factor (dH/dG) of the elevation to the backscatter is correlated with R, so for smaller values of R the magnitudes of the sensitivity and the correction decrease. Where the absolute value of R is <0.2, no backscatter correction is applied, because the correlation and sensitivity are both small. Where dH/dG<–0.2 m dB –1, it is limited to –0.2 m dB –1, and where dH/dG>0.7 mdB–1 it is limited to 0.7 mdB–1 to limit a few outlying values with poorer statistics.
The average effect of the backscatter correction on dH/dt is small, but local corrections can be large. For example, at Byrd Station (80°S, 120°W), the dH/dG is 0.40 m dB–1, R is 0. 90, and the range of G variation is 3.2 dB with a strong seasonal cycle. The uncorrected dH/dt is 5.4 ± 1.3 cm a–1 with a seasonal amplitude of 64cm peak-to-peak, and the corrected dH/dt is –1.2 ± 0.7 cm a–1 with a smaller seasonal amplitude of 24 cm. Generally, the backscatter correction appears to remove noise and significantly improve the regularity of the seasonal cycle. In Greenland, the mean correction applied to dH/dt is only –0.02 cm a–1 with a 2.36 cm a–1 SD spatial variation. In Antarctica, the mean correction is –0.34 cm a–1 with a 2.94 cm a–1 SD spatial variation on grounded ice and –0.13 cm a–1 with a 2.52 cm a–1 SD spatial variation on floating ice. The approximate effects on calculations of mass change (dM/dt) for the ERS gridpoints are –1.5 Gt a–1 for Greenland and –32Gta–1 for Antarctica.
A multi-parameter linear–sinusoidal function is fitted to the H(t) series to obtain linear trends of dH/dt, while accounting for seasonal variations in the elevation measurement (Fig. 3). The frequency of the sine function is fixed at 1 year. The fit calculates the slope (dH/dt), intercept, phase (e.g. the date of minimum) and the amplitude of the seasonal cycle with standard deviations of each parameter. In most H(t) series, the linear–sinusoidal model represents the data very well. The standard deviation (σ s) of the linear slope (dH/dt) obtained from the multi-parameter fitting is used as the estimate of the error in the derived dH/dt trends. The σs are affected by departures of the slope from the model representation of a linear trend and a seasonal sinusoidal variation, as well as by the measurement errors in H i(t i). Such departures may include unmodeled temporal variability due to short-term variability of the accumulation rate or other factors. Therefore, the σs provide estimates of the errors that include effects of natural variability in the elevation, which we carry through to estimates of the mass balance. Alternatively, Reference Davis, Li, McConnell, Frey and HannaDavis and others (2005) use an ‘autoregression’ technique (Reference Ferguson, Davis and CavanaughFerguson and others, 2004) to match non-linear variations of the seasonal cycle and interannual variability, which in general tends to reduce the σs of the linear term. We believe it is more appropriate for the unmodeled variability to be represented in σs, giving a larger error estimate. Also, removing interannual variability can lead to a linear trend that does not accurately represent the change during the period of the measurements. Maps of our σs, including an optimal interpolation of σs with a factor that increases with the distance of interpolation, are shown in the Appendix (Fig. 7).
The dH/dt at Byrd Station (BY in Figs 2a and 3b), for example, is –1.2 ± 0.7 cm a–1, which is comparable to a global positioning system-based measurement (Reference Hamilton, Whillans and MorganHamilton and others, 1998) of –0.4 ± 2.2 cm a–1 within the range of errors. Adjusting our dH/dt for firn-compaction (dC/dt = –0.7 cm a–1) and bedrock motion (dB/dt = +1.7 cm a–1) gives an ice thinning rate of 2.2 cm a–1, which compares well with the thinning rate of 3 cm a–1 from field measurements of ice flow and mass-continuity calculations (Reference WhillansWhillans, 1977). In contrast, a region about 175 km to the southwest and inland of Kamb Ice Stream has large elevation increases (e.g. dH/dt = +25.9 ± 1.1 cm a–1 at point UK in Figs 2a and 3b).
The distributions of dH/dt are shown in Figures 1b and 2b, and descriptive statistics are listed in Table 1. We utilize ATM results (Reference AbdalatiAbdalati and others, 2001) from 1993 to 1999 and closest-neighbor interpolation to obtain dH/dt values for an additional 3% of the area of Greenland. We use the optimal interpolation method of kriging with default options in the Golden Software Inc. Surfer® (version 7.0) computer program to provide nearly complete spatial coverage (100% of the coterminous grounded-ice area of Greenland and 99% of each of the grounded- and floating-ice areas of Antarctica). The grounded and floating areas of Antarctica are interpolated separately and merged. Most of the interpolated points are widely distributed over the steeper coastal areas of the ice sheets, except for the area of Antarctica south of 81.5° S (Fig. 2a and b). The observed dH/dt along the 81.5° S perimeter of the interpolated area are mostly small (i.e. –5 to +5 cm a–1), except for the region of large increases south of point UK in WA. The average dH/dt on grounded ice in the area south of 81.5°S is +1.6 cm a–1, and the calculated average ice thickness and mass changes are relatively small (d//dt = +0.64 cm a–1 and dM/dt = +14Gta–1).
Calculation of Ice-Thickness changes (dI/dt)
Deriving ice-thickness changes (dI/dt) from dH/dt values requires correction for elevation changes (dC/dt) induced by temporal variations in the rate of firn compaction, and adjustment for vertical motion of the underlying bedrock (dB/dt) or sea level (dS/dt). Over grounded ice, the thickness change is
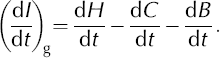
We use the radial components (dB/dt) of three models of isostatic rebound (from Reference Ivins, Wu, Raymond, Yoder, James and SiderisIvins and others, 2001; Reference HuybrechtsHuybrechts, 2002; Reference PeltierPeltier, 2004), labeled (dB/dt)I,H,P respectively, interpolated to our gridpoints. The model of Reference Ivins, Wu, Raymond, Yoder, James and SiderisIvins and others (2001) is global and covers Greenland, although the referenced work is limited to Antarctica. The averages (Fig. 8 in Appendix) are weighted to account for distributions that showed similar patterns, i.e. for Greenland dB/dt = 1/4(dB/dt)P+1/4(dB/dt)H + 1/2(dB/dt)I, and for Antarctica dB/dt = 1/4(dB/dt)I +1/4(dB/dt)P+1/2(dB/dt)H. The dB/dt errors are estimated at ±1/2 of the range from the average of the two results with similar patterns to the third model result.
On floating ice, the change in thickness is
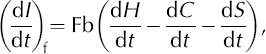
where Fb is the freeboard ratio of total thickness to freeboard height (ice surface elevation above sea level). The Fb value for each gridpoint is determined from buoyancy using Fb = ρ w/(ρ w-ρ if), where ρ w = 1028.5 kgm–3 is the density of Antarctic Shelf Water (Reference Whitworth, Orsi, Kim, Nowlin, Jacobs and WeissWhitworth and others, 1998) and ρ if is the mean density of the floating-ice column. We iteratively calculate ice thickness and ρ if values for each gridpoint to account for the dependence of ρ if on thickness. The resulting mean ice thickness of the Antarctic ice shelves (N = 569) is 488 m (SD = 313 m), the mean ρ if is 870 kg m–3 (SD = 28kgm–3) and the mean Fb is 6.62 (SD = 0.89). We use dS/dt = 2.8 ± 0.4 mm a–1 for contemporaneous sea-level rise (Reference Leuliette, Nerem and MitchumLeuliette and others, 2004).
The dC/dt values (Fig. 9 in Appendix) are calculated for each gridpoint with an enhanced firn compaction model that is sensitive to variations in firn temperature and surface melting, obtained from a 20 year record of surface temperatures from satellite infrared observations. The firn compaction model (Reference Li and ZwallyLi and Zwally, 2002; Reference Zwally and LiZwally and Li, 2002) is augmented by inclusion of the effects of vapor transport in the firn (Reference Li and ZwallyLi and Zwally, 2004) and the effects of near-surface melting. The model uses a temperature- dependent activation energy and has greater sensitivity and a more rapid compaction response to variations in temperature than other models (e.g. Reference Arthern and WinghamArthern and Wingham, 1998). The model produces seasonal variations in the rate of densification, seasonal variations in density with depth, and seasonal changes in surface elevation that are generally consistent with observations (Reference Li and ZwallyLi and Zwally, 2002, Reference Zwally, Beckley, Brenner and Giovinetto2004; Reference Zwally and LiZwally and Li, 2002; Reference Li, Zwally, Cornejo and YiLi and others, 2003; Reference Dibb and FahnestockDibb and Fahnestock, 2004). Surface melting and refreezing is included by using an empirical melting–temperature model (Reference Braithwaite and ZhangBraithwaite and Zhang, 2000), which gives melting when the monthly average temperature is >–8°C, and the corresponding changes in density are calculated. A similar treatment of the effect of melting on densification is given in Reference Reeh, Fisher, Koerner and ClausenReeh and others (in press). The mean accumulation rates are held constant with time in the model, since the intent is to calculate temperature-dependent variations in surface elevation and not variations caused by variability in accumulation rates, which are discussed in the next section.
The model is driven with the latest available data of monthly surface temperatures (Reference ComisoComiso, 2003; Reference Comiso and ParkinsonComiso and Parkinson, 2004) for 1982–2003 from satellite-borne Advanced Very High Resolution Radiometers. The temperature data for the Greenland ice sheet have been improved from the early version of the dataset by a recalibration using more ground-station data of surface temperature. A steady- state 1 year monthly temperature cycle determined as the average of the first 3 years (1982–84) of temperature data, with constant accumulation (A) and surface firn density of 0. 3, is used to establish the initial steady-state density profile with depth. The surface height variation C(t) is calculated from 1982 to 2003 and dC/dt is obtained by a linear fit to the C(t) for the time period of the H(t) and derived dH/dt. We use an error estimate of ±30% on the calculated dC/dt, which is approximately equivalent to the range of error that would be induced by ±25% errors in the temperature anomalies.
In general, warmer temperatures increase the rate of compaction and lower the surface elevation, whereas colder temperatures raise the surface elevation. Near-surface melting and subsequent refreezing in the firn also lowers the surface by changing firn to higher-density ice, which in turn affects the rate of subsequent densification. Although much of the densification in the upper firn layers occurs during the warmer summer months, temperature anomalies in winter also have a large impact on the rate of densification during summer, because of their preconditioning effect on the summer firn temperatures.
In Greenland, the calculated dC/dt values are mostly negative, showing primarily the effect of a positive trend in winter temperatures as well as the increase in summer melting during the 1990s. The average dC/dt over the accumulation zone is –1.71 cma–1, indicating an average surface lowering from an increased rate of compaction. Without adjustment for dC/dt, this surface lowering might be incorrectly interpreted as a mass loss of 23.4 Gta–1 (using an average column ice density of 0.9). In WA, the average dC/dt for grounded ice is –1.58 cm a–1 (28.4 Gta–1 equivalent) and on the floating ice is –2.79 cma–1 (130Gta–1 equivalent). These surface lowerings in WA are caused by a regional warming trend, including melting effects on the ice shelves and in some coastal areas. In EA, the average dC/dt on the grounded ice is +0.21 cm a–1 (–19.3Gta–1 equivalent), with the largest increases around 135° E within a few hundred km of the coast. The small increase in EA is due to the small cooling trend over much of the region. On the floating ice in EA, the average dC/dt is –1.70cma–1 (73.2 Gta–1 equivalent), which is due to warming and melting of the ice shelves indicated by the temperature record.
Our calculated dI/dt for Greenland and Antarctic subregions are listed in Table 1 and shown in Figures 1c and 2c. The data are weighted for small differences in the area of the grid squares in the polar stereographic map projection. Values for each drainage system (DS) are listed in Table 2 and shown in Figure 4a.

Fig. 4. Distribution of mean dI/dt (a) and dM/dt (b) for drainage systems of Greenland, West Antarctica and East Antarctica (EA includes data for DS1g&f, and DS26f).
Table 2. Mean values and errors in the estimate of ice-thickness change (dI/dt) and net mass balance (dF/dt, dM/dt) for grounded-ice (g) and floating-ice (f) areas of drainage systems (DS) in Greenland, West Antarctica and East Antarctica, listing sea-level contribution (SLE) and the ratio of net mass balance to adjusted net accumulation at the surface (Aii) for each. All values are listed as computed to allow tracing of estimates in other columns (some second and third decimals are not significant); small differences are due to use of round-off values

Estimation of Mass Changes (dM/dt)
The mass change (dM/dt) associated with dI/dt depends on whether the change in thickness of the firn/ice column is caused by the ice dynamics not being in balance with the long-term (multi-decadal) accumulation rate or is caused by shorter-term (decadal) variability in accumulation rate (A(t)). Separating components of dI/dt gives
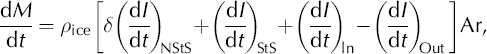
where ρ ice = 0.917 is the density of ice (i.e. relative to water) and Ar is the area of the firn/ice column. In the first term, (dI/dt)NStS is the change in thickness due to any nonsteady-state (NStS) change in firn thickness from short-term changes in A(t) and/or temperature (T(t)). The factor S can range from about 0.33 to 1 if the rate of firn compaction is not in steady state with the surface mass input. The term ρ iceδ may be considered as the effective density of the NStS component of the mass change. In steady state the velocity of firn compaction is constant, the density profile with depth is not changing and the flux of lower-density firn input at the surface is equal to the downward flux of ice at depth (δ = 1 and (dI/dt)NStS = 0). In the ablation zone, the first term is zero, neglecting the seasonal effect of winter snow cover. The second term in Equation (3) is due to the steady-state (StS) component of the mass added at the surface, and ρ ice(dI/dt)StS is equal to the long-term average accumulation rate (A). The third and fourth terms are due to the average horizontal ice flow into and out of the column during the measurement period, which may include short- as well as long-term dynamic changes. The sum of the last three terms determines the long-term mass balance.
In general, δ is a function of the time histories of A(t) and T(t) and the response time τ t of the firn compaction process, which is on the order of a few years to decades. Our calculations of dC/dt remove the effect of T(t) for 10 years prior to and including the measurement period. However, because current knowledge of A(t) is limited, the S(dI/dt)NStS term cannot be completely determined. Fortunately, several factors reduce the effect of variations of A(t). First, short-term stochastic fluctuations in A cause both positive and negative δ(dI/dt)NStS and therefore tend to average out in a 10 year period. However, such fluctuations appropriately increase our estimated error (σs) for dH/dt, an example of which is discussed below for an apparently non-linear H(t). Second, in integrals of dM/dt over large regions, some of the δ(dI/dt)NStS are likely to be positive and some negative, thereby also reducing their net effect. Therefore, we use the approximation
where ρ a is the average density of the firn/ice column, i.e. 0. 90 on grounded ice and 0.87 on floating ice, and dI/dt is the observed thickness change. We show dM/dt for Greenland and Antarctic sub-regions and drainage systems in Tables 1 and 2 and Figure 4b and discuss the results in the next section. for Greenland and Antarctic sub-regions and drainage systems in Tables 1 and 2 and Figure 4b and discuss the results in the next section.
Our approximation is equivalent to assuming the dI/dt are distributed throughout the firn/ice column, and that NStS firn compaction terms are on average small compared to the longer-term balance terms. As improved information on A(t) is acquired (e.g. Reference BoxBox and others, in press; Reference Monaghan, Bromwich and WangMonaghan and others, in press) the effect on densification can be calculated and δ(dI/dt)NStS estimated. Meanwhile, we note that changes in A(t) tend to be positively correlated with T(t), with data and models showing correlations ranging from about 5 to 20% per kelvin (e.g. Reference ZwallyZwally, 1989, n. 26; Reference Kapsner, Alley, Shuman, Anandakrishnan and GrootesKapsner and others, 1995). Therefore, where A(t) is correlated with T(t), our approximation will estimate greater mass gain or less mass loss than is actually occurring in regions that are warming, and less mass gain or greater mass loss than is actually occurring in regions that are cooling. The magnitude of this effect depends on the timescale of the variations in A(t). As noted, sub-decadal variations tend to average out in a 10 year observation. Decadal trends during only the measurement period would have the most impact, while decadal trends that are part of a longer-term trend would have small impact because the non-steady-state densification term would be small.
Alternatively, choosing a smaller value of ρ a would further reduce our estimates of overall mass imbalance, which are shown to be small. To increase our estimates of mass imbalance, or to change their sign, would require selective application of δ values regionally and/or assumptions regarding the relative magnitude of the dynamic vs sur-face-balance terms in Equation (3). Previously, a commonly used pa, implicitly or explicitly, was the 0.92 density of ice (e.g. Reference KrabillKrabill and others, 2000). Reference ZwallyZwally (1989) used 0.5 and 0.92 to give a range of mass estimates. Reference Davis, Li, McConnell, Frey and HannaDavis and others (2005) used ρ a = 0.35 to estimate dM/dt based on a positive dH/dt in EA. However, the surface density is close to 0.3 in most locations, and 0.35 is the typical density of the top annual layer or two. Therefore, using 0.35 is equivalent to assuming that a positive dH/dt is continuously caused solely by the addition of new firn, with little subsequent compaction from year to year, and that the long-term mass-balance terms (accumulation plus dynamic) in Equation (3) are zero. In that case, Equation (3) would be

where all thickness changes are assumed to be caused by short-term changes in accumulation and F is the change in mass of the firn. To illustrate the effect of this assumption on estimates of the overall mass-balance values, in Tables 1 and 2 we also list dF/dt values using δ = 0.44 or ρ a = 0.4, which is a typical mean density for the top strata corres-ponding to 10 years of accumulation as shown by wide-spread sampling of the ice sheets (e.g. Reference BensonBenson, 1962; Reference Kojima and MellorKojima, 1964). The dF/dt calculations include the dC/dt correction for temperature effects on firn compaction.
Finally, we note that our dM/dt estimates for the ice shelves include mass changes caused by thickening or thinning, which may be affected by changes in the rate of discharge of grounded ice into the shelves. However, the estimates do not take into account mass changes resulting from possible systematic changes in the ice-shelf fronts due to episodic calving events (e.g. Reference Zwally, Beckley, Brenner and GiovinettoZwally and others, 2002b) or ice-shelf disintegration (e.g. Reference Skvarca, Rack, Rott and DonángeloSkvarca and others, 1999).
Discussion of Regional changes in Elevation, Thickness and Mass
In Greenland, most dH/dt values on the inland ice sheet above 2000m are increasing in the range 0–15 cma–1 (Fig. 1b), with an average of 4.77±0.14cma–1 (Table 1). For example, dH/dt for four inland locations at central west (CW: 13.5±1.6cm a–1), southwest (SW: 12.0±1.7cma–1), central east (CE: 8.4±0.5cma–1) and north central (NC: 5.2±0.5 cm a–1) illustrate the mostly linear trends of increasing elevation. However, the region near the summit (NS: 3.0±0.8cma–1), which had an accumulation low around 1994/95 (Reference McConnellMcConnell and others, 2001), had a decreasing dH/dt for the first 3 years followed by an increase.
At elevations above 2000 m, our dH/dt appear very similar in some regions to those from ATM surveys made between 1993 and 1998 in the south and 1994 and 1999 in the north (Reference KrabillKrabill and others, 2000), but are more uniformly positive over the ice sheet (Fig. 5). The principal region of elevation decreases above 2000 m in both datasets is in the southeast (DS4.1 and 4.2) where, for example, dH/dt = –12.7 ± 1.7 cm a–1 at point SE at 2173 m (Fig. 3a). Our dH/dt results are compared with our calculation of the ATM data by elevation intervals in Table 3. Above 2000 m our average dH/dt of +4.77 cm a–1 is larger than the +0.5 ± 0.5 cm a–1 for the ATM data (Reference KrabillKrabill and others, 2000; Table 3), or the +1.0 ± 0.5 cm a–1 as given by Reference ThomasThomas and others (2001) and revised to +1.4 ± 0.5 cm a–1 (personal communication from R. Thomas, 2005). These differences may be due to the limited spatial and temporal sampling of the ATM data and to sensitivity to seasonal changes in elevation, because the ATM flights made around May and June occur at the time of maximum change in the rate of firn compaction (Reference Zwally and LiZwally and Li, 2002).

Fig. 5. Comparison of dH/dt distribution for Greenland: (a) ERS only; (b) same as in Figure 1b; and (c) produced by interpolation and extrapolation of airborne laser altimeter and ATM surveys data collected in 1993–99 (Reference KrabillKrabill and others, 2000).
Table 3. Comparison of dH/dt for Greenland from this study with ATM results of Reference KrabillKrabill and others (2000). Values listed as computed (some second decimals are not significant)

At Greenland elevations below 2000 m, the pattern of decreases in most areas is in good agreement with the ATM- based values (Fig. 5). Some of the differences near the margins are probably due to the extrapolation/interpolation of ATM values to the ice margins using temperatures at coastal weather stations (Reference KrabillKrabill and others, 2000), compared to our direct extrapolation/interpolation of ERS and ATM data. Our average dH/dt below 2000 m is –8.95 ± 0. 85 cm a–1, which indicates more thinning than our calculation of dH/dt = –6.5 cm a–1 for the ATM data (Table 3). Below 1200 m, which is the approximate equilibrium-line altitude (ELA), the respective dH/dt are –23.88 ± 1.82 cm a–1 for our results and –12.2 cm a–1 for the ATM.
In general, our dH/dt show more thickening at higher elevations and more thinning at lower elevations than the ATM data. Reference KrabillKrabill and others (2000) reported a net ice loss of 51 km3 a–1 (or 45.9Gta–1 using p = 0.9), but were ‘unable to assign errors’ to their estimate. They used a value of dB/dt = 0.5 cm a–1 in the north and 0.4 cm a–1 in the south compared to our overall average of 0.06 cm a–1, which would reduce their mass loss by 6.2 Gta–1. Applying our firn compaction correction reduces their loss by another 23.4 Gt a–1, and applying their revised dH/dt of +1.4 ± 0.5 cm a–1 (from +0.5 ± 0.5 cm a–1) above 2000 m reduces it by another 8.4 Gt a–1 to a net mass loss of only 8 Gt a–1, which is very close to balance.
In contrast, our dH/dt agree within ±1 cma–1 with those reported by Reference Johannessen, Khvorostovsky, Miles and BobylevJohannessen and others (2005) for elevations above 2500 m (Table 4). At lower elevations, their dH/dt are increasingly more positive than both our ERS-only results and our ERS + ATM + optimal interpolation results. Residual differences at the higher elevations may be due to their not applying a backscatter correction that they estimate to be approximately –0.8 cm a–1. However, our less positive dH/dt between 1500 and 2500 m and our more negative dH/dt below 1500m are probably due to the greater coverage of our values derived from ERS only (e.g. 92% vs 71% between 1500 and 2000 m) and our inclusion of values from ATM and optimal interpolation.
Table 4. Comparison of dH/dt for Greenland from this study for all data and for ERS data only with the ERS results of Reference Johannessen, Khvorostovsky, Miles and BobylevJohannessen and others (2005). Values listed as computed (some second decimals are not significant)

Our dH/dt at four sample locations (JI, HG, NM and NI) with elevations of 472–1365 m have elevation decreases of 7.4–42.2 cm a–1. The H(t) for the two locations below the ELA, Humboldt Glacier (HG) and ‘Northeast Greenland Ice Stream’ (NI), show clear seasonal cycles of several meters amplitude, with minima on 24 and 6 August near the end of the summer ablation season. These H(t) clearly illustrate the capability of our analysis techniques to derive realistic H(t) in some of the low-elevation margins of the ice sheets. The two locations just above the ELA, North Margin (NM) and Jakobshavn Isbræ (JI), also have seasonal cycle minima (on 16 September and 15 August) due to the summer melting and firn compaction. The distributions of dI/dt values above and below the ELA and above and below 2000m effectively show increases in the higher elevations and decreases in the lower elevations, with average values shown in Figure 6.

Fig. 6. Histograms of dI/dt for Greenland: (a) above and below the ELA; and (b) above and below the 2000m surface elevation contour.
Nine drainage systems distributed over the NW and NE (DS1.1, 2.1, 2.2), CE (DS3.1), SE (DS4.1), and the SW and CW (DS5.2–5.4, 6.0), covering 74% of the area of the ice sheet, have dM/dt increases that range between +2.6± 0.2 and +10.5 ± 0.5 Gt a–1. Five systems distributed over the NW (DS1.2), NE (DS2.3), CE (DS3.2) and SE (DS4.2, 4.3), covering 22% of the ice sheet, show dM/dt decreases between 0.19±0.04 and 14.9±0.9Gta–1. The estimated change in the remaining system (DS5.1) is essentially zero. The largest mass losses are from three systems in the SE (DS3.2, 4.2 and 4.3), which have a total loss of –34.5 ± 1.5Gta–1. System 5.3, which consists mainly of the Jakobshavn Isbræ drainage basin, shows a net mass gain due to growth in the interior that dominates the thinning near the mouth (Figs 1c and 5a and b), where there is ample evidence of recent rapid thinning (Reference AbdalatiAbdalati and others, 2001) and reports of accelerated thinning particularly in the floating section (Reference ThomasThomas and others, 2003; Reference Joughin, Rignot, Rosanova, Lucchitta and BohlanderJoughin and others, 2003).
The average dH/dt over Greenland is –0.75 ± 0.35 cm a–1. After correction for surface lowering due to firn compaction (dB/dt = –1.50± 0.02 cm a–1) and isostatic uplift (dB/dt = 0. 06± 0.04cm a–1), the average increase in ice thickness is 0. 69 ±0.16 cm a–1 and the estimated dM/dt is slightly positive (+10.8 ± 2.5 Gta–1).
In WA, most of the eastern Ross Ice Shelf drainage system (DS19) extending from the ice divide north of Byrd Station into the ice shelf, is thinning (average dI/dt = –0.7 ± 0.1 cma–1). For example, dH/dt is –7.2 ± 1.1 cma–1 at MI at 682 m just inland of MacAyeal Ice Stream. In the coastal zone from 45° W to 90° W, the dH/dt values are mostly positive on western Palmer Land (DS24) (e.g. +35.7±3.9cma–1 at AP) and south of the Antarctic Peninsula in the western Filchner–Ronne Ice Shelf (DS1) in the range 5–30 cm a–1 (e.g. +23.0 ± 2.5 cm a–1 at CI).
In the Pine Island (DS22) and Smith/Thwaites (DS21) systems, significant thinning is observed as previously reported (Reference Wingham, Ridout, Scharroo, Arthern and ShumWingham and others, 1998; Reference Shepherd, Wingham and MansleyShepherd and others, 2002; Reference ZwallyZwally and others, 2002a) with respective mass losses of 17.2 ± 1.4 and 45.6 ± 1.4Gt a–1, but not as large as the 84± 15Gt a–1 negative mass-flux estimate by Reference ThomasThomas and others (2004). At one location (PG2) at 627 m elevation on Pine Island Glacier where the average dH/dt over the 9 years is –68.9 ± 3.4 cm a–1, the H(t) shows a tripling of thinning rate from 27 cm a–1 for 1992 to March 1995 to 79 cm a–1 for March 1995 to 2001 (Fig. 3b). This increase in thinning rate could be consistent with the observed increase in the velocity of Pine Island Glacier (Reference Joughin, Rignot, Rosanova, Lucchitta and BohlanderJoughin and others, 2003; Reference Rignot, Casassa, Gogineni, Krabill, Rivera and ThomasRignot and others, 2004). However, other H(t) in that region (e.g. PG at 323 m, TG at 774 m and SG at 407 m in Fig. 3b) do not show changes in thinning rates during this period that might provide evidence of acceleration in discharge rates as implied by Reference ThomasThomas and others (2004).
The floating ice in WA is thinning significantly, with average dI/dt ranging from –8.8±5.0cma–1 on northern Ellsworth Land (DS23) and –10.8 ± 1.8 cm a–1 on the eastern Ross Ice Shelf (DS19) to –216± 193cma–1 on the Pine Island system (DS22) and –204± 57cma–1 on the Smith/Thwaites system (DS21). Some thinning is observed on the southern part of the Filchner–Ronne Ice Shelf, but thickness increases in the 5–60 cm a–1 range are dominant for the central and northern parts of the western lobe of this ice shelf. However, although dH/dt for the point near the Ronne Ice Shelf front is positive (RI: +5.3 ± 2.7cma–1), the first 5.5 years show a decreasing elevation followed by a sudden increase of nearly 1 m, after the summer of 1998 when a very large open-water anomaly formed in the sea ice in front of the shelf. The open water is a likely source for a regional accumulation increase and a short-term thickening of the shelf. This large interannual variability is reflected in the relatively large σs of ±50% for this location.
The dH/dt value of –20.4 ± 2.0 cm a–1 on the Larsen B ice shelf (LB) indicates a thinning of about 135 cma–1 prior to break-up. The dH/dt = –17.9 ± 1.8 cm a–1 on the remaining Larsen C ice shelf (LC) indicates a somewhat smaller thinning of about 118 cma–1, within the range of previous analysis (Reference Shepherd, Wingham, Payne and SkvarcaShepherd and others, 2003). The ice shelves on the western side of the Peninsula are also thinning, with dI/dt = –162 cm a–1 on the Wilkins Ice Shelf (WI) and –139 cm a–1 on the George VI Ice Shelf (GI). The shelves along the coast of WA from 110° W to 135° W are also thinning, with dI/dt = –183 cm a–1 on the west Getz Ice Shelf (WG) and –281 cm a–1 on the east Getz Ice Shelf (EG).
In EA, dH/dt are mostly in the range ±5cm a–1 over the interior, with some larger values within a few hundred kilometers of the coast. The patterns of thickening or thinning tend to be spatially coherent over distances on the order of 500 km, with a mixture of areas of thickening and thinning in contrast to the more uniform pattern of thickening recently reported (Reference Davis, Li, McConnell, Frey and HannaDavis and others, 2005). For example, our H(t) at the upper Lambert Glacier (UL) has a uniform linear decrease (–11.4± 1.3cma–1) and many of the dH/dt over the adjacent DS11g and 12g are slightly negative (Fig. 2) compared to the significant dH/dt increases in figure 2 of Reference Davis, Li, McConnell, Frey and HannaDavis and others (2005). Other sample dH/dt at interior points are –4.1 ± 0.7 cm a–1 over the Gamburtsev Subglacial Mountains (GM) and +3.9 ± 0.7cma–1 in Dronning Maud Land (DM). In the coastal zone from 45° W to 180° E, the surface elevations are mostly increasing in the range 5–20cma–1, with exceptions including the –11.6 ±3.8cma–1 on Shirase Glacier (SH), –20.6 ± 5.0cma–1 on Denman Glacier (DG) and –44.8±4.8cma–1 on Totten Glacier (TG). Most of the floating-ice areas of EA show increases in elevation, including +15.0± 1.7cma–1 on the Amery Ice Shelf (AI) and +8.6 ± 0.6 cm a–1 on the western Ross Ice Shelf (WR). The pattern of changes on the Ross Ice Shelf is clearly delineated by the drainage systems, with marked thickening of the ice flowing from EA and thinning of the ice from WA.
Our average thickening for EA (dI/dt = +0.2 ± 0.1 cm a–1) is smaller than the 1.8 ± 0.3 cm a–1 rate reported in Reference Davis, Li, McConnell, Frey and HannaDavis and others (2005), which would be 1.6 cm a–1 if adjusted for our calculated slowing of firn compaction (dC/dt = 0.21 cma–1). Although their dI/dt is eight times as large, their dM/dt increase is only three times as large due to their low estimated density for the added mass as discussed above. While some of the difference may be due to respective methods of constructing the H(t) time series or our interpolated gridpoints, a more likely cause is difference in the methods of time-series analysis to derive dH/dt. We believe our calculated dH/dt more accurately represent the changes in elevation during the measurement period than the results of the autoregression method (Reference Ferguson, Davis and CavanaughFerguson and others, 2004), which may remove interannual variability and misrepresent the actual change during the measurement period. In this regard, we note that the long-term change in figure 1 of Reference Davis, Li, McConnell, Frey and HannaDavis and others (2005) over the measurement period appears smaller than their derived linear trend.
The average dH/dt increase over the total Antarctic grounded ice is only +0.18 ± 0.11 cma–1. After correction for the small surface lowering due to firn compaction (dC/dt = –0.08 ± 0.006cma–1) and isostatic uplift (dB/dt = 0.54± 0.007cm a–1), the average decrease in ice thickness is 0.28 ± 0.11 cm a–1. The changes in WA grounded ice are significantly larger (dI/dt = –2.6± 0. 3 cm a–1 and dM/dt = –46.6±4.4Gta–1) than those in EA (dI/dt = +0.2 ±0.1cma–1 and dM/dt = +16.3 ± 10.7Gta–1), and the overall balance of grounded ice is negative (dM/dt = –30.3 ± 12.1 Gta–1). The changes in floating ice are large in both WA (dI/dt = –13.9± 1.7 cm a–1 and dM/dt = –94.5 ± 11.4 Gta–1) and EA (dI/dt = +22.6 ± 1.5 cm a–1 and +142 ± 10 Gt a–1), with signs corresponding to the respective loss and gain of grounded ice.
Although the overall average ice-thickness changes are small, average dI/dt in particular DS are large (Fig. 4a; Table 2). In Greenland, average dI/dt range from +7.6 ± 0.6 cm a–1 in DS4.1 in the southeast and +7.1 ± 0.2 cm a–1 in Jakobshavn DS5.3 in the southwest to –14.6 ± 1.5 cm a–1 in DS4.2 and –27.3 ± 0.7cm a–1 in DS4.3 in the southeast. In WA, average dI/dt on grounded ice range from +4.0±0.2 cma–1 in the central Ross Ice Shelf DS18 to –22.9± 0.7cma–1 in the Smith and Thwaites DS21. In EA, average dI/dt on grounded ice range from +7.4 ± 1.0 cm a–1 in west Dronning Maud Land DS5 to–14.5 ± 2.7cma–1 in Kemp Land DS8. In WA, average dI/dt on floating ice range from +21.8 ± 1.2 cm a–1 on the Filchner–Ronne Ice Shelf DS1 to –204 ± 57cma–1 in the Smith and Thwaites DS21 and –216 ± 193 cm a–1 in the Pine Island DS22. In EA, average dI/dt on floating ice range from +91.5 ± 10.7 cm a–1 in the Davis Sea DS12, +59.2 ± 8.3 cm a–1 on the west Dronning Maud Land DS5, and +55.1 ± 5.4cma–1 on the central Amery Ice Shelf DS10 to –90.3 ± 20.5 cm a–1 in Terre Adelie DS14. The dominance of negative balances on both floating and grounded ice in WA, and the dominance of positive balances on both floating and grounded ice in EA are illustrated in Figure 4.
Discussion of Overall Mass Changes and Effect on Sea Level
Of the three ice sheets, WA shows the largest imbalance (dM/dt = –47±4Gta–1), which is partially offset by a positive balance in EA (+16± 11 Gta–1), for a net loss of grounded ice from Antarctica (–31 ± 12Gta–1) contributing +0.08 ± 0.03 mm a–1 to sea-level change. The loss from Antarctica is partially compensated by a small gain in Greenland(+11 ±3Gta–1)contributing –0.03 ±0.01 mma–1 to sea-level change, for net mass loss of 20 ± 12 Gt a–1 and a combined sea-level contribution from the three ice sheets of +0.05 ± 0.03 mm a–1. The small mass gain in Greenland is contrary to the widely held view that Greenland is losing significant mass during approximately the same period, but is consistent (within the range of errors) with our reinterpretation of the ATM-based results that indicate the ice sheet was close to balance (–8 Gt a–1). The loss from WA and the gain in EA are remarkably consistent with the respective values of –48 ± 14 and +22 ± 23 Gt a–1 from mass-flux analysis of only about 50% of the Antarctic outlet glaciers under the assumption of only a 5% uncertainty in accumulation rates (Reference Rignot and ThomasRignot and Thomas, 2002).
The contribution to sea-level change is small relative to the potential contribution from ice sheets, not only in relation to the bulk of grounded ice that lies above sea level, but also in relation to the mass flux across the ice–air interface. The loss in Antarctica and the gain in Greenland are each less than about 3% of the respective surface balance estimates, or together less than 1% of the total mass input. The uncertainties are also significantly less than those noted in Reference Huybrechts, Kuhn, Lambeck, Nhuan, Qin, Woodworth and HoughtonHuybrechts and others (2001). The contribution of the ice sheets is also small compared to the most recent estimate of current sea-level rise of 2.8 ± 0.4mma–1 from satellite altimetry (Reference Leuliette, Nerem and MitchumLeuliette and others, 2004), which further confounds possible explanations of the causes of contemporary sea-level rise.
We include estimates of dF/dt (Table 1) for the end-point assumption that the observed dI/dt are occurring only in the firn due to short-term changes in precipitation and that the dynamic balance terms are zero, except in the ablation zone of Greenland where firn compaction is neglected. While there is evidence for decadal changes in precipitation such as the 4% per decade increase in Greenland shown by Reference BoxBox and others (in press) and the long-term trends in Antarctic accumulation mentioned below, we believe evidence of short-term changes over the ice sheets to support this assumption is lacking. Nevertheless, under this assumption, the small mass gain of 11 ±3 Gta–1 in Greenland would be changed to a small mass loss of 18±2Gta–1, because the assumption reduces the estimated gain above the ELA but does not change the loss below the ELA. In Antarctica, the assumption would reduce the mass loss from 31 ± 12 Gta–1 to 14±5Gta–1. The resulting net loss from the three ice sheets would be increased from 20± 12Gta–1 to 32 ± 6Gta–1, giving a slightly larger combined sea-level contribution of +0.09 ± 0.02 mm a–1.
The small positive dI/dt averaged over EA is consistent with evidence of multi-decadal increasing trends in accumulation from ice cores (Reference Mosley-Thompson, Paskievitch, Gow and ThompsonMosley-Thompson and others, 1999; Reference WenWen and others, 2001; Reference Goodwin, De Angelis, Pook and YoungGoodwin and others, 2003) and modeling estimates of long-term trends in Antarctic precipitation (Reference Smith, Budd and ReidSmith and others, 1998). In particular, ice growth in the region of the Antarctic Peninsula may also be due to increasing precipitation during the last century (Reference Smith, Budd and ReidSmith and others, 1998). The marked thinnings in the Pine Island and Thwaites Glacier basins of WA and the Totten Glacier basin in EA are probably ice-dynamic responses to long-term climate change and perhaps past removal of adjacent ice shelves. The correlation between the mass changes of grounded and floating ice in EA and WA may suggest a coherent response of grounded and floating ice to atmospheric and oceanic forcings. The thinning of ice shelves in WA may be fostering increased outflow, and the thickening of ice shelves in EA may be contributing to reduced outflow.
In Greenland, most drainage systems have small mass gains or losses, with the largest mass losses from three systems in the southeast. The most significant division in dM/dt values is between the accumulation zone with a gain of 52.6 ± 1.8Gta–1 above the ELA and the ablation zone with a loss of 41.8 ± 1.8Gta–1 below the ELA (Fig. 5). The gain above 2000 m elevation is 61.2 ± 0.6 Gta–1 and the loss below 2000 m is 50.4 ± 2.5 Gt a–1. These changes indicate a gradual steepening of the ice sheet as expected with climate warming, at a greater rate than previously indicated by the ATM results.
Although the finding of near balance in Greenland might be interpreted to mitigate concern about the future contributions of the ice sheets to sea-level rise, the findings indicate that significant climate-induced changes are taking place. Furthermore, recent ATM surveys indicate a recent increase in coastal thinning (Reference KrabillKrabill and others, 2004), but additional attention needs to be given to effects of increasing precipitation both inland and in coastal regions (Reference Bromwich, Chen, Bai, Cassano and LiBromwich and others, 2001; Reference Hanna, Valdes and McConnellHanna and others, 2001; Reference BoxBox and others, in press). The extent to which the competing processes of inland growth will continue to balance coastal shrinkage, until shrinkage under the predicted climate warming becomes dominant (Reference Huybrechts, Gregory, Janssens and WildHuybrechts and others, 2004), will be seen as observations continue and model predictions are validated or improved.
While the overall net mass changes are small, the changes are generally much larger in particular drainage systems (Table 2; Fig. 4b). Moreover, the ratio of net mass changes to surface balance estimates in many drainage systems (Figs 10 and 12 in Appendix) are up to three orders of magnitude larger than the overall ice-sheet ratios of mass change to mass input (Table 2: (dM/dt)/A jj; Fig. 12). For example, DS5 in west Dronning Maud Land and DS9 to the west of the Amery Ice Shelf in EA have positive mass balances of 49% and 43% respectively over their mass inputs. In contrast, DS21 (Smith and Thwaites Glaciers) and DS22 (Pine Island Glacier) in WA have negative mass balances of 66% and 21% respectively over their mass inputs. In Greenland, DS4.1 in the southeast has a positive balance of 690%, suggesting a large underestimate of the accumulation rate in that system, whereas the adjacent DS3.2 to the north has a negative balance of 110%, and the adjacent DS4.2 to the south has a negative balance of over 1000%. This wide disparity in regional mass balances clearly illustrates the risks of sampling strategies based on studying only the places where the largest changes are taking place.
Overall, our results describe the ice-sheet mass balance during essentially the last decade of the 20th century, and thus provide a baseline for evaluating future changes. Although non-linear variations in H(t) for periods of 3–5 years are evident in some regions, we believe the linear character of most of the dH/dt trends suggests a dominance of multi-decadal mass-balance processes during this period. Clearly, these factors are expected to change (Reference Huybrechts, Gregory, Janssens and WildHuybrechts and others, 2004), perhaps at a greater rate than has been predicted, as recent measurements of increased outflow and increasing precipitation in Greenland may be indicating (Reference AlleyAlley and others, 2003). Therefore, continued comprehensive monitoring of ice elevations is essential to determine, in particular, the relative importance of increasing summer temperatures on both ice melting and dynamic thinning compared to the effect of increasing precipitation on both inland growth and reduction of ablation at lower elevations.
Acknowledgements
We thank the European Space Agency for our selection as ERS investigators and for providing the radar altimeter data and technical information. Data processing and analysis was supported by NASA’s Cryospheric Sciences Program and by ICESat Project Science. We appreciate comments and suggestions from reviewer R.B. Alley and from R.J. Braithwaite. We thank P. Huybrechts, E. Ivins and R. Peltier for digital copies of their bedrock motion data, W. Krabill for a digital copy of the ATM-based dH/dt map, J. Comiso for the digital temperature data, D. Vaughan for digital surface balance data for the Larsen Ice Shelf and I. Allison for his suggestion to account for sea-level rise in calculation of ice- shelf thickness changes.
Appendix

Fig. 7. Distribution of σ s of the derived dH/dt from ERS data for Greenland (a) and Antarctica (b) as described in the text.

Fig. 8. Distribution of dB/dt for Greenland (a) and Antarctica (b) as described in the text.

Fig. 9. Distribution of dC/dt in Greenland (a) and Antarctica (b) calculated with a temperature-driven firn compaction model as described in the text. The firn compaction reduces the surface elevation over the Greenland accumulation zone by 1.71 cm a–1 as the result of climate warming during the measurement period. In WA, the lowering on grounded ice is 1.58 cm a–1 and the lowering on floating ice is 2.79 cm a–1, also due to regional warming, as is the 1.70 cm a–1 lowering on EA floating ice. In EA grounded ice, a small 0.21 cm a–1 surface rise is caused by a small cooling over the inland ice. The dC/dt are computed for all points where A is >25 kgm–2a–1, which in Greenland excluded 121 gridpoints mostly located in the ablation zone, and in Antarctica excluded 92 gridpoints mostly located in the interior of EA where accumulation is small.

Fig. 10. Distribution of net accumulation at the surface based on compiled data. (a) Surface balance rate on Greenland determined for gridpoints (i) by analysis of firn emissivity in the area above the intra-percolation line compared with pit and core data at stations and along traverse routes, bulk corresponding to strata accumulated ~1950–80, and (ii) by accumulation/ablation models output below the intrapercolation line (Reference Zwally and GiovinettoZwally and Giovinetto, 2000, Reference Zwally and Giovinetto2001). (b) Isopleths map of surface balance for Antarctica (in ×100 kgm–2 a–1) drawn on the basis of field data from pits, cores and stake networks at stations and along traverse routes, bulk corresponding to strata accumulated ~1950–2000 (Reference Giovinetto and ZwallyGiovinetto and Zwally, 2000, updated).

Fig. 11. Distribution of net accumulation at the surface interpolated from compilations of field data and models output. (a) Isopleths map of surface balance on Greenland (in ×100 kgm–2 a–1) drawn on the basis of the grid values shown in Figure 10a (Reference Zwally and GiovinettoZwally and Giovinetto, 2001, modified). (b) Surface balance rate on Antarctica determined for gridpoints by interpolation from the isopleths pattern shown in Figure 10b (Reference Giovinetto and ZwallyGiovinetto and Zwally, 2000, updated).

Fig. 12. Distribution of the ratio between net mass budget and net surface accumulation in the grounded-ice and floating-ice areas of each drainage system of Antarctica and Greenland, as listed in Table 2 (column (dM/dt)/A jj ). In Antarctica the estimated gains and losses are smaller than ±50% of the accumulation in 22 of the grounded-ice entities of the 24 systems included in the study, or 97% of their total area, and smaller than ±100% in 13 of the floating-ice entities of the 25 systems included in the study, or 58% of their total area. In Greenland the gains and losses are smaller than ±50% of the accumulation in 11 of the 15 systems included in the study, or 83% of their total area.




















