Coherence maps

An image of the magnitude of the spatially averaged cross-correlation function used to generate the interferograms indicates the level of phase coherence throughout the scenes and is referred to as a coherence map (Reference Zebker and Villasenor.Zebker and Villasenor, 1992). These maps provide a spatial indication of the quality of the interferometric data, with areas of high phase coherence corresponding to bright areas, while areas of low coherence are imaged as dark areas (Fig. 3a and b). The phase-coherence maps of both the 1 and 2 day interferograms indicate there are significant spatial variations in the near-surface properties of the icefield. Differences between the two maps are a result of changes in these properties during the 4 days that span the acquisition period and are also due to the difference in the amount of ice motion observed by the 1 and 2 day interferograms.

Fig. 3. Phase coherence map of (a) the 2 day interferogram and (b) the 1 day interferogram.

The coherence of the icefield from the 2 day interferogram (Fig. 3a) is generally high (>0.7), while the nunataks and rock surfaces at the margin are low (<0.3). The coherence is very low (<0.1) at the termini of all three outlet glaciers, and this low-coherence area extends significant distances up-glacier (HPS-19; 10 km; Glaciar Penguin: 12 km; Glaciar Europa: 3.5 km). The complete loss of coherence in these areas probably results from the large displacements and the rotation of the individual seracs forming the fractured surface (Reference Rignot., Forster. and Isacks.Rignot and others, 1996a). The abrupt loss of coherence at the margins of the two upper tributaries of Glaciar Europa can be explained by a combination of the rotation of the ice within the shear margins and large velocity gradients. This effect is seen to a lesser degree within the right shear margin of Glaciar Penguin.

The loss of L-band phase coherence has been observed approaching the termini of all Patagonian glaciers imaged during the SIR-C mission (Glaciar Moreno (Reference Rott, Stuefer., Siegel., Skvarca. and Eckstaller.Rott and others, 1998; Reference Michel and Rignot.Michel and Rignot, 1999) and four HPN glaciers (Reference Rignot, Forster. and Isacks.Rignot and others, 1996b)). The intense deformation and potential for melting typical of the lower parts of Patagonian glaciers makes classical InSAR phase measurements ineffective near the terminus. However, alternative approaches that use only the two-dimensional cross-correlation of the amplitude images can extend the displacement measurements to the terminus (Reference Rignot., Forster. and Isacks.Rignot and others, 1996a; Reference Rott, Stuefer., Siegel., Skvarca. and Eckstaller.Rott and others, 1998; Reference Michel and Rignot.Michel and Rignot, 1999). While these methods are less sensitive to temporal decorrelation and provide a two-dimensional velocity vector, their accuracy is degraded by more than an order of magnitude (Reference Rott, Stuefer., Siegel., Skvarca. and Eckstaller.Rott and others, 1998). Since this work focuses on areas away from the termini and utilizes the high accuracy required for calculating ice stress and locating flow divides, only the phase InSAR technique is used.

There are substantial differences between the 2 and 1 day coherence maps which, we believe, are related to the difference in time spanned by the interferograms and to the effects of changing surface properties. The shorter time interval of the 1 day interferogram translates into maintaining coherence at faster ice velocities, and a greater tolerance of daily rotation of ice blocks. The net effect of this is to extend the area of high coherence further down the glaciers and to provide higher coherence within the shear margins (Fig. 3b). The large area of low coherence on the lower part of Glaciar Europa cannot be explained by a time-interval change, and the relationship is the opposite of what would be expected for temporal decorrelation, In this area the 2 day coherence is higher than the 1 day coherence. The sequence of amplitude images (not shown) indicates that the radar return in this area is relatively unchanged between the days forming the 2 day interferogram (7 and 9 October) but increases dramatically on the last acquisition (10 October) which is used in the 1 day interferogram.

A large change in the radar return can be caused by a change in the dielectric properties of the glacier, which would alter the phase response and hence cause a low phase coherence. Melting or freezing of a snowpack can cause large changes in radar return (Reference MätzlerMätzler, 1987) and is the suspected cause of the low coherence. Reference Vachon, Geudtner., Mattar., Gray., Brugman. and Cumming.Vachon and others (1996) found very low coherence (<0.2) on all pairs of their ERS tandem dataset of a Canadian temperate glacier when the temperatures were above freezing during the acquisitions. Something similar to the HPS data was observed with an ERS-16 day coherence map having an area of higher coherence than the sequential 3 day coherence map (Reference Zebker, Werner., Rosen. and Hensley.Zebker and others, 1994). From temperature records they concluded the freezing of the soil and vegetation were responsible for the area of low coherence and that freezing or thawing of surfaces, in general, would cause low coherence.

While there are no temperature records or ground observations of Glaciar Europa during this time, an automatic weather station (AWS) was in place on Glaciar Moreno (Fig. 1b) approximately 50 km to the southeast (Reference Takeuchi, Naruse. and Skvarca.Takeuchi and others, 1996). The daily mean temperatures at the Moreno station during the 4 days of the SIR-C acquisitions indicate a warming trend (Table 2). The temperatures are extrapolated to the elevation range of the low-coherence area on Glaciar Europa using a lapse rate determined on Glaciar Moreno (Reference Takeuchi, Naruse. and Skvarca.Takeuchi and others, 1996). There may be errors in values and the timing of the extrapolated temperatures since Glaciar Moreno is on the eastern side of the continental divide. The temperatures suggest that near-freezing conditions may have prevailed between 7 and 9 October, while there could have been more melting on 10 October 1994. Extended melting on the surface of the glacier between the acquisitions of the 1 day coherence map would account for the low-coherence area.

Table 2. Calculated temperatures at 1200 m from AWS data on Glaciar Moreno, Argentina (Reference Takeuchi, Naruse. and Skvarca.Takeuchi and others, 1996)

Icefield surface topography

The DEM generated from the double-difference interferogram is sufficient to remove the topographic phase contribution from the 1 day interferogram in order to construct a velocity map, but, because of its relatively short baseline perpendicular to the radar line of sight (B _n) it cannot be used for detailed topographic analysis (Table 1). The sensitivity of the interferometer to topography is proportional to B _n:

. (2)

where φ _t is the phase contribution due to topography, z is the elevation, θ is the radar incidence angle, k is the wavenumber (2π/wavelength) and R ₀ is the slant-range distance (Reference Joughin, Winebrenner., Fahnestock., Kwok. and Krabill.Joughin and others, 1996b, equation (9)). Each phase cycle (–π to +π) of the double-difference interferogram represents about 370 m of elevation, which translates to about three phase cycles over the approximate elevation range of the icefield in this area (1200 m). In contrast, typical ERS-l interferometers used to generate DEMs (Reference Zebker, Werner., Rosen. and Hensley.Zebker and others, 1994; Reference Joughin, Winebrenner., Fahnestock., Kwok. and Krabill.Joughin and others, 1996b) yield an elevation-to-fringe ratio which is 2–8 times more sensitive to topography. The ratio of Equation (2) can also be used to estimate the error in the interferometric topography (σ _z) introduced by phase noise (σ _φ). Phase noise is calculated from the coherence (γ):

. (3)

where N is the number of looks of the interferogram (N = 0) (Reference Rodriguez and Martin.Rodriguez and Martin, 1992). Phase noise in the double-difference interferogram over the areas of typical coherence (0.6) and areas of low coherence (0.4) yields σ _z of 18 and 36 m, respectively. Errors of this magnitude prevent the DEM from being used for detailed topographic analysis or as a benchmark to estimate future glacier elevation changes. Additional errors from baseline uncertainties, atmospheric delays and receiver clock noise are more difficult to quantify (Reference Rignot., Forster. and Isacks.Rignot and others, 1996a). Local errors may also result from differences in the penetration depth of the L-band signal into the snow/firn and ice, as well as multiple scattering from very rough surfaces such as crevasses, which lengthens the phase path length.

Since there are no topographic maps available for this area, a filtered version (25 pixel median filter) of the DEM is still useful and is shown in Figure 4 draped over an amplitude SAR image. The DEM covers only the icefield and excludes the nunataks and some areas on the ice where coherence values are low or unwrapping errors occurred. The elevations range from 800 m (dark blue), near the area where phase coherence is lost on Glaciar Europa, up to 2200 m (dark red). The approximate locations of the two primary topographic divides on the icefield between Glaciaires Europa and Penguin are indicated as black lines (Fig. 4) and are used in the analysis of the ice divides in the next section.

Fig. 4. A median-filtered DEM of the icefield generated from the double-difference interferogram over an amplitude image. Dark blue is 800 m and dark red is 2200 m. The two black lines on the DEM are the topographic divides between Glaciares Europa and Penguin.

Ice motion

The very short baselines which introduce large errors into the DEM are advantageous for surface displacement measurements. The 28 m perpendicular baseline of the 1 day interferometer (Table 1) yields a sensitivity of 570 m of elevation per phase cycle (Equation (2)) which translates into two cycles of phase for the range of icefield elevations. In contrast, one phase cycle represents 0.12 m of displacement (Equation (1)), implying the 1day interferometer is over 4000 times more sensitive to displacement than to topography. Since the phase of the unwrapped–flattened 1day interferogram is dominated by displacement contributions, only a general DEM is needed to remove the broad-scale topographic phase. The phase-noise-induced errors in the DEM (18–36 m) result in velocity errors of 0.6–1.2 cm d⁻¹ (Reference Joughin, Winebrenner., Fahnestock., Kwok. and Krabill.Joughin and others, 1996b, Equation (15)). The errors of the velocity measurements(σ _ν) due to phase noise (σ _φ) in the 1 day interferogram are related to coherence (Equation (3)):

. (4)

The phase-noise-induced velocity errors (and their corresponding coherences) are 4.6 mm d¹ (0.72) for typical areas of the icefield, 7.3 mm d⁻¹ (0.57) within the shear zones and 14.1 mm d⁻¹ (0.36) at the lower part of Glaciar Europa affected by melting.

The additional errors from baseline uncertainties, atmospheric delays and receiver clock noise also apply to the 1 day interferogram and therefore directly to the velocity measurements. The cumulative effect of these errors is small and can be measured as the velocity of small ice-free regions which are assumed to have zero displacements. Most of the ice-free areas were manually masked because of their very low coherence (<0.2). The rock areas remaining are labeled in Figure 5. The perimeter of all rock areas has apparent velocities of 0 ± 1.0 cm d⁻¹. This velocity range is shown as black in Figure 6. (There are non-rock areas with this velocity range, and their origin is explored in the next section.) The locations of the rock areas span nearly the full extent of range and azimuth, implying any residual tilt in the interferogram from errors in estimating the baseline produces velocity errors less than ±1.0 cm d ^−l. The interior area of a few of the rock outcrops has a measured velocity of –2 cm d⁻¹. This error is greater than the 1.41 cm d⁻¹ phase error calculated for the low-coherence areas, and therefore we can estimate the combined effect of the baseline uncertainties, atmospheric delays and receiver clock noise errors as ≈2 cm d⁻¹. This value serves as an upper bound because it is impossible to determine from the amplitude image if some of the areas labeled bare rock contain the edges of small cirque glaciers with true ice motion.

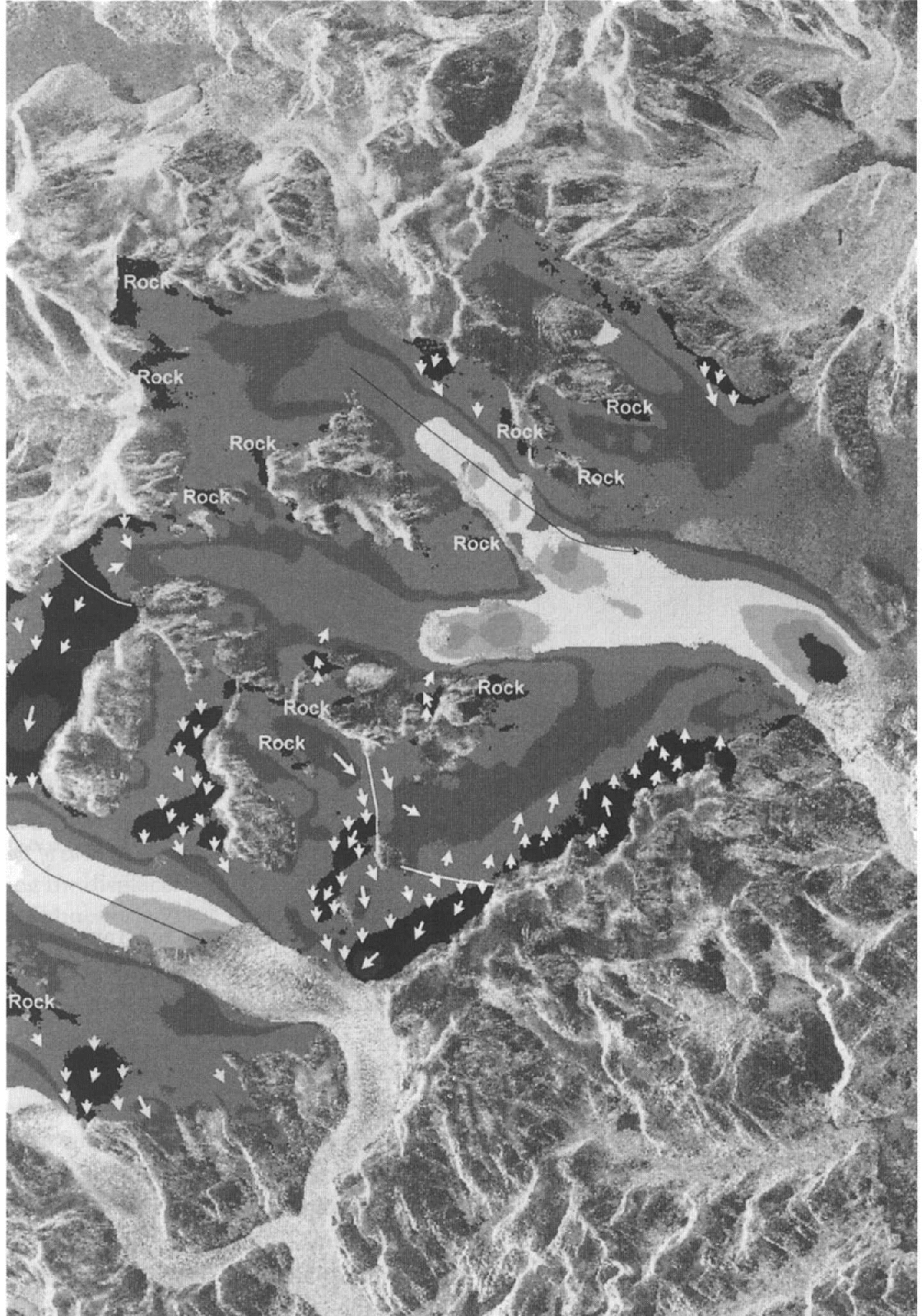
Fig. 5. Model of the flow patterns (white arrows) near the areas of transition from flow toward (dark shades) to flow away from (light shades) the radar illumination direction. The length if the arrows is not proportional to speed. Velocity contours are a gray-scale representation if Figure 6.

Fig. 6. Map of the ice velocity in the radar line if sight (from left). The solid red lines are the topographic divides from the DEM (Fig. 4). The dashed red line is the boundary between the velocity map with topographic phase removed (left) and the velocity map derived directly from the flattened–unwrapped 1 day interferogram (right). The black lines are the locations of the velocity profiles shown in Figures 7–9.

The ice-velocity map (Fig. 6) is spatially limited by the extent of the DEM. The phase of the 1 day interferogram was successfully unwrapped on a larger part of the lower end of Glaciar Europa. In this area the double-difference phase contained many unwrapping errors, and the assumption of steady ice flow over the longer time period is probably not appropriate approaching the terminus. Therefore, no DEM was generated for this area. The 1 day interferogram is dominated by displacement, and the change in elevation across lower Europa is estimated to be <200 m based on control points near the limit of the DEM and the ice front. Therefore, the assumption that the phase is independent of topography results in a relative velocity error of 4.2 cm d⁻¹ (Equations (1) and (2)). This relative velocity field was converted to absolute velocity by adding a phase constant forcing the velocity to be continuous across the boundary (Fig. 6, red dashed line) with the DEM-derived velocity map. Similar extensions could not be added to the Penguin and HPS-19 glaciers because the limits of successful unwrapping for the 1 day and double-difference interferograms coincided.

Radar line-of-sight velocities

The ice-velocity map contains only the component of ice motion in the direction of the radar illumination, but reveals the great spatial variation in velocity within this geometrically complex part of HPS (Fig. 6). The two purple hues represent ice motion toward the radar. The range of colors from blue (low velocity) to red (high velocity) represent motion away from the radar. The narrow range of velocities near zero, which includes the transition from ice motion away from to ice motion toward the radar, is shown in black. While much of the complexity of the map, particularly the change in sign of the velocity, can be attributed to the change in flow direction relative to the radar illumination direction, there are several obvious characteristics of the velocity field worth noting. The velocity patterns of the lower parts of all three glaciers are indicative of a central core of fast-flowing ice bordered by the slower-moving icefield on either side. The same observation was made by SIR-C InSAR for Glaciar San Rafael, Chile (Reference Rignot., Forster. and Isacks.Rignot and others, 1996a), and for Columbia Glacier, Alaska, from photogrammetry techniques (Reference Meier, Rasmussen., Krimmel., Olsen. and Frank.Meier and others, 1985). The ice accelerates toward the glacier termini and reaches a maximum line-of-sight velocity of 0.9, 1.5 and 2.2 m d⁻¹ for the HPS-19, Penguin and Europa glaciers before phase coherence is lost. (These velocities represent the motion in the direction of the radar illumination, from the left of Figure 6 inclined 57° from the horizontal, and therefore underestimate the ice-surface velocity, which is computed along transects in the following subsection.) There are several circular regions of high velocity separated by troughs of slower velocity on the two upper tributaries of Glaciar Europa.

Velocity profiles

In order to construct a complete two-dimensional map of ice velocity, at least one more interferogram with an opposing line of sight is required (Reference Goldstein, Engelhardt., Kamb. and Frolich.Goldstein and others, 1993; Reference Kwok and Fahnestock.Kwok and Fahnestock, 1996). For areas where the flow direction (ζ) and surface slope (ø) is known, the radar line-of-sight velocity (ν _r) can be projected onto the ice surface in the direction of flow yielding an ice-velocity measurement

. (5)

equivalent to measuring the displacement of a feature on the ice surface (Reference Kwok, Joughin. and Jezek.Kwok and Fahnestock, 1996). The assumption of ice motion parallel to the ice surface is valid since the vertical component due to ablation is very small compared with the motion over most of the glacier. The horizontal component of the ice-surface velocity in the flow direction (ν _fl-h) is calculated along the path of three flowlines that are observed on the amplitude image (Fig. 2). The location of the transects is also shown on the ice-velocity map (Fig. 6). The surface slope along the transects is calculated from the median-filtered DEM. The velocity profiles are smoothed using a boxcar-averaging function with a width of 50 pixels (≈750 m). Longitudinal strain rate is computed as Δν _fl-h/ Δd _fl, where d _fl is the distance between velocity measurements along the transect (≈15 m).

Transect A

The ice velocity along the center line of Glaciar Penguin gradually increases from 1.7 to 2.0 m d¹ during the first 3.5 km of the transect before quickly rising to 2.6 m d¹ in the last 1.5 km (Fig. 7a). While the data end approximately 14 km from the terminus, this trend is similar to velocities recorded approaching the termini of other tidewater glaciers (Reference Meier, Rasmussen., Krimmel., Olsen. and Frank.Meier and others, 1985; Reference Naruse, Skvarca., Satow., Takeuchi. and Nishida.Naruse and others, 1995; Reference Rignot., Forster. and Isacks.Rignot and others, 1996a) which can be attributed to a dominance of basal sliding and the diminution of longitudinal back-stress on the terminus (Reference Meier and Post.Meier and Post, 1987). At this distance from the terminus the sharp increase in velocity is more likely the result of an increase in basal sliding, possibly due to an influx of subglacial water from increasing melt at lower elevations along with the availability of crevasse drainage.

Fig. 7. Glaciar Penguin flowline transects of (a) horizontal ice velocity and topography from the median-filtered DEM and (b) longitudinal strain rate: compression (–) and extension (+). The location of the initiation if crevassing as determined from the amplitude image (Fig. 2) is shown in (b). The location if the transect is shown in Figures 5 and 6.

Longitudinal strain rates in the first 3.5 km are slightly higher than the 10⁻² a⁻¹ typical of temperate glaciers (Reference PatersonPaterson, 1994) (Fig. 7b). The small oscillations from compressive to extensional flow may be a reflection of bedrock bumps. The strain rate at the location where crevassing begins along the transect is 0.25 a⁻¹ and indicated by the vertical line in Figure 7b.

The location of crevasse initiation from the amplitude image (Fig. 2) combined with strain rates measured along the center line (Fig. 7b) allow the tensile strength of the ice to be estimated. Reference VaughanVaughan (1993) used published strain-rate measurements from field observations and remote-sensing data of crevassed and uncrevassed locations to estimate temperate- and polar-ice tensile strength. His model assumes crevassing is controlled by the strain rate in the deep ice and hence its constitutive relationship. The firn acts as a thin surface layer contributing little to the strength of the ice mass. The range of tensile strength found from the four temperate glacier studies cited is 90–200 kPa, all values being based on field observations.

The relationship used for converting strain rates to deviatoric stress simplifies to Glen’s flow law of ice under the assumption of only one surface component of strain, as is typically assumed along the center line. The symmetry of the crevasses about the center line (Fig. 2) supports the assumption of minimal lateral strain and therefore the use of the flow law. However, ice fractures in response to the absolute stress and not the deviatoric stress. The relationship between the longitudinal deviatoric stress (σ ^′_L) and the tensile strength of ice (σ _T) is dependent on the failure criteria. Using the maximum octahedral shear-stress (von Mises) criterion (Reference RamsayRamsay, 1967) with the assumption of no lateral strain, we find

. (6)

Applying Griffith’s criterion (Reference Jaeger and Cook.Jaeger and Cook, 1979) predicts

. (7)

The tensile strength of ice can now be estimated from our observations of strain rate by incorporating the flow law with Equations (6) and (7), respectively:

. (8)

. (9)

where

is the InSAR-derived longitudinal strain rate and A is related to the steady-state creep and dependent on temperature, impurities and crystal orientation of the ice.

The observed strain rate at crevasse initiation (0.25 a⁻¹), with A set to Reference PatersonPaterson’s (1994, p.97) recommended value for temperate ice (6.8 × 10⁻¹⁵ s⁻¹ kPa⁻³), implies the tensile strength of the ice is 182 ± 5 and 210 ± 5 kPa from Equations (8) and (9), respectively. (The error estimate is based on the 2 cm d⁻¹ uncertainty in the ice velocity and the effect of the smoothing function on the profiles.) This result, using 15 m pixels to locate the crevassing, is within the range of tensile strengths measured during the field-based studies mentioned above. This also supports Reference VaughanVaughan’s (1993) conclusion that derived tensile strength is not significantly influenced by the resolution of the data.

Transect B

The velocity profile of the south branch of Glaciar Europa follows a flowline that can be traced almost continuously from the amplitude image. Within the first 9 km of the transect the velocities fluctuate dramatically over short distances, reaching a maximum of 2.6 m d⁻¹ near 5 km, then slowing to a near constant speed of 0.4 m d⁻¹ before accelerating to 3.3 m d⁻¹ at the end of the transect (Fig. 8a). The magnitude and fluctuation of these velocities are very similar to those found on Columbia Glacier (Reference Meier, Rasmussen., Krimmel., Olsen. and Frank.Meier and others, 1985, Fig. 13). Beyond 10.5 km, where there is no InSAR DEM because of low coherence in the double-difference interferogram, the surface velocities are derived directly from the flattened unwrapped phase of the 1 day interferogram. The topography in this area is estimated by assuming a constant slope to a control-point elevation near the end of the transect.

Fig. 8. Glaciar Europa south-tributary flowline transects of (a) horizontal ice velocity and topography from the median-filtered DEM and (b) longitudinal strain rate: compression (–) and extension (+). The location of the initiation of crevassing as determined from the amplitude image (Fig. 2) is shown in (b). Velocity and topography to the right of the thick vertical line in (a) are derived from the 1 day interferogram and extrapolated to a control point, respectively. The location of the transect is shown in Figures 5 and 6.

The longitudinal strain rate for this transect can provide insight into the flow dynamics. The peaks at 2.3 and 4.3 km coincide with locations where the valley walls narrow the width of the glacier. This causes transverse compression of the ice, which is compensated by longitudinal extension (Reference PatersonPaterson, 1994). As the valley widens down-glacier, the flow tends to be more compressive. There are two points along the transect where crevassing initiates, with a crevasse-free zone between them (Fig. 8b, vertical lines). At the point near 2 km the strain rate is 0.3 a⁻¹, which translates to a tensile strength of 194 ± 4 and 224 ± 5 kPa from Equations (8) and (9), respectively. This is slightly higher than the tensile strength found on Glaciar Penguin and at the upper end of the range cited above (Reference VaughanVaughan, 1993). Crevassing continues down-glacier until the 2.9 km location where a small compressive region begins and crevasses are no longer detected until the strain rate climbs back to 0.2 a⁻¹ (tensile strength 169 ± 6 and 195 ± 6 kPa from Equations (8) and (9), respectively) at 4.1 km. Below this point it is difficult to detect the presence or absence of crevasses. The reinitiation of the crevassing at a lower strain rate, implying a lower tensile strength, seems reasonable since the ice was previously fractured. The very large compressive strain rate (–1.1 a⁻¹) at 8.3 km is associated with the end of a very steep section (Fig. 8a) corresponding to a bright area in the amplitude image (Fig. 2). This feature is most likely an icefall. The increased noise of the strain rate between 9 and 11 km is a result of low phase coherence in the 1 day interferogram caused by the suspected melting episode discussed above. The strain rate begins to increase at 12 km as the glacier accelerates toward the terminus.

Transect C

The velocity profile of the north branch of Glaciar Europa begins below a gap in the velocity map and DEM which resulted from low coherence (Fig. 9a). This profile is similar to the last 11km of the south-branch velocity profile (Fig. 8a), with local velocity maxima corresponding to steepened topography followed by an acceleration toward the terminus. The flowline from the north tributary ends in the area of maximum velocity, reaching 5.4 m d⁻¹. The longitudinal strain rate (Fig. 9b) is also similar to that of the last 11 km of the south branch (Fig. 8b). Since the transect begins below the initial crevassing location, strain rates from this profile cannot be used to compute tensile strength.

Fig. 9. Glaciar Europa flowline transects of (a) horizontal ice velocity and topography from the median-filtered DEM and (b) longitudinal strain rate: compression (–) and extension (+). Velocity and topography to the right of the thick vertical line in (a) are derived from the 1 day interferogram and extrapolated to a control point, respectively. The location of the transect is shown in Figures 5 and 6.

Flow divides

Since a flow divide is defined as a location where the horizontal component of the ice velocity is zero (Reference PatersonPaterson, 1994), one might expect flow divides tobe identifiable on an InSAR velocity map. Flow divides and their analogous feature on ice caps, flow centers, are found near topographic divides and summits but do not always have coincident locations. A flow divide can be displaced from a topographic divide because of asymmetric bedrock slopes (Reference PatersonPaterson, 1994) or a gradient of net accumulation across the divide (Reference Van der Veen and Whillans.Van der Veen and Whillans, 1992).

Flow divides and flow centers are important glaciological features that are difficult to locate, requiring intensive field measurements. Ice cores for paleoclimatic interpretation are desirable from ice-flow centers where corruption of the time-depth relationship from horizontal motion is minimized (Reference Jaeger and Cook.Van der Veen and Whillans, 1992). In order to measure the total mass balance of a glacier, its surface area must be known. In areas where individual glaciers originate from a common accumulation zone the flow divides must be mapped. The location of flow divides on HPS are additionally significant as they form part of the disrupted boundary between Chile and Argentina.

The numerous large nunataks and the generally ice-free continental divide in the southern part of HPS segregate the outlet glaciers into individual mountain glaciers separated by small flow divides. In this scene there are two segments of the flow divide which cross the icefield, separating ice flowing between Glaciares Europa and Penguin. The topographic divides on the icefield, estimated from the DEM, are shown in Figure 5 as red lines.

There is an area of zero velocity near the upper topographic divide between Glaciares Europa and Penguin which may represent the flow divide. Other zero-velocity bands are the result of ice flow perpendicular to the radar line of sight, but no reasonable model of flow patterns can explain the band of zero velocity near the upper topographic divide (Fig. 6). Therefore, we believe this band of near-zero velocity represents the upper flow divide between Glaciares Europa and Penguin.

There is no similar band of zero velocities near the lower topographic divide between Glaciares Europa and Penguin. The velocity along the topographic divide is at a local minimum and averages about 6 cm d⁻¹. This is outside the expected cumulative error for velocity measurements and must be explained by something other than systematic-errors. The elevation of the two divides may explain the difference. The upper divide is near the highest point on the icefield at 2100 m. The lower divide is separated by a rock outcrop with the lower part straddling a gently sloping plateau at 1400 m. The upper part of the lower divide runs across an ice ridge at 1550 m. At these lower elevations it is conceivable that daily ablation rates approach several cm d⁻¹. This vertical contribution to the radar line-of-sight velocity could be masking the zero horizontal velocity. Another possible explanation for the lack of zero velocities at the lower divide is a non-steady-state condition where one of the glacier’s drainage areas encroaches on the other.

Flow patterns

Thus far two situations have been identified that produce near-zero ice velocity, stationary ice-free areas and ice at a flow divide. The remaining bands of near-zero ice velocity distinguish areas of ice motion toward the radar from areas of ice motion away from the radar. These areas are thought to be locations where the velocity vector is perpendicular to the line of sight and therefore no motion is detected by the interferometer. The location of these low-velocity bands in areas where no flowlines are visible is used to constrain the orientation of the velocity vector in that area. A model of the general ice-surface flow direction is made from the locations of perpendicular flow superimposed on the line-of-sight velocity map (Fig. 6).