Introduction
On the large timescales of ice-sheet flow, the ice is assumed to be incompressible and to obey a non-linearly isotropic viscous constitutive law for the shear response, neglecting the shorter-timescale viscoelastic effects. It has been a common assumption in large-scale ice-sheet modelling that the ice behaves as a simple isotropic viscous incompressible fluid for which, at constant temperature, the deviatoric stress depends only on the strain rate, and the pressure is a workless constraint, not given by any constitutive law, but determined by the momentum balances and boundary conditions. Such a viscous law is necessarily isotropic by material frame indifference, and neglects fabric evolution (induced anisotropy). Flow solutions incorporating fabric evolution have been much more restricted. The present analysis addresses only the flow with the isotropic viscous law which still dominates large-scale modelling.
The isotropic viscous law has a general quadratic representation, with alternative, but equivalent, stress and strain-rate formulations, as discussed by Reference MorlandMorland (1979). However, it is still common practice to ignore the quadratic term and adopt a simple relation proposed by Reference NyeNye (1953), in which the deviatoric stress is coaxial with the strain rate, and which depends on only one of the two deviatoric stress (or strain-rate) invariants. Reference GlenGlen (1958) (acknowledging F. Ursell) presented the quadratic viscous relation for the strain rate, and noted that Reference SteinemannSteinemann’s (1954) combined compression and shear data were inconsistent with the simple form, so that dependence on a second invariant, or the quadratic term, or both, is necessary. Standard single-stress component tests, uniaxial compression or simple shear, are not sufficient to determine the general form, nor can they verify the validity of the simpler coaxial form. The determination of two response functions with two invariant arguments requires biaxial or combined shear and compression tests. While combined compression and shear tests have been conducted (e.g. Reference Li, Jacka and BuddLi and others, 1996; Reference Warner, Jacka and LiWarner and others, 1999), there has been no attempt to correlate data with other than the simple coaxial form. Prompted by the personal communication from W.F. Budd, T.H. Jacka, J. Li and R.C. Warner of their recent unpublished exposition of such tests, Reference MorlandMorland (2007) showed that confined and unconfined compression combined with shear tests can check the consistency of the general quadratic form, independent of the actual response functions, assess the significance of the contribution made by a quadratic term and then determine the two response functions of two invariant arguments.
A general isotropic viscous relation including the quadratic term has yet to be incorporated into the flow equations for an ice sheet, but would certainly yield changes from the simple coaxial form. The commonly adopted reduced model equations are the leading-order balances of an asymptotic expansion in a small parameter arising from a dimensionless viscosity magnitude in the coaxial form, which, in turn, defines the small surface slope magnitude or sheet aspect ratio (shallow-ice approximation). Reference MorlandMorland (2007) showed that with the quadratic relation, the relative magnitudes of the stress components are different to those found using the coaxial form. However, the same leading-order momentum balances, and their explicit depth integrations to yield the same expressions for the pressure and horizontal shear stresses, are obtained, but with different error magnitudes. The resulting expressions for the velocity gradients with depth cannot be explicitly integrated, so no expressions for the velocity fields are available to incorporate into the surface and bed kinematic conditions to obtain a differential equation for the surface profile. It was also noted that the same problem arises with the simple coaxial form if the response function depends on two invariants, which is the minimum generalization implied by Reference SteinemannSteinemann (1954).
The asymptotic analysis of the reduced model for a coaxial isotropic viscous relation with dependence on both second and third principal invariants of deviatoric stress or of strain rate is presented here, on the assumption that the third invariant dependence does not dominate the second invariant dependence. It is found, then, that the leading-order balances do allow explicit depth integrations of the velocity gradients so that surface and bed conditions can be applied to determine a differential equation for the surface profile; the simplification of the reduced model. This does, of course, depend on knowing how the single response function depends on both invariants, which has yet to be determined. However, uniaxial compression data can be weighted between dependence on the second and third invariants, and Reference Smith and MorlandSmith and Morland’s (1981) polynomial correlation of Reference GlenGlen’s (1955) data in terms of the second invariant is here modified to include both dependencies with an arbitrary weighting factor. Steady radially symmetric reduced model flows over a flat bed are determined for different weighting factors to illustrate the possible significance of the third invariant dependence, with a prescribed temperature distribution and an elevation-dependent surface accumulation/ablation, for modest and large basal friction coefficients. It is found that the third invariant dependence does not have a large influence on the ice-sheet profiles, though the influence is greater for the large basal friction, essentially because the non-linear viscous terms are small for the modest shear stresses arising in these examples. This would not follow for larger shear stresses arising near significant bed topography.
The Isotropic Viscous Relation
Let σ denote the Cauchy stress tensor and ![]() the deviatoric stress tensor, then
the deviatoric stress tensor, then
where p is the mean pressure and I is the unit tensor. Let D denote the strain-rate tensor, the symmetric part of the velocity gradient tensor, which has zero trace by incompressibility. The dependence on temperature, T, is assumed to be given by a rate factor, a(T), by replacing D by an effective strain rate, ![]() , defined by
, defined by
where a(T) is an increasing function of T; that is, the actual strain rate at a given stress increases with temperature.
The coaxial frame-indifferent viscous relation (necessarily isotropic) between ![]() and
and ![]() can be expressed in two alternative, but equivalent, forms of the Rivlin–Ericksen representation between tensors with zero trace:
can be expressed in two alternative, but equivalent, forms of the Rivlin–Ericksen representation between tensors with zero trace:
where ![]() are the second and third principal invariants of
are the second and third principal invariants of ![]() /D
0 and J
2, J
3 are those of
/D
0 and J
2, J
3 are those of ![]() /σ
0, defined by (omitting the minus sign in the second invariant for convenience),
/σ
0, defined by (omitting the minus sign in the second invariant for convenience),
The units σ 0 and D 0 are chosen, with unit rate factor, a, at the melting temperature, so that the constitutive functions, and ϕ, are of order unity for deviatoric stresses and strain rates arising in typical ice-sheet flows:
From (3), ϕ and ψ, and their invariants, satisfy the relations
The pressure, p, is a workless constraint not given by a constitutive law, but determined by momentum balance and boundary conditions. While the expansions (3) are equivalent, there is no explicit algebraic inversion. It is the stress formulation (3)1 which is required for substitution in the momentum balances of a general ice-sheet flow.
The pioneering experimental work of Reference GlenGlen (1952, Reference Glen1953, Reference Glen1955, Reference Glen1958) and Reference SteinemannSteinemann (1954) was used to construct power laws for a simplified form of (3) proposed by Reference NyeNye (1953), namely
in which D is coaxial with ![]() , and there is only one response function, ψ, depending on only one invariant, J
2, which is a measure of the shear stress squared. The tests were mainly on polycrystalline ice at constant temperature with randomly oriented crystals, in either unconfined compression or simple shear, so that only one function of one argument could be inferred.
, and there is only one response function, ψ, depending on only one invariant, J
2, which is a measure of the shear stress squared. The tests were mainly on polycrystalline ice at constant temperature with randomly oriented crystals, in either unconfined compression or simple shear, so that only one function of one argument could be inferred.
Comparisons of known datasets at the time were made by Reference Smith and MorlandSmith and Morland (1981), which demonstrated wide differences. The form (8) was constructed from Glen’s (1955) uniaxial compression data at near-melting temperature over a shear stress range 0–5 × 105 N m–2, 0 ≤ J 2 ≤ 25, showing that a three-term fifth-order polynomial representation, with finite viscosity at zero stress, was a much closer correlation than a power law with infinite viscosity at zero stress:
They also derived an accurate representation for a(T) from data presented by Reference Mellor and TestaMellor and Testa (1969) for temperatures between melting and 60 K below melting, and showed a good simplifying approximation over the range of practical significance from melting to 40 K below melting is
where [20 K] is a typical temperature-change magnitude over an ice-sheet depth, and the dimensionless temperature, ![]() is zero at melting, and –2 at 40 K below melting.
is zero at melting, and –2 at 40 K below melting.
While the uniaxial data correlation, (9), assumes dependence on J 2 alone, and cannot distinguish dependence on J 2 and J 3, it can theoretically be separated additively into dependence on both with an arbitrary weighting factor. In terms of uniaxial compressive stress, σ,
Hence the uniaxial data correlation, (9), can be equivalently expressed by the additive decomposition
for arbitrary weighting, α (0 ≤ α ≤ 1), where α = 1 denotes pure J 2 dependence and α = 0 pure J 3 dependence. A multiplicative decomposition has not been considered. The viscous function given by (13) and (14), together with the rate factor (11), will be adopted to determine the influence of J 3 dependence on reduced-model steady radially symmetric ice-sheet flow solutions.
Reduced Model for Ice-sheet Flow
The ice is assumed incompressible with density ρ = 918kgm–3. Now let the rectangular Cartesian spatial coordinates, x, y, z, where the z axis points vertically upwards, and the corresponding velocity components, u, v, w, be dimensionless with units d
0 and q
0, respectively. These are, respectively, an ice-sheet thickness magnitude and a surface accumulation magnitude, so the dimensionless velocity gradient and strain rate, ![]() have units q
0/d
0. Define dimensionless stress,
have units q
0/d
0. Define dimensionless stress, ![]() with units of a typical overburden pressure, ρgd
0, where g is the gravity acceleration, 9.81 m s–2. Then
with units of a typical overburden pressure, ρgd
0, where g is the gravity acceleration, 9.81 m s–2. Then
The isotropic viscous relations (3) are now expressed by

In relation (16), ε 2 defines a very small dimensionless viscosity magnitude, given in (19) and ϑ is an order unity dimensionless parameter. The small parameter, ε, is that introduced by Morland and Johnson (1980) and Reference MorlandMorland (1984) to derive the leading-order balances (reduced model) for ice-sheet flow. To obtain a finite-span ice-sheet profile from the leading-order balances, it is necessary to introduce the coordinate and velocity scalings

where the upper-case variables are order unity, and derivatives with respect to X, Y, Z do not change orders of magnitude from that of the dependent variable. This requires that the bed topography slope does not induce greater X and Y derivative magnitudes. The corresponding asymptotic analysis when bed topography is of small slope, but larger than ε, (i) induces greater local magnitudes (presented by Reference MorlandMorland (2000, Reference Morland2001) for plane flow and Reference Cliffe and MorlandCliffe and Morland, 2002 for radially symmetric flow), (ii) follows for three-dimensional flow and (iii) extends to the isotropic viscous relation (16). Here it is supposed that the bed topography is as smooth as the surface and does not induce greater magnitudes when the reduced model for the simple viscous relation (8) has error O(ε 2). Note that D occurs only through the effective strain rate D defined by (2); that is, divided by a which can become very small in cold upper regions of the sheet, but Reference MorlandMorland (1984) argued that this was compensated by very small strain rates there, so the formal expansion in ε, ignoring the magnitude of a, is valid.
With the scalings (20),

are all order unity, while

are both O(ε –1) with the leading-order expressions shown having relative errors O(ε 2). Then, to leading order with relative errors O(ε 2), using (17),
From (16) and (18), with relative error O(ε 2),
The momentum balances and equilibrium equations due to the very small inertia terms, are
With the above leading-order stress expressions, these become, with error O(ε 2),
To leading order, neglecting terms of order O(ε 2), the traction-free surface, Z = H(X, Y, t), conditions are
where t denotes a dimensionless time with units d 0/q 0, and (34), (32), (33) can be explicitly integrated with respect to Z from the surface to yield the familiar stress expressions

Now (27) and (28) show that J
3 is of order εJ2, so neglecting O(ε) compared to unity ψ(J
2, J
3) is approximated by (J
2, 0), and similarly, by (23) and (24), ![]() is approximated by
is approximated by ![]() consistent with (7). Hence, with relative error of order ε, relation (16)2 gives
consistent with (7). Hence, with relative error of order ε, relation (16)2 gives

where, using (36) and (27),
Thus, provided that ψ(J 2, J 3) is known, so ψ(J 2,0) is known, depending only on J 2, Equations (37) and (38) are the familiar reduced model equations which can be integrated explicitly from bed to surface. Then application of the bed kinematic and sliding conditions yields the usual partial differential equation for H(X, Y, t). However, in the case ψ = ψ(J 3), independent of J 2, (37) with (28) gives velocity derivatives depending on all the deviatoric stress components, not just those in (36) determined by the leading-order momentum balances, and explicit depth integration of (37) is no longer possible. That is, the case α = 0 in (14) with J 3 ≡ 0 does not determine a pure J 3-dependent solution.
The combined J 2 and J 3 dependence will now be illustrated for steady radially symmetric flow, when an ordinary differential equation is obtained and solved for the surface profile, H(R), so the influence of the weighting factor, α, in the viscous function, ψ, defined by (13) and (14) can be demonstrated.
Radially Symmetric Flow
Although axially symmetric flow has dependence on only one horizontal coordinate, it does incorporate lateral spreading, and is thus a more realistic illustration of ice-sheet flow than plane flow. This has already been exploited in many theoretical/numerical illustrations (Reference MorlandMorland, 1997; Reference Cliffe and MorlandCliffe and Morland, 2000, Reference Cliffe and Morland2001, Reference Cliffe and Morland2002, Reference Cliffe and Morland2004; Reference Morland and StaroszczykMorland and Staroszczyk, 2006), where details of the following formulation are presented.
In cylindrical polar coordinates (r, θ, z), the physical components of an axisymmetrical flow are (u, 0, w), and the scalings analogous to (20) for steady flow are
with corresponding scaled non-zero strain-rate components

where the ![]() approximation has a relative error O(ε
2). The dominant scaled deviatoric stress component is then
approximation has a relative error O(ε
2). The dominant scaled deviatoric stress component is then ![]() and the analogues of (32), (33), (34) and (35) are
and the analogues of (32), (33), (34) and (35) are
and (36), (37) and (38) become
With the isotropic viscous relation given by (13), (14), (9) and (10),
which is simply the form (9), (10) used in the previous applications with the coefficients ψ 1 and ψ 2 scaled by α. The limit α = 1 is exactly the pure J 2-dependent form (9), and the limit α = 0 is pure J 3 dependence, equivalent to the linearly viscous case with ψ ≡ ψ 0. Illustrations are presented in the next section for a set of α values between 0 and 1.
Incompressibility, trace(D) = 0, is satisfied identically by
where Ω(R, Z) is the stream function. Integration of (44) and (46) from the bed Z = F(R), where F′(R) = ß is assumed to be order unity (the bed topography slope does not exceed ε in magnitude), gives
where subscript b denotes evaluation on the bed, and

where the superscript ′ on variables denotes evaluation at the dummy integration variable Z′. The vertical velocity, W, is then given by (46)3, and P and ![]() by (43), once H, Γ and Ω are determined.
by (43), once H, Γ and Ω are determined.
The kinematic conditions on the surface and bed are
where subscript s denotes evaluation on the surface, Q(R, H) is the surface accumulation (inward volume flux, negative in ablation zones), depending on R and elevation H in general, and B is the basal melting (outward volume flux, negative if refreezing), in the dimensionless units. Finally, on Z = F(R), the adopted basal sliding law is
where Λ is a non-dimensional order unity or greater friction coefficient (Λ → ∞ is the no-slip limit), Λ(0) ≠ 0 and the proportionality to Pb ensures bounded surface slope at the margin where Pb = 0. Equation (51) gives Ub in terms of Δ and Γ. Differencing relations (49) and (50) and using relations (47) and (51) yields the second-order ordinary differential equation

for H(R) on the unknown span 0 ≤ R ≤ R M, where R M is the unknown margin radius. Asymptotic analysis relates the surface slope at the margin,
to margin values of ß, A and ![]() denoted by the subscript M. The second derivative H″(R) given by differential equation (52) is indeterminate at the margin where Δ → 0, and at the divide where R → 0, but further asymptotic analysis determines the required limits, given, for example, in Reference Cliffe and MorlandCliffe and Morland (2002).
denoted by the subscript M. The second derivative H″(R) given by differential equation (52) is indeterminate at the margin where Δ → 0, and at the divide where R → 0, but further asymptotic analysis determines the required limits, given, for example, in Reference Cliffe and MorlandCliffe and Morland (2002).
The numerical solution is obtained by expressing the second-order equation as four first-order differential equations for H, Γ, RM and H D, where H D is the elevation at the divide R = 0, on a fixed span 0 ≤ t ≤ 1 with the change of variable R = R M t. Then R M and H D are unknown constants, with zero derivative with resepct to t. The four equations are integrated from both ends t = 0 and t = 1 starting with trial R M and H D and iterating until H and Γ match accurately at an interior point.
Illustrations
The simple, physically plausible, surface accumulation/ ablation distribution adopted is an elevation-dependent example with large margin ablation, introduced by Reference MorlandMorland (1997) and used in later papers:
Decay height scale H = 0.25 corresponds to h = 500 m. The equilibrium height (snowline) where Q = 0 is at H = 0.64, corresponding to h = 1280 m. The basal melting, B, is assumed zero, so ![]() is simply Q.
is simply Q.
The temperature distribution adopted was also introduced by Reference MorlandMorland (1997) and used in later papers:x

which depends on surface elevation and depth below the surface. The corresponding thermal boundary conditions are

with the realistic properties that the surface temperature decreases at a rate of 0.8 K per 100 m rise, a uniform heat flux into the base equivalent to a temperature gradient of 0.5 K per 100 m, and that the Laplacian of T, arising in the energy balance, is bounded.
Two constant friction coefficients are considered: a modest Λ ≡ 25 and a larger Λ ≡ 100.
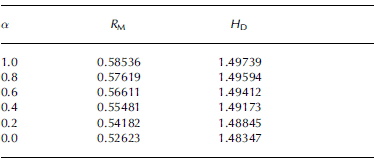
Tables 1 and 2 show the values of R M and H D for different values of the invariant weighting parameter, α, for Λ ≡ 25 and Λ ≡ 100, respectively. The case α = 0 is the linearly viscous limit, and not an actual pure J 3-dependent solution. For the friction coefficient Λ ≡ 25, Table 1 shows that R M decreases by only 3% as α decreases from 1 to 0, and H D increases by only 0.45%. For Λ ≡ 100, Table 2 shows that RM decreases by 10% as α decreases from 1 to 0, and now H D decreases, by 0.9%. While the larger basal friction enhances the differences as J 3 dependence increases, the overall change is still not large. The corresponding surface profiles for the different values of α are similarly close. Essentially, at the shear stress levels near the bed, where they are at their greatest, the magnitude of the invariant J 2 is not sufficiently large for the non-constant terms of the isotropic viscous relation (13) to dominate, so the non-linear dependence on J 2 is not very significant even when there is no J 3 dependence. This will not be the case over significant bed topography where greater shear stresses occur, but where the reduced model is not valid.
Table 1. Margin span, R M, and divide height, H D, for different α with Λ ≡ 25

Table 2. Margin span, R M, and divide height, H D, for different α with Λ ≡ 100
Conclusions
The commonly adopted reduced model (shallow-ice approximation) equations are the leading-order balances of an asymptotic approximation using the small surface slope magnitude or aspect ratio as small parameter. They are valid only when the bed topography also has small slope; the full equations are necessary otherwise. Until now the reduced model has been applied with a coaxial isotropic viscous law dependent only on the second principal invariant of the deviatoric stress. Here, the asymptotic analysis is extended to a coaxial isotropic viscous relation with dependence on both second and third principal invariants. This shows that the leading-order momentum balances are the same, allowing explicit depth integration to yield the same expressions in terms of the surface profile for the pressure and horizontal shear stresses. Further, the third invariant dependence does not explicitly change the velocity gradient relations so that they can also be integrated through the depth as before, leading to the usual reduced model equation for the surface profile. This is explicitly determined for steady axially symmetric flow, yielding the usual second-order differential equation for the surface elevation on an unknown span. An isotropic viscous relation with dependence only on the second invariant, determined by correlation with uniaxial compressive stress data, is here weighted additively between second and third invariant dependence with a variable weighting parameter. A set of steady radial solutions has been constructed with different values of the parameter to explore the influence of third invariant dependence with modest and large basal friction. It is found that the third invariant dependence does not have a large influence on the ice-sheet profiles in these reduced-model examples, essentially because the non-linear terms of the viscous relation are not large, though greater with the larger basal friction. Third invariant dependence would have more influence over significant bed topography where larger shear stresses occur, but where the reduced model is not valid.






