List of Symbols
-
α Iterative parameter in Van der Kamp model
-
A Non-linear parameter reflecting turbulence in borehole
-
b Iterative parameter in Van der Kamp model
-
bSL Thickness of subglacial aquifer (m)
-
D Distance to constant-head boundary in Guyonnet method (m)
-
F Parameter reflecting viscous loss in borehole
-
g Acceleration of gravity (9.81 ms–2)
-
h Displacement of hydraulic head in subglacial aquifer (m)
-
H Displacement of hydraulic head in borehole in low-transmissivity models (m)
-
H0 Initial hydraulic head displacement in low-transmissivity models (m)
-
K Subglacial hydraulic conductivity (ms–1)
-
L e Effective length of borehole water column (m)
-
n Index of iteration in Van der Kamp model
-
rA Radial distance from centre of borehole (m)
-
r BH Borehole radius (m)
-
rF Radius of borehole filter (m)
-
S Subglacial storage coefficient
-
t Elapsed time of slug test (s)
-
tC Time of match in Cooper–Bredehoeft method (s)
-
tD Dimensionless time in Kipp model
-
tdev Time of 1% deviation in Guyonnet method (s)
-
T Subglacial transmissivity (m2 s–1)
-
w Displacement of hydraulic head in borehole in high-transmissivity models (m)
-
w 0 Initial water-level displacement in high-transmissivity models (m)
-
α Dimensionless storage parameter in Cooper–Bredehoeft model
-
α K Dimensionless storage parameter in Kipp model
-
β Dimensionless time parameter in Cooper–Bredehoeft model
-
βK Dimensionless time parameter in Kipp model
-
λ Damping constant in Van der Kamp model (s–1)
-
σ Skin factor in Kipp model
-
ζ Damping factor in Kipp model ω Angular frequency of oscillation in van der Kamp model (Hz)
1. Introduction
Slug testing in glacier boreholes has the potential to yield important information about hydraulic properties of subglacial drainage systems (Reference Stone and ClarkeStone and Clarke, 1993; Reference Iken, Fabri and FunkIken and others, 1996; Reference Stone, Clarke and EllisStone and others, 1997; Reference Kulessa and MurrayKulessa and Murray, 2003). The method is identical to slug tests routinely applied to confined or unconfined groundwater aquifers. It involves artificial displacement of the steady-state borehole water level (WL), typically by insertion (falling-head test (FHT)) or removal (rising-head test (RHT)) of a sealed pipe to displace a volume of water, and monitoring the subsequent WL recovery (e.g. Reference Kruseman and de RidderKruseman and de Ridder, 1994). The characteristics of the recovery signal serve as indicators of subsurface hydraulic conditions, and can be analyzed for hydraulic properties of the borehole–aquifer system. At Haut Glacier d’Arolla, Valais, Switzerland, unconsolidated, water-saturated sediments of varying thickness have temperate ice as an upper boundary and bedrock as a lower boundary (e.g. Reference Hubbard, Sharp, Willis, Nielsen and SmartHubbard and others, 1995; Reference Harbor, Sharp, Copland, Hubbard, Nienow and MairHarbor and others, 1997). This situation compares well with that of a conventional confined aquifer (e.g. Reference FetterFetter, 2001). The underlying assumptions of this analysis are that the borehole is hydraulically well connected to the aquifer, implying that a change in aquifer hydraulic head will instantaneously result in an equivalent change in borehole WL, and that there is negligible lateral or vertical leakage into the aquifer. Such fluctuating boreholes (Reference SmartSmart, 1996) are commonly characterized by a noticeable WL drop when the glacier bed is reached during drilling, as well as by marked daily WL variations. In contrast, unconnected boreholes are typically water-filled and non-fluctuating (Reference SmartSmart, 1996).
Three distinct types of slug-test response may be expected, chiefly depending on borehole water-column length and aquifer transmissivity, which together determine the degree of water-column inertial effects. The latter are negligible in the overdamped case (exponential, nonoscillating decay) and significant in the underdamped case (exponential, oscillating decay), with critical damping representing the transitional response (Reference Bredehoeft, Cooper and PapadopulosBredehoeft and others, 1966). A coupled borehole–aquifer flow system of low transmissivity and small water-column length is likely to produce an overdamped response, while an underdamped response may be expected if transmissivity is high and water-column length is large (Reference Bredehoeft, Cooper and PapadopulosBredehoeft and others, 1966). In the overdamped case, water-flow rates in the borehole–aquifer system are commonly small enough for turbulent effects to be neglected, supporting the use of linear slug-test models. Such models are analytically attractive, involving manual matching of observed responses with type curves in the simplest case, and have been widely used in groundwater studies for several decades (Reference ButlerButler, 1997). In contrast, in the underdamped case, water-flow rates could in some instances be so large that turbulence occurs, requiring the use of non-linear models.
Previously a unified model, allowing for any degree of damping of slug-test responses, was developed specifically for application in glaciology (Reference Stone and ClarkeStone and Clarke, 1993; Reference Stone, Clarke and EllisStone and others, 1997). Application to borehole response tests conducted at Trapridge Glacier, Yukon Territory, Canada, together with extensive sensitivity analyses, revealed that non-linear effects in the entire borehole–subglacial-aquifer flow system were not of concern during slug tests. Motivated by this conclusion, the present study aims to investigate the use of established, linear slug-test models in estimating subglacial hydraulic properties. This would allow rapid interpretation of slug tests using either simple manual analysis or widely available ‘linear’ software packages, increasing the appeal of this technique in hydro-glacial investigations.
We initially ascertain that non-linear effects are not prevalent in our data. The bulk of this study then aims (i) to demonstrate the application of a range of linear slug-test models that have been particularly popular in groundwater studies (Reference Cooper, Bredehoeft and PapadopulosCooper and others, 1967; Reference Van der KampVan der Kamp, 1976; Reference KippKipp, 1985; Reference Guyonnet, Mishra and McCord.Guyonnet and others, 1993) to our data and (ii) to estimate the hydraulic properties of the subglacial sediments at the glacier along a transect traversing a major subglacial channel.
2. Slug-Test Methods
2.1. Borehole–subglacial-aquifer flow system
Many different slug-test models have been developed in groundwater studies, each focusing on a particular physical scenario defined by the properties of the well and the aquifer (e.g. Reference ButlerButler, 1997). Choosing the right model for the particular physical scenario to be investigated is important to obtain reliable estimates of hydraulic properties. The conceptual geometry of the borehole–subglacial flow system considered here is illustrated in Figure 1. A borehole of radius rBH is connected to the subglacial aquifer of thickness bSL via a fully penetrating filter of radius rF. The water level is initially displaced by an amount H0 due to slug insertion, and subsequently gradually returns (H(t)) to the equilibrium WL (solid line in Fig. 1). The filter accounts for subglacial excavations due to sediment flushing and clogging in the vicinity of the borehole base as the hot-water drill reaches the glacier bed (e.g. Reference Stone and ClarkeStone and Clarke, 1993). It therefore represents an annulus of larger hydraulic conductivity than the outlying subglacial aquifer. The term borehole face is used to describe the cylindrical interface between the filter and the aquifer, and ice and bedrock bounding the borehole water column and the aquifer are assumed to be impermeable (Fig. 1). The rate of slug-induced water flow in the subglacial aquifer is strongly dependent on its transmissivity (T given by hydraulic conductivity (K) × aquifer thickness (b SL)), which may therefore be estimated from appropriate analysis of recovery curve characteristics. Particularly suitable and popular linear slug-test models for the present physical scenario are the Cooper–Bredehoeft (Reference Cooper, Bredehoeft and PapadopulosCooper and others, 1967), Reference Van der KampVan der Kamp (1976) and Reference KippKipp (1985) methods (e.g. Reference ButlerButler, 1997), which are adapted here to analyze overdamped, underdamped and critically damped responses, respectively.

Fig. 1. Borehole-subglacial flow system geometry.
As considered in section 1, the models for the analysis of slug-test responses are applicable to either low-transmissivity or high-transmissivity aquifers. Linear models may be used in either case if turbulence in the borehole–aquifer flow system is negligible. If slug-induced turbulence is not negligible, as observed previously in some high-transmissivity aquifers (e.g. Reference ButlerButler, 1997; Reference McElwee and ZennerMcElwee and Zenner, 1998), non-linear models must be used. Since these approaches are well established and covered in the pertinent groundwater literature (e.g. Reference ButlerButler, 1997), we present only a brief summary here, focusing on relevant model characteristics.
2.2. Low-transmissivity aquifers
2.2.1. Cooper–Bredehoeft method
Assuming that transient flow in a low-transmissivity aquifer is confined and cylindrical, occurring radially out of, and back into, the borehole face, the hydraulic head in the aquifer (h) is appropriately described by (Reference Cooper, Bredehoeft, Papadopulos and BennettCooper and others, 1965):
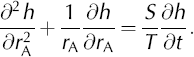
Here, S is the storage coefficient (the pore volume change per unit surface area of the glacier bed per unit head change) and rA is the horizontal distance from the axis of the borehole filter. Equation (1) is based on the conservation of fluid volume, incorporating aquifer and fluid compressibility in the storage term, combined with Darcy’s law, thus neglecting turbulence and assuming a homogeneous aquifer.
The Cooper–Bredehoeft model is a particularly popular method for the analysis of overdamped slug-test responses in low-transmissivity, confined aquifers (e.g. Reference ButlerButler, 1997, p. 57). This method connects transient changes in hydraulic head in the aquifer (h(rA, t)) with those in the borehole (H(t)), induced by slug insertion or withdrawal, considering continuity of water flow at the borehole face (where rF = rA) and neglecting water-column inertia:
The Cooper–Bredehoeft model assumes that well losses are negligible (h(rF,t) = H(t) for t > 0), and that the slug is introduced or withdrawn instantaneously (h(r A,0) = 0 for rF < rA < ∞; H(0) = H0). It is also assumed that there are no flow boundaries within the portion of the aquifer influenced by the slug test (h(∞,t) = 0 for t > 0), and that elastic storage mechanisms, as expressed by S in Equation (1), affect slug-test responses. The Cooper–Bredehoeft model considers that
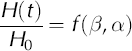
where
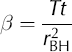
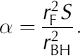
Here, β is the dimensionless time parameter and α is the dimensionless storage parameter. Reference Cooper, Bredehoeft and PapadopulosCooper and others (1967) and Reference Papadopulos, Bredehoeft and CooperPapadopulos and others (1973) plot H(t)H^1 against the logarithm of β, resulting in a series of type curves characterized by different values of α. Matching of appropriately processed field data with the best-fit type curve allows estimation of aquifer transmissivity using a series of well-defined steps (e.g. Reference ButlerButler, 1997, p.58).
2.2.2. Guyonnet method
Since the Cooper–Bredehoeft model assumes that aquifers are unbounded, systematic deviations between observed slug-test responses and best-fit type curves often occur where flow boundaries exist within the portion of the aquifer influenced by slug tests (e.g. Reference Karasaki, Long and WitherspoonKarasaki and others, 1988; Reference Guyonnet, Mishra and McCord.Guyonnet and others, 1993). Subglacial aquifers at Alpine glaciers are notoriously heterogeneous (e.g. Reference Hubbard and NienowHubbard and Nienow, 1997), making the presence of flow boundaries within such portions likely. Constant-head and no-flow boundaries would, respectively, result in faster and slower WL recovery than predicted by the Cooper–Bredehoeft model (e.g. Reference Moench and HsiehMoench and Hsieh, 1985), representing a diagnostic means of their identification in a joint plot of observed response and best-fit type curve. Constant-head boundaries could be represented by water-filled subglacial channels or cavities, as discussed by Reference Iken, Fabri and FunkIken and others (1996) in a slug-test context, or by transitions from connected to unconnected regions of the glacier bed (section 1), which may hydraulically force each other (e.g. Reference Murray and ClarkeMurray and Clarke, 1995). No-flow boundaries could potentially result where subglacial sediment layers pinch off. Reference Guyonnet, Mishra and McCord.Guyonnet and others (1993) evaluate the analytical solution to the Cooper– Bredehoeft model (as summarized in Equations (3a–c)) to determine the distance between the tested borehole and constant-head or no-flow boundaries. The Guyonnet method thus promises to be well suited to identifying the nature and location of such boundaries in subglacial hydrological systems at Alpine glaciers.
Reference Guyonnet, Mishra and McCord.Guyonnet and others (1993) consider that any particular drawdown caused by a slug test will not travel beyond a certain distance (e.g. Reference SageevSageev, 1986), and focus on estimating this distance as a function of time, specifically allowing for storage in the test well, which may critically decrease the impact of a flow boundary on the response curve (e.g. Reference Karasaki, Long and WitherspoonKarasaki and others, 1988). Estimation of distance to the closest flow boundary uses a series of well-defined steps, based on a dimensionless formulation of the problem (Reference Guyonnet, Mishra and McCord.Guyonnet and others, 1993). Key to these steps are type curves representing functions of deviation between measured response curves and best-fit Cooper–Bredehoeft type curves, and of storage in the borehole.
2.3. High-transmissivity aquifers
Where the inertia of the borehole water column is significant, its momentum causes more water to flow into or out of the borehole face than is predicted by the Cooper– Bredehoeft model, generating oscillatory responses (e.g. Reference Bredehoeft, Cooper and PapadopulosBredehoeft and others, 1966). In this case, models based on the conservation of momentum are most adequate for the analysis of slug-test responses, where the displacement of borehole WL from static (w) can generally be expressed by (e.g. Reference ButlerButler, 1997, p. 153):
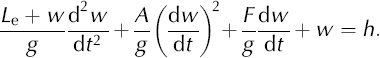
Here, Le is the effective length of the borehole water column plus some fraction of filter length (e.g. Reference ButlerButler, 1997, p. 153– 154), A is a parameter reflecting the significance of turbulence in the borehole (if A < 1, turbulence is of little significance;e.g. Reference Kabala, Pinder and MillyKabala and others, 1985), F is a viscous loss parameter, and g is the acceleration due to gravity. It is assumed that there is no initial velocity of the water surface in the well (dw/dt = 0 for t = 0) and that slug insertion or withdrawal is instantaneous (w(0) = H0). For a complete description of flow in a borehole–aquifer system induced by a slug test, Equation (4) must be coupled with a model such as Equation (1). According to Reference ButlerButler (1997, p. 154), there are two popular classes of linear high-transmissivity slug-test models. These are Van der Kamp type linear models and general linear methods (such as the Kipp method), both of which are considered in the present study.
2.3.1. Van der Kamp method
The Van der Kamp method connects a simplified version of Equation (4), ignoring the non-linear term, with Equation (1) to describe slug-induced flow in the borehole–aquifer system, thus being subject to their combined initial and boundary conditions. The damped-spring solution of classical physics is applied to the resulting governing equations. This solution is approximate, in that it is valid neither for the initial moments of the WL displacement (i.e. before the first sinusoid peak), nor for responses that are not well within the underdamped regime. If n is an index of iteration (n ≥ 1), this solution suggests that aquifer transmissivity (Tn) may be estimated from:
where
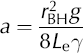
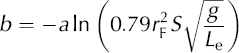
Equations (5a–d) use the notation of Reference Wylie and MagnusonWylie and Magnuson (1995), with ω and γ respectively representing the frequency and the damping constant of the induced WL oscillations. Reference Wylie and MagnusonWylie and Magnuson (1995) proposed a convenient spreadsheet approach for the implementation of the Van der Kamp method, which we adopt in the present study.
2.3.2. Kipp method
As outlined by Reference ButlerButler (1997, p. 159–163;a brief summary is presented here focusing on relevant aspects), general linear models have been developed to allow for any degree of damping, overcoming the limitations of the Van der Kamp method in this respect. Out of these, application of the type-curve approach included in the Kipp method has been particularly popular in field scenarios involving fully penetrating borehole filters. This approach conceptually considers the same analytical connection between flow in aquifer (i.e. using Equation (1)) and flow in the borehole (i.e. using an equivalent simplification of Equation (4)) as the Van der Kamp method, thus also being subject to their combined initial and boundary conditions. Suffice it to say that the key difference between the two methods is the mathematical solution to the simplified version of Equation (4), which in the Kipp approach allows for any degree of damping. This assumes that the magnitude of the dimensionless storage parameter (αK; Equation (6b)) is small, and that the value of the inertial parameter (βK Equations (6c and d)) is very large. The latter is related to the times of match between the measured response curve and the best-fit Kipp type curve through effective water-column length (Le). After Le, αK and βK have respectively been determined from Equations (6a), (6b) and (6c), the transmissivity (T) of the aquifer is estimated from Equation (6d):
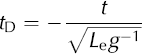
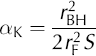

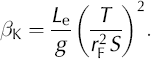
Here, tD is dimensionless time as used by the type curves, t is elapsed time of slug test, ζ is the damping factor and σ is a parameter expressing the significance of the borehole skin. Slug-test responses are respectively overdamped, critically damped and underdamped for ζ >1, ζ = 1 and ζ <1, and the Cooper-Bredehoeft solution applies for ζ > 5 where inertial effects become negligible (Reference KippKipp, 1985).
3. Field Site and Survey Protocol
3.1. Field site
Haut Glacier d’Arolla is a small valley glacier located at the head of Val d’Hérens, Valais, Switzerland (Fig. 2a). It has a surface area of ~6.3 km2 and extends from ~256O m a.s.l. at its snout to ~35OOm a.s.l. at its headwall (e.g. Reference RichardsRichards and others, 1996). The survey site considered in the present study is located in the eastern part of the ablation area (Fig. 2b), and is predominantly underlain by unconsolidated sediments (Reference Copland, Harbor and SharpCopland and others, 1997). A major melt-season drainage channel dominates subglacial water discharge in the survey area during the late melt season in August (e.g. Reference Hubbard, Sharp, Willis, Nielsen and SmartHubbard and others, 1995; Reference Gordon, Sharp, Hubbard, Smart, Ketterling and WillisGordon and others, 1998). This channel is located at the centre line of a variable pressure axis (VPA), which defines the spatial limits of hydraulic interaction between the channel and the surrounding, distributed subglacial drainage system (Fig. 2c, based on data collected by Reference Hubbard, Sharp, Willis, Nielsen and SmartHubbard and others (1995) in the 1993 melt season). Reference Hubbard, Sharp, Willis, Nielsen and SmartHubbard and others (1995) inferred that hydraulic interactions may extend to ~14Om transverse to channel orientation, causing systematic flushing of fines from the subglacial sediments. The latter was confirmed by Reference Kulessa and MurrayKulessa and others (2003) using electrical self-potential measurements, which indicated that clay minerals were largely absent in the channel area during the late melt season. The concept of subglacial erosion also agrees with the observation that sediment thickness (b SL) in this area increases from ~0.05 m near the subglacial channel to >0.2 m away from it (Reference Harbor, Sharp, Copland, Hubbard, Nienow and MairHarbor and others, 1997), which we must consider when converting transmissivity (T) to hydraulic conductivity (K). Flushing of fines was further suspected to lead to a gradual decrease in the hydraulic conductivity of the subglacial sediments away from the channel (Reference Hubbard, Sharp, Willis, Nielsen and SmartHubbard and others, 1995). We may evaluate this inference further, and estimate absolute values of hydraulic conductivity, using slug-test data collected in boreholes located at different distances from the channel (Fig. 2c). Some of our tested boreholes are located close to the channel (located at the centre line of the VPA in Fig. 2c), and the typical duration of a slug test is short compared to a diurnal water discharge cycle in the channel. The latter could therefore potentially act as a constant-head boundary during a slug test (section 2.2.2).

Fig. 2. Location of (a) Haut Glacier d’Arolla in Switzerland; (b) the section of the ablation area surveyed in 1994 and 1995; and (c) the boreholes used in these years. The location of the VPA in 1993 is also shown in (c). The channel is located at the centre line of the VPA, and direction of channelized water flow is from south to north.
3.2. Survey protocol
Boreholes were drilled using hot, pressurized water. Since drilling rates commonly vary and glacier ice is heterogeneous, non-uniform borehole radii often result. Filter radius may vary depending on the actual time the drill was halted at the base of the glacier, and on the properties of the subglacial material. We initially assume that borehole and filter radii have values of ~0.05 m and 0.25 m, respectively (Reference Iken, Fabri and FunkIken and others, 1996). It is, however, important to investigate the impact of potential variations in these parameters on our estimates of hydraulic conductivity and location of constant-head boundaries. We therefore calculate standard errors for reasonable ranges of borehole (0.03–0.07 m) and filter (0.05–0.25 m) radii, a practical approach to error analysis previously adopted by Reference Kulessa and MurrayKulessa and Murray (2003). The slug (a sealed pipe) was quickly inserted into, and subsequently quickly removed from, a borehole while recovery of the WL was monitored with a pressure transducer submerged in it. The transducer was connected to a Campbell Scientific CR10 data logger typically operated at 16 Hz, although in some cases the sampling rate was decreased to 0.2 Hz after the initial 30 s of the test, to save space on the logger. Each test was completed within a few minutes, allowing routine repetitive tests.
Slug tests conducted at Haut Glacier d’Arolla during the 1994 and 1995 melt seasons are identified in Table 1. All boreholes reported here were classified as fluctuating, and located along a transect established transverse to ice flow (Fig. 2c). Borehole labelling is such that the year of drilling is followed by the borehole number in that year. Twelve slug tests were conducted in 1994 in two fluctuating boreholes located near the subglacial channel detected in 1993 (e.g. Reference SharpSharp and others, 1993; Reference Hubbard, Sharp, Willis, Nielsen and SmartHubbard and others, 1995). In 1995, 12 slug tests were carried out in three boreholes spread over a comparatively large area (Table 1; Fig. 2c). All slug tests are labelled according to the type of displacement, borehole number, day of the year and time of test.
Table 1. Summary of 1994 and 1995 slug tests reported in this study. Borehole locations are illustrated in Figure 2c

4. Results
Underdamped responses were recorded in BH 94/69 and BH 94/75, while overdamped responses dominated in BH 95/1 and BH 95/14. Critical damping was observed in BH 95/16.
4.1. Underdamped responses
Typical slug-test responses recorded in BH 94/69 and BH 94/75 are presented in Figure 3. In the case of BH 94/69, initial displacement is just over 3 m, followed by an irregularly fluctuating WL. After a few seconds, the WL displacement begins to oscillate around the equilibrium WL, and eventually assumes its natural frequency. In BH 94/75, maximum WL displacements of just under 2 m are observed. Subsequent high-frequency oscillations are damped out after a few tens of seconds, merging into WL cycles characterized by the natural frequency of the coupled borehole–subglacial-aquifer flow system. The underdamped slug-test responses oscillate markedly longer than 1 min, and pre-displacement WLs are commonly established at the end of the tests. The other slug tests conducted in BH 94/69 and BH 94/75 (Table 1) yielded similar response signals.

Fig. 3. Typical underdamped slug-test responses recorded in (a) BH 94/69 and (b) BH 94/75. The grey lines indicate the pre-displacement WLs.
4.2. Overdamped responses
RHT 1/222/1814 (Fig. 4a) is representative of two falling-head and two rising-head tests conducted in BH 95/1. The test shown is characterized by high-frequency oscillations over the first 3 s, before establishing a pattern typical of an overdamped slug-test response. Maximum WL displacement is just over 1 m, recovering more rapidly (~30s) than the underdamped slug-test responses, which typically oscillated for >1 min (Fig. 3). Two falling-head and two rising-head tests were performed in BH 95/14 (Table 1). RHT 14/230/1531 (Fig. 4b) is characterized by exponential decays persistent over ~90s. Maximum WL displacements recorded in BH 95/14 are smaller (~0.8m) than those recorded in BH 95/1, but are persistent over a longer time period before the equilibrium WL is re-established (~80s).

Fig. 4. Typical overdamped slug-test responses recorded in (a) BH 95/1 and (b) BH 95/14. The grey lines indicate the pre-displacement WLs. Sampling interval was changed to 5s where black circles replace solid lines at later times.
4.3. Critically damped responses
RHT 16/224/1631 (Fig. 5) is representative of the four slug tests conducted in BH 95/16 (Table 1). After the first few seconds of the test, a relatively fast decay pattern is replaced by a slower WL rise lasting ~30s until the pre-displacement WL is re-established. The decay pattern is characteristically different from the overdamped and underdamped responses in that the initial WL recovery is relatively rapid, and only very slight, irregular WL fluctuations are observed at later times. This behaviour is typical of critical or at least nearcritical damping conditions.

Fig. 5. Typical slug-test response recorded in BH 95/16, suspected to be critically damped. The grey line indicates the predisplacement WL.
5. Interpretation
5.1. Evaluation of non-linear effects
We found that application of linear slug-test models to our data produced statistically significant fits between measured responses and calculated responses (underdamped case) or type curves (overdamped and critically damped cases). This provides an initial, diagnostic indicator that non-linear effects are most probably negligible (e.g. Reference ButlerButler, 1997; Reference McElweeMcElwee, 2001; Reference Kulessa and MurrayKulessa and Murray, 2003). Since Reference Stone, Clarke and EllisStone and others (1997) found that slug tests are generally unlikely to cause turbulence in subglacial aquifers, we are confident that non-linear effects in the aquifer beneath Haut Glacier d’Arolla are not of concern. Extensive sensitivity analyses conducted by Reference Stone and ClarkeStone and Clarke (1993) strongly suggested that slug-test induced turbulence in glacier boreholes is also negligible. However, in the present case, hydraulic heads were often larger (up to >100 m) than those reported by Reference Stone and ClarkeStone and Clarke (1993) (~50m or less), increasing the likelihood of turbulence occurring in the borehole during slug tests. In order to ascertain beyond doubt that the latter is not of concern, we have evaluated the magnitude of the non-linear parameter A in Equation (4) (Reference WilliamsonWilliamson, 2003). It was found to be of the order of 10–6 for both underdamped and overdamped responses, and 10–4 for those that were critically damped. Since turbulence in the borehole is negligible for A <1 (section 2.3), these findings indicate beyond reasonable doubt that such non-linearity may also be neglected, corroborating the findings of Reference Stone and ClarkeStone and Clarke (1993). We are therefore confident that slug-test induced turbulence in the entire borehole–subglacial flow system at Haut Glacier d’Arolla may be neglected, suggesting that application of linear slug-test models is correct.
5.2. Underdamped responses
5.2.1. Determination of subglacial transmissivity
Reference Stone, Clarke and EllisStone and others (1997) stressed the importance of removing non-slug-test related trends in WL from the response data. We use an approach similar to theirs, which involves fitting a straight line through and subsequently subtracting it from our data. In addition, the data prior to the first peak of WL displacement are removed from oscillating slug-test responses to satisfy the assumptions involved in the Van der Kamp model and the conditions of the approximate solution (Reference KraussKrauss, 1974; Reference Van der KampVan der Kamp, 1976).
Following data preparation, curve matching is employed to derive natural frequency and damping constant by least-squares minimization of the misfit between measured and calculated responses. The match between prepared field data and calculated oscillations is excellent (see example in Fig. 6) for all 12 underdamped slug tests analyzed. Entering natural frequency and damping constant into Equation (5) typically results in convergence after three iterations based on a tolerance of 0.1%. Effective water-column lengths are calculated to be ~90m and ~128m for BH 95/69 and BH 95/75, which, respectively, are in good and fair agreement with the observed pre-test WLs of ~85 m and ~111 m. Assuming a storage coefficient (S) of 1 × 10–4, which is a typical value for confined aquifers (Reference Freeze and CherryFreeze and Cherry, 1979, p.60), a borehole radius (rBH) of 0.05 m, and a filter radius (r F) of 0.25 m, we obtain transmissivity (T) estimates of 13.2 × 10–3m2s–1 for BH 94/69, and 5.7 × 10–3m2s–1 for BH 94/75.

Fig. 6. Application of the Van der Kamp method: matching of prepared field data (grey lines) and calculated oscillations (smooth black lines) for (a) BH 94/69 and (b) BH 94/75.
5.2.2. Sensitivity analysis
The transmissivities calculated in the previous section represent ‘best estimates’, assuming that (i) slug-test responses are perfectly repeatable, (ii) the least-squares fits between measured and calculated responses have a R2 of 1 and (iii) previously reported values of the storage coefficient (S) and borehole (rBH) and filter (rF) radius also apply at Haut Glacier d’Arolla. In practice, however, some errors normally arise when repeating slug tests and fitting calculated responses, and both radii and the storage coefficient could be somewhat different at Haut Glacier d’Arolla than at other glaciers. In order to investigate the effect of these uncertainties on our transmissivity estimates, we conduct sensitivity analysis using the approach suggested by Reference Kulessa and MurrayKulessa and Murray (2003). Each of the six uncertain parameters (response repeatability, oscillation frequency ω), damping constant (γ), borehole radius (rBH), filter radius (rF) and storage coefficient (S)) is assigned an error range within the limits of reason. Each parameter is then varied individually within its given error range relative to the best estimates of the other parameters. The resulting six transmissivity ranges are then used to calculate an overall standard deviation.
The resulting variations in transmissivity are summarized in Table 2. Response repeatability and curve-fitting errors have minor impact on transmissivity compared to variations in the other three parameters (Table 2). Of the latter, borehole radius (rBH) and the storage coefficient (S) have a particularly strong influence, causing transmissivity variations of almost one order of magnitude. Note that transmissivity is inversely related to filter radius (rF) and S. The standard deviation of the transmissivity range reported in Table 2 was calculated to be 5.2 × 10–3 m2 s–1 for BH 94/69 and 2.4 × 10–3 m2 s–1 for BH 94/75. We therefore conclude that the subglacial sediments at BH 94/69 and BH 94/75 have respective transmissivities of (13.2 ± 5.2 )x 10–3 m2 s–1 and (5.7 ± 2.4)x 10–3 m2 s–1.
Table 2. Results of sensitivity analysis for underdamped slug-test responses. Note that transmissivity is inversely related to filter radius (rF) and storage coefficient (S). Error ranges for repeatability and curve fits were different for each borehole and are not explicitly shown, to avoid overcrowding the table

5.3. Overdamped responses
5.3.1. Determination of subglacial transmissivity
The overdamped slug-test responses recorded in BH 95/1 and BH 95/14 were initially prepared in the same way as the underdamped responses (previous section), and subsequently fitted by exponential signal decays (e.g. Fig. 7a and b). During the first few seconds of a slug test, high-frequency fluctuations are often superimposed on the exponential decay (Reference Kulessa and HubbardKulessa and Hubbard, 1997). We ignore these fluctuations, in accordance with Reference Butler, McElwee and LiuButler and others (1996) who argued that such ‘fluctuations are related to test initiation and should be ignored when considering the quality of the match between the best-fit model and the test data’. All slug tests conducted in BH 95/1 produced a virtually identical match with the Cooper-Bredehoeft type curve for α = 10–10. This type curve presented the best-fit choice, yielding tC = 2.3 s for all four tests (Fig. 7c). With rBH = 0.05 m, a transmissivity (T) of 10.6 × 10–4m2s–1 is obtained. An analogous procedure applied to the responses recorded in BH 95/14 yields tC = 6.9s (Fig. 7d) and T = 3.6 × 10–4m2s–1 if rBH = 0.05 m. These calculated transmissivities are consistently lower than those inferred from analysis of underdamped slug-test responses recorded in BH 94/69 and BH 94/75 (Table 2).

Fig. 7. Application of the Cooper-Bredehoeft method: prepared field data (grey lines) and exponential decays (black lines) for (a) BH 95/1 and (b) BH 95/14, and logarithmically transformed exponential decays characterizing (c) BH 95/1 and (d) BH 95/14 (black lines) matched with the Cooper–Bredehoeft type curve for α = 10–10 (grey lines). tC is the time of match in the Cooper– Bredehoeft method, and t dev is the time of 1% deviation in the Guyonnet method. Sampling interval was changed to 5s where circles replace solid lines at later times in (a) and (b). Note that the abscissa label in (c) and (d) is equal to the dimensionless time parameter β (see Equation (3b)). W 0 is initial WL displacement.
5.3.2. Determination of subglacial constant-head boundaries
In this study, the later portions of all measured responses lie below the best-fit Cooper-Bredehoeft type curve, implying faster recovery (Fig. 7c and d) and, thus, the presence of a subglacial constant-head boundary (Reference Guyonnet, Mishra and McCord.Guyonnet and others, 1993). The presence of such boundaries is consistent with the inhomogeneous nature of the subglacial drainage system in the study area (section 3.1). Based on our best estimates of transmissivity (T = 10.6 × 10–4 m2 s–1 for BH 95/1 and 3.6 × 10–4 m2 s–1 for BH 95/14), storage coefficient (S = 1.0 × 10–4) and borehole radius (rBH = 0.05 m), we obtain respective distances of ~5m and ~6.5m from the bases of BH 95/1 and BH 95/14 to the closest constant-head boundaries (Fig. 8) using figure 6 in Reference Guyonnet, Mishra and McCord.Guyonnet and others (1993). Both values appear reasonable considering the limited radius of influence of the slug-test method in general, and the heterogeneous character of the subglacial drainage system in the survey area in particular. Reference Hubbard, Sharp, Willis, Nielsen and SmartHubbard and others (1995) located the centre of a subglacial channel at an easting of ~606785, and BH 95/1 is located at 606787.5 (i.e. 2.5 m from the channel;Fig. 2c). We therefore believe that the inferred constant-head boundary near this borehole is probably associated with this preferential water-flow pathway. The origin of the constant-head boundary near BH 95/14, and indeed its subglacial hydraulic connection as such, is probably related to preferential seepage induced by water entering the glacier bed near the eastern margin, where crevasses and surface streams are common.

Fig. 8. Determination of dimensionless distance from dimensionless time and the borehole storage coefficient (after Reference Guyonnet, Mishra and McCord.Guyonnet and others, 1993, fig. 6). The dashed and solid arrows, respectively, reflect application of the Guyonnet method in BH 95/1 and BH 95/14.
5.3.3. Sensitivity analysis I: transmissivity
Using the same approach to sensitivity analysis as that used in the underdamped case (section 5.2.2), we found that neither repeatability of the response signals nor variations in the initial amplitude of the exponential decays altered transmissivity noticeably. The sole parameter introducing major uncertainty is borehole radius (rBH), which may cause order-of-magnitude variations in transmissivity (Table 3). Together the transmissivity values listed in Table 3 produce a standard deviation of 3.7 × 10–4m2s–1 for BH 95/1 and 1.2 × 10–4m2s–1 for BH 95/14.
Table 3. Results of sensitivity analysis for overdamped and critically damped slug-test responses. Note that transmissivity is inversely related to filter radius (rF) in the Kipp case. Error ranges for curve fits were different for each borehole, and are not explicitly shown to avoid overcrowding the table

5.3.4. Sensitivity analysis II: distance to constant-head boundary
In the case of the Guyonnet method, uncertain parameters are (i) the time of 1% deviation between the exponential decay and the Cooper–Bredehoeft type curve (tdev), (ii) transmissivity (T), (iii) borehole radius (rBH) and (iv) the storage coefficient (Table 4). Uncertainty (i) is small for BH 95/1 and negligible for BH 95/14 (Table 4), which suggests that graphical estimation procedures are relatively accurate. Variations in transmissivity and borehole radius typically result in metre-scale variations of distance to the closest constant-head boundary (Table 4), which together with the small graphical uncertainties would place reasonable error bounds on distance to the closest constant-head boundary (1.0m for BH 95/1;1.5m for BH 95/14). However, unfortunately the storage coefficient has an overwhelming impact on this distance (Table 4). A storage coefficient of the order of 10–2–10–3, as previously reported for unfrozen marine sediments beneath Bakaninbreen, Svalbard (Reference Porter and MurrayPorter and Murray, 2001), produces an unrealistically small distance (^1 m). In contrast, a storage coefficient of the order of 10–7, as previously reported for Gornergletscher, Valais, Switzerland, based on slug tests (Reference Iken, Fabri and FunkIken and others, 1996), causes distance to reach 14.5m for both BH 95/1 and BH 95/14 (Table 4), which is not unrealistically large (e.g. Reference ButlerButler, 1997, p.183). Inclusion of the latter increases the standard deviation of the distance to the boundary to 2.9 m for BH 95/1, and 2.3 m for BH 95/14. Note that distance is inversely related to borehole radius (rвн) and the storage coefficient (S).
Table 4. Results of sensitivity analysis for Guyonnet method. Note that distance to constant head boundary (D) is inversely related to borehole radius (r BH) and storage coefficient (S)

5.3.5. Summary
Analysis of overdamped slug-test responses reveals that BH 95/1 is underlain by unconsolidated sediments that have a transmissivity of 10.6 ± 3.7 × 10–4m2s–1. The base of this borehole is located 5 ± 2.9 m from the closest subglacial constant-head boundary, which probably corresponds to the subglacial channel detected by previous authors (section 3.1). The sediments beneath BH 95/14 have a transmissivity of (3.6± 1.2)x 10–4m2s–1, and its base is located 6.5 ± 2.3 m from the closest constant-head boundary. The latter is probably associated with water entering the glacier bed at the eastern margin. It is unlikely that the subglacial storage coefficient (S) is larger than ~10–4 at either borehole since unrealistically small distances to constant-head boundaries would result.
5.4. Critically damped responses
5.4.1. Determination of subglacial transmissivity
The Kipp method promises to allow both identification of critically damped response signals, and estimation of subglacial hydraulic properties. Data are initially prepared in the same way as underdamped slug-test data (section 5.2.1). The match between all four repeat tests in BH 95/16 and the Kipp type curve for ζ = 1.5 is very good (Fig. 9). The test responses in this borehole are therefore just overdamped, although the Cooper–Bredehoeft solution does not apply since inertia is still significant (section 2.3.2). Using a filter radius (rF) of 0.25 m, a storage coefficient (S) of 1.0 × 10–4, and an effective water column length (Le) of 23.1 m as measured at the time of testing, Equation (6d) yields a transmissivity (T) of 4.7 × 10–3 m2s–1.

Fig. 9. Application of the Kipp method: matching of prepared field data (black circles) with the Kipp type curve for ζ = 1.5. W0 is initial WL displacement.
5.4.2. Sensitivity analysis
Similar to the overdamped case (section 5.3.3), repeat slug tests were found to produce negligible transmissivity variations (Table 3). Both borehole (rBH) and filter (rF) radii have an impact of up to approximately one order of magnitude on transmissivity estimates, transmissivity being inversely related to rF and the storage coefficient (S). Reducing the latter from 1.0 × 10–4 to 1.0 × 10–7 approximately doubled the transmissivity estimate, while the Kipp inertial parameter (/3K), and thus transmissivity (Equation (6d)), could not be calculated for S < 10–4 (Table 3). This agrees with previous conclusions based on application of the Guyonnet method to the overdamped slug-test responses (section 5.3.4), and therefore confirms that the subglacial storage coefficient is unlikely to be larger than this value.
We conclude that the sediments below the base of BH 95/16 have a transmissivity of (4.7 ± 4.0) x 10–3 m2 s–1, and that the subglacial storage coefficient (S) in our study area is probably of the order of 10–4 or smaller.
6. Synthesis of Subglacial Hydraulic Conditions
The estimates of transmissivity for the five boreholes considered in the present study are synthesized in Figure 10 together with inferred ranges of uncertainty. Transmissivities within the area of the 1993 VPA (boreholes 94/69, 94/75, 95/1 and 95/16) are enhanced compared to BH 95/14, which was located outside the VPA. This distribution of subglacial transmissivity supports the inferences of Reference Hubbard, Sharp, Willis, Nielsen and SmartHubbard and others (1995), who postulated that systematic flushing of fines is likely to decrease the water-flow resistance of the subglacial sediments located within the VPA compared to those located outside it (section 3.1).

Fig. 10. Subglacial drainage conditions transverse to ice-flow direction as inferred from slug tests. The location of the VPA in 1993 (see text) is also shown.
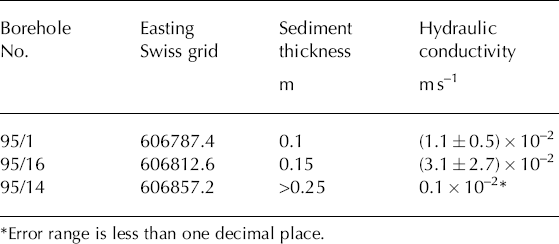
Previous field studies reported the ability of subglacial sediments to transmit water in terms of hydraulic conductivity (K) more often than transmissivity (T) (Table 5). Transmissivities obtained for boreholes 95/1, 95/16 and 95/14 were therefore converted to hydraulic conductivities using Reference Harbor, Sharp, Copland, Hubbard, Nienow and MairHarbor and others’ (1997) sediment thickness data collected in the 1995 melt season (we do not have sediment thickness estimates for boreholes 94/69 and 94/75). These authors found that sediment thickness near the location of BH 95/1 is close to the lower end of the inferred range (~0.1 m) and increases to values of ~0.26 m near BH 95/14. Table 6 summarizes the hydraulic conductivities (K) for these three boreholes, using an uncertainty range of (± 0.05 m for the estimates of sediment thickness. Hydraulic conductivity decreases by more than an order of magnitude from >1 × 10–2 m s–1 within the VPA (BH 95/1, BH 95/16) to 0. 1 × 10–2ms–1 outside the VPA (BH 95/14). These values fall within the range for clean sand according to Reference Freeze and CherryFreeze and Cherry (1979, p. 29), although overlap with other material ranges suggests the presence of gravelly sand within the VPA, and silty sand outside it. Nonetheless, it must be cautioned that slug tests are only successful in hydraulically well-connected boreholes, and by their very nature therefore sample only particularly transmissive areas of the glacier bed (e.g. Reference Stone, Clarke and EllisStone and others, 1997; Reference Kulessa and MurrayKulessa and Murray, 2003). It is therefore not possible to estimate the hydraulic conductivities of unconnected, less transmissive regions of the glacier bed using slug tests.
Table 5. Approximate hydraulic conductivities (K) of glacial till and unconsolidated subglacial sediments. Reference Freeze and CherryFreeze and Cherry (1979) did not specify methods of investigation

Table 6. Approximate range of hydraulic conductivity (K) in the eastern section of the survey area depending on best estimates of sediment thickness (bSL) beneath BH 95/1, BH 95/16 and BH 95/14
7. Conclusions
Using slug-test data collected in boreholes drilled through Haut Glacier d’Arolla, we have demonstrated that hydraulic properties of unconsolidated subglacial sediments can be estimated using conventional linear models that have been popular in groundwater studies for some time. Such models are more readily applied to such data than the interpretation techniques previously developed for hydro-glacial investigations. We initially demonstrated that slug tests are unlikely to induce turbulent flow in the coupled borehole–aquifer flow system, which confirms earlier findings by Reference Stone and ClarkeStone and Clarke (1993) and Reference Stone, Clarke and EllisStone and others (1997). We subsequently used the Van der Kamp (1985), Reference KippKipp (1985) and Cooper– Bredehoeft (Reference Cooper, Bredehoeft and PapadopulosCooper and others, 1967) methods to determine subglacial hydraulic properties from underdamped, critically damped and overdamped slug-test responses. Sensitivity analyses reveal that the repeatability of slug tests and the curve-fitting procedures involved in the three methods are less likely to generate significant errors in hydraulic estimates than geometrical and hydrological parameter uncertainties in the coupled borehole–subglacial flow system. This is particularly true for borehole radius and aquifer storage coefficient in the Van der Kamp case, borehole radius in the Cooper–Bredehoeft case and, most notably, filter radius in the Kipp case. We have further demonstrated that additional application of the Guyonnet method (Reference Guyonnet, Mishra and McCord.Guyonnet and others, 1993), which exploits systematic deviations between measured responses and Cooper–Bredehoeft type curves, is well suited to estimating the distance from tested boreholes to subglacial flow boundaries. The accuracy of the distance estimates was found to be ~3 m, being strongly sensitive to uncertainties in the aquifer storage coefficient. It is noteworthy that Reference Freeze and CherryFreeze and Cherry (1979, p. 60) argue that the storage coefficient for confined aquifers generally ranges between 5 × 10–3 and 5 × 10–5, which is a much smaller range than that used here for error estimation (10–2–10–7). We prefer to use the latter since these values were inferred from in situ borehole measurements at warm-based glaciers (Reference Iken, Fabri and FunkIken and others, 1996; Reference Porter and MurrayPorter and Murray, 2001), although the error estimates for the Van der Kamp and Guyonnet cases decrease noticeably if the smaller Reference Freeze and CherryFreeze and Cherry (1979) range is considered.
The key findings of this study regarding the subglacial hydraulic system at Haut Glacier d’Arolla are that the hydraulic conductivity of the unconsolidated subglacial sediments decreases from ~1–3 × 10–2 ms–1 (gravelly sand) near a subglacial channel to ~0.1 × 10–2ms–1 (silty sand) ~70m from it, and that inferred subglacial flow boundaries coincide with the subglacial channel. The storage coefficient of the subglacial sediments is probably of the order of 10–4 or smaller.
Acknowledgements
This work was funded by a University of Wales Postgraduate Studentship, which is gratefully acknowledged. Thanks to the numerous assistants who helped drill the boreholes and conduct the slug tests in the field. We also thank J. Walder, G. Flowers and an anonymous referee for their detailed comments on earlier versions of the manuscript.




















