1. Introduction
Reference Dyurgerov and MeierDyurgerov and Meier (2005) suggested that modern glaciers cover an area of 116 180 km2 in high-mountain Asia, among which more than half (52%) are in western China (Reference Shi, Liu, Wang, Liu and BaishengShi and others, 2005). These glaciers represent important water resources, contributing significantly to stream-flow. Glaciers exert a considerable influence on the hydrology of arid regions (by temporarily storing water as snow and ice on many different timescales) in western China and other parts of the globe where water resource is the key factor for the sustainable development of an ecological environment and human activities (Reference Yao, Liu, Pu, Shen and LuYao and others, 2004). Of particular interest to us is the timing and magnitude of meltwater fluxes from glaciers. To this end, during the past few decades, numerous models have been suggested and implemented to compute meltwater, ranging from those based on detailed evaluation of the surface energy fluxes (e.g. Reference Brun, Martin, Simon, Gendre and ColeouBrun and others, 1989; Reference AmbachArnold and others, 1996; Reference Brock and ArnoldBrock and Arnold, 2000) to those that use air temperature as the sole index of melt energy (e.g. Reference BraithwaiteBraithwaite, 1995; Reference HockHock, 1999).
In general, the surface energy balance determines glacier melt, but models based on energy flux are often problematic because the required data are unavailable. This is particularly true of glacierized areas in western China, where we have long-term observational data for very few glaciers. Consequently, application of degree-day models has been the most widely used method for both glaciological and hydrological purposes, due to their parsimony in data requirement compared with the energy-balance models (e.g. Reference TangbornTangborn, 1984; Reference Laumann and ReehLaumann and Reeh, 1993; Reference JóhannessonJóhannesson, 1997; Reference OerlemansOerlemans and others, 1998; Reference Braithwaite and ZhangBraithwaite and Zhang, 1999). Degree-day models simplify the suite of complex physical processes that are more properly described by the energy balance of the glacier surface and the overlaying atmospheric boundary layer. Such an approach was first used for an Alpine glacier by Reference Finsterwalder and SchunkFinsterwalder and Schunk (1887), and the approach was later refined (e.g. Reference Hoinkes and SteinackerHoinkes and Steinacker, 1975; Reference BraithwaiteBraithwaite, 1995; Reference HockHock, 1999). Despite their simplicity, the degree-day models have proven to be powerful tools for melt modelling, often on a catchment scale outperforming the energy-balance models (WMO, 1986).
In this paper we study Keqicar Baqi glacier, a large glacier in the southwestern Tien Shan, northwestern China. We first calculate glacier meltwater quantities at each elevation band on the glacier by applying a modified degree-day model, and additionally considering potential clear-sky direct solar radiation. Calculated meltwater and precipitation are then routed through the glacier via three parallel linear reservoirs. Second, we apply the model to evaluate the effect of a debris layer on the glacier meltwater and runoff, and to simulate the response of glacier runoff to different climate-change scenarios. This study forms part of ongoing studies of the glacier’s mass balance and geometrical changes, and the consequent impact on variations in water resources in the arid regions of northwestern China. Our aim is to provide a method for predicting glacier meltwater and runoff in glacierized areas, especially in remote high-mountain regions that are not routinely monitored. Such work is a necessary first step toward predicting the response of glacier runoff to future climate change in this poorly understood region.
2. Study Area And Data Collection
2.1. Study area
Keqicar Baqi glacier is a Turkistan glacier with length 26.0 km and total surface area 83.6 km2 (Fig. 1). It is located in the southwestern Tien Shan, northwestern China, ranging in altitude from ~3020 to ~6342 m a.s.l. The most striking characteristic of the glacier is a debris layer, which covers most of the ablation area (Fig. 2). The thickness of the debris layer generally varies from 0.0 to 2.5 m, although in some locations large rocks are piled up to several metres. Additionally, a subglacial drainage system is well developed in the melt season, so the residence time of meltwater is small (Reference Wang, Liu, Ding, Xie, Ding, Liu, Jiao, Wang and WangWang and others, 1987).

Fig. 1. Location of Keq¡car Baq¡ glacier in the southwestern Tien Shan, northwestern China.

Fig. 2. Hypsometric diagram of Keqicar Baqi glacier for debris- covered and debris-free surface conditions.
The climate on Keqicar Baqi glacier is affected mainly by westerly currents from the Atlantic and Arctic Oceans. During June to September 2003, the mean temperature at the glacier terminus (~3020 m a.s.l.) was 8.9°C, and generally the temperature on the glacier was above 0°C all day (Reference Zhang, Liu, Han, Wang, Xie and ShangguanZhang and others, 2004). The precipitation from May to September accounts for 70% of the total yearly precipitation in this region (Reference Wang, Liu, Ding, Xie, Ding, Liu, Jiao, Wang and WangWang and others, 1987).
2.2. Data collection
From June to September 2003, two automatic weather stations (AWSs) operated on the glacier (Fig. 1) at ~3100 and ~4300 m a.s.l. All sensors were sampled every 10 s, and data were stored as hourly averages. The stations were visited for maintenance at approximately 2 week intervals, depending on the weather conditions.
A total of 17 ablation stakes were drilled into the glacier at different elevations to monitor glacier melt (Fig. 1). Readings were taken regularly during AWS maintenance visits. Runoff was continuously monitored ~200m downstream from the glacier terminus at the principal stream (Fig. 1), using mechanical stage recorders, a pressure-type hydrological flow-meter and a hydrometric propeller.
The whole glacier was divided into elevation bands at intervals of 100 m, and the area of each elevation band was measured from a 90 m resolution digital elevation model derived from a heterogeneous dataset based on contour lines from existing maps. The area of debris-covered surface was derived from a Landsat Thematic Mapper image. The initial snow level (water equivalent) on the glacier was determined from the survey and ablation-stake readings. Initial snow cover on the surrounding valley slopes is difficult to quantify because measurements are restricted by the steepness of the terrain. At the beginning of the model simulation, the surrounding slopes and the ablation area were mostly snow- free. Any snow cover above the equilibrium-line altitude is taken into account.
3. Model Description
3.1. Glacier melt
Glacier melt is computed using a modified degree-day model which includes potential clear-sky direct solar radiation. This overcomes the shortcomings of the classical degree-day model with respect to the temporal resolution and the spatial variability of the melt rate. This approach is developed further by Reference HockHock (1999).
The daily depth of melt, M(i,t), in the ith elevation band on day t is given by
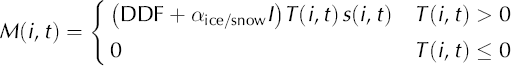
where DDF is the degree-day factor, α is a radiation coefficient which differs for snow and ice surfaces, I is the potential clear-sky direct radiation at the glacier surface, and T and s are daily mean air temperature and surface area, respectively, of each elevation band. There are three types of surface condition on Keqicar Baqi glacier: debris-free ice, debris-covered ice and snow; and the degree-day factor is different for each, due to the different thermal processes. Reference Zhang, Liu, Xie and DingZhang and others (2006b) suggested that monthly variations of degree-day factors are insignificant on Keqicar Baqi glacier. We therefore assume the degree-day factor is temporally and spatially constant within each elevation band. Air temperature is extrapolated to each elevation band using a vertical lapse rate of 0.006°Cm–1, derived as an average from the data at AWSs 1 and 2. The data recorded at AWS 1 (Fig. 1) are used as input.
Apart from temperature, no additional time-dependent meteorological variables are required. Potential clear-sky direct radiation, I, is calculated as a function of top-of- atmosphere solar radiation from assumed atmospheric transmissivity, solar geometry and topographic characteristics (Reference Garnier and OhmuraGarnier and Ohmura, 1968):
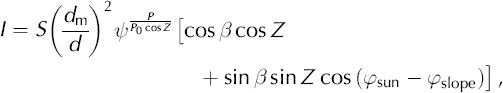
where S = 1360 Wm–2 is the solar constant (Reference Peixoto and OortPeixoto and Oort, 1992), (dm/d)2 is the eccentricity correction factor for the Earth’s orbit (Reference Peixoto and OortPeixoto and Oort, 1992), is the mean atmospheric clear-sky transmissivity, varying from 0.6 to 0.9 (Reference OkeOke, 1987), P is the atmospheric pressure, P0 is the mean atmospheric pressure at sea level, Z is the zenith angle, which is approximated as a function of latitude, solar declination and hour angle (Reference Peixoto and OortPeixoto and Oort, 1992), ß is the slope angle, φsun is the solar azimuth angle and φslope is the slope azimuth angle.
3.2. Precipitation
Precipitation is distributed to each elevation band as a function of elevation, and assumed to increase linearly by 8.8% over the elevation range (3020–6342 m a.s.l.) of the glacier (Reference Zhang, Liu, Xie and DingZhang and others, 2006a). Snow and rainfall are discriminated according to a temperature divider of 1.5°C. Observed precipitation contains undercatch errors including dynamic loss, evaporation loss and wetting loss (Reference Yang, Shi, Kang and ZhangYang and others, 1989). According to field observations and experiments in Tien Shan, the rain- and snow-correction factors are 1.1 and 1.3, respectively (Reference Yang, Shi, Kang and ZhangYang and others, 1989).
3.3. Runoff routing
Sums of meltwater and rainfall are transformed into runoff using a linear reservoir model based on Reference Baker, Escher-Vetter, Moser, Oerter and ReinwarthBaker and others (1982). The runoff-routing model has been applied to glaciers in different regions (e.g. Reference HockHock, 1999; Reference Escher-VetterEscher-Vetter, 2000; Reference Klok, Jasper, Roelofsma, Gurtz and BadouxKlok and others, 2001). In this model a glacier is subdivided into three reservoirs, one each for firn, snow and ice, corresponding to their different hydraulic properties (Reference Baker, Escher-Vetter, Moser, Oerter and ReinwarthBaker and others, 1982). The firn reservoir is defined as the area above the previous year’s equilibrium line. The ice reservoir includes the area of debris-covered ice and debris- free ice, and the snow reservoir refers to the snow-covered area outside the firn reservoir.
The linear reservoir volume, V(t), is proportional to its runoff, Q(t), the factor of proportionality being the storage constant, k, with time units. Storage and continuity equations for the reservoir are given by
where R(t) is the rate of water inflow to the reservoir, here equivalent to the sum of meltwater and rainwater. Combining Equations (3) and (4) yields
For daily time intervals, the runoff, Q, is given by
3.4. Model testing and parameter optimization
Glacier meltwater and runoff are simulated for the period 1 July to 12 September 2003. The performance of the model is assessed by the agreement between modelled and measured meltwater at the ablation stakes and the agreement between computed and observed runoff hydrographs. The agreement with respect to runoff is expressed in terms of Nash–Sutcliffe efficiency (NSE) and square-root Nash– Sutcliffe efficiency (NSE.SQRT).
Nash–Sutcliffe efficiency has been widely used for the assessment of model performance, often as the sole criterion (e.g. Reference GottliebGottlieb, 1980; Reference Wilcox, Rawls, Brakensiek and WrightWilcox and others, 1990; Reference HockHock, 1999; Reference Zappa, Pos, Strasser, Warmerdam and GurtzZappa and others, 2003), and is given by (Reference Nash and SutcliffeNash and Sutcliffe, 1970)
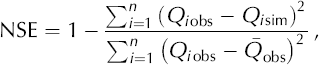
where Q is glacier runoff, the subscripts ‘obs’ and ‘sim’ denoting observed and simulated, respectively. The bar indicates the mean and n the number of time-steps calculated. Because of non-constant variance of model errors, this criterion tends to emphasize large errors, i.e. those generally occurring during flood events. A more all-purpose criterion is obtained using square-root of the runoff, given by (Reference Perrin, Michel and AndreassianPerrin and others, 2001)
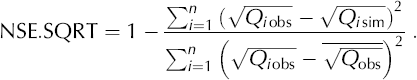
These criteria give a value of 1 in the case of perfect agreement. In this study, NSE and NSE.SQRT are applied to evaluate the model performance both in calibration and validation. Calibration is conducted using the observed data from 1 July to 31 July 2003, and validation from 1 August to 12 September 2003.
To assess the performance of meltwater simulations, relative error (RE) and relative standard deviation (RSD) are employed. These are based on the differences between simulated meltwater, Msim, and observed meltwater, Mobs, at each ablation stake on the glacier, defined as:
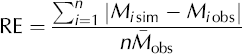

where the bar indicates the mean and n the number of ablation stakes.
The numerical criteria defined in Equations (7–10) are also used to optimize the model parameters DDF, αice/snowand k (Equations (1) and (5)). Optimization is achieved by varying the parameters until optimal agreement between simulations and observations is obtained. The July 2003 data are used for optimization. The parameters obtained are then applied to the August and September 2003 dataset without alteration. Optimization involves two steps. First, the agreement between simulated and observed runoff is maximized. Second, the ablation measurements are used to constrain the parameters. Both parameters are allowed to vary over a wide range of values, and the parameters associated with the best agreement achieved both between modelled and measured melt and between simulated and observed runoff are chosen. Optimized parameters are given in Table 1.
Table 1. Optimized parameters (degree-day factor (DDF), storage constant (k) and radiation coefficient (α)) for the models

4. Results
4.1. Glacier meltwater and runoff
Modelled meltwater equivalent at ablation stakes was accumulated over the period 1 July to 12 September 2003, and compared with measured values (Fig. 3). Considering the simplicity of the model, simulations are in good agreement with observations (Fig. 3;Table 2), although some points lie away from a line with slope 1. This error may be attributed to the different weather characteristics of the optimization and the verification months;July 2003 exhibited mainly rainy and overcast conditions, while in September 2003 the weather was mainly dry and sunny. The degree-day factor varies according to the relative contributions of the energy- balance components (Reference AmbachAmbach, 1988), and their relative importance varies with weather conditions.
Table 2. Results of the meltwater and runoff simulations of Keqicar Baqi glacier, expressing the agreement in terms of NSE, NSE.SQRT, Model parameter Optimized value RE and RSD, which are defined in Equations (7–10)
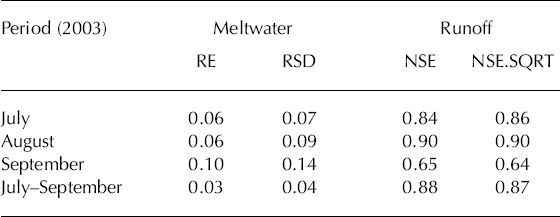

Fig. 3. Modelled and measured glacier meltwater on Keqicar Baqi glacier for the period 1 July to 12 September 2003.
Glacier runoff is computed from meltwater and rainwater for the period 1 July to 12 September 2003. Simulated and observed runoff hydrographs are given in Figure 4, which indicates there is good agreement between simulated and observed runoff. NSE and NSE.SQRT values through the study period were 0.88 and 0.87, respectively (Table 2). Total runoff is underestimated by 8.0% during the study period. While the timing and the amplitudes of runoff cycles may be well modelled, peak flows tend to be overestimated (Fig. 4). This may be because (i) meltwater or precipitation may have been overestimated or (ii) the debris layer that covers most of the ablation area has a strong effect on the glacier meltwater and runoff.

Fig. 4. Observed and simulated runoff (mm), precipitation P (mm) and air temperature T(°C) at AWS 1 on Keqicar Baqi glacier for the period 1 July to 12 September 2003.
4.2. Effect of the debris layer
A thick supraglacial debris layer covers ~60°% of the ablation area of Keqicar Baqi glacier (Fig. 2). The thermal processes on the debris layer are quite different from those on bare ice or snow (Reference ØstremØstrem, 1959; Reference Rana, Nakawo, Fukushima and AgetaRana and others, 1997). The main physical characteristics of the debris layer are the thermal conductivity and albedo that control heat conduction to the ice–debris interface. Reference ØstremØstrem (1959) suggested that, if the debris layer is thinner than a threshold value of about 30 mm, glacier melt under the debris layer is greater than that on bare ice, while if the layer is thicker than the threshold value, melt is less. An experiment was carried out on the ablation area of Keqicar Baqi glacier over the period 25 June to 10 August 2003. Three different sites were chosen, with debris thicknesses of ~80, ~150 and ~210mm. Theoretical calculations of heat transfer indicate there should be a considerable difference in energy supplied to the base of the debris layer in these three cases, 26.9, 9.8 and 6.9 Wm–2, respectively (Han and others, 2005). It is seen that it is vitally important for modelling glacier runoff that the effect of the debris layer on glacier meltwater during the study period be evaluated. This is the main reason that the degree-day factor for the debris-covered ice is less than for the debris-free ice.
To evaluate the effect of the debris layer on glacier meltwater and runoff during the study period, these parameters were recomputed using Equations (1–6) assuming an entirely debris-free surface on Keqicar Baqi glacier. The model output was then compared with model runs with the actual surface debris cover. The distribution of meltwater with altitude shows the strongest melt in the 3600– 3900ma.s.l. elevation band rather than at the glacier terminus. Indeed, meltwater generation decreases markedly as debris thickness increases (Fig. 5). Comparing the computations with debris to those without debris, glacier meltwater with the true surface condition is markedly reduced (cf. the debris-free surface) below the elevation band of 4000 m a.s.l. (Fig. 5). Figure 6 shows the variation of cumulative runoff calculated with the true surface condition and with the assumed debris-free surface. The results predict a 35% increase of glacier runoff during the study period due to the debris on Keqicar Baqi glacier. It is apparent that the insulation effect of the debris layer is significant and plays an important role in glacier meltwater generation and runoff.

Fig. 5. Distribution of glacier meltwater with altitude, showing both the debris-covered surface and the assumed debris-free surface on Keqicar Baqi glacier.

Fig. 6. Variation of cumulative runoff calculated showing both the debris-covered surface and the assumed debris-free surface.
4.3. Climate change and glacier runoff
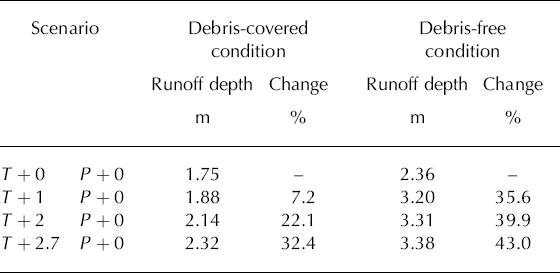
The global average surface temperature is projected to increase by 1.4–5.8°C in the coming decades due to anthropogenically induced greenhouse warming. Measurements of land-surface precipitation indicate an increase of 0.5–1% per decade throughout the mid- and high latitudes of the Northern Hemisphere (Reference FollandFolland, 2001). For northwestern China, the ReCM2 regional climate model (RCM), nested within a global coupled ocean–atmosphere climate model (CSIRO R21L9 AOGCM), provides better simulations of surface air temperature and (especially) precipitation than the CSIRO model (Reference Gao, Zhao, Ding, Huang and FilippoGao and others, 2001). The ReCM2 model has a horizontal resolution of 60 km x 60 km and has 16 vertical layers. Projected results indicate that the average temperature will increase by 2.7°C and precipitation will increase by 25% in the coming decades given a doubling of the CO2 (Reference Gao, Zao and DingGao and others, 2003).
We adopt this scenario to analyze the response of glacier runoff to climate change in the coming decades on Keqicar Baqi glacier. The adopted changes in temperature and precipitation range from 0 to 2.7°C and from 0 to 25%, respectively, and the effect of the debris layer on glacier runoff is taken into consideration. Assuming the temperature increases with unaltered precipitation conditions, glacier runoff will initially increase due to release of water. However, prolonged long-term mass loss will reduce glacier volume, which in turn will lead to reduced water yields (Reference Jansson, Hock and SchneiderJansson and others, 2003). Keqicar Baqi glacier has generally experienced a retreat and thinning since the 1980s in response to a ~0.7°C increase in mean temperature in northwestern China (Reference Wang, Liu, Ding, Xie, Ding, Liu, Jiao, Wang and WangWang and others, 1987; Reference Chen, Takeuchi, Xu, Chen and XuChen and others, 2006). Therefore, the area change of Keqicar Baqi glacier in the coming decades is considered in the simulation process.
The effects of different climate-change scenarios on daily glacier runoff are shown in Figures 7 and 8. Figure 7 shows results where the debris cover has been considered. Figure 8 shows results assuming no debris cover. Figures 7a and 8a show results of model runs in which glacier area and precipitation are unchanged while temperature is increased by 0, 1, 2 and 2.7°C. Figures 7b and 8b show results in which glacier area is unchanged and temperature is held to an increase of 2.7°C while precipitation is increased by 0, 10, 20 and 25%. Figures 7c and 8c show results in which temperature is held to an increase of 2.7°C and precipitation is unchanged, while glacier area is reduced by 0 and 50%, and in which precipitation is increased by 25% while glacier area is reduced by 50%.

Fig. 7. Effects of increased temperature and precipitation and reduced glacier area on glacier runoff at Keqicar Baqí Glacier. Units of temperature and runoff depth are °C and m, respectively.

Fig. 8. Effects of increased temperature and precipitation and reduced glacier area on glacier runoff at Keqicar Baqi glacier with a debris-free surface assumed. Units of temperature and runoff depth are °C and m, respectively.
From Figure 7a, there is a dramatic increase in glacier runoff with increasing temperature, expected because the total glacier area and precipitation are kept constant. Higher runoff is predicted whether or not the debris- covered surface condition is taken into consideration (Figs 7a and 8a; Tables 3 and 4). The response of glacier runoff with the debris-covered surface condition is relatively less sensitive to the increase of temperature than that with the assumed debris-free surface condition (Figs 7a and 8a; Tables 3 and 4). This indicates that the debris layer covering most of the ablation area plays an important role in the melt process and protects the glacier from much more rapid mass loss.
Table 3. Effect of temperature increase on glacier runoff with the debris-covered surface condition and with a debris-free surface condition. Units of temperature (T) and precipitation (P) change are °C and %
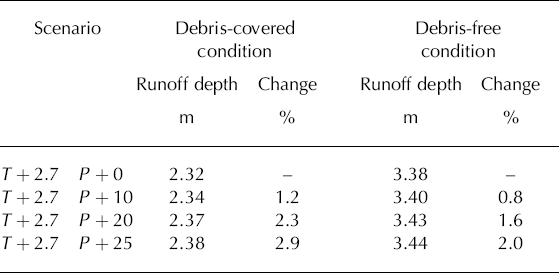
From Figures 7b and 8b, it is seen that there is less significant increase in glacier runoff with the increase in precipitation from 0 to 25% with the unaltered temperature conditions whether or not the debris-covered surface condition is taken into account (Table 4).
Table 4. Effect of precipitation increase on glacier runoff given a temperature increase of 2.7°C with the debris-covered surface condition and with a debris-free surface condition. Units of temperature (T) and precipitation (P) change are °C and %
From Figures 7c and 8c, there is a reduction in glacier runoff when a markedly reduced glacier area is prescribed assuming unaltered temperature conditions whether the debris-covered surface condition is taken into account or not.
5. Conclusions
A modified degree-day model including potential clear-sky direct solar radiation is applied to Keqicar Baqi glacier. The model includes a distinct spatial element by including the potential clear-sky direct solar radiation. Thus the effects of topography on glacier melt are accounted for. Although glacier melt is determined by the surface energy balance, this model is especially suitable for applications on many types of glaciers where there is a lack of sufficiently detailed energy component data. Air temperatures can readily be recorded by standard meteorological stations or, when required in remote glacierized areas such as western China where very few observational data exist, generated by GCM (Global Climate Model).
The model performs well with respect to both glacier meltwater and runoff. Expressing the agreement between simulated and observed runoff in terms of NSE and NSE.SQRT criteria, values of 0.88 and 0.87 are obtained for the period 1 July to 12 September 2003. The reconstruction of glacier meltwater and runoff during the study period indicates that below 4000 m a.s.l. glacier meltwater generation would increase dramatically if there were an entirely debris-free surface. Total glacier runoff would be increased by ~35%. Climate scenarios are adopted based on simulations of ReCM2 RCM in a doubling of CO2 scenario for Keqicar Baqi glacier. The adopted changes in temperature and precipitation range from 0 to 2.7°C and from 0 to 25%, respectively. Results indicate that glacier runoff increases linearly with temperature as the latter increases from 0 to 2.7°C, whether the debris-covered surface condition is taken into account or not. A less significant increase in runoff is evident with increasing precipitation. Glacier runoff is dramatically reduced with glacier area reducing by 50% in the +2.7°C scenario.
It is necessary to be aware of the limitations of our calculation method. In this study, the degree-day factors are assumed constant in space and time. There are some uncertainties in the degree-day factors linking snow- or ice melt to temperature on the glacier. In addition, there is uncertainty in the extrapolated air temperature at different elevation bands of the glacier using the vertical lapse rate. Finally, the spatial distribution of precipitation represents an important source of uncertainty. Consequently, this model needs further refinement and development.
Acknowledgements
We thank two anonymous reviewers, the scientific editor B. Hubbard and the chief scientific editor T.H. Jacka for helpful comments and suggestions, which considerably improved the final manuscript. This work was financially supported by Chinese National Fundamental Research Program (Grants 40371026, 40571034, 40501007 and 90202013), the Knowledge Innovation Project of the Chinese Academy of Sciences (Grants KZCX2-YW-301 and KZCX3-SW-345) and the Cold and Arid Regions Environmental and Engineering Research Institute, Chinese Academy of Sciences (Grant 2004102).
















