1. Introduction
Entrainment in snow avalanches is the key to understanding the motion of snow masses and hence to predicting their speed, impact pressures and final runout distance (Reference IsslerIssler, 1998; Reference Gauer and IsslerGauer and Issler, 2004). Recently, different avalanche-entrainment mechanisms and rates have been reported by Reference Sovilla, Burlando and BarteltSovilla and others (2006), who analyzed a total of 18 avalanche events, many captured at the instrumented Vallée de la Sionne (Switzerland) test site. In this excellent and valuable survey of snow entrainment, three different entrainment mechanisms were identified: ploughing, step entrainment and basal erosion. The maximum entrainment rates (350 kg m−2 s−1) were found to occur during frontal ploughing and step entrainment. Although the step-entrainment mechanism was observed to occur by a fracture failure at the interface of two snow layers, the multilayer-entrainment model introduced by Reference Sovilla, Burlando and BarteltSovilla and others (2006) assumes that entrainment processes are governed by snow strength, primarily the shear resistance of snow. The entrainment model of Reference Sovilla, Burlando and BarteltSovilla and others (2006) is based on the earlier work of Russian snow scientists (Reference Grigorian, Eglit and YakimovGrigorian and others, 1967; Reference Eglit and DemidovEglit and Demidov, 2005). Although this model provides correct entrainment rates, it requires shear strength values with no clear physical basis.
In the following, we use the invariant Γ integral of fracture mechanics (see Reference CherepanovCherepanov, 1979) for the calculation of energy balance, frontal pressure and frontal resistance to the motion of the avalanche by the snowpack. We seek a method to model the step-entrainment process identified by Reference Sovilla, Margreth and BarteltSovilla and others (2007). The frontal resistance is calculated, which allows us to find the necessary condition governing the entrainment regime. For the start of avalanches, a limiting equilibrium condition equation is also found. Then the governing equation for the dynamics of avalanches is derived in the simplest approach, taking into account entrainment, inertia, gravitation and friction forces using the Voellmy–Salm model (Reference Bartelt, Salm and GruberBartelt and others, 1999). These governing equations are solved numerically and the Vallée de la Sionne avalanche of 7 February 2003 is simulated.
2. Frontal Resistance in the Fracture-Entrainment Mode
The frontal resistance due to entrainment is calculated assuming a multilayer snowpack. Slip fractures at the layer interfaces in the process zone are assumed to govern the resistance (Fig. 1). The energy balance of forces in this zone is given by means of the invariant Γ integral of fracture mechanics (Reference CherepanovCherepanov, 1979). The avalanche is assumed to move in the direction of the x 1 axis, with the x 2 axis being perpendicular. The x 3 axis is perpendicular to both the x 1 and x 2 axes.

Fig. 1. Integration contour, Σ, of the invariant Γ integral over the process zone based on the modified SBB (Sovilla–Burlando–Bartelt) fracture-entrainment model. Interface slips along the boundaries of adjacent layers. Closed Σ contour embraces the process zone, the direction of integration being shown by arrows.
Figure 1 represents a schematic snapshot of the process zone at a certain moment in time. The frontal resistance is a result of interactive stresses and strains in the process zone and can be calculated from the energy balance in this zone. For the purpose of such a calculation we make the following assumptions for the process zone:
-
1. The bed is an elastic continuum half-space, x 2 < 0, with one slip fracture along the interface boundary x 2 = 0 (Fig. 1).
-
2. Snow in front of the avalanche is a multilayer continuum with several boundaries along x 2 = constant being subject to slip fractures (Fig. 1). Inertial forces in the process zone are small in comparison to the fracture resistance.
-
3. All dissipative processes in the process zone are assumed to be concentrated along several slip discontinuities on interfaces at x 2 = constant, so the material outside of these discontinuities (fractures) is an elastic continuum.
-
4. The front of the snowpack is a solid line along x 1 = constant where the constant is different for different layers (Fig. 1). The shear stress on the front is zero, and the normal stress, σ 11, which is the frontal avalanche pressure of snow, is equal to
(1)
where h is the thickness of the resting snow layer in front of the snowpack and R F is the frontal resistance to be found from the energy conservation law.
-
5. Plane strain is assumed.
The dissipative processes on slip discontinuities, including their ends, are taken into account in Figure 1 by the paths over the upper and lower banks of discontinuities with small circular paths surrounding the ends of discontinuities. These circular paths are necessary since it is not known what happens with the material at the extreme ends under high stresses and strains in very small volumes. We can only characterize the dissipative process inside a small circular zone by a specific dissipation energy, spent to advance the discontinuity of unit length. Thus, the snow cover in the process zone is subject to comparatively small deformations up to failure, with both elastic and inelastic components produced by the front pressure of the avalanche. The law of energy conservation in a solid continuum inside a closed contour can be written in the form of the invariant Γ integral (Reference CherepanovCherepanov, 1979) taken over the closed contour, Σ, embracing the process zone with discontinuities (Fig. 1):
(i,j = 1,2; summation on repeated indices is assumed here), where W is the volume density of deformation work, nj are the components of the outer unit normal to contour Σ, σij are the stress components and ui are the displacement components.
The integral over the upper surface of snow layer, x 2 = h, is equal to zero because n 1 = 0, n 2 = 1 and σijjnj = 0 for i = 1, 2, since there is no loading on the free surface.
The integration path in the bed can be taken in the form of a circle of large radius, r, where r ≫ h. The stress–strain field in the bed far from the process zone tends to that of concentrated force (R F, 0). The Γ integral over this circle represents the Γ residue of the concentrated force, and it is equal to zero in this case (Reference CherepanovCherepanov, 1983).
The Γ integral over the front of the snowpack where x 1 = constant, n 1 = 1, n 2 = 0, σ 12 = 0 and σ 11 = R F/h is equal to
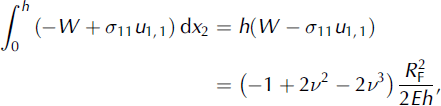
where E is Young’s modulus or modulus of elasticity and v is the Poisson ratio. From Hooke’s law, (plane strain) it follows that
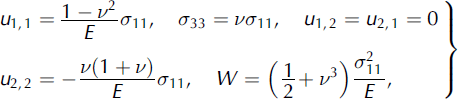
since σ 22 = 0 in the common thin-plate approximation as applied to the snow layer.
Now, let us calculate the Γ integrals over the slip discontinuities along x
2 = constant where: (1) n
1 = 0 and n
2 = ±1 (‘plus’ for the upper bank and ‘minus’for the lower bank); (2) σ
22 = 0 in the thin-plate approximation and (3) σ
12 = τi
,i + 1. Here, τi
,i + 1 is the limiting shear stress on the slip discontinuity between the ith and (i + 1)th layers. The Γ integral over the upper and lower banks of the ith discontinuity is equal to Δ
iτi
,i + 1, where ![]() is the summary displacement jump between the upper and lower banks of the discontinuity accumulated at the front of the snowpack, the so-called transverse shear crack distortion. Here Li
is the length of the ith discontinuity.
is the summary displacement jump between the upper and lower banks of the discontinuity accumulated at the front of the snowpack, the so-called transverse shear crack distortion. Here Li
is the length of the ith discontinuity.
The Γ integral over the small circular path surrounding the singular end of the ith discontinuity is equal to Γci , where Γci is the dissipation energy spent to increase the ith discontinuity by a unit length.
Combining these particular calculations in Equation (2) gives
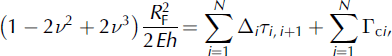
where N is the number of discontinuities. In the our case, we have N = 3.
Equation (5) allows us to formulate the frontal resistance, R F, in terms of h and structural material constants as follows:
where
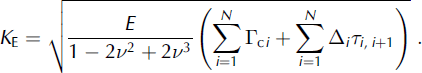
For the case of identical limiting shear stresses, with τi ,i + 1 = τ s for any i, we get

where ![]() is the summary shear displacement in the process zone near the front of the snowpack.
is the summary shear displacement in the process zone near the front of the snowpack.
The parameter K E is termed the entrainment toughness and characterizes the resistance capabilities of the material in the process zone in front of the avalanche. The determination of this value from actual avalanche data is required to predict avalanche motion with entrainment. According to Equation (7), the fracture work lost by an avalanche on a unit length of its path can be expressed in terms of the entrainment toughness as follows:
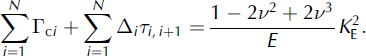
This formula describes the arresting capabilities of the process zone in front of the avalanche.
3. The Fracture-Entrainment Threshold
The fracture-entrainment mechanism described in the preceding section will occur if the force applied by the avalanche (which is also the resisting force of the snow-pack, R F) is the smallest of all possible entrainment mechanisms. Moreover, the fracture-mechanics based R F must be the smallest of all possible snow-cover resisting forces. Another possible entrainment mechanism is the shearing of interfaces between snow layers. To determine the resisting force of this process, first let us study the limiting equilibrium of the ith snow layer with a through slip plane CD inclined by angle βi to the x 1 axis (Fig. 2). The tangential (shear), τ n, and normal components of stress, σ n, on this interfacial slip plane obey Coulomb’s law
where τi is the adhesion constant and φi is the angle of internal friction in the ith layer. Values of τi and φi for snow avalanches derived from chute experiments can be found in Reference Platzer, Bartelt and KernPlatzer and others (2007). As σ 22 = 0 in the thin-plate approximation, we have the following two equations of equilibrium:
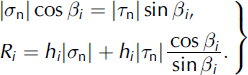
Here, hi is the thickness of the ith layer and Ri is the component of the frontal resistance caused by the ith layer.

Fig. 2. The non-entrainment mode of frontal resistance in the SBB multilayer model. Through slips AB, CD, EF and GH and interface slips BC, DE and FG along the boundaries of layers.
Solving the equation system, Equations (10) and (11), gives
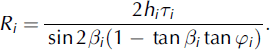
Let us analyze Ri
as a function of βi
. This function tends to plus infinity when βi
→ 0+ and ![]() . Hence, it has a minimum in
. Hence, it has a minimum in ![]() . Equating the derivative to zero, we find the following equation for the minimum point:
. Equating the derivative to zero, we find the following equation for the minimum point:
From here and Equation (13), it follows that
Summing up the resistance of all N layers, we arrive at the frontal resistance, ![]() , of the process zone
, of the process zone
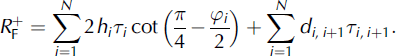
Here τi ,i + 1 is the limiting shear stress on the boundary between the ith and (i + 1)th layers, and di ,i + 1 is the length of the interface slip between the ith and (i + 1)th layers.
All terms in the second sum are positive; they increase the value of frontal resistance. Hence, di ,i + 1 = 0 for any i, and the absolute minimum with respect to all βi where i = 1, 2, …, N provides the frontal resistance, R F, of the process zone in the non-entrainment mode as follows:

If this value is less than that given by Equation (6) for the fracture-entrainment mode, then shearing entrainment is the more likely entrainment mode.
Therefore, fracture entrainment occurs if, and only if,

Equation (19) provides an important estimate for the upper bound of the entrainment toughness, K E, characterizing the frontal pressure and frontal resistance to the avalanche snowpack.
4. Estimates of Arresting Capabilities of Entrainment
Let us use Equations (9) and (19) to estimate the arresting power of the entrainment processes.
First, for a simple estimate, we assume i = 1, h = 1 m. Because of the great diversity of snow properties the cohesion constant, τi , can vary from 1 to ∼100 kPa, and the friction angle, φi , from 10° to 40°. From Equation (19) we find that the entrainment toughness, K E, can vary from 0.01 to 10 MPa m1/2.
Young’s modulus, E, of snow can vary from 0.01 to ∼1.0 GPa depending on the snow type and density. Using this range of values of E for snow and the above estimate of the entrainment toughness, K E, we find that the specific dissipation energy of entrainment per unit area according to Equation (9) can vary from 0.01 J m−2 to ∼10 MJ m−2, a very large range.
Let us compare this value with the work done by gravity per unit area which is MgH/A, where MgH is the potential energy of gravitation of avalanche mass M, H is the total mountain height and A is the total area covered by the moving snow mass. Using data from Reference Sovilla, Burlando and BarteltSovilla and others (2006), the following estimates are acceptable for avalanches: M varies from 0.01 × 106 to 0.1 × 106 kg and A varies from 0.1 to ∼1 km2. If we assume that H = 1000 m, then the specific driving force of avalanches will vary from 0.1 to ∼10 MJ m−2.
As seen, under common snow conditions the dissipation energy of entrainment is considerably less than the work done by gravity. However, the specific dissipation energy of entrainment of a well-consolidated snow cover is comparable with the gravitational work done by an avalanche. A similar result was obtained by Reference Bartelt and StöckliBartelt and Stöckli (2001) for the entrainment of woody debris by avalanches.
5. Numerical Model: Frictional Resistance with Entrainment
A mountain of height H is covered by a layer of snow. We designate t as time; x as the vertical axis directed downward, so x = 0 is the top of the mountain and x = H is the bottom of the mountain; y as the horizontal axis beginning at the top of the mountain under study, where y = 0; and {x = x(s), y = y(s)} as the parametric equation of the curvilinear bed of the mountain on which the snow is lying, where s is the length of the curvilinear path along the bed and h(s) is the thickness of the snow layer (Fig. 3).

Fig. 3. Coordinate system.
We assume that the bed is rigid and the snow layer is thin so that |h(s) | ≪ H.
Suppose M(t) is the snowpack mass moving downhill under the gravity force along the curvilinear bed x = x(s), y = y(s). We assume that mass M has the shape of a parallelepiped with dimensions a × b × c, where c is the snow mass thickness normal to the bed surface, a is the frontal dimension normal to the direction of motion and b is the depth of the snow mass along its motion path.
Therefore, we have
where ρ is the density of the snow in moving mass M.
Due to the entrainment, when mass M(t) moves down, it absorbs ρ 0 h * ads amount of new snow over time dt, such that
where ρ 0 is the density of the intact snow on the mountain and s(t) is the length of the path of the avalanche. Some snow can also be deposited from the avalanche. The value of h * = h *(s) in Equation (21) therefore represents an effective difference between the snow influx and snow deposition, usually at the tail of the avalanche (Reference Bartelt, Buser and PlatzerBartelt and others, 2007). When the avalanche is well developed, the deposition equals the influx and h * = 0.
We assume that:
-
1. ρ 0 is constant or a known function of s, so that ρ 0 = ρ 0(s).
-
2. h(s) is constant or a known function of s.
Applying Newton’s law, the equation of motion for mass M, taking into account the entrainment, is
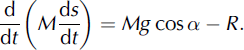
Here s(t) is the location of mass M on the bed; α is the angle between the xaxis and the direction of motion (Fig. 4) so that dx = (ds) cos α and dy = (ds) sin α; g = 9.81 m s−2; and R is the resistance force equal to the sum of the friction force plus the frontal resistance, R F, caused by the entrainment of the intact snow layer. For the friction force we use the Voellmy–Salm model (Reference VoellmyVoellmy, 1955; Reference Salm, Burkard and GublerSalm and others, 1990; Reference Bartelt, Salm and GruberBartelt and others, 1999), which decomposes R into dry Coulomb friction and ‘turbulent’ velocity-dependent resistance.

Fig. 4. An element of the motion path.
Therefore,

Here f is the Coulomb coefficient of dry friction on the snow–bed interface, ξ is the coefficient of ‘turbulent’ friction of the snow flow, k = dα/ds = 1/r is the curvature of the mountain bed and r is the radius of curvature. The term Mv 2 k describes the centrifugal force directed along the normal to the bed, which, depending on the curvature, either increases or decreases the normal force of interaction between the snow mass and the bed. The ‘turbulent’ friction term physically represents different velocity-dependent drag forces (e.g. air resistance at the front of the avalanche). According to Equation (6), frontal resistance R F is equal to
where K E is the entrainment toughness and h = h(s) is the incumbent snow thickness in the process zone.
The resistance force, R, substantially depends on the speed (ds/dt) of the moving mass, M (Fig. 5). The entrainment toughness, K E, and therefore the frontal resistance, R F, are greater as the snow is denser and older. We assume that K E is a constant depending on geographic and seasonal snow conditions. Also, we assume that a is a constant determined by the specific geometry of the track topography. Frontal resistance may be especially important during the initial stage of avalanche when the avalanche speed is small.

Fig. 5. Resistance force vs speed of moving mass.
6. Numerical Model: Governing Equations
Under these assumptions, from Equations (21–24) we get the closed equation system as follows:

and the initial conditions t = 0, s = 0, ds/dt = 0. Here cos α = dx/ds and sin α = dy/ds are some known functions of s found from the equation of the mountain bed, and k = dα/ds.
Integrating Equation (25) yields
where M 0 is the initial mass of the release zone. The mass of the avalanche, M, is therefore a function of s and can be determined from Equation (27) and M(s) is now a known function.
Let
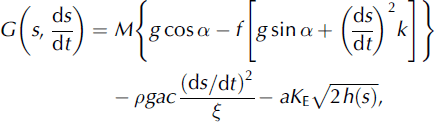
then we find, from Equation (25), the governing equation determining the motion of the snowpack mass, M, with time, t,
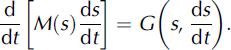
In a first series of simulations, we solve Equation (29) assuming that turbulent friction is neglected and curvature, k, is zero so G = G(s). In this case we have
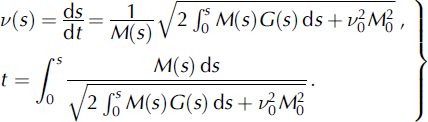
When curvature and/or turbulent friction are taken into account, G = G(s, ds/dt), Equation (29) can be transformed into the following form:
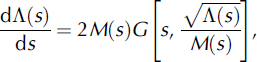
where Λ(s) = [M(s)v(s)]2, with initial conditions at s = 0, ds/dt = v = 0 and Λ = 0. Equation (31) can be integrated numerically, so that the speed of avalanche, v = v(s), can be found as a certain function of s, from which it follows that
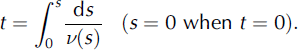
Equation (32) provides coordinate s of mass M as an implicit function of time, t. In the well-developed, steady-state regime, when h * = 0 and d2 s/dt 2 = 0, the speed of the avalanche is determined by equation R = Mg cos α, where R is a function of v 2 given in Equation (23).
7. Numerical Simulation
In this section we present a numerical simulation of the Vallée de la Sionne avalanche event of 7 February 2003 (Reference Sovilla, Burlando and BarteltSovilla and others, 2006). For this purpose, Equation (29) is solved taking into account both dry and turbulent friction, bed curvature and the frontal entrainment ignored by other models such as the Voellmy–Salm model.
The data for this event are reported by Reference Sovilla, Burlando and BarteltSovilla and others (2006). We summarize the data required for the numerical simulation as follows:
-
1. The release mass is 11.15 × 106 kg and the deposit mass is 17.16 × 106 kg.
-
2. Density is 200 kg m−3.
-
3. Coulomb friction is taken as f = 0.26 (Reference Platzer, Bartelt and KernPlatzer and others, 2007).
-
4. The slope angle and avalanche width are approximated as a function of the path length from the data given by Reference Sovilla, Burlando and BarteltSovilla and others (2006).
-
5. In accordance with the entrainment data of Reference Sovilla, Burlando and BarteltSovilla and others (2006), the entrainment depth, h *, that is the effective difference between snow influx and snow deposition, was assumed to be constant at the beginning of the avalanche up to 800 m of the path length, then to decrease linearly to zero between 800 and 1000 m of the path length, to remain zero between 1000 and 1600 m of the path length and, due to flank entrainment, to regain the original constant after 1600 m of the path length.
-
6. The ratio ρgac/ξ in the turbulent resistance term was assumed to remain constant. The value of ξ = 800 m s−2 was used here, taken from Reference Tiefenbacher and KernTiefenbacher and Kern (2004).
-
7. The frontal resistance, R F, was assumed to remain constant, R F = 0.1 MPa m.
-
8. The curvature of the mountain bed was determined from the slope angle curve given by Reference Sovilla, Burlando and BarteltSovilla and others (2006). This value was approximated and used over sections of the path length.
The result of the simulation using Equation (29) based on the above assumptions is shown in Figure 6. As seen, this simulation model is well confirmed by the experimental data reported by Reference Sovilla, Burlando and BarteltSovilla and others (2006).

Fig. 6. Velocity simulation of the Vallée de la Sionne avalanche event of 7 February 2003 using the data of Reference Sovilla, Burlando and BarteltSovilla and others (2006). Analytical results are compared with the observed data.
8. A Simple Estimate of Maximum Possible Acceleration of Avalanches
It is useful to get a simple estimate of avalanche acceleration. Let us assume that α = constant, so the mountain bed is represented by a straight-linear slope (Fig. 7), and let us ignore the frontal and ‘turbulent’ resistance. Also, we assume that M 0 = 0, v 0 = 0, that is, the initial mass and speed of the avalanche are zero. Further, we assume that ρ 0 ah * = F = constant. In this case, we find from Equations (25) and (26)
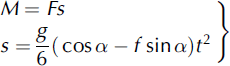
Thus, the acceleration, a A, of the avalanche cannot exceed
It will be a bit less if the frontal and ‘turbulent’ resistance forces are taken into account. For example, when α = 45°, we have from Equation (34)

Fig. 7. The simplest slope scheme.
9. Conclusions
Based on our entrainment model, the energy balance in the process zone was studied using the invariant Γ integral of fracture mechanics, and the frontal resistance and snow pressure were calculated. We introduced the entrainment toughness, K E, as a basic property characterizing the frontal resistance of the process zone and the frontal pressure in the avalanche. Some estimates of the entrainment toughness were derived from the physical properties of snow and from avalanche data of Reference Sovilla, Burlando and BarteltSovilla and others (2006). It was found that the specific dissipation energy of entrainment is commonly much less than the specific energy of avalanches, but for well-consolidated snow it can be comparable with the specific energy of any avalanche.
The entrainment model presented here can be implemented in simulation tools for two-dimensional models. The governing equations of the dynamics of avalanches were derived in the simplest approximation taking into account entrainment, inertia, gravitation and Voellmy–Salm friction; however, more work is required to understand the interaction between the flow rheology and entrainment.
Acknowledgement
The authors are greatly indebted to P. Bartelt for a very detailed, instructive and comprehensive commentary on the first version of this paper.











