1. Introduction
Strong ground motion can trigger snow avalanches. A large area around an earthquake epicenter may be subject to sufficient shaking (associated with S-waves) to produce failure of the snow cover. In the case of artificial seismicity induced by technogenic explosions, the effective range of such shaking is several kilometers (personal communication from N.V. Barashev, 2009), but it is up to a few hundred kilometers for strong earthquakes (e.g. Reference LaChapelleLaChapelle, 1968; Reference Higashiura, Nakamura, Nakamura and AbeHigashiura and others, 1979; Reference Singh, Ganju, Paul, Kumar and SharmaSingh and Ganju, 2002; Reference Podolskiy, Nishimura, Abe and ChernousPodolskiy and others, 2010). Avalanches due to either of these types of seismicity may claim human lives (Reference Singh, Ganju, Paul, Kumar and SharmaSingh and Ganju, 2002; personal communication from N.V. Barashev, 2009), block roads (Reference LaChapelleLaChapelle, 1968; Reference Higashiura, Nakamura, Nakamura and AbeHigashiura and others, 1979; Reference Ogura, Izumi, Miyazaki and KobayashiOgura and others, 2001) or perturb the mass balance of glaciers (Reference Tarr and MartinTarr and Martin, 1914). Reference Podolskiy, Nishimura, Abe and ChernousPodolskiy and others (2010) describe snow avalanches triggered by natural or artificial seismicity; importantly, they also note the lack of any comprehensive understanding of the mechanisms involved in triggering these events.
Previous attempts to understand the effects of seismicity on snowpack stability have included avalanche studies in the Khibiny mountains, Russia (Reference Chernous, Zuzin, Mokrov, Kalabin, Fedorenko and HusebyeChernous and others, 1999, Reference Chernous, Mokrov, Fedorenko, Husebye, Beketova and Stevens2002, Reference Chernous, Fedorenko, Mokrov, Barashev, Hewsby and Beketova2004, Reference Chernous, Fedorenko, Mokrov and Barashev2006; Reference MokrovMokrov, 2008), experimental work in Japan (Reference Abe and NakamuraAbe and Nakamura, 2005; Reference Nakamura, Abe, Hashimoto and OhtaNakamura and others, 2010) and theoretical work on the reduction in the stability index during shaking (Reference Ogura, Izumi, Miyazaki and KobayashiOgura and others, 2001; Reference Matsuzawa, Kajiya and ItoMatsuzawa and others, 2007). The importance of a high rate of shear loading has been demonstrated by Reference Abe and NakamuraAbe and Nakamura (2005), and further work is in progress (to be published elsewhere). However, the available information on the effects of seismicity on stressed snow is limited by a lack of detailed and precise measurements. Fundamental questions remain regarding the processes that underlie the fracturing of snow during shaking. Indeed, aside from two events described by Reference Higashiura, Nakamura, Nakamura and AbeHigashiura and others (1979) and Reference Ogura, Izumi, Miyazaki and KobayashiOgura and others (2001), earthquake-induced avalanches have not been documented in association with well-documented seismic records, details of the snow stratigraphy or the response of steep mountain slopes to strong ground motion (Reference Podolskiy, Nishimura, Abe and ChernousPodolskiy and others, 2010). Therefore, many of the theoretical assumptions in this field of study remain speculative, and more detailed experimental work must be undertaken to understand the nature of the response of snowpacks to strong ground motion.
We performed laboratory studies to quantify how vibrations (simulating strong ground motion) influence snow stability. The experiments were conducted in the Cryospheric Environmental Simulator (CES) at the Shinjo Branch of the Snow and Ice Research Centre at the National Research Institute for Earth Science and Disaster Prevention (NIED), Japan. We describe and discuss the shaking-table experiments, the methods and equipment used and the results obtained.
2. Methods
The method involved in our experiments requires the preparation of snow samples with potential weak layers and subjecting these to vibrations on a shaking table (Figs 1–3). The tests call for a variety of shaking modes. First, we considered the simplest case of shaking, which allowed only a single degree of freedom and oscillations in the horizontal direction. The shaking table was set at different inclinations. Second, we considered the more complex case of a double degree of freedom, with both horizontal and vertical components of acceleration, but with the shaking table always in the horizontal position. Our experiments with artificial snow were undertaken at a constant air temperature of −10°C and a constant relative humidity of 73%.

Fig. 1. Photographs of an artificial weak layer between two blocks of denser snow (block I): (a) vertical cross-section through the artificial ‘sandwich’ with a lamp behind it to show the weak layer; (b) aniline (C6H5NH2) 1 mm thick vertical cross-section of the weak layer; (c, d) microphotographs of the contact area between the bottom part of the weak layer (DFdc) and more dense snow (DFbk), which acted as the shear plane for most of the observed fracturing.

Fig. 2. The shaking table adjusted for horizontal oscillations and different inclinations (0°, 25° or 35°) and with a ‘sandwich’ type of snow block frozen to the metal platform and cut according to the inclination (35° in this photo). Small arrows indicate two accelerometers (installed horizontally). All blocks were dyed (vertical and normal bands) to aid in visualization of fracturing. Double-headed arrow indicates the direction of shaking.

Fig. 3. Pattern of the shaking-table clockwise oscillations for one full cycle before fracture (P4) and the principal points of trajectory P1–P4 (reference point is shown by dot on the ellipse, which represents the trajectory of the shaking platform, and arrows indicate the direction of movement). Frames of a video record show a snow sample before (P3) and after (P4) fracture.
2.1. Artificial ‘sandwiches’ of snow with a weak layer
Weak layers within a snowpack provide localized planes of shear that facilitate slab avalanche formation. For this reason we included a weak layer in our artificial snow samples for experiments on the shaking table. The snow we used was specially prepared at the CES snowfall facility. First, we grew artificial stellar dendrites (PPsd; the code numbers used here are taken from the classification proposed by Reference FierzFierz and others, 2009); on settling, these evolved into partly decomposed particles (DFdc), or, if the settling took place under a load, highly broken particles (DFbk). The weak layer was prepared by sifting a 5 cm layer of fresh snow (DFdc) through a close-meshed sieve over a block of compacted homogeneous snow (DFbk; 0.87 m × 0.87 m), putting another block of compacted homogeneous snow (DFbk) on top of the fresh snow, and leaving the samples to sinter for either 50 or 74 hours. This simple procedure allowed the weak layer of the ‘sandwich’ to settle and therefore strengthen the connection to the adjacent blocks (Fig. 1). Altogether, five large ‘sandwiches’ were prepared for vibration testing, with average densities of 222 kg m−3 in the lower blocks, 100 kg m−3 in the weak layers and 210 kg m−3 in the upper blocks (Table 1). The ‘sandwiches’ were then cut with a snow saw to form smaller blocks (length 0.29 m, width 0.20 m, height 0.17 m) which were frozen onto metal plates that had been warmed outside the cold laboratory to ∼23°C. This process firmly fixed the blocks to the shaking platform, ready for vibration testing. Samples used in tests on an inclined shaking platform (to simulate the natural shearing produced in snow subject to the force of gravity on a slope) were cut before mounting according to the selected slope angle (25° or 35°). All the blocks were characterized by two potential planes of shearing (the weak layer and the bottom surface of the block). This is reflected in the test results, where similar shear strengths of both these planes were observed (shown later). We could have concentrated fracturing in the weak layers by making the lower part of the ‘sandwich’ much denser and harder.
Table 1. Characteristics of artificial snow samples (all of which were ‘sandwiches’ with a weak layer) used for the shaking-table tests. All snow samples were prepared following exactly the same method, yet some unavoidable variations in parameters exist. For example, variations in the density of the weak layers may have arisen because it is difficult to measure density due to the small thickness of the horizon. For this reason, we provide mean values for an average sample

2.2. Shaking table and main adjustment modes
One of the basic tasks of earthquake engineering is to calculate the loading produced by the acceleration applied to the mass of a building during an earthquake; in other words, to calculate the inertial force. The inertial force must be known, for example, if one is to design a structure capable of standing up in an earthquake (Reference ReithermanReitherman,1997). We used the shaking table to observe the destabilization of snow, thereby enabling us to calculate the inertial forces involved.
The shaking table was specially constructed with horizontal and vertical oscillations driven by an electric motor (an increase in frequency increased the peak acceleration). The platform of the table could be adjusted for different modes of shaking (i.e. shaking with one degree of freedom, involving horizontal oscillations only, or shaking with two degrees of freedom, involving horizontal and vertical oscillations). The amplitude of shaking was 33 mm horizontally and 14 mm vertically. Different inclinations of shaking platform (0°, 25° and 35°) were considered for single degree-of-freedom mode (Fig. 2). The direction of shaking was always applied parallel to the longest side of the platform. During shaking with two degrees of freedom, the platform was always left in the horizontal position (Fig. 3). The oscillation frequency could be increased slowly or quickly to measure the effects of the rate of increase on peak accelerations (see section 3.2.5).
2.3. Principal measurements (accelerations and snow parameters)
Two horizontal components of acceleration (at the base and top of snow samples) and one vertical component (at the base, only in the case of tests with two degrees of freedom) were recorded continuously using ‘Kyowa’ AS-10/20HB acceleration transducers Fig. 3) at a sampling interval of 1 or 2 ms. When the shaking table was inclined at 25° or 35°, the acceleration transducer was always installed horizontally in the snow (following established practice in shaking-table tests related to landslide studies (e.g. Reference Asano, Matsuura, Okamoto and MatsuyamaAsano and others, 2003)). Before we analyzed the results, the acceleration records were calibrated and the fast Fourier transform (FFT) power spectra calculated (a rectangular time window was used). The acceleration records (denoted xs, base xb, base zb) display asymmetric amplitudes because of the inherent mechanical properties of the shaking table, but also in part because of the increased viscosity of the oil due to the low temperature of −10°C.
A high-speed camera (‘NAC C3’ HSV 500, synchronized with a stroboscope) was used to determine the movement pattern of the shaking table and the precise moment of snow fracturing. The recording frequency was 250 Hz.
For every test, we measured the mass, density, size of the snow block and area of shear plane failure, in order to calculate the shear strength of the snow and to determine the principal stresses at the moment of fracture. Toxic aniline was used to make 2-D cross-sections of the weak layer (Fig. 1b–d) in order to characterize and visualize the microstructure of the snow (Reference Kinosita and WakahamaKinosita and Wakahama, 1960).
3. Results and Discussion
3.1. Video record of fractures
We could detect the occurrence of fractures with the aid of video records (e.g. Figs 3 and 4) by comparing these with the records of acceleration and by noting the abrupt disagreement between acceleration signals in the snow and on the shaking platform. With the help of this information, we were able to determine the peak accelerations responsible for fracturing, as discussed in more detail below.

Fig. 4. Sequence of high-speed video frames (a–e) showing (b) the moment of snow sample fracture under single degree-of-freedom horizontal oscillations (sample 20; Table 3). Long arrows indicate the moments corresponding to the accelerogram (f). The circle in (f) indicates fracture nucleation (b).
The two principal types of fracturing (Table 2) are single fractures, which develop either along the bottom of the snow block (also reported by Reference Abe and NakamuraAbe and Nakamura, 2005; Reference Nakamura, Abe, Hashimoto and OhtaNakamura and others, 2010) or along the weak layer; and double fractures, which develop in two stages, first along the shear plane at the bottom of the lower specimen (primary fracturing) and then during the next phase of shaking, along the weak layer (secondary fracturing). For the complete set of our experiments, 40% of fractures occurred along the bottom and 60% along the weak layer; only a few double fractures were observed. Fracturing at the base of natural packs of snow and within natural weak layers is known to occur during real earthquake-induced avalanching. For example, avalanche failure along the base was documented by Reference Ogura, Izumi, Miyazaki and KobayashiOgura and others (2001), failure along weak layers was described by Reference Higashiura, Nakamura, Nakamura and AbeHigashiura and others (1979) and both types were described by Reference LaChapelleLaChapelle (1968).
Table 2. Summary of observed types of fractures and total number of similar fractures. These are classified according to the type of oscillation, inclination, location of fracturing (within the bottom or weak layers) and the ‘background’ normal stress at the moment of fracture. A dash indicates a type of fracturing that is impossible for the particular mode of oscillation. d.f., degree of freedom

We define tension as negative normal pressure, and compression as positive. In the present tests with an inclined shaking table, all primary and most secondary fracturing occurred under negative normal pressures (see section 3.2.1) and only two secondary fractures (along weak layers) developed during compression. As a consequence of primary fracturing, the platform and the block of fractured snow started moving relative to each other. This corresponded to a reduction in friction during the initial stage of downslope movement of the block of fractured snow. Double fractures developed before snow started to move.
Video records of double degree-of-freedom oscillations demonstrate that the vibrations of the shaking table display a clockwise elliptical trajectory. The snow block acts as a rudimentary and rather stiff oscillator; it simply moves with the shaking table. The single particle trajectory of the shaking platform and its speed as tracked by video analysis correspond well with measured accelerations, showing the same asymmetry (see section 2.3) at higher frequency for the segment P3–P4–P1 and at lower speeds for P1–P2–P3 (Fig. 3). Owing to this movement, all fractures occur at the same trajectory point, P4, where the shear and tensile forces applied to the snow sample reach a maximum value (Fig. 3) (see sections 3.2.3 and 3.2.4).
3.2. Oscillations and fracturing of the snow sample
3.2.1. Shear stress caused by shaking
When the shaking table moves the base of a frozen snow sample, its mass experiences inertia, since the snow attempts to follow the motion of the shaking table. Therefore, the maximum of an applied force corresponds to the peak acceleration, a p (as deduced from high-speed video records and accelerograms (e.g. Fig. 4)) at the instant when the shaking platform reverses direction. Horizontal accelerations of a shaking table give rise to shear stresses within the snow sample and since the acceleration reverses due to the trajectory of the shaking platform, the direction of shear stresses also reverses (always for horizontal tests and almost always for inclined tests). By dividing applied inertial force by the area of the plane of shearing (Reference Abe and NakamuraAbe and Nakamura, 2005; Reference Nakamura, Abe, Hashimoto and OhtaNakamura and others, 2010) (Fig. 5), the critical shear strength of the snow can be calculated:
where τ is the shear strength, m f is the mass of fractured snow, a p is the peak acceleration causing fractures (e.g. Fig. 6), g is the gravitational acceleration and A is the area of the shear plane. These values were determined from our test records or measured directly during testing.

Fig. 5. Conceptual model for calculating the shear stress (and shear strength) during the application of inertia to a snow block causing fracturing (a) along the weak layer and (b) along the bottom. F is the force applied to snow by inertia, a p is the horizontal peak acceleration, m f is the mass of fractured snow, m l is the mass of snow left after fracturing and A the area of the shear fracture surface.

Fig. 6. Example of acceleration records and FFT power spectra for an experiment on the shaking table (sample 1). The instant of fracturing is shown by an arrow and a circle. Arrows indicate the dominant ranges of vibration frequency. Double-headed arrows indicate directions of measured accelerations.
For tests with an inclined shaking table, the natural shearing, τ n, due to a mass of snow over the shear plane should be included (Fig. 7a) and it is given by

The resulting net force and its direction are determined by the sum of force vectors produced by acceleration τ ap and the weight of snow in the gravitational field (Fig. 7b). This vector sum applied to a mass of snow can be broken down into two components, shearing, τ st, and the normal to the shear plane, where
Most of the shear strength values (within 2σ) calculated in the present study fall in the range 1.0–2.4 kPa (Table 3). The values are high compared with values for dry coherent snow presented by Reference MellorMellor (1975), demonstrating that microstructure is more important in influencing strength than is density (e.g. Reference Voitkovsky, Bozhinsky, Golubev, Laptev, Zhigulsky and SlesarenkoVoitkovskiy and others, 1975; Reference Schweizer, Jamieson and SchneebeliSchweizer and others, 2003).

Fig. 7. (a) Stresses in a snowpack due to weight without shaking. (b, c) Principal stress tensor components at the moment of fracture: (b) fracturing typical in most of the tests at the left side of the trajectory with negative normal pressure and (c) possible fracturing at the right side with increased normal pressure. m f is the mass of the fractured snow block, σ n is the normal shearing caused by the mass of snow along the shear plane, τ ap is the force produced by acceleration, τ st and τ sc are the shear components of the net force, σ t is the tensile component of the net force, σ c is the compressive component of the net force, A is the area of the shear plane, α is the slope inclination (angles and lengths of vectors are not absolute values; the dot on the curved arrow indicates the point of oscillation).
Table 3. Principal measured and calculated parameters for vibration-induced fractures

The orientation of the slope of the shaking table determined the principal direction of the net force, and most of the fractures occurred at the furthest left-hand point of the shaking-table trajectory (Fig. 2). At this point we always had stress conditions, which not only shear the snow but also pull the block away from the slope, i.e. a negative normal pressure or tension, σ t (Fig. 7b), where σ t is expressed as
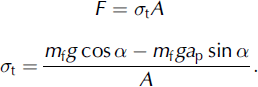
During the opposite phase of oscillation (at the furthest right-hand point of the shaking-table trajectory), the block of snow is pushed into the slope (i.e. an increase in normal pressure or compression, σ c; Fig. 7c), where
and
Only two secondary fractures, in samples 32 and 33 (Table 3), were observed from video records to form at this phase of oscillation. (If compared with the static condition, the normal pressure was three times higher at the moment of fracture, though it was smaller than the compressive strength of snow and was not a direct cause.)
3.2.2. Measured accelerations
An FFT power spectrum analysis of the obtained accelerograms shows a significant number of maxima falling within the frequency range 2–3 Hz. This can be related to the number of oscillations performed by the shaking table (Fig. 6). Even though the prevailing maximum values for the response spectra of the shaking table (e.g. 2.7 Hz) are higher than the absolute values of ground response typical for earthquakes (e.g. Reference KramerKramer, 1996), the range of loading times (the time interval ∼50 ms during which inertia was applied consequential to a reversal of the movement vector of the shaking table) still yields brittle fracture in snow (e.g. Reference Föhn and CamponovoFöhn and Camponovo, 1997).
The measured peak horizontal accelerations responsible for fractures vary from 1.92 to 7.03 g (Fig. 8). The peak vertical accelerations at the moment of fracturing range from 0.41 to 2.37 g (Table 3). Given that the extremes for natural peak ground accelerations observed anywhere in the world are between 1.0 g and 3.0 g for horizontal accelerations (Reference Anderson, Lee, Kanamori, Jennings and KisslingerAnderson, 2003) and 3.8 g for vertical accelerations (Reference Aoi, Kanugi and FujiwaraAoi and others, 2008), the accelerations in our experiments are rare or too high for natural seismicity. However, it was necessary to subject our small and low-mass snow samples to such high accelerations (Table 3) because the induced shear force is proportional to the mass of the snow sample (Equation (1)). This explains why heavier samples fracture at lower values of peak acceleration and why there is no relationship between shear strength and peak acceleration (Fig. 8). If larger masses of snow were used over the shear plane, much smaller values of acceleration, closer to natural tremors, would suffice for fracturing (see section 3.3).

Fig. 8. Peak horizontal accelerations compared with the corresponding shear strengths.
3.2.3. Normal stress oscillations under double degreeof-freedom shaking
The stress state of the snow block under double degree-offreedom oscillations can be discussed in terms of both normal and shear stresses and it is of interest to estimate the contributions of these stresses to the stress tensor. If we adopt the common geological convention of treating compressive stress as positive normal pressure and tensile stress as negative, it is possible to represent them both on one axis of normal stress (acting in the shear plane). Oscillation of normal stress is a function of the vertical component of acceleration. Considering only the normal stress variations between principal points of the shaking-table trajectory (P1–P4; Fig. 3), we can see two points with normal stress under normal gravity (P1 and P3, around 0.3 kPa), one point with compressive stress due to an upward movement and increasing weight (P2, around 0.7 kPa; insufficient to reach the compressive strength (Reference MellorMellor, 1975)) and one point with tensile stress normal to the shear plane due to a downward movement with significant negative vertical acceleration (P4, around 0.45 kPa). If we show on one diagram (Fig. 9) the shear and normal stress oscillations for one full oscillation before fracture, we find that the fracturing of blocks of snow always occurs at the particular shear stress and shear strength reached at a point in the shaking-table trajectory (P4) that induced a negative normal stress (tensile stress) (Table 3).

Fig. 9. Example of oscillations of shear and normal stress as a function of horizontal and vertical components of acceleration between the principal points on the trajectory (P1–P4) for one full cycle of the platform’s oscillation before fracture (for a double degree-of-freedom test, sample 1). Principal points of the trajectory are shown on the ellipse. The arrow marks the direction of the platform’s movement. P4 corresponds to the point of fracture (see Fig. 3 for more details).
3.2.4. Significance of normal stress oscillations
When adopting the same convention as described above to represent stresses for all tests, we can see differences between tests with and without normal stress oscillations (Fig. 10). If we compare the shear strength values with the normal stress for different tests and types of fracturing, we see that almost all fractures for inclined or double degree-offreedom tests formed when the normal pressure was negative (Fig. 10b–d and f–h). The absolute values of these tensile stresses were smaller than the values of the shear strength of snow and, if we assume that the tensile strength of low-density snow is higher than the shear strength (Reference MellorMellor, 1975), they would seem to be insufficient to reach the tensile strength of the snow samples. Reference MellorMellor (1975) and Reference NaritaNarita (1980) have discussed the effects of tensile stresses in uniform snow, but we are not aware of any experiments investigating the tensile strength of weak snow layers. Our experiments indicate that higher vibration-induced tensile stress (∼1 kPa) can be sufficient to fracture snow, even without shearing. Moreover, we should note that, in accordance with the empirical function for tensile strength as a function of snow density (Reference Jamieson and JohnstonJamieson and Johnston, 1990), our stresses are close to the tensile strength of low-density snow (0.4 kPa and 100 kg m−3 respectively).

Fig. 10. Normal stress as a function of shear strength for different types of test (a positive normal stress represents compression; a negative stress represents tension). (a) Single degree-of-freedom bottom fracture, inclination 0°; (b) single degree-of-freedom bottom fracture, inclination 25°; (c) single degree-of-freedom bottom fracture, inclination 35°; (d) double degree-of-freedom bottom fracture, inclination 0°; (e) single degree-of-freedom weak-layer fracture, inclination 0°; (f) single degree-of-freedom weak-layer fracture, inclination 25°; (g) single degree-of-freedom weak-layer fracture, inclination 35°; (h) double degree-of-freedom weak-layer fracture, inclination 0°.
When comparing all fractures along the weak layer and the bottom, differences in the shear strength are apparent for weak-layer fractures (Fig. 11). Fractures along the weak layer that formed under tension are weaker than fractures formed under compression (Fig. 11a). In contrast, failures at the bottom of the snowpack do not show this relationship (Fig. 11b). The principal structural characteristics of the snow in the vicinity of the shear planes could determine such differences in performance. Bottom fractures occurred within a uniform stratum of the snow block or at the boundary with the metal plate, whereas weak-layer fractures were always propagated in snow through a potential failure plane with stress concentration. The concentration of tensile stress around a crack tip should favour crack propagation in an inherently weaker plane than in stressed uniform material.

Fig. 11. Calculated shear strengths for (a) the weak layer and (b) the bottom compared with the normal stress at the moment of fracture for all tests (a positive normal stress represents compression; a negative stress represents tension).
We suggest that stratified snow is stronger in tests without tension and weaker in tests with a tensile component of stress. Indeed, for a brittle material such as snow, a high-rate tensional stress normal to the shear plane may be important and contribute to the nucleation of shear failure. Furthermore, this condition is almost unique to snow, being uncommon in rocks and other porous materials because their tensile strength is an order of magnitude larger than for snow (MPa compared with kPa) and because the earthquake-induced tensile stress reaches a critical level of snow strength. For example, because of the high strength of other engineering materials (e.g. rocks) and as a result of the significant underestimation of possible maximum values of the vertical component of acceleration, vertical accelerations were ignored until the 1960s and were not included in building codes (Reference Newmark and RosenbluethNewmark and Rosenblueth, 1971). Of relevance here is the recent extreme of 3.8 g vertical acceleration during the Iwate–Miyagi earthquake, as reported by Reference Aoi, Kanugi and FujiwaraAoi and others (2008).
3.2.5. Shear strength and the duration of vibrating
One interesting observation was made with regard to the shear strength of snow and the duration of vibrating. If we consider the double degree-of-freedom tests, with fracturing along the weak layer, normal stress oscillations and a lengthy period of vibrations, we obtained a correlation coefficient of 0.84 (for seven samples) between the shear strength and duration of vibrating, indicating a possible linear relationship (Table 3).
The calculated shear strength becomes smaller with smaller periods of vibration (from 21.5 to 2.2 s), possibly related to the well-established effects of densification of soils, when for example sands, soils or clays consolidate, compact and settle when subjected to intense vibrations. Based on this assumption and the fact that snow crystals in the weak layers are full of voids between dendrites (Fig. 1), we suggest that ground vibrations (if insufficient for fracturing) can increase the stability and strength of low-density snow layers (as suggested by Reference Podolskiy, Nishimura, Abe and ChernousPodolskiy and others, 2010) by settling and increasing the density, thereby increasing the size and number of snow-grain bonds per unit volume. Therefore, two processes, controlled by the magnitude of earthquake and shaking duration, affect the properties of the snow, although they require further clarification and study. These processes probably help to stabilize a slope after seismicity that has not triggered an avalanche.
3.3. Simplified applications of the experimental data
It is interesting to apply the results of our experiments to a snowpack on an inclined slope subjected to realistic acceleration and using the simple inverse method (i.e. determine critical amount of snow, m f, through known shear strength, τ, and some assumed peak acceleration, a p; Equation (1)). If we assume typical values for horizontal accelerations during a strong earthquake (acting perpendicular to the slope), a surface slope angle of 38° (typical for most dry-slab avalanches; Reference PerlaPerla, 1977) and snow with the same densities as those we measured in fractured blocks as well as the corresponding shear strength values for the snow, we can estimate a critical thickness for the snow covering the weak layer by
where m f can be extracted from Equation (3). This gives

and Equation (7) now becomes
where ρ is the density of the snow covering the weak layer, a p is the peak horizontal acceleration (here we assume 0.5 g as the most commonly mapped value for strong earthquake hazard assessment (e.g. Reference Giardini, Gruenthal, Shedlock, Zhang, Lee, Kanamori, Jennings and KisslingerGiardini and others, 2003)), and α is the slope angle (assume 38°) (Table 3). For example, a peak horizontal acceleration of 0.5 g will create a critical situation for a weak layer with a shear strength of 1.2 kPa (average) given 0.58 m of snow cover (Fig. 12). Figure 13 shows the relationship between a wider range of horizontal accelerations (0–1 g) and slope inclinations (17–60°) for the same snow in each case. These examples demonstrate that typical realistic values (of acceleration and shear strength) can lead to unstable situations.

Fig. 12. Snow thickness as a function of horizontal peak ground acceleration (for shear strength 1200 Pa, shear plane inclined at 38°, density 210 kg m−3). Curve shows the snow thickness required for failure, i.e. critical thickness values for fracture, over the range of horizontal peak accelerations.

Fig. 13. Critical value of snow thickness (density 210 kg m−3) for various accelerations (0–1 g) and slope inclinations (17°, 38° and 60°) over a weak layer with a shear strength of 1200 Pa.
The same simplified approach can be used to estimate the accelerations that affected the slope at the moment of snow fracturing during the 1964 Great Alaskan Earthquake (at that time there were no seismic instruments capable of recording strong ground motion; Reference KrauskopfKrauskopf, 1968). It is possible that the calculations could be based on an analysis of the photographs published by Reference LaChapelleLaChapelle (1968), although there are too many unknown parameters to enable precise results to be attained.
4. Summary
We have described experiments with snow on a shaking table in an attempt to understand the mechanisms involved in earthquake-induced avalanches. We employed various new approaches such as using specially prepared artificial snowpack ‘sandwiches’ that contained a weak layer and calculating the stresses produced by inertia for single degree-of-freedom vibrations with the shaking platform set at various angles, and for double degree-of-freedom oscillations. Our experimental results help confirm, demonstrate and support the following conclusions:
-
1. Shaking during strong ground motion can produce fracturing within a homogeneous or stratified snow block as a result of the inertial forces induced by acceleration.
-
2. In common with our shaking-table experiments, the stress tensor produced during the loading of snow, consequential to an earthquake, has shear, tensile and compressive components.
-
3. It is usually the case that avalanches associated with natural triggers or human activity occur with a positive normal stress (compression). In contrast, a high-rate tensional force oriented normal to the shear plane is possible only during earthquakes, not during other natural processes. This tension can be an important factor in the nucleation of certain fractures in the snow which are almost unique because brittle snow is one of the weakest materials under tension known in geology. Although such fracturing is uncommon in other materials, cohesive sand and piles of ash probably behave similarly.
-
4. The shear strength of a weak layer is smaller under tensile stress (more pure tensile tests and compression-shear tests are needed for construction of a dynamic Mohr-Coulomb failure envelope).
-
5. It is likely that prolonged vibrations (responsible for normal stress oscillations but insufficient for failure) can increase the shear strength of snow.
-
6. Shaking may contribute significantly to the initial stages of snow slab disintegration and accordingly may influence the avalanche flow parameters (it is likely that the coefficient of kinetic friction is affected, as rapid shattering of the original slab will provide smaller particles at the initial stages of motion).
Further work is needed for a better understanding of how strong ground motion influences the stability of snowpacks on a larger scale. We then need to investigate how to incorporate knowledge into avalanche forecasting. Ideally, the Kyoshin net (K-NET), which transmits strong-motion data on the Internet in real time, coupled with a snowpack model (e.g. SNOWPACK; Reference Bartelt and LehningBartelt and Lehning, 2002) could provide useful information about the probability of collapse on a snow-covered slope before the arrival of S-waves. However, in the meantime, predictions of earthquake-induced avalanches remain a problem for the future.
Acknowledgements
We thank P. Bartelt and T.H. Jacka for editorial assistance. The initial version of this paper benefited enormously from extensive reviews by T. Faug and an anonymous reviewer. We thank S. Mochizuki and G. Okawa for support during experiments. We acknowledge technical support and provision of equipment from K. Shinbori, who engineered the shaking table, and from K. Kosugi, who assisted with highspeed video processing. These experiments would not have been possible without permission from T. Sato to use the CES facility. This work was supported by Grants-in-Aid for Scientific Research (18651093), by a grant of the Russian Foundation for Basic Research (05-05-64368-A), and by a scholarship for foreign students provided by the Ministry of Education, Culture, Sports, Science and Technology, Japan. We also thank D.A. Short and A. Stallard for improvements to our written English.




















