Article contents
Wake structure of laminar flow past a sphere under the influence of a transverse magnetic field
Published online by Cambridge University Press: 20 June 2019
Abstract
The wake structure of an incompressible, conducting, viscous fluid past an electrically insulating sphere affected by a transverse magnetic field is investigated numerically over flow regimes including steady and unsteady laminar flows at Reynolds numbers up to 300. For a steady axisymmetric flow affected by a transverse magnetic field, the wake structure is deemed to be a double plane symmetric state. For a periodic flow, unsteady vortex shedding is first suppressed and transitions to a steady plane symmetric state and then to a double plane symmetric pattern. Wake structures in the range 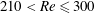 $210<Re\leqslant 300$ without a magnetic field have a symmetry plane. An angle
$210<Re\leqslant 300$ without a magnetic field have a symmetry plane. An angle 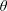 $\unicode[STIX]{x1D703}$ exists between the orientation of this symmetry plane and the imposed transverse magnetic field. For a given transverse magnetic field, the final wake structure is found to be independent of the initial flow configuration with a different angle
$\unicode[STIX]{x1D703}$ exists between the orientation of this symmetry plane and the imposed transverse magnetic field. For a given transverse magnetic field, the final wake structure is found to be independent of the initial flow configuration with a different angle 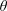 $\unicode[STIX]{x1D703}$. However, the orientation of the symmetry plane tends to be perpendicular to the magnetic field, which implies that the transverse magnetic field can control the orientation of the wake structure of a free-moving sphere and change the direction of its horizontal motion by a field–wake–trajectory control mechanism. An interesting ‘reversion phenomenon’ is found, where the wake structure of the sphere at a higher Reynolds number and a certain magnetic interaction parameter (
$\unicode[STIX]{x1D703}$. However, the orientation of the symmetry plane tends to be perpendicular to the magnetic field, which implies that the transverse magnetic field can control the orientation of the wake structure of a free-moving sphere and change the direction of its horizontal motion by a field–wake–trajectory control mechanism. An interesting ‘reversion phenomenon’ is found, where the wake structure of the sphere at a higher Reynolds number and a certain magnetic interaction parameter (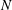 $N$) corresponds to a lower Reynolds number with a lower
$N$) corresponds to a lower Reynolds number with a lower 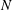 $N$ value. Furthermore, the drag coefficient is proportional to
$N$ value. Furthermore, the drag coefficient is proportional to 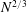 $N^{2/3}$ for weak magnetic fields or to
$N^{2/3}$ for weak magnetic fields or to 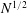 $N^{1/2}$ for strong magnetic fields, where the threshold value between these two regimes is approximately
$N^{1/2}$ for strong magnetic fields, where the threshold value between these two regimes is approximately 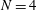 $N=4$.
$N=4$.
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 8
- Cited by





