Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Xia, Yi
Lin, Jianzhong
Ku, Xiaoke
and
Chan, Tatleung
2018.
Shear-induced autorotation of freely rotatable cylinder in a channel flow at moderate Reynolds number.
Physics of Fluids,
Vol. 30,
Issue. 4,
Ryu, Sungmin
2018.
Quadrant analysis on vortex-induced autorotation of a rigid square cylinder.
Journal of Mechanical Science and Technology,
Vol. 32,
Issue. 6,
p.
2629.
Pan, Zhenhai
Chen, Zhuo
and
Wu, Huiying
2019.
Self-excited rotation and flow dynamics across a freely rotatable square cylinder confined between two parallel walls.
Physics of Fluids,
Vol. 31,
Issue. 8,
Shao, J.Y.
Shu, C.
Liu, N.Y.
and
Zhao, X.
2019.
Numerical investigation of vortex induced rotation of two square cylinders in tandem arrangement.
Ocean Engineering,
Vol. 171,
Issue. ,
p.
485.
Wang, Hua-kun
Yan, Yu-hao
Chen, Can-ming
Ji, Chun-ning
and
Zhai, Qiu
2019.
Numerical Investigation on Vortex-Induced Rotations of A Triangular Cylinder Using An Immersed Boundary Method.
China Ocean Engineering,
Vol. 33,
Issue. 6,
p.
723.
Wang, Huakun
Zhai, Qiu
and
Chen, Kaixiao
2019.
Vortex-induced vibrations of an elliptic cylinder with both transverse and rotational degrees of freedom.
Journal of Fluids and Structures,
Vol. 84,
Issue. ,
p.
36.
Xiong, Yongliang
Peng, Sai
Zhang, Mengqi
and
Yang, Dan
2019.
Numerical study on the vortex-induced vibration of a circular cylinder in viscoelastic fluids.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 272,
Issue. ,
p.
104170.
Herreros, M. I.
and
Ligüérzana, S.
2020.
Rigid body motion in viscous flows using the finite element method.
Physics of Fluids,
Vol. 32,
Issue. 12,
p.
123311.
Hu, Ruifeng
and
Tang, Hui
2020.
An elliptic foil rotating in uniform low-Reynolds-number flows.
Fluid Dynamics Research,
Vol. 52,
Issue. 5,
p.
055509.
Li, Lichun
Yan, Zhe
and
Pan, Zhenhai
2021.
Vortex-induced rotations of two side-by-side square cylinders in a two-dimensional microchannel.
Physics of Fluids,
Vol. 33,
Issue. 11,
Wang, Shubiao
Cheng, Wenming
Du, Run
Wang, Yupu
and
Chen, Qingrong
2021.
Flow-induced vibration of a trapezoidal cylinder at low Reynolds numbers.
Physics of Fluids,
Vol. 33,
Issue. 5,
Shahzer, Md.Abu
Khan, Mohd.Athar
and
Anwar, Syed Fahad
2021.
Fluid Mechanics and Fluid Power.
p.
597.
Hosseinjani, Ali Akbar
and
Akbari, Ghasem
2022.
Numerical study of vortex-induced autorotation of an elliptic blade in lid-driven cavity flow.
Fluid Dynamics Research,
Vol. 54,
Issue. 6,
p.
065503.
Tang, Tao
Zhu, Hongjun
Song, Jinze
Ma, Bowen
and
Zhou, Tongming
2022.
The state-of-the-art review on the wake alteration of a rotating cylinder and the associated interaction with flow-induced vibration.
Ocean Engineering,
Vol. 254,
Issue. ,
p.
111340.
Li, Lichun
Liu, Jiazheng
and
Pan, Zhenhai
2022.
Enhancement of heat transfer and mixing with two side-by-side freely rotatable cylinders in microchannel.
International Journal of Heat and Mass Transfer,
Vol. 189,
Issue. ,
p.
122717.
Shahzer, Mohammad Abu
Khan, Mohammad Athar
Anwer, Syed Fahad
Khan, Saleem Anwar
Khan, Mohammad Shoaib
Algethami, Abdullah
and
Alsehli, Mishal
2022.
A comprehensive investigation of vortex-induced vibrations and flow-induced rotation of an elliptic cylinder.
Physics of Fluids,
Vol. 34,
Issue. 3,
Xie, Zhihua
Lin, Pengzhi
and
Stoesser, Thorsten
2022.
A conservative and consistent implicit Cartesian cut-cell method for moving geometries with reduced spurious pressure oscillations.
Journal of Computational Physics,
Vol. 459,
Issue. ,
p.
111124.
Alam, Md. Mahbub
2023.
Flow-induced rotation and wake characteristics of polygonal prisms subjected to laminar flow.
Physics of Fluids,
Vol. 35,
Issue. 5,
Luo, Chensheng
Mou, Ruiyong
Huang, Xingrong
Huang, Wei-Xi
and
Fang, Le
2023.
A free-streamline boundary-layer model for small-amplitude oscillation regime of square cylinder under vortex-induced rotation.
Physics of Fluids,
Vol. 35,
Issue. 9,
Rath, Subhasisa
Mittal, Charu
Abhishek
and
Sharma, Atul
2024.
Channel-confined flow-induced rotation of an asymmetrically confined square cylinder in a two-dimensional laminar flow regime.
Physics of Fluids,
Vol. 36,
Issue. 2,
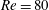 $Re=80$ and (ii) their step increases in the autorotation regime.
$Re=80$ and (ii) their step increases in the autorotation regime.




