Hostname: page-component-76fb5796d-x4r87 Total loading time: 0 Render date: 2024-04-26T05:04:09.429Z Has data issue: false hasContentIssue false
  • English
  • Français

Viscous effects in Mach reflection of shock waves and passage to the inviscid limit

Published online by Cambridge University Press:  15 March 2023

G.V. Shoev Open the ORCID record for G.V. Shoev [Opens in a new window] ,
A.N. Kudryavtsev Open the ORCID record for A.N. Kudryavtsev [Opens in a new window] ,
D.V. Khotyanovsky Open the ORCID record for D.V. Khotyanovsky [Opens in a new window]  and
Ye.A. Bondar Open the ORCID record for Ye.A. Bondar [Opens in a new window]
G.V. Shoev*
Affiliation:
Khristianovich Institute of Theoretical and Applied Mechanics, 630090 Novosibirsk, Russia
A.N. Kudryavtsev
Affiliation:
Khristianovich Institute of Theoretical and Applied Mechanics, 630090 Novosibirsk, Russia
D.V. Khotyanovsky
Affiliation:
Khristianovich Institute of Theoretical and Applied Mechanics, 630090 Novosibirsk, Russia
Ye.A. Bondar
Affiliation:
Khristianovich Institute of Theoretical and Applied Mechanics, 630090 Novosibirsk, Russia
*
†Email address for correspondence: shoev@itam.nsc.ru
Get access Rights & Permissions [Opens in a new window]

Abstract

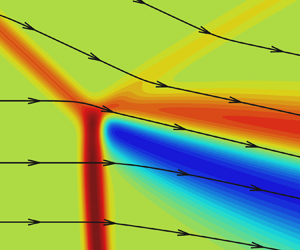
The influence of viscosity on the Mach reflection of shock waves in a steady flow of a monatomic gas is studied by solving the Navier–Stokes equations numerically. Based on the nested block grid refinement technique, the flow near the shock wave intersection is simulated, and its behaviour with increasing Reynolds number is studied. The computations are performed for the interaction of both strong (free-stream Mach number $M_\infty = 4$) and weak ($M_\infty = 1.7$) shock waves. In the strong reflection of shock waves at all Reynolds numbers in the examined range, it is found that there exists a small-size zone behind the shock wave intersection where the flow parameters differ from those predicted by the Rankine–Hugoniot relations and hence deviate from the predictions of the inviscid three-shock theory. The structure of this zone is self-similar: in coordinates normalised to the mean free path of molecules in the free stream. The structure is identical at all Reynolds numbers considered in the study. As the Reynolds number increases, the size of this zone in physical coordinates decreases, but the maximum difference between the viscous and inviscid solutions in this zone remains constant, reaching approximately $10\,\%$ for pressure. In the weak reflection of shock waves, the flow structure behind the shock wave intersection is not self-similar, i.e. the flow fields at different Reynolds numbers do not coincide in the normalised coordinates, but converge, as the Reynolds number increases, to the parameters predicted by the inviscid three-shock theory.

JFM classification

Compressible Flows: Shock waves Compressible Flows: Gas dynamics Compressible Flows: Supersonic flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 959 , 25 March 2023 , A2
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adrianov, A.L., Starykh, A.L. & Uskov, V.N. 1995 Interference of Stationary Gas Dynamic Discontinuities. Nauka.Google Scholar
Ben-Dor, G. 2007 Shock Wave Reflection Phenomena. Springer.Google Scholar
Ben-Dor, G., Takayama, K. & Needham, C.E. 1987 The thermal nature of the triple point of a Mach reflection. Phys. Fluids 30 (5), 1287–1293.CrossRefGoogle Scholar
Bird, G. 1994 Molecular Gas Dynamics and the Direct Simulation of Gas Flows. Clarendon.Google Scholar
Chen, H., Zhang, B. & Liu, H. 2016 Non-Rankine–Hugoniot shock zone of Mach reflection in hypersonic rarefied flows. J. Spacecr. Rockets 53 (4), 1–10.CrossRefGoogle Scholar
Defina, A., Susin, F. & Viero, D. 2008 a Numerical study of the Guderley and Vasilev reflections in steady two-dimensional shallow water flow. Phys. Fluids 20 (9), 097102.CrossRefGoogle Scholar
Defina, A., Viero, D. & Susin, F. 2008 b Numerical simulation of the Vasilev reflection. Shock Waves 18 (3), 235–242.CrossRefGoogle Scholar
Emanuel, G. 2013 Shock Waves Dynamics: Derivatives and Related Topics. CRC.Google Scholar
Gilbarg, D. & Paolucci, D. 1953 The structure of shock waves in the continuum theory of fluids. J. Rat. Mech. Anal. 2, 617–642.Google Scholar
Guderley, K. 1947 Considerations on the structure of mixed subsonic supersonic flow patterns. Tech. Rep. F-TR-2168-ND. AAF, Air Material Command (Wright Field).Google Scholar
Guderley, K. 1962 The Theory of Transonic Flow. Pergamon.Google Scholar
Hamel, G. 1916 Spiralfömrige bewegungen zäher flüssigheiten. Jber. Dtsch. Math-Ver. 25, 34–60.Google Scholar
Hornung, H. & Robinson, M. 1982 Transition from regular to Mach reflection of shock wave. Part 2. The steady-flow criterion. J. Fluid Mech. 123, 155–164.CrossRefGoogle Scholar
Hunter, J. & Brio, M. 2000 Weak shock reflection. J. Fluid Mech. 410, 235–261.CrossRefGoogle Scholar
Hunter, J.K. & Tesdall, A.M. 2004 Weak shock reflection. In A Celebration of Mathematical Modeling: The Joseph B. Keller Anniversary Volume (ed. D. Givoli, M.J. Grote & G.C. Papanicolaou), pp. 93–112. Springer.CrossRefGoogle Scholar
Ivanov, M., Bondar, Ye., Khotyanovsky, D., Kudryavtsev, A. & Shoev, G. 2010 a Viscosity effects on weak irregular reflection of shock waves in steady flow. Prog. Aerosp. Sci. 46 (2), 89–105.CrossRefGoogle Scholar
Ivanov, M., Bonfiglioli, A., Paciorri, R. & Sabetta, F. 2010 b Computation of weak steady shock reflections by means of an unstructured shock-fitting solver. Shock Waves 20 (4), 271–284.CrossRefGoogle Scholar
Ivanov, M., Markelov, G. & Gimelshein, S. 1998 Statistical simulation of reactive rarefied flows – numerical approach and applications. In 7th AIAA/ASME Joint Thermophysics and Heat Transfer Conference, Albuquerque, NM, USA, AIAA Paper 1998–2669. American Institute of Aeronautics and Astronautics.CrossRefGoogle Scholar
Ivanov, M., Paciorri, R. & Bonfiglioli, A. 2010 c Numerical simulations of von Neumann reflections. In 40th AIAA Fluid Dynamics Conference and Exhibit, Chicago, IL, USA, AIAA Paper 2010–4859. American Institute of Aeronautics and Astronautics.CrossRefGoogle Scholar
Ivanov, M., Shoev, G., Khotyanovsky, D., Bondar, Ye. & Kudryavtsev, A. 2012 Supersonic patches in steady irregular reflection of weak shock waves. In 28th International Symposium on Shock Waves (ed. K. Kontis), vol. 2, pp. 543–548. Springer.CrossRefGoogle Scholar
Jeffery, G. 1915 The two-dimensional steady motion of a viscous fluid. Phil. Mag. 29, 455–465.CrossRefGoogle Scholar
Jiang, G. & Shu, C. 1996 Efficient implementation of weighted ENO schemes. J. Comput. Phys. 126 (1), 202–228.CrossRefGoogle Scholar
Khotyanovsky, D., Bondar, Ye., Kudryavtsev, A., Shoev, G. & Ivanov, M.S. 2009 Viscous effects in steady reflection of strong shock waves. AIAA J. 47 (5), 1263–1269.CrossRefGoogle Scholar
Kudryavtsev, A. & Khotyanovsky, D. 2005 Numerical investigation of high speed free shear flow instability and Mach wave radiation. Intl J. Aeroacoust. 4 (3), 325–344.CrossRefGoogle Scholar
Liu, H., Chen, H., Zhang, B. & Liu, H. 2019 Effects of Mach number on non-Rankine–Hugoniot shock zone of Mach reflection. J. Spacecr. Rockets 56 (3), 761–770.CrossRefGoogle Scholar
Malkov, E.A., Bondar, Ye.A., Kokhanchik, A.A., Poleshkin, S.O. & Ivanov, M.S. 2015 High-accuracy deterministic solution of the Boltzmann equation for the shock wave structure. Shock Waves 25 (4), 387–397.CrossRefGoogle Scholar
Mölder, S. 2016 Curved shock theory. Shock Waves 26 (4), 337–353.CrossRefGoogle Scholar
von Neumann, J. 1943 Oblique reflection of shocks. Explosive research. Tech. Rep. 12. Bureau of Ordinance.Google Scholar
Sakurai, A. 1964 On the problem of weak Mach reflection. J. Phys. Soc. Japan 19 (8), 1440–1450.CrossRefGoogle Scholar
Sakurai, A., Tsukamoto, M., Khotyanovsky, D. & Ivanov, M. 2011 The flow field near the triple point in steady shock reflection. Shock Waves 21 (3), 267–272.CrossRefGoogle Scholar
Shoev, G.V. & Ivanov, M.S. 2016 Numerical study of shock wave interaction in steady flows of a viscous heat-conducting gas with a low ratio of specific heats. Thermophys. Aeromech. 23 (3), 343–354.CrossRefGoogle Scholar
Shoev, G.V., Timokhin, M.Y. & Bondar, Ye.A. 2020 On the total enthalpy behavior inside a shock wave. Phys. Fluids 32 (4), 041703.CrossRefGoogle Scholar
Sichel, M. 1963 Structure of weak non-Hugoniot shocks. Phys. Fluids 6 (5), 179–206.CrossRefGoogle Scholar
Siegenthaler, A. & Madhani, J. 1998 Experimental verification of departure from Rankine–Hugoniot behaviour in weak Mach reflection. In 13th Australasian Fluid Mechanics Conference, Monash University, Melbourne, Australia, pp. 549–554. Monash University Publishing.Google Scholar
Siegenthaler, A. & Madhani, J. 2001 Outline of a theory of non-Rankine–Hugoniot shock wave in weak Mach reflection. In 14th Australasian Fluid Mechanics Conference, Adelaide University, Adelaide, Australia. (ed. B.B. Dally), pp. 561–564. University of Adelaide.Google Scholar
Skews, B. & Ashworth, J. 2005 The physical nature of weak shock wave reflection. J. Fluid Mech. 542, 105–114.CrossRefGoogle Scholar
Skews, B., Li, G. & Paton, R. 2009 Experiments on Guderley Mach reflection. Shock Waves 19 (2), 95–102.CrossRefGoogle Scholar
Sternberg, J. 1959 Triple-shock-wave intersections. Phys. Fluids 2 (2), 179–206.CrossRefGoogle Scholar
Tan, L.-H., Ren, Y.-X. & Wu, Z.-N. 2006 Analytical and numerical study of the near flow field and shape of the Mach stem in steady flows. J. Fluid Mech. 546, 341–362.CrossRefGoogle Scholar
Tesdall, A. & Hunter, J. 2002 Self-similar solutions for weak shock reflection. SIAM J. Appl. Maths 63 (1), 42–61.CrossRefGoogle Scholar
Tesdall, A., Sanders, R. & Keyfitz, B. 2007 The triple point paradox for the nonlinear wave system. SIAM J. Appl. Maths 67 (2), 321–336.CrossRefGoogle Scholar
Tesdall, A., Sanders, R. & Keyfitz, B. 2008 Self-similar solutions for the triple point paradox in gas dynamics. SIAM J. Appl. Maths 68 (5), 1360–1377.CrossRefGoogle Scholar
Tesdall, A., Sanders, R. & Popivanov, N. 2015 Further results on Guderley Mach reflection and the triple point paradox. J. Sci. Comput. 64 (3), 721–744.CrossRefGoogle Scholar
Vasilev, E. & Kraiko, A. 1999 Numerical simulation of weak shock diffraction over a wedge under the von Neumann paradox conditions. Comput. Math. Math. Phys. 39 (8), 1335–1345.Google Scholar
Vasilev, E. & Olhovskiy, M. 2009 The complex structure of supersonic patches in the steady Mach reflection of the weak shock waves. In Proceedings of the 27th International Symposium on Shock Waves, p. 322.Google Scholar
Vasil'ev, E.I. 2016 The nature of the triple point singularity in the case of stationary reflection of weak shock waves. Fluid Dyn. 51 (6), 804–813.CrossRefGoogle Scholar