Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Vinuesa, R.
Schlatter, P.
and
Nagib, H. M.
2018.
Secondary flow in turbulent ducts with increasing aspect ratio.
Physical Review Fluids,
Vol. 3,
Issue. 5,
Pirozzoli, Sergio
2018.
On turbulent friction in straight ducts with complex cross-section: the wall law and the hydraulic diameter.
Journal of Fluid Mechanics,
Vol. 846,
Issue. ,
Orlandi, Paolo
Modesti, Davide
and
Pirozzoli, Sergio
2018.
DNS of Turbulent Flows in Ducts with Complex Shape.
Flow, Turbulence and Combustion,
Vol. 100,
Issue. 4,
p.
1063.
Kaller, Thomas
Hickel, Stefan
and
Adams, Nikolaus
2018.
LES of an Asymmetrically Heated High Aspect Ratio Duct at High Reynolds Number at Different Wall Temperatures.
Modesti, Davide
Pirozzoli, Sergio
Orlandi, Paolo
and
Grasso, Francesco
2018.
On the role of secondary motions in turbulent square duct flow.
Journal of Fluid Mechanics,
Vol. 847,
Issue. ,
Wang, Yanzhi
Zhao, Yanlin
and
Yao, Jun
2019.
Large eddy simulation of particle deposition and resuspension in turbulent duct flows.
Advanced Powder Technology,
Vol. 30,
Issue. 3,
p.
656.
Owolabi, Bayode
2019.
Characterisation of Turbulent Duct Flows.
p.
7.
Kaller, Thomas
Pasquariello, Vito
Hickel, Stefan
and
Adams, Nikolaus A.
2019.
Turbulent flow through a high aspect ratio cooling duct with asymmetric wall heating.
Journal of Fluid Mechanics,
Vol. 860,
Issue. ,
p.
258.
Léon, Olivier
Méry, Fabien
Piot, Estelle
and
Conte, Claudia
2019.
Near-wall aerodynamic response of an acoustic liner to harmonic excitation with grazing flow.
Experiments in Fluids,
Vol. 60,
Issue. 9,
Dai, Yi-Jun
and
Xu, Chun-Xiao
2019.
Wall pressure and secondary-flow origination in a square duct.
Physics of Fluids,
Vol. 31,
Issue. 8,
Sacco, Francesco
Verzicco, Roberto
and
Ostilla-Mónico, Rodolfo
2019.
Dynamics and evolution of turbulent Taylor rolls.
Journal of Fluid Mechanics,
Vol. 870,
Issue. ,
p.
970.
Gallegos, Ralph Kristoffer B.
and
Sharma, Rajnish N.
2019.
Small flags in rectangular channels: Dynamics and mean wake characteristics.
International Journal of Mechanical Sciences,
Vol. 155,
Issue. ,
p.
518.
Mery, Fabien
Sebbane, Delphine
Roncen, Remi
Piot, Estelle
and
Simon, Frank
2019.
Experimental impedance assessment of innovative liner under shear grazing flow.
Modesti, Davide
Pirozzoli, Sergio
and
Grasso, Francesco
2019.
Direct numerical simulation of developed compressible flow in square ducts.
International Journal of Heat and Fluid Flow,
Vol. 76,
Issue. ,
p.
130.
Nagib, H.M.
Vidal, A.
and
Vinuesa, R.
2019.
Vorticity fluxes: A tool for three-dimensional and secondary flows in turbulent shear flows.
Journal of Fluids and Structures,
Vol. 89,
Issue. ,
p.
39.
Yang, Rui
Wang, Zhen-guo
Zhao, Yu-xin
Wang, Qian-cheng
and
Feng, Wu-heng
2020.
Numerical investigation on spatial development of the secondary flow in a supersonic turbulent square duct.
Aerospace Science and Technology,
Vol. 100,
Issue. ,
p.
105832.
Farooq, Shafqat
Huarte-Espinosa, Martin
and
Ostilla-Mónico, Rodolfo
2020.
Large-scale structures in high-Reynolds-number rotating Waleffe flow.
Journal of Fluid Mechanics,
Vol. 884,
Issue. ,
Iyer, Prahladh S.
and
Malik, Mujeeb R.
2020.
Wall-modeled LES of the NASA Juncture Flow Experiment.
Orlandi, Paolo
and
Pirozzoli, Sergio
2020.
Turbulent flows in square ducts: physical insight and suggestions for turbulence modellers.
Journal of Turbulence,
Vol. 21,
Issue. 2,
p.
106.
Mahmoodi-Jezeh, S. V.
and
Wang, Bing-Chen
2020.
Direct numerical simulation of turbulent flow through a ribbed square duct.
Journal of Fluid Mechanics,
Vol. 900,
Issue. ,
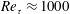 $Re_{\unicode[STIX]{x1D70F}}\approx 1000$). Numerical simulations are carried out over very long integration times to get adequate convergence of the flow statistics, and specifically to achieve high-fidelity representation of the secondary motions which arise. The intensity of the latter is found to be on the order of 1 %–2 % of the bulk velocity, and approximately unaffected by Reynolds number variation, at least in the range under scrutiny. The smallness of the mean convection terms in the streamwise vorticity equation points to a simple characterization of the secondary flows, which in the asymptotic high-
$Re_{\unicode[STIX]{x1D70F}}\approx 1000$). Numerical simulations are carried out over very long integration times to get adequate convergence of the flow statistics, and specifically to achieve high-fidelity representation of the secondary motions which arise. The intensity of the latter is found to be on the order of 1 %–2 % of the bulk velocity, and approximately unaffected by Reynolds number variation, at least in the range under scrutiny. The smallness of the mean convection terms in the streamwise vorticity equation points to a simple characterization of the secondary flows, which in the asymptotic high-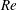 $Re$ regime are approximated with good accuracy by eigenfunctions of the Laplace operator, in the core part of the duct. Despite their effect of redistributing the wall shear stress along the duct perimeter, we find that secondary motions do not have a large influence on the bulk flow properties, and the streamwise velocity field can be characterized with good accuracy as resulting from the superposition of four flat walls in isolation. As a consequence, we find that parametrizations based on the hydraulic diameter concept, and modifications thereof, are successful in predicting the duct friction coefficient.
$Re$ regime are approximated with good accuracy by eigenfunctions of the Laplace operator, in the core part of the duct. Despite their effect of redistributing the wall shear stress along the duct perimeter, we find that secondary motions do not have a large influence on the bulk flow properties, and the streamwise velocity field can be characterized with good accuracy as resulting from the superposition of four flat walls in isolation. As a consequence, we find that parametrizations based on the hydraulic diameter concept, and modifications thereof, are successful in predicting the duct friction coefficient.



