Flow-induced vibration of an elastically mounted sphere was investigated computationally for the classic case where the sphere motion was constrained to move in a direction transverse to the free stream. This study, therefore, provides additional insight into, and comparison with, corresponding experimental studies of transverse motion, and distinction from numerical and experimental studies with specific constraints such as tethering (Williamson & Govardhan, J. Fluids Struct., vol. 11, 1997, pp. 293–305) or motion in all three directions (Behara et al., J. Fluid Mech., vol. 686, 2011, pp. 426–450). Two sets of simulations were conducted by fixing the Reynolds number at 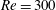$Re=300$ or 800 over the reduced velocity ranges $3.5\leqslant U^{\ast }\leqslant 100$ and $3\leqslant U^{\ast }\leqslant 50$ respectively. The reduced mass of the sphere was kept constant at 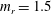$m_{r}=1.5$ for both sets. The flow satisfied the incompressible Navier–Stokes equations, while the coupled sphere motion was modelled by a spring–mass–damper system, with damping set to zero. The sphere showed a highly periodic large-amplitude vortex-induced vibration response over a lower reduced velocity range at both Reynolds numbers considered. This response was designated as branch A, rather than the initial/upper or mode I/II branch, in order to allow it to be discussed independently from the observed experimental response at higher Reynolds numbers which shows both similarities and differences. At 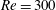$Re=300$, it occurred over the range 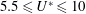$5.5\leqslant U^{\ast }\leqslant 10$, with a maximum oscillation amplitude of ${\approx}0.4D$. On increasing the Reynolds number to 800, this branch widened to cover the range $4.5\leqslant U^{\ast }\leqslant 13$ and the oscillation amplitude increased (maximum amplitude ${\approx}0.6D$). In terms of wake dynamics, within this response branch, two streets of interlaced hairpin-type vortex loops were formed behind the sphere. The upper and lower sets of vortex loops were disconnected, as were their accompanying tails. The wake maintained symmetry relative to the plane defined by the streamwise and sphere motion directions. The topology of this wake structure was analogous to that seen experimentally at higher Reynolds numbers by Govardhan & Williamson (J. Fluid Mech., vol. 531, 2005, pp. 11–47). At even higher reduced velocities, the sphere showed distinct oscillatory behaviour at both Reynolds numbers examined. At 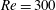$Re=300$, small but non-negligible oscillations were found to occur (amplitude of 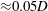${\approx}0.05D$) within the reduced velocity ranges 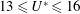$13\leqslant U^{\ast }\leqslant 16$ and $26\leqslant U^{\ast }\leqslant 100$, named branch B and branch C respectively. Moreover, within these reduced velocity ranges, the centre of motion of the sphere shifted from its static position. In contrast, at $Re=800$, the sphere showed an aperiodic intermittent mode IV vibration state immediately beyond branch A, for 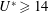$U^{\ast }\geqslant 14$. This vibration state was designated as the intermittent branch. Interestingly, the dominant frequency of the sphere vibration was close to the natural frequency of the system, as observed by Jauvtis et al. (J. Fluids Struct., vol. 15(3), 2001, pp. 555–563) in higher-mass-ratio higher-Reynolds-number experiments. The oscillation amplitude increased as the reduced velocity increased and reached a value of 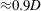${\approx}0.9D$ at 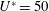$U^{\ast }=50$. The wake was irregular, with multiple vortex shedding cycles during each cycle of sphere oscillation.