Article contents
Translating and squirming cylinders in a viscoplastic fluid
Published online by Cambridge University Press: 06 November 2019
Abstract
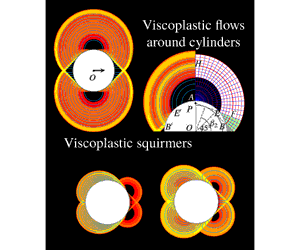
Three related problems of viscoplastic flow around cylinders are considered. First, translating cylinders with no-slip surfaces appear to generate adjacent rotating plugs in the limit where the translation speed becomes vanishingly small. In this plastic limit, analytical results are available from plasticity theory (slipline theory) which indicate that no such plugs should exist. Using a combination of numerical computations and asymptotic analysis, we show that the plugs of the viscoplastic theory actually disappear in the plastic limit, albeit very slowly. Second, when the boundary condition on the cylinder is replaced by one that permits sliding, the plastic limit corresponds to a partially rough cylinder. In this case, no plasticity solution has been previously established; we provide evidence from numerical computations and slipline theory that a previously proposed upper bound (Martin & Randolph, Geotechnique, vol. 56, 2006, pp. 141–145) is actually the true plastic solution. Third, we consider how a prescribed surface velocity field can propel cylindrical squirmers through a viscoplastic fluid. We determine swimming speeds and contrast the results with those from the corresponding Newtonian problem.
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 3
- Cited by




