Article contents
Transition delay in a boundary layer flow using active control
Published online by Cambridge University Press: 15 August 2013
Abstract
Active linear control is applied to delay the onset of laminar–turbulent transition in the boundary layer over a flat plate. The analysis is carried out by numerical simulations of the nonlinear, transitional regime. A three-dimensional, localized initial condition triggering Tollmien–Schlichting waves of finite amplitude is used to numerically simulate the transition to turbulence. Linear quadratic Gaussian controllers based on reduced-order models of the linearized Navier–Stokes equations are designed, where the wall sensors and the actuators are localized in space. A parametric analysis is carried out in the nonlinear regime, for different disturbance amplitudes, by investigating the effects of the actuation on the flow due to different distributions of the localized actuators along the spanwise direction, different sizes of the actuators and the effort of the controllers. We identify the range of parameters where the controllers are effective and highlight the limits of the device for high amplitudes and strong control action. Despite the fully linear control approach, it is shown that the device is effective in delaying the onset of laminar–turbulent transition in the presence of packets characterized by amplitudes 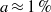 $a\approx 1\hspace{0.167em} \% $ of the free stream velocity at the actuator location. Up to these amplitudes, it is found that a proper choice of the actuators positively affects the performance of the controller. For a transitional case,
$a\approx 1\hspace{0.167em} \% $ of the free stream velocity at the actuator location. Up to these amplitudes, it is found that a proper choice of the actuators positively affects the performance of the controller. For a transitional case, 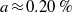 $a\approx 0. 20\hspace{0.167em} \% $, we show a transition delay of
$a\approx 0. 20\hspace{0.167em} \% $, we show a transition delay of 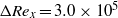 $\Delta {\mathit{Re}}_{x} = 3. 0\times 1{0}^{5} $.
$\Delta {\mathit{Re}}_{x} = 3. 0\times 1{0}^{5} $.
- Type
- Papers
- Information
- Creative Commons
- The online version of this article is published within an Open Access environment subject to the conditions of the Creative Commons Attribution licence .
- Copyright
- ©2013 Cambridge University Press.
References
- 36
- Cited by




