Article contents
Thermal convection with mixed thermal boundary conditions: effects of insulating lids at the top
Published online by Cambridge University Press: 15 March 2017
Abstract
The effects of insulating lids on the convection beneath were investigated experimentally using rectangular convection cells in the flux Rayleigh number range
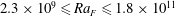 $2.3\times 10^{9}\leqslant Ra_{F}\leqslant 1.8\times 10^{11}$
and cylindrical cells in the range
$2.3\times 10^{9}\leqslant Ra_{F}\leqslant 1.8\times 10^{11}$
and cylindrical cells in the range
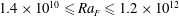 $1.4\times 10^{10}\leqslant Ra_{F}\leqslant 1.2\times 10^{12}$
with the Prandtl number
$1.4\times 10^{10}\leqslant Ra_{F}\leqslant 1.2\times 10^{12}$
with the Prandtl number
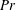 $Pr$
fixed at 4.3. It is found that the presence of the insulating lids leads to reduction of the global heat transfer efficiency as expected, which primarily depends on the insulating area but is insensitive to the detailed insulating patterns. At the leading-order level, the magnitude of temperature fluctuations in the bulk fluid is, again, found to be insensitive to the insulating pattern and mainly depends on the insulating area; while the temperature probability density function in the bulk is essentially invariant with respect to both the insulating area and the spatial pattern of the lids. The flow dynamics, on the other hand, is sensitive to both the covering area and the spatial distribution of the lids. At fixed
$Pr$
fixed at 4.3. It is found that the presence of the insulating lids leads to reduction of the global heat transfer efficiency as expected, which primarily depends on the insulating area but is insensitive to the detailed insulating patterns. At the leading-order level, the magnitude of temperature fluctuations in the bulk fluid is, again, found to be insensitive to the insulating pattern and mainly depends on the insulating area; while the temperature probability density function in the bulk is essentially invariant with respect to both the insulating area and the spatial pattern of the lids. The flow dynamics, on the other hand, is sensitive to both the covering area and the spatial distribution of the lids. At fixed
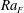 $Ra_{F}$
, the flow strength is found to increase with increasing insulating area so as to transfer the same amount of heat through a smaller cooling area. Moreover, for a constant insulating area, a symmetric insulating pattern results in a symmetric flow pattern, i.e. double-roll structure; whereas an asymmetric insulating pattern leads to asymmetric flow, i.e. single-roll structure. It is further found that the symmetry breaking of the insulating pattern leads to a stronger flow that enhances the horizontal velocity more than the vertical velocity.
$Ra_{F}$
, the flow strength is found to increase with increasing insulating area so as to transfer the same amount of heat through a smaller cooling area. Moreover, for a constant insulating area, a symmetric insulating pattern results in a symmetric flow pattern, i.e. double-roll structure; whereas an asymmetric insulating pattern leads to asymmetric flow, i.e. single-roll structure. It is further found that the symmetry breaking of the insulating pattern leads to a stronger flow that enhances the horizontal velocity more than the vertical velocity.
- Type
- Rapids
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 20
- Cited by





