Hostname: page-component-76fb5796d-dfsvx Total loading time: 0 Render date: 2024-04-26T04:13:28.441Z Has data issue: false hasContentIssue false
  • English
  • Français

Superconvergence of a fully conservative finite difference method on non-uniform staggered grids for simulating wormhole propagation with the Darcy–Brinkman–Forchheimer framework

Published online by Cambridge University Press:  10 June 2019

Xiaoli Li Open the ORCID record for Xiaoli Li [Opens in a new window]  and
Hongxing Rui
Xiaoli Li
Affiliation:
School of Mathematical Sciences and Fujian Provincial Key Laboratory on Mathematical Modelling and High Performance Scientific Computing, Xiamen University, Xiamen, Fujian 361005, China
Hongxing Rui*
Affiliation:
School of Mathematics, Shandong University, Jinan, Shandong 250100, China
*
†Email address for correspondence: hxrui@sdu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, a finite difference scheme on non-uniform staggered grids is proposed for wormhole propagation with the Darcy–Brinkman–Forchheimer framework in porous media by introducing an auxiliary flux variable to guarantee full mass conservation. Error estimates for the pressure, velocity, porosity, concentration and auxiliary flux with second-order superconvergence in different discrete norms are established rigorously and carefully on non-uniform grids. 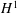We also obtain second-order superconvergence for some terms of the $H^{1}$ norm of the velocity on non-uniform grids. Finally, some numerical experiments are presented to verify the theoretical analysis and effectiveness of the proposed scheme.

JFM classification

Compressible Flows: Compressible boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 872 , 10 August 2019 , pp. 438 - 471
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alazmi, B. & Vafai, K. 2000 Analysis of variants within the porous media transport models. Trans. ASME J. Heat Transfer 122, 303–326.Google Scholar
Arbogast, T., Wheeler, M. F. & Yotov, I. 1997 Mixed finite elements for elliptic problems with tensor coefficients as cell-centered finite differences. SIAM J. Numer. Anal. 34, 828–852.Google Scholar
Fredd, C. N. & Fogler, H. S. 1998 Influence of transport and reaction on wormhole formation in porous media. AIChE J. 44, 1933–1949.Google Scholar
Girault, V. & Lopez, H. 1996 Finite-element error estimates for the MAC scheme. IMA J. Numer. Anal. 16, 347–379.Google Scholar
Girault, V. & Raviart, P.-A. 1979 An analysis of a mixed finite element method for the Navier–Stokes equations. Numer. Math. 33, 235–271.Google Scholar
Girault, V. & Raviart, P.-A. 2012 Finite Element Methods for Navier–Stokes Equations: Theory and Algorithms, vol. 5. Springer Science & Business Media.Google Scholar
Golfier, F., Zarcone, C., Bazin, B., Lenormand, R., Lasseux, D. & Quintard, M. 2002 On the ability of a Darcy-scale model to capture wormhole formation during the dissolution of a porous medium. J. Fluid Mech. 457, 213–254.Google Scholar
Han, H. & Wu, X. 1998 A new mixed finite element formulation and the MAC method for the Stokes equations. SIAM J. Numer. Anal. 35, 560–571.Google Scholar
Kanschat, G. 2008 Divergence-free discontinuous Galerkin schemes for the Stokes equations and the MAC scheme. Intl J. Numer. Meth. Fluids 56, 941–950.Google Scholar
Kladias, N. & Prasad, V. 1991 Experimental verification of Darcy–Brinkman–Forchheimer flow model for natural convection in porous media. J. Thermophys. Heat Transfer 5, 560–576.Google Scholar
Kou, J., Sun, S. & Wu, Y. 2016 Mixed finite element-based fully conservative methods for simulating wormhole propagation. Comput. Meth. Appl. Mech. Engng 298, 279–302.Google Scholar
Li, X. & Rui, H. 2016 A two-grid block-centered finite difference method for nonlinear non-Fickian flow model. Appl. Maths Comput. 281, 300–313.Google Scholar
Li, X. & Rui, H. 2017a Characteristic block-centered finite difference method for simulating incompressible wormhole propagation. Comput. Maths Applics. 73, 2171–2190.Google Scholar
Li, X. & Rui, H. 2017b A two-grid block-centered finite difference method for the nonlinear time-fractional parabolic equation. J. Sci. Comput. 72, 863–891.Google Scholar
Li, X. & Rui, H. 2018a Block-centered finite difference method for simulating compressible wormhole propagation. J. Sci. Comput. 74, 1115–1145.Google Scholar
Li, X. & Rui, H. 2018b Superconvergence of characteristics marker and cell scheme for the Navier–Stokes equations on nonuniform grids. SIAM J. Numer. Anal. 56, 1313–1337.Google Scholar
Liu, M., Zhang, S., Mou, J. & Zhou, F. 2013 Wormhole propagation behavior under reservoir condition in carbonate acidizing. Transp. Porous Med. 96, 203–220.Google Scholar
Liu, W., Cui, J. & Xin, J. 2018 A block-centered finite difference method for an unsteady asymptotic coupled model in fractured media aquifer system. J. Comput. Appl. Maths 337, 319–340.Google Scholar
Minev, P. 2008 Remarks on the links between low-order DG methods and some finite-difference schemes for the Stokes problem. Intl J. Numer. Meth. Fluids 58, 307–318.Google Scholar
Pan, H. & Rui, H. 2012 Mixed element method for two-dimensional Darcy–Forchheimer model. J. Sci. Comput. 52, 563–587.Google Scholar
Panga, M. K., Ziauddin, M. & Balakotaiah, V. 2005 Two-scale continuum model for simulation of wormholes in carbonate acidization. AIChE J. 51, 3231–3248.Google Scholar
Perot, B. 2000 Conservation properties of unstructured staggered mesh schemes. J. Comput. Phys. 159, 58–89.Google Scholar
Perot, J. B. 2011 Discrete conservation properties of unstructured mesh schemes. Annu. Rev. Fluid Mech. 43, 299–318.Google Scholar
Raviart, P.-A. & Thomas, J.-M. 1977 A Mixed Finite Element Method for 2-nd Order Elliptic Problems. Springer.Google Scholar
Rees, D. A. S. 1999 Darcy–Brinkman free convection from a heated horizontal surface. Numer. Heat Transfer 35, 191–204.Google Scholar
Rui, H. & Li, X. 2017 Stability and superconvergence of MAC scheme for Stokes equations on nonuniform grids. SIAM J. Numer. Anal. 55, 1135–1158.Google Scholar
Rui, H. & Pan, H. 2012 A block-centered finite difference method for the Darcy–Forchheimer model. SIAM J. Numer. Anal. 50, 2612–2631.Google Scholar
Rui, H. & Pan, H. 2013 Block-centered finite difference methods for parabolic equation with time-dependent coefficient. Japan J. Indust. Appl. Maths 30, 681–699.Google Scholar
Rui, H., Zhao, D. & Pan, H. 2015 A block-centered finite difference method for Darcy–Forchheimer model with variable Forchheimer number. Numer. Meth. Part. Diff. Equ. 31, 1603–1622.Google Scholar
Vafai, K. & Kim, S. J. 1995 On the limitations of the Brinkman–Forchheimer-extended Darcy equation. Intl J. Heat Fluid Flow 16, 11–15.Google Scholar
Weiser, A. & Wheeler, M. F. 1988 On convergence of block-centered finite differences for elliptic problems. SIAM J. Numer. Anal. 25, 351–375.Google Scholar
Wu, Y., Salama, A. & Sun, S. 2015 Parallel simulation of wormhole propagation with the Darcy–Brinkman–Forchheimer framework. Comput. Geotech. 69, 564–577.Google Scholar
Zhao, C., Hobbs, B., Hornby, P., Ord, A., Peng, S. & Liu, L. 2008 Theoretical and numerical analyses of chemical-dissolution front instability in fluid-saturated porous rocks. Intl J. Numer. Anal. Meth. Geomech. 32, 1107–1130.Google Scholar
Zhao, C., Hobbs, B. E. & Ord, A. 2014 Theoretical analyses of chemical dissolution-front instability in fluid-saturated porous media under non-isothermal conditions. Intl J. Numer. Anal. Meth. Geomech. 102, 799–820.Google Scholar