Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Schnitzer, Ory
and
Yariv, Ehud
2012.
Macroscale description of electrokinetic flows at large zeta potentials: Nonlinear surface conduction.
Physical Review E,
Vol. 86,
Issue. 2,
Schnitzer, Ory
and
Yariv, Ehud
2012.
Induced-charge electro-osmosis beyond weak fields.
Physical Review E,
Vol. 86,
Issue. 6,
Schnitzer, Ory
and
Yariv, Ehud
2012.
Dielectric-solid polarization at strong fields: Breakdown of Smoluchowski's electrophoresis formula.
Physics of Fluids,
Vol. 24,
Issue. 8,
Schnitzer, Ory
Frankel, Itzchak
and
Yariv, Ehud
2013.
Electrokinetic flows about conducting drops.
Journal of Fluid Mechanics,
Vol. 722,
Issue. ,
p.
394.
Schnitzer, Ory
and
Yariv, Ehud
2013.
Comment on “On the flow field about an electrophoretic particle” [Phys. Fluids 24, 102001 (2012)].
Physics of Fluids,
Vol. 25,
Issue. 4,
Schnitzer, Ory
Zeyde, Roman
Yavneh, Irad
and
Yariv, Ehud
2013.
Weakly nonlinear electrophoresis of a highly charged colloidal particle.
Physics of Fluids,
Vol. 25,
Issue. 5,
Figliuzzi, B.
Chan, W. H. R.
Moran, J. L.
and
Buie, C. R.
2014.
Nonlinear electrophoresis of ideally polarizable particles.
Physics of Fluids,
Vol. 26,
Issue. 10,
Schnitzer, Ory
and
Yariv, Ehud
2014.
Nonlinear electrophoresis at arbitrary field strengths: small-Dukhin-number analysis.
Physics of Fluids,
Vol. 26,
Issue. 12,
Schnitzer, Ory
and
Yariv, Ehud
2014.
Strong electro-osmotic flows about dielectric surfaces of zero surface charge.
Physical Review E,
Vol. 89,
Issue. 4,
Schnitzer, Ory
Frankel, Itzchak
and
Yariv, Ehud
2014.
Electrophoresis of bubbles.
Journal of Fluid Mechanics,
Vol. 753,
Issue. ,
p.
49.
Yariv, Ehud
and
Michelin, Sébastien
2015.
Phoretic self-propulsion at large Péclet numbers.
Journal of Fluid Mechanics,
Vol. 768,
Issue. ,
Schnitzer, Ory
and
Yariv, Ehud
2015.
The Taylor–Melcher leaky dielectric model as a macroscale electrokinetic description.
Journal of Fluid Mechanics,
Vol. 773,
Issue. ,
p.
1.
Ghosh, Uddipta
and
Chakraborty, Suman
2016.
Electro-osmosis over inhomogeneously charged surfaces in presence of non-electrostatic ion-ion interactions.
Physics of Fluids,
Vol. 28,
Issue. 6,
Ghosh, Uddipta
Chaudhury, Kaustav
and
Chakraborty, Suman
2016.
Electroosmosis over non-uniformly charged surfaces: modified Smoluchowski slip velocity for second-order fluids.
Journal of Fluid Mechanics,
Vol. 809,
Issue. ,
p.
664.
Navarkar, A.
Amiroudine, S.
Demekhin, E. A.
Ghosh, U.
and
Chakraborty, S.
2016.
Long-wave interface instabilities of a two-layer system under periodic excitation for thin films.
Microfluidics and Nanofluidics,
Vol. 20,
Issue. 11,
Figliuzzi, B.
Chan, W. H. R.
Buie, C. R.
and
Moran, J. L.
2016.
Nonlinear electrophoresis in the presence of dielectric decrement.
Physical Review E,
Vol. 94,
Issue. 2,
Stout, Robert F.
and
Khair, Aditya S.
2017.
Influence of ion sterics on diffusiophoresis and electrophoresis in concentrated electrolytes.
Physical Review Fluids,
Vol. 2,
Issue. 1,
Ghosh, Uddipta
Mandal, Shubhadeep
and
Chakraborty, Suman
2017.
Electroosmosis over charge-modulated surfaces with finite electrical double layer thicknesses: Asymptotic and numerical investigations.
Physical Review Fluids,
Vol. 2,
Issue. 6,
Khair, Aditya S.
2018.
Strong Deformation of the Thick Electric Double Layer around a Charged Particle during Sedimentation or Electrophoresis.
Langmuir,
Vol. 34,
Issue. 3,
p.
876.
Sherwood, J. D.
and
Ghosal, S.
2018.
Nonlinear electrophoresis of a tightly fitting sphere in a cylindrical tube.
Journal of Fluid Mechanics,
Vol. 843,
Issue. ,
p.
847.
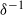 ,
, 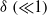 being the dimensionless Debye thickness. The dominant advection associated with the intense flow mandates a uniform salt concentration in the electro-neutral bulk. The
being the dimensionless Debye thickness. The dominant advection associated with the intense flow mandates a uniform salt concentration in the electro-neutral bulk. The  large tangential fields in the diffuse part of the double layer give rise to a novel ‘surface conduction’ mechanism at moderate zeta potentials, where the Dukhin number is vanishingly small. The ensuing
large tangential fields in the diffuse part of the double layer give rise to a novel ‘surface conduction’ mechanism at moderate zeta potentials, where the Dukhin number is vanishingly small. The ensuing 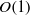 electric current emerging from the double layer modifies the bulk electric field; the comparable
electric current emerging from the double layer modifies the bulk electric field; the comparable  transverse salt flux, on the other hand, is incompatible with the nil diffusive fluxes at the homogeneous bulk. This contradiction is resolved by identifying the emergence of a diffusive boundary layer of
transverse salt flux, on the other hand, is incompatible with the nil diffusive fluxes at the homogeneous bulk. This contradiction is resolved by identifying the emergence of a diffusive boundary layer of 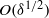 thickness, resembling thermal boundary layers at large-Reynolds-number flows. The modified electric field within the bulk gives rise to an irrotational flow, resembling those in moderate-field electrophoresis. At leading order, the particle electrophoretic velocity is provided by Smoluchowski’s formula, describing linear variation with applied field.
thickness, resembling thermal boundary layers at large-Reynolds-number flows. The modified electric field within the bulk gives rise to an irrotational flow, resembling those in moderate-field electrophoresis. At leading order, the particle electrophoretic velocity is provided by Smoluchowski’s formula, describing linear variation with applied field.



