Article contents
Stratified shear flow: experiments in an inclined duct
Published online by Cambridge University Press: 22 July 2014
Abstract
We present results of experiments on stratified shear flow in an inclined duct. The duct connects two reservoirs of fluid with different densities, and contains a counterflow with a dense layer flowing beneath a less dense layer moving in the opposite direction. We identify four flow states in this experiment, depending on the fractional density differences, characterised by the dimensionless Atwood number, and the angle of inclination  $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\theta $, which is defined to be positive (negative) when the along-duct component of gravity reinforces (opposes) the buoyancy-induced pressure differences across the ends of the duct. For sufficiently negative angles and small fractional density differences, the flow is observed to be laminar (
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\theta $, which is defined to be positive (negative) when the along-duct component of gravity reinforces (opposes) the buoyancy-induced pressure differences across the ends of the duct. For sufficiently negative angles and small fractional density differences, the flow is observed to be laminar ( $\mathsf{L}$ state), with an undisturbed density interface separating the two layers. For positive angles and/or high fractional density differences, three other states are observed. For small angles of inclination, the flow is wave-dominated and exhibits Holmboe modes (
$\mathsf{L}$ state), with an undisturbed density interface separating the two layers. For positive angles and/or high fractional density differences, three other states are observed. For small angles of inclination, the flow is wave-dominated and exhibits Holmboe modes ( $\mathsf{H}$ state) on the interface, with characteristic cusp-like wave breaking. At the highest positive angles and density differences, there is a turbulent (
$\mathsf{H}$ state) on the interface, with characteristic cusp-like wave breaking. At the highest positive angles and density differences, there is a turbulent ( $\mathsf{T}$ state) high-dissipation interfacial region typically containing Kelvin–Helmholtz (KH)-like structures sheared in the direction of the mean shear and connecting both layers. For intermediate angles and density differences, an intermittent state (
$\mathsf{T}$ state) high-dissipation interfacial region typically containing Kelvin–Helmholtz (KH)-like structures sheared in the direction of the mean shear and connecting both layers. For intermediate angles and density differences, an intermittent state ( $\mathsf{I}$ state) is found, which exhibits a rich range of spatio-temporal behaviour and an interfacial region that contains features of KH-like structures and of the other two lower-dissipation states: thin interfaces and Holmboe-like structures. We map the state diagram of these flows in the Atwood number–
$\mathsf{I}$ state) is found, which exhibits a rich range of spatio-temporal behaviour and an interfacial region that contains features of KH-like structures and of the other two lower-dissipation states: thin interfaces and Holmboe-like structures. We map the state diagram of these flows in the Atwood number–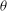 $\theta $ plane and examine the force balances that determine each of these states. We find that the
$\theta $ plane and examine the force balances that determine each of these states. We find that the  $\mathsf{L}$ and
$\mathsf{L}$ and  $\mathsf{H}$ states are hydraulically controlled at the ends of the duct and the flow is determined by the pressure difference associated with the density difference between the reservoirs. As the inclination increases, the along-slope component of the buoyancy force becomes more significant and the
$\mathsf{H}$ states are hydraulically controlled at the ends of the duct and the flow is determined by the pressure difference associated with the density difference between the reservoirs. As the inclination increases, the along-slope component of the buoyancy force becomes more significant and the  $\mathsf{I}$ and
$\mathsf{I}$ and  $\mathsf{T}$ states are associated with increasing dissipation within the duct. We replot the state space in the Grashof number–
$\mathsf{T}$ states are associated with increasing dissipation within the duct. We replot the state space in the Grashof number–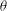 $\theta $ phase plane and find the transition to the
$\theta $ phase plane and find the transition to the  $\mathsf{T}$ state is governed by a critical Grashof number. We find that the corresponding buoyancy Reynolds number of the transition to the
$\mathsf{T}$ state is governed by a critical Grashof number. We find that the corresponding buoyancy Reynolds number of the transition to the  $\mathsf{T}$ state is of the order of 100, and that this state is also found to be hydraulically controlled at the ends of the duct. In this state the dissipation balances the force associated with the along-slope component of buoyancy and the counterflow has a critical composite Froude number.
$\mathsf{T}$ state is of the order of 100, and that this state is also found to be hydraulically controlled at the ends of the duct. In this state the dissipation balances the force associated with the along-slope component of buoyancy and the counterflow has a critical composite Froude number.
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 28
- Cited by




