Hostname: page-component-848d4c4894-mwx4w Total loading time: 0 Render date: 2024-06-27T22:33:35.851Z Has data issue: false hasContentIssue false
  • English
  • Français

Stochastic Lagrangian dynamics of vorticity. Part 2. Application to near-wall channel-flow turbulence

Published online by Cambridge University Press:  19 August 2020

Gregory L. Eyink Open the ORCID record for Gregory L. Eyink [Opens in a new window] ,
Akshat Gupta  and
Tamer A. Zaki Open the ORCID record for Tamer A. Zaki [Opens in a new window]
Gregory L. Eyink*
Affiliation:
Department of Applied Mathematics and Statistics, The Johns Hopkins University, Baltimore, MD21218, USA Department of Physics and Astronomy, The Johns Hopkins University, Baltimore, MD21218, USA Department of Mechanical Engineering, The Johns Hopkins University, Baltimore, MD21218, USA
Akshat Gupta
Affiliation:
Department of Applied Mathematics and Statistics, The Johns Hopkins University, Baltimore, MD21218, USA
Tamer A. Zaki
Affiliation:
Department of Mechanical Engineering, The Johns Hopkins University, Baltimore, MD21218, USA
*
†Email address for correspondence: eyink@jhu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

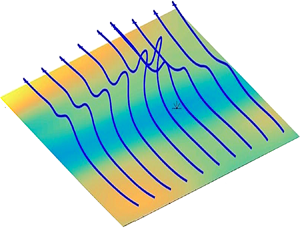
We use an online database of a turbulent channel-flow simulation at $Re_\tau =1000$ (Graham et al. J. Turbul., vol. 17, issue 2, 2016, pp. 181–215) to determine the origin of vorticity in the near-wall buffer layer. Following an experimental study of Sheng et al. (J. Fluid Mech., vol. 633, 2009, pp.17–60), we identify typical ‘ejection’ and ‘sweep’ events in the buffer layer by local minima/maxima of the wall stress. In contrast to their conjecture, however, we find that vortex lifting from the wall is not a discrete event requiring $\sim$1 viscous time and $\sim$10 wall units, but is instead a distributed process over a space–time region at least $1\sim 2$ orders of magnitude larger in extent. To reach this conclusion, we exploit a rigorous mathematical theory of vorticity dynamics for Navier–Stokes solutions, in terms of stochastic Lagrangian flows and stochastic Cauchy invariants, conserved on average backward in time. This theory yields exact expressions for vorticity inside the flow domain in terms of vorticity at the wall, as transported by viscous diffusion and by nonlinear advection, stretching and rotation. We show that Lagrangian chaos observed in the buffer layer can be reconciled with saturated vorticity magnitude by ‘virtual reconnection’: although the Eulerian vorticity field in the viscous sublayer has a single sign of spanwise component, opposite signs of Lagrangian vorticity evolve by rotation and cancel by viscous destruction. Our analysis reveals many unifying features of classical fluids and quantum superfluids. We argue that ‘bundles’ of quantized vortices in superfluid turbulence will also exhibit stochastic Lagrangian dynamics and satisfy stochastic conservation laws resulting from particle relabelling symmetry.

JFM classification

Vortex Flows: Vortex dynamics Turbulent Flows: Turbulent boundary layers Complex Fluids: Quantum fluids
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 901 , 25 October 2020 , A3
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Alamri, S. Z., Youd, A. J. & Barenghi, C. F. 2008 Reconnection of superfluid vortex bundles. Phys. Rev. Lett. 101 (21), 215302.CrossRefGoogle ScholarPubMed
Anderson, P. W. 1966 Considerations on the flow of superfluid helium. Rev. Mod. Phys. 38 (2), 298.CrossRefGoogle Scholar
Andreopoulos, J. & Agui, J. H. 1996 Wall-vorticity flux dynamics in a two-dimensional turbulent boundary layer. J. Fluid Mech. 309, 45–84.CrossRefGoogle Scholar
Baggaley, A. W., Barenghi, C. F., Shukurov, A. & Sergeev, Y. A. 2012 Coherent vortex structures in quantum turbulence. Europhys. Lett. 98 (2), 26002.CrossRefGoogle Scholar
Barenghi, C. F., Skrbek, L. & Sreenivasan, K. R. 2014 Introduction to quantum turbulence. Proc. Natl Acad. Sci. 111 (Supplement 1), 4647–4652.CrossRefGoogle ScholarPubMed
Bernard, D., Gawedzki, K. & Kupiainen, A. 1998 Slow modes in passive advection. J. Stat. Phys. 90 (3–4), 519–569.CrossRefGoogle Scholar
Besse, N. & Frisch, U. 2017 Geometric formulation of the Cauchy invariants for incompressible Euler flow in flat and curved spaces. J. Fluid Mech. 825, 412–478.CrossRefGoogle Scholar
Borodin, A. N. & Salminen, P. 2015 Handbook of Brownian Motion – Facts and Formulae. Birkhäuser.Google Scholar
Brown, G. L. & Roshko, A. 2012 Turbulent shear layers and wakes. J. Turbul. 13, N51.CrossRefGoogle Scholar
Campbell, L. J. 1972 A critical look at a class of critical velocity theories for superfluid He. J. Low Temp. Phys. 8 (1–2), 105–113.CrossRefGoogle Scholar
Cauchy, A. L. 1815 Sur l’état du fluide à une époque quelconque du mouvement. Mémoires extraits des recueils de l'Académie des sciences de l'Institut de France, Théorie de la propagation des ondes à la surface d'un fluide pesant d'une profondeur indéfinie. (Extraits des Mémoires présentés par divers savants à l'Académie royale des Sciences de l'Institut de France et imprimés par son ordre). Sciences mathématiques et physiques. Tome I, 1827 Seconde Partie, pp. 33–73.Google Scholar
Chhikara, R. & Folks, J. L. 1988 The Inverse Gaussian Distribution: Theory: Methodology, and Applications. Taylor & Francis.Google Scholar
Constantin, P. & Iyer, G. 2008 A stochastic Lagrangian representation of the 3-dimensional incompressible Navier–Stokes equations. Commun. Pure Appl. Maths 61, 330–345.CrossRefGoogle Scholar
Constantin, P. & Iyer, G. 2011 A stochastic-Lagrangian approach to the Navier–Stokes equations in domains with boundary. Ann. Appl. Probab. 21 (4), 1466–1492.CrossRefGoogle Scholar
Corrsin, S. 1953 Remarks on turbulent heat transfer. In Proceedings of the Iowa Thermodynamics Symposium, American Society for Engineering Education and Society for the Promotion of Engineering Education (U.S.), vol. 60, pp. 5–30. State University of Iowa.Google Scholar
Crossley, M., Glorioso, P. & Liu, H. 2017 Effective field theory of dissipative fluids. J. High Energy Phys. 2017 (9), 95.CrossRefGoogle Scholar
Drivas, T. D. & Eyink, G. L. 2017 a A Lagrangian fluctuation–dissipation relation for scalar turbulence. Part 1. Flows with no bounding walls. J. Fluid Mech. 829, 153–189.CrossRefGoogle Scholar
Drivas, T. D. & Eyink, G. L. 2017 b A lagrangian fluctuation–dissipation relation for scalar turbulence. Part 2. Wall-bounded flows. J. Fluid Mech. 829, 236–279.CrossRefGoogle Scholar
Eyink, G., Vishniac, E., Lalescu, C., Aluie, H., Kanov, K., Bürger, K., Burns, R., Meneveau, C. & Szalay, A. 2013 Flux-freezing breakdown in high-conductivity magnetohydrodynamic turbulence. Nature 497 (7450), 466–469.CrossRefGoogle ScholarPubMed
Eyink, G. L. 2008 Turbulent flow in pipes and channels as cross-stream ‘inverse cascades’ of vorticity. Phys. Fluids 20 (12), 125101.CrossRefGoogle Scholar
Eyink, G. L. 2010 Stochastic least-action principle for the incompressible Navier–Stokes equation. Physica D 239 (14), 1236–1240.CrossRefGoogle Scholar
Eyink, G. L., Gupta, A. & Zaki, T. A. 2020 Stochastic Lagrangian dynamics of vorticity. Part 1. General theory for viscous, incompressible fluids. J. Fluid Mech. (submitted).Google Scholar
Fuzier, S, Baudouy, B & Van Sciver, S. W. 2001 Steady-state pressure drop and heat transfer in He II forced flow at high Reynolds number. Cryogenics 41 (5–6), 453–458.CrossRefGoogle Scholar
Graham, J., Kanov, K., Yang, X. I. A., Lee, M., Malaya, N., Lalescu, C. C., Burns, R., Eyink, G., Szalay, A., Moser, R. D., et al. 2016 A web services accessible database of turbulent channel flow and its use for testing a new integral wall model for LES. J. Turbul. 17 (2), 181–215.CrossRefGoogle Scholar
Huggins, E. R. 1970 Energy-dissipation theorem and detailed Josephson equation for ideal incompressible fluids. Phys. Rev. A 1 (2), 332.CrossRefGoogle Scholar
Huggins, E. R. 1994 Vortex currents in turbulent superfluid and classical fluid channel flow, the Magnus effect, and Goldstone boson fields. J. Low Temp. Phys. 96 (5–6), 317–346.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
Jiménez, J. 2013 Near-wall turbulence. Phys. Fluids 25 (10), 101302.CrossRefGoogle Scholar
Jimenez, J., Moin, P., Moser, R. & Keefe, L. 1988 Ejection mechanisms in the sublayer of a turbulent channel. Phys. Fluids 31 (6), 1311–1313.CrossRefGoogle Scholar
Johnson, P. L., Hamilton, S. S., Burns, R. & Meneveau, C. 2017 Analysis of geometrical and statistical features of Lagrangian stretching in turbulent channel flow using a database task-parallel particle tracking algorithm. Phys. Rev. Fluids 2 (1), 014605.CrossRefGoogle Scholar
Josephson, B. D. 1962 Possible new effects in superconductive tunnelling. Phys. Lett. 1 (7), 251–253.CrossRefGoogle Scholar
Kedia, H., Kleckner, D., Scheeler, M. W. & Irvine, W. T. M. 2018 Helicity in superfluids: existence and the classical limit. Phys. Rev. Fluids 3 (10), 104702.CrossRefGoogle Scholar
Kim, J. & Hussain, F. 1993 Propagation velocity of perturbations in turbulent channel flow. Phys. Fluids A 5 (3), 695–706.CrossRefGoogle Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.CrossRefGoogle Scholar
Kivotides, D. 2007 Relaxation of superfluid vortex bundles via energy transfer to the normal fluid. Phys. Rev. B 76 (5), 054503.CrossRefGoogle Scholar
Klewicki, J., Fife, P., Wei, T. & McMurtry, P. 2007 A physical model of the turbulent boundary layer consonant with mean momentum balance structure. Phil. Trans. R. Soc. Lond. A 365 (1852), 823–840.CrossRefGoogle ScholarPubMed
Klewicki, J. C., Priyadarshana, P. J. A. & Metzger, M. M. 2008 Statistical structure of the fluctuating wall pressure and its in-plane gradients at high Reynolds number. J. Fluid Mech. 609, 195–220.CrossRefGoogle Scholar
Koplik, J. & Levine, H. 1993 Vortex reconnection in superfluid helium. Phys. Rev. Lett. 71 (9), 1375.CrossRefGoogle ScholarPubMed
Koumoutsakos, P. 1999 Vorticity flux control for a turbulent channel flow. Phys. Fluids 11 (2), 248–250.CrossRefGoogle Scholar
Kuz'min, G. A. 1983 Ideal incompressible hydrodynamics in terms of the vortex momentum density. Phys. Lett. A 96 (2), 88–90.CrossRefGoogle Scholar
Kuz'min, G. A. 1999 Vortex momentum density and invariants of the hydrodynamic equations of superfluidity and superconductivity. Low Temp. Phys. 25 (1), 1–4.CrossRefGoogle Scholar
Lee, M., Malaya, N. & Moser, R. D. 2013 Petascale direct numerical simulation of turbulent channel flow on up to 786 K cores. In SC ’13, Proceedings of the International Conference on High Performance Computing, Networking, Storage and Analysis, Denver, Colorado. ACM.CrossRefGoogle Scholar
Lighthill, M. J. 1963 Boundary layer theory. In Laminar Boundary Layers (ed. L. Rosenhead), pp. 46–113. Oxford University Press.Google Scholar
L'vov, V. S, Nazarenko, S. V. & Rudenko, O. 2007 Bottleneck crossover between classical and quantum superfluid turbulence. Phys. Rev. B 76 (2), 024520.CrossRefGoogle Scholar
Lyman, F. A. 1990 Vorticity production at a solid boundary. Appl. Mech. Rev. 43 (8), 157–158.Google Scholar
Morton, B. R. 1984 The generation and decay of vorticity. Geophys. Astrophys. Fluid Dyn. 28 (3–4), 277–308.CrossRefGoogle Scholar
Natan, A. 2013 Fast 2d peak finder. Matlab File Exchange. Available at: https://www.mathworks.com/matlabcentral/fileexchange/37388-fast-2d-peak-finder.Google Scholar
Nilsen, H. M, Baym, G. & Pethick, C. J. 2006 Velocity of vortices in inhomogeneous Bose–Einstein condensates. Proc. Natl Acad. Sci. 103 (21), 7978–7981.CrossRefGoogle ScholarPubMed
Nore, C., Abid, M. & Brachet, M. E. 1997 Decaying Kolmogorov turbulence in a model of superflow. Phys. Fluids 9 (9), 2644–2669.CrossRefGoogle Scholar
Orszag, S. A. 1971 On the elimination of aliasing in finite-difference schemes by filtering high-wavenumber components. J. Atmos. Sci. 28 (6), 1074–1074.2.0.CO;2>CrossRefGoogle Scholar
Oseledets, V. I. 1989 On a new way of writing the Navier–Stokes equation. The Hamiltonian formalism. Russian Math. Surv. 44 (3), 210.CrossRefGoogle Scholar
Packard, R. E. 1998 The role of the Josephson–Anderson equation in superfluid helium. Rev. Mod. Phys. 70 (2), 641.CrossRefGoogle Scholar
Park, J. S., Shekar, A. & Graham, M. D. 2018 Bursting and critical layer frequencies in minimal turbulent dynamics and connections to exact coherent states. Phys. Rev. Fluids 3 (1), 014611.CrossRefGoogle Scholar
Schwarz, K. W. 1982 Generation of superfluid turbulence deduced from simple dynamical rules. Phys. Rev. Lett. 49 (4), 283.CrossRefGoogle Scholar
Schwarz, K. W. 1988 Three-dimensional vortex dynamics in superfluid He 4: homogeneous superfluid turbulence. Phys. Rev. B 38 (4), 2398.CrossRefGoogle Scholar
Schwarz, K. W. 1990 Phase slip and turbulence in superfluid He 4: a vortex mill that works. Phys. Rev. Lett. 64 (10), 1130.CrossRefGoogle Scholar
Sheng, J., Malkiel, E. & Katz, J. 2009 Buffer layer structures associated with extreme wall stress events in a smooth wall turbulent boundary layer. J. Fluid Mech. 633, 17–60.CrossRefGoogle Scholar
Swanson, C. J., Donnelly, R. J. & Ihas, G. G. 2000 Turbulent pipe flow of He I and He II. Physica B 284, 77–78.CrossRefGoogle Scholar
Taylor, G. I. 1932 The transport of vorticity and heat through fluids in turbulent motion. Proc. R. Soc. Lond. A 135 (828), 685–702.Google Scholar
Taylor, G. I. 1938 Production and dissipation of vorticity in a turbulent fluid. Proc. R. Soc. Lond. A 164 (916), 15–23.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT.CrossRefGoogle Scholar
Tur, A. V. & Yanovsky, V. V. 1993 Invariants in dissipationless hydrodynamic media. J. Fluid Mech. 248, 67–106.CrossRefGoogle Scholar
Varoquaux, E. 2015 Anderson's considerations on the flow of superfluid helium: some offshoots. Rev. Mod. Phys. 87 (3), 803.CrossRefGoogle Scholar
Vinen, W. F. 2000 Classical character of turbulence in a quantum liquid. Phys. Rev. B 61 (2), 1410.CrossRefGoogle Scholar
Waleffe, F. 1998 Three-dimensional coherent states in plane shear flows. Phys. Rev. Lett. 81 (19), 4140.CrossRefGoogle Scholar
Wiegmann, P. 2019 Quantization of hydrodynamics: rotating superfluid and gravitational anomaly. arXiv:1906.03788.CrossRefGoogle Scholar
Xu, T. & Van Sciver, S. W. 2007 Particle image velocimetry measurements of the velocity profile in He II forced flow. Phys. Fluids 19 (7), 071703.CrossRefGoogle Scholar
Zhao, H., Wu, J.-Z. & Luo, J.-S. 2004 Turbulent drag reduction by traveling wave of flexible wall. Fluid Dyn. Res. 34 (3), 175.CrossRefGoogle Scholar

Eyink et al. supplementary movie 1

See pdf file for movie description

Download Eyink et al. supplementary movie 1(Video)
Video 9.8 MB

Eyink et al. supplementary movie 2

See pdf file for movie description

Download Eyink et al. supplementary movie 2(Video)
Video 9.8 MB

Eyink et al. supplementary movie 3

See pdf file for movie description

Download Eyink et al. supplementary movie 3(Video)
Video 3.8 MB

Eyink et al. supplementary movie 4

See pdf file for movie description

Download Eyink et al. supplementary movie 4(Video)
Video 3.6 MB

Eyink et al. supplementary movie 5

See pdf file for movie description

Download Eyink et al. supplementary movie 5(Video)
Video 9.6 MB

Eyink et al. supplementary movie 6

See pdf file for movie description
Download Eyink et al. supplementary movie 6(Video)
Video 10 MB
Supplementary material: PDF

Eyink et al. supplementary material

Supplementary data

Download Eyink et al. supplementary material(PDF)
PDF 124.3 KB
Supplementary material: File

Eyink et al. supplementary material

Supplementary data files

Download Eyink et al. supplementary material(File)
File 1 MB