Hostname: page-component-8448b6f56d-m8qmq Total loading time: 0 Render date: 2024-04-16T09:39:04.848Z Has data issue: false hasContentIssue false
  • English
  • Français

Steady and unsteady modelling of the float height of a rotating air hockey disk

Published online by Cambridge University Press:  30 July 2015

Patrick D. Weidman  and
Michael A. Sprague
Patrick D. Weidman*
Affiliation:
Department of Mechanical Engineering, University of Colorado, Boulder, CO 80309-0427, USA
Michael A. Sprague
Affiliation:
Computational Science Center, National Renewable Energy Laboratory, Golden, CO 80401, USA
*
†Email address for correspondence: weidman@colorado.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

A similarity reduction of the Navier–Stokes equations for the motion of an infinite rotating disk above an air-bearing table yields a coupled pair of ordinary differential equations governed by a Reynolds number 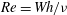$Re=Wh/{\it\nu}$ and a rotation parameter 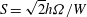$S=\sqrt{2}h{\it\Omega}/W$, where 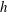$h$ is the float height, 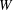$W$ is the air levitation velocity, 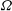${\it\Omega}$ is the disk rotation rate, and ${\it\nu}$ is the kinematic viscosity of air. After deriving the small- and large-Reynolds-number behaviour of solutions, the equations are numerically integrated over a wide range of 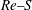$Re{-}S$ parameter space. Zero-lift boundaries are computed as well as the boundaries separating pure outward flow from counter-flow in the gap. The theory is used to model the steady float height of a finite-radius air hockey disk under the assumption that the float height is small relative to the diameter of the disk and the flow is everywhere laminar. The steady results are tested against direct numerical simulation (DNS) of the unsteady axisymmetric Navier–Stokes equations for the cases where the disk rotates at constant angular velocity but is either at a fixed height or free to move axially. While a constant shift in the gap pressure conforms closely to that found using steady theory, the interaction of the radial jet emanating from the gap with a vertical transpiration field produces vortex rings which themselves propagate around to interact with the jet. Although these structures diffuse as they propagate up and away from the gap, they induce a departure from the steady-flow assumption of atmospheric pressure at the gap exit, thus inducing small irregular axial oscillations of the floating disk.

JFM classification

Aerodynamics: Aerodynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 778 , 10 September 2015 , pp. 39 - 59
Copyright
© Cambridge University Press 2015. This is a work of the U.S. Government and is not subject to copyright protection in the United States. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cox, S. M. 2002 Non-axisymmetric flow between an air table and a floating disk. Phys. Fluids 14, 1540–1543.Google Scholar
Dorfman, L. A. 1966 Flow of a viscous fluid between a fixed disk and a flown rotating disk. Izv. Akad. Nauk SSSR Mekh. Zhidk. Gaza 1, 86–91; (Translated to English as NASA TT F-10, 931).Google Scholar
Farkas, Z., Bartels, G., Unger, T. & Wolf, D. E. 2003 Frictional coupling between sliding and spinning motion. Phys. Rev. Lett. 90, 248302.CrossRefGoogle ScholarPubMed
Fischer, P. F. 1997 An overlapping Schwarz method for spectral element solution of the incompressible Navier–Stokes equations. J. Comput. Phys. 133, 84–101.Google Scholar
Hamza, E. A. 1999 Suction and injection effects on a similar flow between parallel plates. J. Phys. D: Appl. Phys. 32, 656–663.CrossRefGoogle Scholar
Hinch, E. J. & Lemaître, J. 1994 The effect of viscosity on the height of disks floating above an air table. J. Fluid Mech. 273, 313–322.Google Scholar
Holodniok, M., Kubicek, M. & Hlavacek, V. 1981 Computation of the flow between two rotating coaxial disks: multiplicity of steady-state solutions. J. Fluid Mech. 108, 227–240.CrossRefGoogle Scholar
Howarth, L. 1951 The boundary layer equations in three dimensional flow. Part II. The flow near a stagnation point. Phil. Mag. 42, 1433–1440.CrossRefGoogle Scholar
Jawa, M. S. 1971 A numerical study of axially symmetric flow between two rotating infinite porous disks. Trans. ASME J. Appl. Mech. 38, 683–687.CrossRefGoogle Scholar
Lance, G. N. & Rogers, M. H. 1962 The axially symmetric flow of a viscous fluid between two infinite rotating disks. Proc. R. Soc. Lond. A 266, 109–121.Google Scholar
Mellor, G. L., Chapple, P. J. & Stokes, V. K. 1968 On the flow between a rotating and a stationary disk. J. Fluid Mech. 31, 95–112.Google Scholar
Nguyen, N. D., Ribault, J. P. & Florent, P. 1975 Multiple solutions for flow between coaxial disks. J. Fluid Mech. 68, 369–388.CrossRefGoogle Scholar
Press, W. H., Flannery, B. P., Teukolosky, S. A. & Vetterling, S. T. 1989 Numerical Recipes. Cambridge University Press.Google Scholar
Saffman, P. G. 1978 The number of waves on unstable vortex rings. J. Fluid Mech. 84, 625–639.Google Scholar
Schlichting, H. 1960 Boundary Layer Theory. McGraw-Hill.Google Scholar
Terrill, R. M. & Cornish, J. P. 1973 Radial flow of a viscous, incompressible fluid between two stationary, uniformly porous discs. Z. Angew. Math. Phys. 24, 676–688.Google Scholar
von Kármán, T. 1921 Über laminare und turbulente Reibung. Z. Angew. Math. Mech. 1, 233–251.CrossRefGoogle Scholar
Wang, C.-Y. 1974 Fluid dynamics of the circular porous slider. Trans. ASME J. Appl. Mech. 41, 343–347.CrossRefGoogle Scholar
Wang, C.-Y. & Watson, L. T. 1979 Viscous flow between rotating discs with injection on the porous disk. Z. Angew. Math. Phys. 30, 773–786.CrossRefGoogle Scholar
Weidman, P. D. & Malhotra, C. P. 2005 Regimes of terminal motion of sliding spinning disks. Phys. Rev. Lett. 95, 264303.CrossRefGoogle ScholarPubMed
Weidman, P. D. & Malhotra, C. 2007 On the terminal motion of sliding spinning disks with uniform Coulomb friction. Physica D 233, 1–13.CrossRefGoogle Scholar
Zandbergen, P. J. & Dijkstra, D. 1987 von Kármán swirling flows. Annu. Rev. Fluid Mech. 19, 465–491.Google Scholar