Hostname: page-component-848d4c4894-sjtt6 Total loading time: 0 Render date: 2024-06-24T00:56:40.730Z Has data issue: false hasContentIssue false
  • English
  • Français

Solute dispersion in pulsatile Casson fluid flow in a tube with wall absorption

Published online by Cambridge University Press:  23 March 2016

Jyotirmoy Rana  and
P. V. S. N. Murthy
Jyotirmoy Rana*
Affiliation:
Department of Mathematics, Indian Institute of Technology, Kharagpur 721302, India
P. V. S. N. Murthy
Affiliation:
Department of Mathematics, Indian Institute of Technology, Kharagpur 721302, India
*
†Email address for correspondence: jyotirmoy.rana@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

The analysis of axial dispersion of solute is presented in a pulsatile flow of Casson fluid through a tube in the presence of interfacial mass transport due to irreversible first-order reaction catalysed by the tube wall. The theory of dispersion is studied by employing the generalized dispersion model proposed by Sankarasubramanian & Gill (Proc. R. Soc. Lond. A, vol. 333 (1592), 1973, pp. 115–132). This dispersion model describes the whole dispersion process in terms of three effective transport coefficients, i.e. exchange, convection and dispersion coefficients. In the present study, the effects of yield stress of Casson fluid 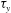${\it\tau}_{y}$, wall absorption parameter 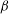${\it\beta}$, amplitude of fluctuating pressure component $e$ and Womersley frequency parameter ${\it\alpha}$ on the dispersion process are discussed under the influence of pulsatile pressure gradient. In a pulsatile flow, the plug flow radius changes during the period of oscillation and it has an effect on the dispersion process. Even with the Casson fluid model also, in an oscillatory flow, for small values of ${\it\alpha}$, the dispersion coefficient 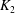$K_{2}$ is positive, but when the value of ${\it\alpha}$ is as large as 3, 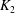$K_{2}$ takes both positive and negative values due to the fluctuations in the velocity profiles. This nature becomes more predominant for 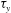${\it\tau}_{y}$, $e$ and 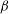${\it\beta}$. It is observed that initially, for small time, the amplitude and magnitude of fluctuations of 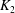$K_{2}$ becomes more rapid and increases with time but it decreases after certain time and reaches a non-transient state for large time. Like in the case of Newtonian model, double frequency period for 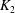$K_{2}$ is observed at small time for large values of ${\it\alpha}$ with the Casson model for blood. It is seen that critical time for which 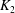$K_{2}$ reaches a non-transient state is independent of 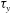${\it\tau}_{y}$ and $e$ but is dependent on ${\it\alpha}$. It is also observed that the axial distribution of mean concentration $C_{m}$ of solute depends on 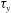${\it\tau}_{y}$ and 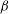${\it\beta}$. But the effect of $e$ and ${\it\alpha}$ on 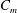$C_{m}$ is not very significant. This dispersion model in non-Newtonian pulsatile flow can be applied to study the dispersion process in the cardiovascular system and blood oxygenators.

JFM classification

Biological Fluid Dynamics: Blood flow Non-Newtonian Flows: Rheology
Type
Papers
Information
Journal of Fluid Mechanics , Volume 793 , 25 April 2016 , pp. 877 - 914
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agrawal, S. & Jayaraman, G. 1994 Numerical simulation of dispersion in the flow of power law fluids in curved tubes. Appl. Math. Model. 18 (9), 504–512.Google Scholar
Aris, R. 1956 On the dispersion of a solute in a fluid flowing through a tube. Proc. R. Soc. Lond. A 235 (1200), 67–77.Google Scholar
Aris, R. 1960 On the dispersion of a solute in pulsating flow through a tube. Proc. R. Soc. Lond. A 259 (1298), 370–376.Google Scholar
Aroesty, J. & Gross, J. F. 1972 The mathematics of pulsatile flow in small vessels: I. Casson theory. Microvasc. Res. 4 (1), 1–12.Google Scholar
Bandyopadhyay, S. & Mazumder, B. S. 1999 Unsteady convective diffusion in a pulsatile flow through a channel. Acta Mechanica 134 (1–2), 1–16.CrossRefGoogle Scholar
Boyce, W. E, DiPrima, R. C. & Haines, C. W. 1992 Elementary Differential Equations and Boundary Value Problems. Wiley.Google Scholar
Bronzino, J. D. 1999 Biomedical Engineering Handbook. CRC Press.Google Scholar
Caro, C. G., Pedley, T. J., Schroter, R. C. & Seed, W. A. 1978 The Mechanics of the Circulation. Oxford University Press.Google Scholar
Chandran, K. B., Rittgers, S. E. & Yoganathan, A. P. 2012 Biofluid Mechanics: The Human Circulation. CRC Press.Google Scholar
Chatwin, P. C. 1975 On the longitudinal dispersion of passive contaminant in oscillatory flows in tubes. J. Fluid Mech. 71 (03), 513–527.Google Scholar
Craciunescu, O. I. & Clegg, S. T. 2001 Pulsatile blood flow effects on temperature distribution and heat transfer in rigid vessels. J. Biomech. Engng 123 (5), 500–505.CrossRefGoogle ScholarPubMed
Dash, R. K., Jayaraman, G. & Mehta, K. N. 1996 Estimation of increased flow resistance in a narrow catheterized artery – a theoretical model. J. Biomech. 29 (7), 917–930.CrossRefGoogle Scholar
Dash, R. K., Jayaraman, G. & Mehta, K. N. 2000 Shear augmented dispersion of a solute in a Casson fluid flowing in a conduit. Ann. Biomed. Engng 28 (4), 373–385.Google Scholar
Gill, W. N. & Sankarasubramanian, R. 1970 Exact analysis of unsteady convective diffusion. Proc. R. Soc. Lond. A 316 (1526), 341–350.Google Scholar
Hazra, S. B., Gupta, A. S. & Niyogi, P. 1997 On the dispersion of a solute in oscillating flow of a non-newtonian fluid in a channel. Heat Mass Transfer 32 (6), 481–488.Google Scholar
Joshi, C. H., Kamm, R. D., Drazen, J. M. & Slutsky, A. S. 1983 An experimental study of gas exchange in laminar oscillatory flow. J. Fluid Mech. 133, 245–254.CrossRefGoogle Scholar
Kaye, S. R., Kavafyan, P. & Schroter, R. C. 1993 Dispersion and uptake in a coiled tube. J. Biomech. Engng 115 (1), 125–126.Google Scholar
Ku, D. N. 1997 Blood flow in arteries. Annu. Rev. Fluid Mech. 29 (1), 399–434.Google Scholar
Kumar, S. & Jayaraman, G. 2008 Method of moments for laminar dispersion in an oscillatory flow through curved channels with absorbing walls. Heat Mass Transfer 44 (11), 1323–1336.Google Scholar
Mazumder, B. S. & Das, S. K. 1992 Effect of boundary reaction on solute dispersion in pulsatile flow through a tube. J. Fluid Mech. 239, 523–549.CrossRefGoogle Scholar
Mazumder, B. S. & Mondal, K. K. 2005 On solute transport in oscillatory flow through an annular pipe with a reactive wall and its application to a catheterized artery. Q. J. Mech. Appl. Maths 58 (3), 349–365.Google Scholar
Merrill, E. W. 1969 Rheology of blood. Phys. Rev. 49 (4), 863–888.Google Scholar
Nagarani, P., Sarojamma, G. & Jayaraman, G. 2004 Effect of boundary absorption in dispersion in Casson fluid flow in a tube. Ann. Biomed. Engng 32 (5), 706–719.Google Scholar
Nagarani, P., Sarojamma, G. & Jayaraman, G. 2006 Exact analysis of unsteady convective diffusion in Casson fluid flow in an annulus–application to catheterized artery. Acta Mechanica 187 (1–4), 189–202.Google Scholar
Nagarani, P., Sarojamma, G. & Jayaraman, G. 2009 Effect of boundary absorption on dispersion in Casson fluid flow in an annulus: application to catheterized artery. Acta Mechanica 202 (1–4), 47–63.Google Scholar
Nagarani, P. & Sebastian, B. T. 2013 Dispersion of a solute in pulsatile non-newtonian fluid flow through a tube. Acta Mechanica 224 (3), 571–585.CrossRefGoogle Scholar
Ng, C. O. 2006 Dispersion in steady and oscillatory flows through a tube with reversible and irreversible wall reactions. Proc. R. Soc. Lond. A 462 (2066), 481–515.Google Scholar
Paul, S. 2011 Effect of wall oscillation on dispersion in axi-symmetric flows between two coaxial cylinders. Z. Angew. Math. Mech. 91 (1), 23–37.Google Scholar
Rao, A. R. & Deshikachar, K. S. 1987 An exact analysis of unsteady convective diffusion in an annular pipe. Z. Angew. Math. Mech. 67 (3), 189–195.Google Scholar
Sankarasubramanian, R. & Gill, W. N. 1973 Unsteady convective diffusion with interphase mass transfer. Proc. R. Soc. Lond. A 333 (1592), 115–132.Google Scholar
Sarkar, A. & Jayaraman, G. 2004 The effect of wall absorption on dispersion in oscillatory flow in an annulus: application to a catheterized artery. Acta Mechanica 172 (3–4), 151–167.CrossRefGoogle Scholar
Sebastian, B. T. & Nagarani, P. 2015 Effect of boundary absorption on dispersion of a solute in pulsatile Casson fluid flow. Interdiscip. Top. Appl. Math. Model. Comput. Sci. 389–395.Google Scholar
Sharp, M. K. 1993 Shear-augmented dispersion in non-newtonian fluids. Ann. Biomed. Engng 21 (4), 407–415.Google Scholar
Smith, R. 1982 Contaminant dispersion in oscillatory flows. J. Fluid Mech. 114, 379–398.Google Scholar
Taylor, G. 1953 Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. A 219 (1137), 186–203.Google Scholar
Truskey, G. A., Yuan, F. & Katz, D. F. 2004 Transport Phenomena in Biological Systems. Pearson Prentice Hall.Google Scholar