Hostname: page-component-848d4c4894-hfldf Total loading time: 0 Render date: 2024-05-14T06:14:49.867Z Has data issue: false hasContentIssue false
  • English
  • Français

Shock–contact–shock solutions of the Riemann problem for dilute granular gas

Published online by Cambridge University Press:  15 March 2021

Yahia M. Fouda Open the ORCID record for Yahia M. Fouda [Opens in a new window]
Yahia M. Fouda*
Affiliation:
Department of Mechanical Power Engineering, Faculty of Engineering, Mansoura University, Mansoura35516, Egypt
*
†Email address for correspondence: yahia_fouda@mans.edu.eg
Get access Rights & Permissions [Opens in a new window]

Abstract

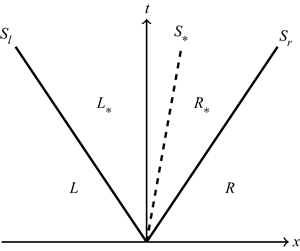
This paper presents an analytical study of the Riemann problem for dilute granular gas using initial conditions that result in a shock–contact–shock wave structure. The Euler equations for molecular gas were perturbed with small granular energy dissipation, resulting in an approximate analytical solution that is valid for early evolution time. This approximate analytical solution shows good agreement with the numerical solution of the full problem obtained using a shock-capturing scheme. It is shown that the wave structure of the Riemann problem for dilute granular gas follows that of molecular gas. However, the variables in regions between the discontinuities are functions of both space and time. Our solution shows that the ‘density overshoot’ – reported by Reddy & Alam (J. Fluid Mech., vol. 779, 2015, R2) – is not part of the shock layer but a signature of the density variation in the star region between the left and right shocks, with the maximum density occurring at the contact discontinuity.

JFM classification

Granular media: Granular media Compressible Flows: Shock waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 915 , 25 May 2021 , A48
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Almazán, L., Serero, D., Salueña, C. & Pöschel, T. 2015 Self-organized shocks in the sedimentation of a granular gas. Phys. Rev. E 91 (6), 062214.CrossRefGoogle ScholarPubMed
Almazán, L., Serero, D., Salueña, C. & Pöschel, T. 2017 Energy decay in a granular gas collapse. New J. Phys. 19 (1), 013001.CrossRefGoogle Scholar
Aursand, P., Evje, S., Flåtten, T., Giljarhus, K.E.T. & Munkejord, S.T. 2014 An exponential time-differencing method for monotonic relaxation systems. Appl. Numer. Maths 80, 1–21.CrossRefGoogle Scholar
Campbell, C.S. 1990 Rapid granular flows. Annu. Rev. Fluid Mech. 22 (1), 57–90.CrossRefGoogle Scholar
Campbell, C.S. 2006 Granular material flows–an overview. Powder Technol. 162 (3), 208–229.CrossRefGoogle Scholar
Esipov, S.E. & Pöschel, T. 1997 The granular phase diagram. J. Stat. Phys. 86 (5–6), 1385–1395.CrossRefGoogle Scholar
Goldhirsch, I. 2003 Rapid granular flows. Annu. Rev. Fluid Mech. 35 (1), 267–293.CrossRefGoogle Scholar
Goldhirsch, I. 2008 Introduction to granular temperature. Powder Technol. 182 (2), 130–136.CrossRefGoogle Scholar
Goldshtein, A., Alexeev, A. & Shapiro, M. 2003 Shock waves in granular gases. In Granular Gas Dynamics, pp. 187–225. Springer.CrossRefGoogle Scholar
Goldshtein, A., Kamenetsky, V., Potapov, A., Shapiro, M., Campbell, C. & Degani, D. 2002 Hydrodynamics of rapid granular flow of inelastic particles into vacuum. Granul. Matt. 4 (3), 115–127.CrossRefGoogle Scholar
Goldshtein, A. & Shapiro, M. 1995 Mechanics of collisional motion of granular materials. Part 1. General hydrodynamic equations. J. Fluid Mech. 282, 75–114.CrossRefGoogle Scholar
Goldshtein, A., Shapiro, M. & Gutfinger, C. 1996 a Mechanics of collisional motion of granular materials. Part 3. Self-similar shock wave propagation. J. Fluid Mech. 316, 29–51.CrossRefGoogle Scholar
Goldshtein, A., Shapiro, M. & Gutfinger, C. 1996 b Mechanics of collisional motion of granular materials. Part 4. Expansion wave. J. Fluid Mech. 327, 117–138.CrossRefGoogle Scholar
Heil, P., Rericha, E.C., Goldman, D.I. & Swinney, H.L. 2004 Mach cone in a shallow granular fluid. Phys. Rev. E 70 (6), 060301.CrossRefGoogle Scholar
Jenkins, J.T. & Richman, M.W. 1985 Kinetic theory for plane flows of a dense gas of identical, rough, inelastic, circular disks. Phys. Fluids 28 (12), 3485–3494.CrossRefGoogle Scholar
Jin, S. & Xin, Z. 1995 The relaxation schemes for systems of conservation laws in arbitrary space dimensions. Commun. Pure Appl. Maths 48 (3), 235–276.CrossRefGoogle Scholar
Kamath, H. & Du, X. 2009 A roe-average algorithm for a granular-gas model with non-conservative terms. J. Comput. Phys. 228 (21), 8187–8202.CrossRefGoogle Scholar
Kamenetsky, V., Goldshtein, A., Shapiro, M. & Degani, D. 2000 Evolution of a shock wave in a granular gas. Phys. Fluids 12 (11), 3036–3049.CrossRefGoogle Scholar
Khan, A., Verma, S., Hankare, P., Kumar, R. & Kumar, S. 2020 Shock–shock interactions in granular flows. J. Fluid Mech. 884, R4.CrossRefGoogle Scholar
LeVeque, R.J. 2002 Finite Volume Methods for Hyperbolic Problems. Cambridge University Press.CrossRefGoogle Scholar
Matveev, S.K. 1983 Model of a gas of solid particles with allowance for inelastic collisions. Fluid Dyn. 18 (6), 839–843.CrossRefGoogle Scholar
Padgett, D.A., Mazzoleni, A.P. & Faw, S.D. 2015 Survey of shock-wave structures of smooth-particle granular flows. Phys. Rev. E 92 (6), 062209.CrossRefGoogle ScholarPubMed
Pareschi, L. & Russo, G. 2005 Implicit–explicit Runge–Kutta schemes and applications to hyperbolic systems with relaxation. J. Sci. Comput. 25 (1), 129–155.Google Scholar
Reddy, M.H.L. & Alam, M. 2015 Plane shock waves and Haff's law in a granular gas. J. Fluid Mech. 779, R2.CrossRefGoogle Scholar
Reddy, M.H.L. & Alam, M. 2016 Plane shock wave structure in a dilute granular gas. AIP Conf. Proc. 1786 (1), 120001.CrossRefGoogle Scholar
Reddy, M.H.L. & Alam, M. 2020 Regularized extended-hydrodynamic equations for a rarefied granular gas and the plane shock waves. Phys. Rev. Fluids 5 (4), 044302.CrossRefGoogle Scholar
Reddy, M.H.L., Ansumali, S. & Alam, M. 2014 Shock waves in a dilute granular gas. AIP Conf. Proc. 1628 (1), 480–487.CrossRefGoogle Scholar
Rericha, E.C., Bizon, C., Shattuck, M.D. & Swinney, H.L. 2001 Shocks in supersonic sand. Phys. Rev. Lett. 88 (1), 014302.CrossRefGoogle ScholarPubMed
Serna, S. & Marquina, A. 2005 Capturing shock waves in inelastic granular gases. J. Comput. Phys. 209 (2), 787–795.CrossRefGoogle Scholar
Serna, S. & Marquina, A. 2007 Capturing blast waves in granular flow. Comput. Fluids 36 (8), 1364–1372.CrossRefGoogle Scholar
Sirmas, N. & Radulescu, M.I. 2015 Evolution and stability of shock waves in dissipative gases characterized by activated inelastic collisions. Phys. Rev. E 91 (2), 023003.CrossRefGoogle ScholarPubMed
Sirmas, N. & Radulescu, M.I. 2019 Structure and stability of shock waves in granular gases. J. Fluid Mech. 873, 568–607.CrossRefGoogle Scholar
Sirmas, N., Tudorache, M., Barahona, J. & Radulescu, M.I. 2012 Shock waves in dense hard disk fluids. Shock Waves 22 (3), 237–247.CrossRefGoogle Scholar
Soleymani, A., Zamankhan, P. & Polashenski, W. 2004 Supersonic dense granular materials in a duct flow. Appl. Phys. Lett. 84 (22), 4409–4411.CrossRefGoogle Scholar
Tan, M.-L. & Goldhirsch, I. 1998 Rapid granular flows as mesoscopic systems. Phys. Rev. Lett. 81, 3022–3025.CrossRefGoogle Scholar
Toro, E.F. 2013 Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction. Springer Science & Business Media.Google Scholar
Wassgren, C.R., Cordova, J.A., Zenit, R. & Karion, A. 2003 Dilute granular flow around an immersed cylinder. Phys. Fluids 15 (11), 3318–3330.CrossRefGoogle Scholar