Article contents
A second-order integral model for buoyant jets with background homogeneous and isotropic turbulence
Published online by Cambridge University Press: 20 May 2019
Abstract
Buoyant jets or forced plumes are discharged into a turbulent ambient in many natural and engineering applications. The background turbulence generally affects the mixing characteristics of the buoyant jet, and the extent of the influence depends on the characteristics of both the jet discharge and ambient. Previous studies focused on the experimental investigation of the problem (for pure jets or plumes), but the findings were difficult to generalize because suitable scales for normalization of results were not known. A model to predict the buoyant jet mixing in the presence of background turbulence, which is essential in many applications, is also hitherto not available even for a background of homogeneous and isotropic turbulence (HIT). We carried out experimental and theoretical investigations of a buoyant jet discharging into background HIT. Buoyant jets were designed to be in the range of 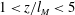 $1<z/l_{M}<5$, where
$1<z/l_{M}<5$, where 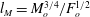 $l_{M}=M_{o}^{3/4}/F_{o}^{1/2}$ is the momentum length scale, with
$l_{M}=M_{o}^{3/4}/F_{o}^{1/2}$ is the momentum length scale, with 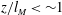 $z/l_{M}<\sim 1$ and
$z/l_{M}<\sim 1$ and 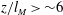 $z/l_{M}>\sim 6$ representing the asymptotic cases of pure jets and plumes, respectively. The background turbulence was generated using a random synthetic jet array, which produced a region of approximately isotropic and homogeneous field of turbulence to be used in the experiments. The velocity scale of the jet was initially much higher, and the length scale smaller, than that of the background turbulence, which is typical in most applications. Comprehensive measurements of the buoyant jet mixing characteristics were performed up to the distance where jet breakup occurred. Based on the experimental findings, a critical length scale
$z/l_{M}>\sim 6$ representing the asymptotic cases of pure jets and plumes, respectively. The background turbulence was generated using a random synthetic jet array, which produced a region of approximately isotropic and homogeneous field of turbulence to be used in the experiments. The velocity scale of the jet was initially much higher, and the length scale smaller, than that of the background turbulence, which is typical in most applications. Comprehensive measurements of the buoyant jet mixing characteristics were performed up to the distance where jet breakup occurred. Based on the experimental findings, a critical length scale 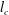 $l_{c}$ was identified to be an appropriate normalizing scale. The momentum flux of the buoyant jet in background HIT was found to be conserved only if the second-order turbulence statistics of the jet were accounted for. A general integral jet model including the background HIT was then proposed based on the conservation of mass (using the entrainment assumption), total momentum and buoyancy fluxes, and the decay function of the jet mean momentum downstream. Predictions of jet mixing characteristics from the new model were compared with experimental observation, and found to be generally in agreement with each other.
$l_{c}$ was identified to be an appropriate normalizing scale. The momentum flux of the buoyant jet in background HIT was found to be conserved only if the second-order turbulence statistics of the jet were accounted for. A general integral jet model including the background HIT was then proposed based on the conservation of mass (using the entrainment assumption), total momentum and buoyancy fluxes, and the decay function of the jet mean momentum downstream. Predictions of jet mixing characteristics from the new model were compared with experimental observation, and found to be generally in agreement with each other.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 13
- Cited by




