Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Fernández-Cabán, Pedro L.
Masters, Forrest J.
and
Phillips, Brian M.
2018.
Predicting Roof Pressures on a Low-Rise Structure From Freestream Turbulence Using Artificial Neural Networks.
Frontiers in Built Environment,
Vol. 4,
Issue. ,
Moore, D. M.
Letchford, C. W.
and
Amitay, M.
2019.
Proceedings of the XV Conference of the Italian Association for Wind Engineering.
Vol. 27,
Issue. ,
p.
519.
Moore, D. M.
Letchford, C. W.
and
Amitay, M.
2019.
Energetic scales in a bluff body shear layer.
Journal of Fluid Mechanics,
Vol. 875,
Issue. ,
p.
543.
Launay, Gaby
Mignot, Emmanuel
and
Rivière, Nicolas
2019.
Laminar free-surface flow around emerging obstacles: Role of the obstacle elongation on the horseshoe vortex.
European Journal of Mechanics - B/Fluids,
Vol. 77,
Issue. ,
p.
71.
Cao, Yong
Tamura, Tetsuro
and
Kawai, Hidenori
2020.
Spanwise resolution requirements for the simulation of high-Reynolds-number flows past a square cylinder.
Computers & Fluids,
Vol. 196,
Issue. ,
p.
104320.
Nguyen, T.
Vaghetto, R.
and
Hassan, Y.
2020.
Experimental investigation of turbulent wake flows in a helically wrapped rod bundle in presence of localized blockages.
Physics of Fluids,
Vol. 32,
Issue. 7,
Fernández-Cabán, Pedro L.
and
Masters, Forrest J.
2020.
Experiments in a Large Boundary Layer Wind Tunnel: Upstream Terrain Effects on Surface Pressures Acting on a Low-Rise Structure.
Journal of Structural Engineering,
Vol. 146,
Issue. 8,
Moore, D.M.
and
Amitay, M.
2021.
Production and migration of turbulent kinetic energy in bluff body shear layers.
International Journal of Heat and Fluid Flow,
Vol. 88,
Issue. ,
p.
108716.
Lysenko, D.A.
and
Ertesvåg, I.S.
2021.
Assessment of algebraic subgrid scale models for the flow over a triangular cylinder at Re = 45000.
Ocean Engineering,
Vol. 222,
Issue. ,
p.
108559.
Muyshondt, Robert
Nguyen, Thien
Hassan, Y. A.
and
Anand, N. K.
2021.
Experimental Measurements of the Wake of a Sphere at Subcritical Reynolds Numbers.
Journal of Fluids Engineering,
Vol. 143,
Issue. 6,
Wang, Wei
Cao, Yong
and
Okaze, Tsubasa
2021.
Comparison of hexahedral, tetrahedral and polyhedral cells for reproducing the wind field around an isolated building by LES.
Building and Environment,
Vol. 195,
Issue. ,
p.
107717.
Lysenko, Dmitry A.
Donskov, Mark
and
Ertesvåg, Ivar S.
2021.
Large-eddy simulations of the flow over a semi-circular cylinder at Re = 50000.
Computers & Fluids,
Vol. 228,
Issue. ,
p.
105054.
Zaldivar de Alba, Antonio
Lombardo, Franklin T.
Lopez, Jason M.
and
Nevill, Justin B.
2021.
Development and validation of a mobile bluff-body to understand extreme wind loading.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 210,
Issue. ,
p.
104504.
Fang, Xingjun
Tachie, Mark F.
and
Bergstrom, Donald J.
2021.
Direct numerical simulation of turbulent flow separation induced by a forward-facing step.
International Journal of Heat and Fluid Flow,
Vol. 87,
Issue. ,
p.
108753.
Zhao, Chongyu
Wang, Hanfeng
Zeng, Lingwei
Alam, Md. Mahbub
and
Zhao, Xiaoyan
2021.
Effects of oncoming flow turbulence on the near wake and forces of a 3D square cylinder.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 214,
Issue. ,
p.
104674.
Li, Cruz Y.
Chen, Zengshun
Lin, Xisheng
Weerasuriya, Asiri Umenga
Zhang, Xuelin
Fu, Yunfei
and
Tse, Tim K. T.
2022.
The linear-time-invariance notion to the Koopman analysis: The architecture, pedagogical rendering, and fluid–structure association.
Physics of Fluids,
Vol. 34,
Issue. 12,
Li, Cruz Y.
Chen, Zengshun
Tse, Tim K. T.
Weerasuriya, Asiri U.
Zhang, Xuelin
Fu, Yunfei
and
Lin, Xisheng
2022.
A parametric and feasibility study for data sampling of the dynamic mode decomposition: range, resolution, and universal convergence states.
Nonlinear Dynamics,
Vol. 107,
Issue. 4,
p.
3683.
Fang, Xingjun
Tachie, Mark F.
and
Dow, Karen
2022.
Turbulent separations beneath semi-submerged bluff bodies with smooth and rough undersurfaces.
Journal of Fluid Mechanics,
Vol. 947,
Issue. ,
Forouzi Feshalami, Behzad
He, Shuisheng
Scarano, Fulvio
Gan, Lian
and
Morton, Chris
2022.
A review of experiments on stationary bluff body wakes.
Physics of Fluids,
Vol. 34,
Issue. 1,
Li, Cruz Y.
Chen, Zengshun
Tse, Tim K. T.
Weerasuriya, Asiri Umenga
Zhang, Xuelin
Fu, Yunfei
and
Lin, Xisheng
2022.
A parametric and feasibility study for data sampling of the dynamic mode decomposition: Spectral insights and further explorations.
Physics of Fluids,
Vol. 34,
Issue. 3,
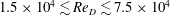 $1.5\times 10^{4}\lesssim Re_{D}\lesssim 7.5\times 10^{4}$. It was found that the ratio between the shear layer frequency and the shedding frequency obeys a power-law scaling relation. Adherence to the power-law relationship, which was derived from hot-wire measurements, has been supported by two additional and independent scaling considerations, namely, by particle image velocimetry measurements to observe the evolution of length and velocity scales in the shear layer during transition, and by comparison to direct numerical simulations to illuminate the properties of the front-face boundary layer. The nonlinear dependence of the shear layer instability frequency is sustained by the influence of
$1.5\times 10^{4}\lesssim Re_{D}\lesssim 7.5\times 10^{4}$. It was found that the ratio between the shear layer frequency and the shedding frequency obeys a power-law scaling relation. Adherence to the power-law relationship, which was derived from hot-wire measurements, has been supported by two additional and independent scaling considerations, namely, by particle image velocimetry measurements to observe the evolution of length and velocity scales in the shear layer during transition, and by comparison to direct numerical simulations to illuminate the properties of the front-face boundary layer. The nonlinear dependence of the shear layer instability frequency is sustained by the influence of 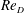 $Re_{D}$ on the thickness of the laminar front-face boundary layer. In corroboration with the original scaling argument for the circular cylinder, the length scale of the shear layer was the only source of nonlinearity in the frequency ratio scaling, within the range of Reynolds numbers reported. The frequency ratio scaling may therefore be understood by the influence of
$Re_{D}$ on the thickness of the laminar front-face boundary layer. In corroboration with the original scaling argument for the circular cylinder, the length scale of the shear layer was the only source of nonlinearity in the frequency ratio scaling, within the range of Reynolds numbers reported. The frequency ratio scaling may therefore be understood by the influence of 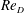 $Re_{D}$ on the appropriate length scale of the shear layer. This length scale was observed to be the momentum thickness evaluated at a transition point, defined where the Kelvin–Helmholtz instability saturates.
$Re_{D}$ on the appropriate length scale of the shear layer. This length scale was observed to be the momentum thickness evaluated at a transition point, defined where the Kelvin–Helmholtz instability saturates.




