Hostname: page-component-77c89778f8-vsgnj Total loading time: 0 Render date: 2024-07-18T20:42:27.889Z Has data issue: false hasContentIssue false
  • English
  • Français

Robust identification of dynamically distinct regions in stratified turbulence

Published online by Cambridge University Press:  18 October 2016

G. D. Portwood ,
S. M. de Bruyn Kops Open the ORCID record for S. M. de Bruyn Kops [Opens in a new window] ,
J. R. Taylor ,
H. Salehipour Open the ORCID record for H. Salehipour [Opens in a new window]  and
C. P. Caulfield
G. D. Portwood*
Affiliation:
Department of Mechanical and Industrial Engineering, University of Massachusetts, Amherst, MA 01003, USA
S. M. de Bruyn Kops
Affiliation:
Department of Mechanical and Industrial Engineering, University of Massachusetts, Amherst, MA 01003, USA
J. R. Taylor
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Cambridge CB3 0WA, UK
H. Salehipour
Affiliation:
Department of Physics, University of Toronto, Toronto, ON, M5S 1A7, Canada
C. P. Caulfield
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Cambridge CB3 0WA, UK BP Institute for Multiphase Flow, University of Cambridge, Cambridge CB3 0EZ, UK
*
†Email address for correspondence: gportwoo@umass.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a new robust method for identifying three dynamically distinct regions in a stratified turbulent flow, which we characterise as quiescent flow, intermittent layers and turbulent patches. The method uses the cumulative filtered distribution function of the local density gradient to identify each region. 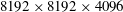We apply it to data from direct numerical simulations of homogeneous stratified turbulence, with unity Prandtl number, resolved on up to $8192\times 8192\times 4096$ grid points. In addition to classifying regions consistently with contour plots of potential enstrophy, our method identifies quiescent regions as regions where 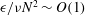$\unicode[STIX]{x1D716}/\unicode[STIX]{x1D708}N^{2}\sim O(1)$, layers as regions where 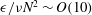$\unicode[STIX]{x1D716}/\unicode[STIX]{x1D708}N^{2}\sim O(10)$ and patches as regions where 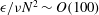$\unicode[STIX]{x1D716}/\unicode[STIX]{x1D708}N^{2}\sim O(100)$. Here, $\unicode[STIX]{x1D716}$ is the dissipation rate of turbulence kinetic energy, $\unicode[STIX]{x1D708}$ is the kinematic viscosity and 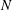$N$ is the (overall) buoyancy frequency. By far the highest local dissipation and mixing rates, and the majority of dissipation and mixing, occur in patch regions, even when patch regions occupy only 5 % of the flow volume. We conjecture that treating stratified turbulence as an instantaneous assemblage of these different regions in varying proportions may explain some of the apparently highly scattered flow dynamics and statistics previously reported in the literature.

JFM classification

Turbulent Flows: Stratified turbulence Turbulent Flows: Turbulent Flows
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 807 , 25 November 2016 , R2
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Almalkie, S. & de Bruyn Kops, S. M. 2012a Energy dissipation rate surrogates in incompressible Navier–Stokes turbulence. J. Fluid Mech. 697, 204–236.Google Scholar
Almalkie, S. & de Bruyn Kops, S. M. 2012b Kinetic energy dynamics in forced, homogeneous, and axisymmetric stably stratified turbulence. J. Turbul. 13 (29), 1–29.Google Scholar
Antonia, R. A. 1981 Conditional sampling in turbulence measurement. Annu. Rev. Fluid Mech. 13 (1), 131–156.CrossRefGoogle Scholar
Bartello, P. & Tobias, S. M. 2013 Sensitivity of stratified turbulence to buoyancy Reynolds number. J. Fluid Mech. 725, 1–22.CrossRefGoogle Scholar
Billant, P. & Chomaz, J.-M. 2001 Self-similarity of strongly stratified inviscid flows. Phys. Fluids 13, 1645–1651.Google Scholar
Brethouwer, G., Billant, P., Lindborg, E. & Chomaz, J.-M. 2007 Scaling analysis and simulation of strongly stratified turbulent flows. J. Fluid Mech. 585, 343–368.Google Scholar
de Bruyn Kops, S. M. 2015 Classical turbulence scaling and intermittency in stably stratified Boussinesq turbulence. J. Fluid Mech. 775, 436–463.CrossRefGoogle Scholar
Dimotakis, P. E. 2005 Turbulent mixing. Annu. Rev. Fluid Mech. 37, 329–356.Google Scholar
Falder, M., White, N. J. & Caulfield, C. P. 2016 Seismic imaging of rapid onset of stratified turbulence in the south Atlantic Ocean. J. Phys. Oceanogr. 46 (4), 1023–1044.CrossRefGoogle Scholar
Gargett, A., Osborn, T. & Nasmyth, P. 1984 Local isotropy and the decay of turbulence in a stratified fluid. J. Fluid Mech. 144, 231–280.Google Scholar
Gibson, C. H. 1980 Fossil turbulence, salinity, and vorticity turbulence in the ocean. In Marine Turbulence (ed. Nihous, J. C.), pp. 221–257. Elsevier.Google Scholar
Gibson, C. H. 1986 Internal waves, fossil turbulence, and composite ocean microstructure spectra. J. Fluid Mech. 168, 89–117.Google Scholar
Hebert, D. A. & de Bruyn Kops, S. M. 2006a Predicting turbulence in flows with strong stable stratification. Phys. Fluids 18 (6), 1–10.Google Scholar
Hebert, D. A. & de Bruyn Kops, S. M. 2006b Relationship between vertical shear rate and kinetic energy dissipation rate in stably stratified flows. Geophys. Res. Lett. 33, L06602.CrossRefGoogle Scholar
Hedley, T. B. & Keffer, J. F. 1974 Turbulent/non-turbulent decisions in an intermittent flow. J. Fluid Mech. 64 (04), 625–644.Google Scholar
Itsweire, E. C., Koseff, J. R., Briggs, D. A. & Ferziger, J. H. 1993 Turbulence in stratified shear flows: implications for interpreting shear-induced mixing in the ocean. J. Phys. Oceanogr. 23, 1508–1522.2.0.CO;2>CrossRefGoogle Scholar
Jackson, P. R. & Rehmann, C. R. 2014 Experiments on differential scalar mixing in turbulence in a sheared, stratified flow. J. Phys. Oceanogr. 44 (10), 2661–2680.Google Scholar
Kimura, Y. & Herring, J. R. 2012 Energy spectra of stably stratified turbulence. J. Fluid Mech. 698, 19–50.Google Scholar
Kuo, A. Y. & Corrsin, S. 1971 Experiments on internal intermittency and fine-structure distribution function in fully turbulent fluid. J. Fluid Mech. 50, 285–320.Google Scholar
Lilly, D. K. 1983 Stratified turbulence and the mesoscale variability of the atmosphere. J. Atmos. Sci. 40, 749–761.Google Scholar
Lin, J.-T. & Pao, Y.-H. 1979 Wakes in stratified fluids: a review. Annu. Rev. Fluid Mech. 11, 317–338.Google Scholar
Lindborg, E. 2006 The energy cascade in a strongly stratified fluid. J. Fluid Mech. 550, 207–242.Google Scholar
Maffioli, A., Brethouwer, G. & Lindborg, E. 2016 Mixing efficiency in stratified turbulence. J. Fluid Mech. 794, R3.CrossRefGoogle Scholar
Maffioli, A. & Davidson, P. A. 2016 Dynamics of stratified turbulence decaying from a high buoyancy Reynolds. J. Fluid Mech. 786, 210–233.CrossRefGoogle Scholar
Nolan, K. P. & Zaki, T. A. 2013 Conditional sampling of transitional boundary layers in pressure gradients. J. Fluid Mech. 728, 306–339.Google Scholar
Praud, O., Fincham, A. M. & Sommeria, J. 2005 Decaying grid turbulence in a strongly stratified fluid. J. Fluid Mech. 522, 1–33.CrossRefGoogle Scholar
Rao, K. J. & de Bruyn Kops, S. M. 2011 A mathematical framework for forcing turbulence applied to horizontally homogeneous stratified flow. Phys. Fluids 23, 065110.Google Scholar
Riley, J. J. & de Bruyn Kops, S. M. 2003 Dynamics of turbulence strongly influenced by buoyancy. Phys. Fluids 15 (7), 2047–2059.Google Scholar
Riley, J. J. & Lindborg, E. 2008 Stratified turbulence: a possible interpretation of some geophysical turbulence measurements. J. Atmos. Sci. 65 (7), 2416–2424.Google Scholar
Rohr, J. J., Itsweire, E. C., Helland, K. N. & Atta, C. W. V. 1988 Growth and decay of turbulence in a stably stratified shear flow. J. Fluid Mech. 195, 77–111.Google Scholar
Salehipour, H. & Peltier, W. 2015 Diapycnal diffusivity, turbulent Prandtl number and mixing efficiency in Boussinesq stratified turbulence. J. Fluid Mech. 775, 464–500.Google Scholar
Salehipour, H., Peltier, W. R., Whalen, C. B. & Mackinnon, J. A. 2016 A new characterization of the turbulent diapycnal diffusivities of mass and momentum in the ocean. Geophys. Res. Lett. 43 (7), 3370–3379.CrossRefGoogle Scholar
Shih, L. H., Koseff, J. R., Ivey, G. N. & Ferziger, J. H. 2005 Parameterization of turbulent fluxes and scales using homogeneous sheared stably stratified turbulence simulations. J. Fluid Mech. 525, 193–214.Google Scholar
Sreenivasan, K. R. 1998 An update on the energy dissipation rate in isotropic turbulence. Phys. Fluids 10 (2), 528–529.Google Scholar
Watanabe, T., Riley, J. J., de Bruyn Kops, S. M., Diamessis, P. J. & Zhou, Q. 2016 Turbulent/non-turbulent interfaces in wakes in stably stratified fluids. J. Fluid Mech. 797, R1.Google Scholar