Article contents
Regimes of two-dimensionality of decaying shallow axisymmetric swirl flows with background rotation
Published online by Cambridge University Press: 01 December 2011
Abstract
Both background rotation and small depths are said to enforce the two-dimensionality of flows. In the current paper, we describe a systematic study of the two-dimensionality of a shallow monopolar vortex subjected to background rotation. Using a perturbation analysis of the Navier–Stokes equations for small aspect ratio 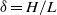 (with
(with 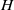 the fluid depth and
the fluid depth and 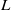 a typical radial length scale of the vortex), we found nine different regimes in the parameter space where the flow is governed to lowest order by different sets of equations. From the properties of these sets of equations, it was determined that the flow can be considered as quasi-two-dimensional in only five of the nine regimes. The scaling of the velocity components as given by these sets of equations was compared with results from numerical simulations to find the actual boundaries of the different regimes in the parameter space (
a typical radial length scale of the vortex), we found nine different regimes in the parameter space where the flow is governed to lowest order by different sets of equations. From the properties of these sets of equations, it was determined that the flow can be considered as quasi-two-dimensional in only five of the nine regimes. The scaling of the velocity components as given by these sets of equations was compared with results from numerical simulations to find the actual boundaries of the different regimes in the parameter space (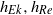 ), where
), where 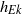 is the Ekman boundary layer thickness and
is the Ekman boundary layer thickness and 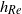 is the equivalent boundary layer thickness for a monopolar vortex without background rotation. Even though background rotation and small depths do promote the two-dimensionality of flows independently, the combination of these two characteristics does not necessarily have that same effect.
is the equivalent boundary layer thickness for a monopolar vortex without background rotation. Even though background rotation and small depths do promote the two-dimensionality of flows independently, the combination of these two characteristics does not necessarily have that same effect.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2011
References
- 8
- Cited by




