Article contents
Quasi-geostrophic approximation of anelastic convection
Published online by Cambridge University Press: 18 June 2014
Abstract
The onset of convection in a rotating cylindrical annulus with parallel ends filled with a compressible fluid is studied in the anelastic approximation. Thermal Rossby waves propagating in the azimuthal direction are found as solutions. The analogy to the case of Boussinesq convection in the presence of conical end surfaces of the annular region is emphasised. As in the latter case, the results can be applied as an approximation for the description of the onset of anelastic convection in rotating spherical fluid shells. Reasonable agreement with three-dimensional numerical results published by Jones, Kuzanyan & Mitchell (J. Fluid Mech., vol. 634, 2009, pp. 291–319) for the latter problem is found. As in those results, the location of the onset of convection shifts outwards from the tangent cylinder with increasing number 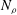 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}N_{\rho }$ of density scale heights until it reaches the equatorial boundary. A new result is that at a much higher number
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}N_{\rho }$ of density scale heights until it reaches the equatorial boundary. A new result is that at a much higher number 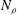 $N_{\rho }$ the onset location returns to the interior of the fluid shell.
$N_{\rho }$ the onset location returns to the interior of the fluid shell.
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 6
- Cited by




