Article contents
Progression of heavy plates from stable falling to tumbling flight
Published online by Cambridge University Press: 11 July 2018
Abstract
This study examines the transition of stable falling to tumbling flight for freely falling heavy plates in a two-dimensional viscous fluid, solved via direct numerical simulation with the immersed boundary method. The simulations are performed at a range of Reynolds number (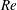 $Re$) of up to 500 and a dimensionless moment of inertia (
$Re$) of up to 500 and a dimensionless moment of inertia (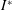 $I^{\ast }$) up to 10. It is found that a plate may settle to stable falling or develop into tumbling descent depending on the initial angle of release
$I^{\ast }$) up to 10. It is found that a plate may settle to stable falling or develop into tumbling descent depending on the initial angle of release 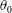 $\unicode[STIX]{x1D703}_{0}$. The characteristics and performance that distinguish two flight states are investigated. This bistability is analysed with phase portraits and the region mapped across the regime of
$\unicode[STIX]{x1D703}_{0}$. The characteristics and performance that distinguish two flight states are investigated. This bistability is analysed with phase portraits and the region mapped across the regime of 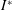 $I^{\ast }$ and
$I^{\ast }$ and 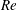 $Re$ at a specific thickness ratio. In determining the flight state, the respective critical
$Re$ at a specific thickness ratio. In determining the flight state, the respective critical 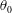 $\unicode[STIX]{x1D703}_{0}$ is found to follow a power law through
$\unicode[STIX]{x1D703}_{0}$ is found to follow a power law through 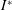 $I^{\ast }$ and
$I^{\ast }$ and 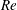 $Re$. It is suggested that the changing slope of the lift curve that the plate undergoes sets the two flight states apart. Flow fields also reveal that the recirculation behind the plate is confined by the vortex structures and provides an additional rotation to the plate. An experiment is performed suggesting that bistability also occurs at Re
$Re$. It is suggested that the changing slope of the lift curve that the plate undergoes sets the two flight states apart. Flow fields also reveal that the recirculation behind the plate is confined by the vortex structures and provides an additional rotation to the plate. An experiment is performed suggesting that bistability also occurs at Re 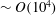 ${\sim}O(10^{4})$. Other shapes are also simulated and the different bistable effects are discussed.
${\sim}O(10^{4})$. Other shapes are also simulated and the different bistable effects are discussed.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 15
- Cited by





