Hostname: page-component-76fb5796d-qxdb6 Total loading time: 0 Render date: 2024-04-27T00:56:55.828Z Has data issue: false hasContentIssue false
  • English
  • Français

Post-shock turbulence recovery in oblique-shock/turbulent boundary layer interaction flows

Published online by Cambridge University Press:  24 April 2023

Ming Yu Open the ORCID record for Ming Yu [Opens in a new window] ,
SiWei Dong Open the ORCID record for SiWei Dong [Opens in a new window] ,
PengXin Liu ,
ZhiGong Tang ,
XianXu Yuan Open the ORCID record for XianXu Yuan [Opens in a new window]  and
ChunXiao Xu Open the ORCID record for ChunXiao Xu [Opens in a new window]
Ming Yu
Affiliation:
State Key Laboratory of Aerodynamics, Mianyang 621000, PR China Key Laboratory of Applied Mechanics, Ministry of Education, Institute of Fluid Mechanics, Department of Engineering Mechanics, Tsinghua University, Beijing 100084, PR China
SiWei Dong
Affiliation:
State Key Laboratory of Aerodynamics, Mianyang 621000, PR China
PengXin Liu
Affiliation:
State Key Laboratory of Aerodynamics, Mianyang 621000, PR China
ZhiGong Tang
Affiliation:
State Key Laboratory of Aerodynamics, Mianyang 621000, PR China
XianXu Yuan*
Affiliation:
State Key Laboratory of Aerodynamics, Mianyang 621000, PR China
ChunXiao Xu
Affiliation:
Key Laboratory of Applied Mechanics, Ministry of Education, Institute of Fluid Mechanics, Department of Engineering Mechanics, Tsinghua University, Beijing 100084, PR China
*
†Email addresses for correspondence: yuanxianxu@cardc.cn, xucx@tsinghua.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

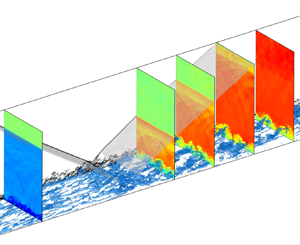
The oblique shock impinging on the supersonic turbulent boundary layer leads to a mixing layer and the emergence of large-scale coherent structures within the interaction zone which leave significant velocity defect and turbulence amplification downstream. In the present study, we investigate the turbulence recovery in the post-shock region by exploiting direct numerical simulation data of the oblique-shock/turbulent boundary layer interaction flow at the incoming Mach number of $2.28$ and the shock angle of $33.2^\circ$, with special attention paid to the contribution of the mixing layer and large-scale structures to flow dynamics. For that purpose, we propose to split the mean velocity, Reynolds stresses and spanwise spectra into a canonical portion that is constructed according to the statistics of canonical turbulent boundary layers, and a mixing-layer-induced portion. We found that the hidden mixing layer grows with the boundary layer thickness and that the induced mean shear and Reynolds stresses decay at different rates. The mean velocity recovers to the canonical profiles at a distance of 13 boundary layer thicknesses downstream where the mixing-layer-induced mean shear ceases to have strong impacts. The recovery of Reynolds stresses requires 10 boundary layer thicknesses in the near-wall region but a much longer streamwise extent in the outer region due to the slow decay of large-scale motions. These large-scale motions superpose on the near-wall turbulence, intensifying the turbulent fluctuations, yet having a trivial impact on the skin friction, for the contribution of the mixing-layer-induced mean shear and Reynolds shear stress are balanced by the advection term. We further establish a simple physical model capable of approximately predicting the streamwise evolution of mixing-layer-induced mean shear and turbulent kinetic energy. This model suggests that the complete recovery of turbulence in the outer region requires a streamwise extent of approximately 50 boundary layer thicknesses.

JFM classification

Compressible Flows: Compressible boundary layers Compressible Flows: Shock waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 961 , 25 April 2023 , A26
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, M.C. & Gaitonde, D.V. 2020 Dynamics of strong swept-shock/turbulent-boundary-layer interactions. J. Fluid Mech. 896, A29.CrossRefGoogle Scholar
Andreopoulos, Y., Agui, J. & Briassulis, G. 2000 Shock wave–turbulence interactions. Annu. Rev. Fluid Mech. 32 (1), 309–345.CrossRefGoogle Scholar
Babinsky, H. & Harvey, J. 2011 Shock Wave-boundary-layer Interactions, vol. 32. Cambridge University Press.CrossRefGoogle Scholar
Baidya, R., Scharnowski, S., Bross, M. & Kähler, C. 2020 Interactions between a shock and turbulent features in a Mach 2 compressible boundary layer. J. Fluid Mech. 893, A15.Google Scholar
Bell, J. & Mehta, R. 1990 Development of a two-stream mixing layer from tripped and untripped boundary layers. AIAA J. 28 (12), 2034–2042.Google Scholar
Bernardini, M., Asproulias, I., Larsson, J., Pirozzoli, S. & Grasso, F. 2016 Heat transfer and wall temperature effects in shock wave turbulent boundary layer interactions. Phys. Rev. Fluids 1 (8), 084403.CrossRefGoogle Scholar
Bernardini, M., Modesti, D., Salvadore, F. & Pirozzoli, S. 2021 STREAmS: a high-fidelity accelerated solver for direct numerical simulation of compressible turbulent flows. Comput. Phys. Commun. 263, 107906.CrossRefGoogle Scholar
Bernardini, M., Pirozzoli, S. & Grasso, F. 2011 The wall pressure signature of transonic shock/boundary layer interaction. J. Fluid Mech. 671, 288–312.CrossRefGoogle Scholar
Chambres, O., Barre, S. & Bonnet, J. 1998 Detailed turbulence characteristics of a highly compressible supersonic turbulent plane mixing layer. J. Fluid Mech. (submitted).Google Scholar
Champagne, F., Pao, Y. & Wygnanski, I. 1976 On the two-dimensional mixing region. J. Fluid Mech. 74 (2), 209–250.CrossRefGoogle Scholar
Chandrsuda, C. & Bradshaw, P. 1981 Turbulence structure of a reattaching mixing layer. J. Fluid Mech. 110, 171–194.CrossRefGoogle Scholar
Chen, X. & Sreenivasan, K. 2021 Reynolds number scaling of the peak turbulence intensity in wall flows. J. Fluid Mech. 908, R3.CrossRefGoogle Scholar
Cheng, C., Li, W., Lozano-Duran, A. & Liu, H. 2020 Uncovering Townsend's wall-attached eddies in low-Reynolds-number wall turbulence. J. Fluid Mech. 889, A29.CrossRefGoogle Scholar
Clemens, N. & Narayanaswamy, V. 2014 Low-frequency unsteadiness of shock wave/turbulent boundary layer interactions. Annu. Rev. Fluid Mech. 46, 469–492.CrossRefGoogle Scholar
Delery, J. 1985 Shock wave/turbulent boundary layer interaction and its control. Prog. Aerosp. Sci. 22 (4), 209–280.CrossRefGoogle Scholar
Ding, L. & Smits, A. 2021 Relaxation of turbulent pipe flow downstream of a square bar roughness element. J. Fluid Mech. 922, A34.CrossRefGoogle Scholar
Dolling, D. 2001 Fifty years of shock-wave/boundary-layer interaction research: what next? AIAA J. 39 (8), 1517–1531.CrossRefGoogle Scholar
Ducros, F., Ferrand, V., Nicoud, F., Weber, C., Darracq, D., Gacherieu, C. & Poinsot, T. 1999 Large-eddy simulation of the shock/turbulence interaction. J. Comput. Phys. 152 (2), 517–549.CrossRefGoogle Scholar
Dupont, P., Haddad, C. & Debieve, J. 2006 Space and time organization in a shock-induced separated boundary layer. J. Fluid Mech. 559, 255–277.Google Scholar
Dupont, P., Piponniau, S. & Dussauge, J. 2019 Compressible mixing layer in shock-induced separation. J. Fluid Mech. 863, 620–643.CrossRefGoogle Scholar
Dupont, P., Piponniau, S., Sidorenko, A. & Debieve, J. 2008 Investigation by particle image velocimetry measurements of oblique shock reflection with separation. AIAA J. 46 (6), 1365–1370.CrossRefGoogle Scholar
Fan, Y., Li, W. & Pirozzoli, S. 2019 Decomposition of the mean friction drag in zero-pressure-gradient turbulent boundary layers. Phys. Fluids 31 (8), 086105.Google Scholar
Fang, J., Zheltovodov, A., Yao, Y., Moulinec, C. & Emerson, D. 2020 On the turbulence amplification in shock-wave/turbulent boundary layer interaction. J. Fluid Mech. 897, A32.CrossRefGoogle Scholar
Foysi, H., Sarkar, S. & Friedrich, R. 2004 Compressibility effects and turbulence scalings in supersonic channel flow. J. Fluid Mech. 509, 207–216.CrossRefGoogle Scholar
Gaitonde, D. 2015 Progress in shock wave/boundary layer interactions. Prog. Aerosp. Sci. 72, 80–99.Google Scholar
Ganapathisubramani, B., Clemens, N. & Dolling, D. 2007 Effects of upstream boundary layer on the unsteadiness of shock-induced separation. J. Fluid Mech. 585, 369–394.CrossRefGoogle Scholar
Gatski, T. & Bonnet, J. 2013 Compressibility, Turbulence and High Speed Flow. Academic Press.Google Scholar
Helm, C., Martín, M. & Williams, O. 2021 Characterization of the shear layer in separated shock/turbulent boundary layer interactions. J. Fluid Mech. 912, A7.CrossRefGoogle Scholar
Hu, R. & Zheng, X. 2018 Energy contributions by inner and outer motions in turbulent channel flows. Phys. Rev. Fluids 3 (8), 084607.CrossRefGoogle Scholar
Humble, R., Scarano, F. & van Oudheusden, B. 2009 Unsteady aspects of an incident shock wave/turbulent boundary layer interaction. J. Fluid Mech. 635, 47–74.Google Scholar
Hwang, Y. 2013 Near-wall turbulent fluctuations in the absence of wide outer motions. J. Fluid Mech. 723, 264–288.Google Scholar
Hwang, Y. 2015 Statistical structure of self-sustaining attached eddies in turbulent channel flow. J. Fluid Mech. 767, 254–289.CrossRefGoogle Scholar
Jammalamadaka, A., Li, Z. & Jaberi, F. 2014 Numerical investigations of shock wave interactions with a supersonic turbulent boundary layer. Phys. Fluids 26 (5), 87–108.CrossRefGoogle Scholar
Jiang, G. & Shu, C. 1996 Efficient implementation of weighted ENO schemes. J. Comput. Phys. 126 (1), 202–228.CrossRefGoogle Scholar
Khlifi, H. & Lili, T. 2016 On the compressibility effects in mixing layers. Therm. Sci. 20 (5), 1473–1484.CrossRefGoogle Scholar
Klein, M., Sadiki, A. & Janicka, J. 2003 A digital filter based generation of inflow data for spatially developing direct numerical or large eddy simulations. J. Comput. Phys. 186 (2), 652–665.CrossRefGoogle Scholar
Kumar, P. & Mahesh, K. 2021 Simple model for mean stress in turbulent boundary layers. Phys. Rev. Fluids 6 (2), 024603.CrossRefGoogle Scholar
Li, D., Komperda, J., Peyvan, A., Ghiasi, Z. & Mashayek, F. 2022 Assessment of turbulence models using DNS data of compressible plane free shear layer flow. J. Fluid Mech. 931, A10.CrossRefGoogle Scholar
Li, X., Fu, D., Ma, Y. & Liang, X. 2010 Direct numerical simulation of shock/turbulent boundary layer interaction in a supersonic compression ramp. Sci. China Phys. Mech. 53 (9), 1651–1658.CrossRefGoogle Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010 High Reynolds number effects in wall turbulence. Intl J. Heat Fluid Flow 31 (3), 418–428.CrossRefGoogle Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2011 A predictive inner–outer model for streamwise turbulence statistics in wall-bounded flows. J. Fluid Mech. 681, 537–566.CrossRefGoogle Scholar
Morgan, B., Duraisamy, K., Nguyen, N., Kawai, S. & Lele, S.K. 2013 Flow physics and RANS modelling of oblique shock/turbulent boundary layer interaction. J. Fluid Mech. 729, 231–284.CrossRefGoogle Scholar
Musker, A. 1979 Explicit expression for the smooth wall velocity distribution in a turbulent boundary layer. AIAA J. 17 (6), 655–657.CrossRefGoogle Scholar
Pantano, C. & Sarkar, S. 2002 A study of compressibility effects in the high-speed turbulent shear layer using direct simulation. J. Fluid Mech. 451, 329–371.CrossRefGoogle Scholar
Patel, R. 1973 An experimental study of a plane mixing layer. AIAA J. 11 (1), 67–71.Google Scholar
Piponniau, S., Dussauge, J., Debieve, J. & Dupont, P. 2009 A simple model for low-frequency unsteadiness in shock-induced separation. J. Fluid Mech. 629, 87–108.CrossRefGoogle Scholar
Pirozzoli, S. 2010 Generalized conservative approximations of split convective derivative operators. J. Comput. Phys. 229 (19), 7180–7190.CrossRefGoogle Scholar
Pirozzoli, S. & Bernardini, M. 2011 a Direct numerical simulation database for impinging shock wave/turbulent boundary-layer interaction. AIAA J. 49 (6), 1307–1312.CrossRefGoogle Scholar
Pirozzoli, S. & Bernardini, M. 2011 b Turbulence in supersonic boundary layers at moderate Reynolds number. J. Fluid Mech. 688, 120–168.CrossRefGoogle Scholar
Pirozzoli, S., Bernardini, M. & Grasso, F. 2010 Direct numerical simulation of transonic shock/boundary layer interaction under conditions of incipient separation. J. Fluid Mech. 657, 361–393.CrossRefGoogle Scholar
Pirozzoli, S. & Colonius, T. 2013 Generalized characteristic relaxation boundary conditions for unsteady compressible flow simulations. J. Comput. Phys. 248, 109–126.CrossRefGoogle Scholar
Pirozzoli, S. & Grasso, F. 2006 Direct numerical simulation of impinging shock wave/turbulent boundary layer interaction at $M= 2.25$. Phys. Fluids 18 (6), 065113.CrossRefGoogle Scholar
Pope, S. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Priebe, S. & Martín, M. 2012 Low-frequency unsteadiness in shock wave-turbulent boundary layer interaction. J. Fluid Mech. 699, 1–49.CrossRefGoogle Scholar
Renard, N. & Deck, S. 2016 A theoretical decomposition of mean skin friction generation into physical phenomena across the boundary layer. J. Fluid Mech. 790, 339–367.CrossRefGoogle Scholar
Robinson, S. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23 (1), 601–639.Google Scholar
Samimy, M., Reeder, M. & Elliott, G. 1992 Compressibility effects on large structures in free shear flows. Phys. Fluids 4 (6), 1251–1258.CrossRefGoogle Scholar
Selig, M., Andreopoulos, J., Muck, K., Dussauge, J. & Smits, A. 1989 Turbulence structure in a shock wave/turbulent boundary-layer interaction. AIAA J. 27 (7), 862–869.CrossRefGoogle Scholar
Smits, A. 2020 Some observations on Reynolds number scaling in wall-bounded flows. Phys. Rev. Fluids 5 (11), 110514.Google Scholar
Smits, A. & Dussauge, J. 2006 Turbulent Shear Layers in Supersonic Flow. Springer Science & Business Media.Google Scholar
Smits, A. & Hultmark, M. 2021 Reynolds stress scaling in the near-wall region. arXiv:2103.07341.Google Scholar
Smits, A., Hultmark, M., Lee, M., Pirozzoli, S. & Wu, X. 2021 Reynolds stress scaling in the near-wall region of wall-bounded flows. arXiv:2106.05053.CrossRefGoogle Scholar
Smits, A. & Muck, K. 1987 Experimental study of three shock wave/turbulent boundary layer interactions. J. Fluid Mech. 182, 291–314.CrossRefGoogle Scholar
Tong, F., Yu, C., Tang, Z. & Li, X. 2017 Numerical studies of shock wave interactions with a supersonic turbulent boundary layer in compression corner: turning angle effects. Comput. Fluids 149, 56–69.Google Scholar
Townsend, A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Volpiani, P., Bernardini, M. & Larsson, J. 2018 Effects of a nonadiabatic wall on supersonic shock/boundary-layer interactions. Phys. Rev. Fluids 3 (8), 083401.CrossRefGoogle Scholar
Volpiani, P., Bernardini, M. & Larsson, J. 2020 Effects of a nonadiabatic wall on hypersonic shock/boundary-layer interactions. Phys. Rev. Fluids 5 (1), 014602.CrossRefGoogle Scholar
Wang, H., Wang, S. & He, G. 2018 The spanwise spectra in wall-bounded turbulence. Acta Mechanica Sin. 34 (3), 452–461.CrossRefGoogle Scholar
Wang, L., Hu, R. & Zheng, X. 2021 A scaling improved inner–outer decomposition of near-wall turbulent motions. Phys. Fluids 33 (4), 045120.CrossRefGoogle Scholar
Wray, A. 1990 Minimal storage time advancement schemes for spectral methods. Rep. No. MS 202. NASA Ames Research Center.Google Scholar
Wu, M. & Martin, M. 2007 Direct numerical simulation of supersonic turbulent boundary layer over a compression ramp. AIAA J. 45 (4), 879–889.CrossRefGoogle Scholar
Wu, M. & Martin, M. 2008 Analysis of shock motion in shockwave and turbulent boundary layer interaction using direct numerical simulation data. J. Fluid Mech. 594, 71–83.Google Scholar
Yin, G., Huang, W. & Xu, C. 2017 On near-wall turbulence in minimal flow units. Intl J. Heat Fluid Flow 65, 192–199.CrossRefGoogle Scholar
Yu, M., Zhao, M.X., Tang, Z.G., Yuan, X.X. & Xu, C.X. 2022 A spectral inspection for turbulence amplification in oblique shock wave/turbulent boundary layer interaction. J. Fluid Mech. 951, A2.CrossRefGoogle Scholar
Zhang, Y., Bi, W., Hussain, F. & She, Z. 2014 A generalized Reynolds analogy for compressible wall-bounded turbulent flows. J. Fluid Mech. 739, 392–420.CrossRefGoogle Scholar
Zheltovodov, A., Lebiga, V. & Yakovlev, V. 1989 Measurement of turbulence characteristics in compressible boundary layers near separation zones. J. Appl. Mech. Tech. Phys. 30 (3), 442–447.CrossRefGoogle Scholar
Zhuang, Y., Tan, H., Li, X., Guo, Y. & Sheng, F. 2018 Evolution of coherent vortical structures in a shock wave/turbulent boundary-layer interaction flow. Phys. Fluids 30 (11), 111702.CrossRefGoogle Scholar
Zuo, F., Memmolo, A., Huang, G. & Pirozzoli, S. 2019 Direct numerical simulation of conical shock wave–turbulent boundary layer interaction. J. Fluid Mech. 877, 167–195.Google Scholar