Hostname: page-component-77c89778f8-9q27g Total loading time: 0 Render date: 2024-07-16T23:18:12.490Z Has data issue: false hasContentIssue false
  • English
  • Français

Parametric subharmonic instability in a narrow-band wave spectrum

Published online by Cambridge University Press:  18 February 2019

Yohei Onuki Open the ORCID record for Yohei Onuki [Opens in a new window]  and
Toshiyuki Hibiya
Yohei Onuki*
Affiliation:
Research Institute for Applied Mechanics, Kyushu University, Kasuga, Fukuoka 816-8580, Japan
Toshiyuki Hibiya
Affiliation:
Department of Earth and Planetary Science, Graduate School of Science, The University of Tokyo, Tokyo 113-0033, Japan
*
†Email address for correspondence: onuki@riam.kyushu-u.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

Parametric subharmonic instability arising in a narrow-band wave spectrum is investigated. Using a statistical equation that describes weakly nonlinear interactions in a random wave field, we perform analytical and numerical stability analyses for a modulating wave train. The analytically obtained growth rate 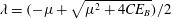$\unicode[STIX]{x1D706}=(-\unicode[STIX]{x1D707}+\sqrt{\unicode[STIX]{x1D707}^{2}+4CE_{B}})/2$ agrees favourably with the results from direct numerical experiments, where 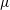$\unicode[STIX]{x1D707}$ is the half-value width of the background wave frequency spectrum, 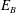$E_{B}$ is the background wave energy density, and 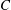$C$ is a constant. This expression has two asymptotic limits: 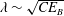$\unicode[STIX]{x1D706}\sim \sqrt{CE_{B}}$ for 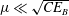$\unicode[STIX]{x1D707}\ll \sqrt{CE_{B}}$ and $\unicode[STIX]{x1D706}\sim CE_{B}/\unicode[STIX]{x1D707}$ for 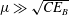$\unicode[STIX]{x1D707}\gg \sqrt{CE_{B}}$. In the terms of weak turbulence, these two growth rates correspond to the ones occurring in the dynamic and kinetic time scales. In this way, our formulation successfully unifies the two conventional types of parametric subharmonic instability and offers a new criterion to determine the applicability of the classical kinetic equation in three-wave systems.

JFM classification

Geophysical and Geological Flows: Internal waves Instability: Parametric instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 865 , 25 April 2019 , pp. 247 - 280
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alber, I. E. 1978 The effects of randomness on the stability of two-dimensional surface wavetrains. Proc. R. Soc. Lond. A 363 (1715), 525–546.10.1098/rspa.1978.0181Google Scholar
Alford, M. H. & Zhao, Z. 2007 Global patterns of low-mode internal-wave propagation. Part I: Energy and energy flux. J. Phys. Oceanogr. 37 (7), 1829–1848.10.1175/JPO3085.1Google Scholar
Annenkov, S. Y. & Shrira, V. I. 2006 Role of non-resonant interactions in the evolution of nonlinear random water wave fields. J. Fluid Mech. 561, 181–207.10.1017/S0022112006000632Google Scholar
Annenkov, S. Y. & Shrira, V. I. 2015 Modelling the impact of squall on wind waves with the generalized kinetic equation. J. Phys. Oceanogr. 45 (3), 807–812.10.1175/JPO-D-14-0182.1Google Scholar
Annenkov, S. Y. & Shrira, V. I. 2018 Spectral evolution of weakly nonlinear random waves: kinetic description versus direct numerical simulations. J. Fluid Mech. 844, 766–795.10.1017/jfm.2018.185Google Scholar
Bender, C. M. & Orszag, S. A. 1999 Advanced Mathematical Methods for Scientists and Engineers I: Asymptotic Methods and Perturbation Theory. Springer.10.1007/978-1-4757-3069-2Google Scholar
Benjamin, T. B. & Feir, J. E. 1967 The disintegration of wave trains on deep water. Part 1. Theory. J. Fluid Mech. 27, 417–430.10.1017/S002211206700045XGoogle Scholar
Bourget, B., Scolan, H., Dauxois, T., Bars, M. L., Odier, P. & Joubaud, S. 2014 Finite-size effects in parametric subharmonic instability. J. Fluid Mech. 759, 739–750.10.1017/jfm.2014.550Google Scholar
Chalamalla, V. K. & Sarkar, S. 2016 PSI in the case of internal wave beam reflection at a uniform slope. J. Fluid Mech. 789, 347–367.10.1017/jfm.2015.608Google Scholar
Chen, L.-Y., Goldenfeld, N. & Oono, Y. 1996 Renormalization group and singular perturbations: multiple scales, boundary layers and reductive perturbation theory. Phys. Rev. E 54, 376–394.10.1103/PhysRevE.54.376Google Scholar
Eden, C. & Olbers, D. 2014 An energy compartment model for propagation, nonlinear interaction, and dissipation of internal gravity waves. J. Phys. Oceanogr. 44 (8), 2093–2106.10.1175/JPO-D-13-0224.1Google Scholar
Floris, C. 2012 Stochastic stability of damped Mathieu oscillator parametrically excited by a Gaussian noise. Math. Problems Engng 2012, 1–18.10.1155/2012/375913Google Scholar
Furuichi, N., Hibiya, T. & Niwa, Y. 2005 Bispectral analysis of energy transfer within the two-dimensional oceanic internal wave field. J. Phys. Oceanogr. 35 (11), 2104–2109.10.1175/JPO2816.1Google Scholar
Gerkema, T., Staquet, C. & Bouruet-Aubertot, P. 2006 Decay of semi-diurnal internal-tide beams due to subharmonic resonance. Geophys. Res. Lett. 33 (8), L08604.10.1029/2005GL025105Google Scholar
Hasselmann, K. 1962 On the non-linear energy transfer in a gravity-wave spectrum. Part 1. General theory. J. Fluid Mech. 12, 481–500.10.1017/S0022112062000373Google Scholar
Hasselmann, K. 1966 Feynman diagrams and interaction rules of wave–wave scattering processes. Rev. Geophys. 4 (1), 1–32.10.1029/RG004i001p00001Google Scholar
Hasselmann, K. 1967 A criterion for nonlinear wave stability. J. Fluid Mech. 30 (04), 737–739.10.1017/S0022112067001739Google Scholar
Hazewinkel, J. & Winters, K. B. 2011 PSI of the internal tide on a 𝛽 plane: flux divergence and near-inertial wave propagation. J. Phys. Oceanogr. 41 (9), 1673–1682.10.1175/2011JPO4605.1Google Scholar
Hibiya, T. & Nagasawa, M. 2004 Latitudinal dependence of diapycnal diffusivity in the thermocline estimated using a finescale parameterization. Geophys. Res. Lett. 31 (1), l01301.10.1029/2003GL017998Google Scholar
Hibiya, T., Nagasawa, M. & Niwa, Y. 2002 Nonlinear energy transfer within the oceanic internal wave spectrum at mid and high latitudes. J. Geophys. Res. 107 (C11), 28–1–28–8, 3207.10.1029/2001JC001210Google Scholar
Hibiya, T., Nagasawa, M. & Niwa, Y. 2006 Global mapping of diapycnal diffusivity in the deep ocean based on the results of expendable current profiler (XCP) surveys. Geophys. Res. Lett. 33 (3), l03611.10.1029/2005GL025218Google Scholar
Holloway, G. 1980 Oceanic internal waves are not weak waves. J. Phys. Oceanogr. 10 (6), 906–914.10.1175/1520-0485(1980)010<0906:OIWANW>2.0.CO;22.0.CO;2>Google Scholar
Janssen, P. A. E. M. 2003 Nonlinear four-wave interactions and freak waves. J. Phys. Oceanogr. 33 (4), 863–884.10.1175/1520-0485(2003)33<863:NFIAFW>2.0.CO;22.0.CO;2>Google Scholar
Karimi, H. H. & Akylas, T. R. 2014 Parametric subharmonic instability of internal waves: locally confined beams versus monochromatic wavetrains. J. Fluid Mech. 757, 381–402.10.1017/jfm.2014.509Google Scholar
Karimi, H. H. & Akylas, T. R. 2017 Near-inertial parametric subharmonic instability of internal wave beams. Phys. Rev. Fluids 2 (7), 074801.10.1103/PhysRevFluids.2.074801Google Scholar
Kartashova, E. 2013 Time scales and structures of wave interaction exemplified with water waves. Europhys. Lett. 102 (4), 44005.10.1209/0295-5075/102/44005Google Scholar
Landau, L. D. & Lifshitz, E. M. 1976 Mechanics. Butterworth-Heinemann.Google Scholar
Lvov, Y. & Tabak, E. G. 2004 A Hamiltonian formulation for long internal waves. Physica D 195 (1–2), 106–122.10.1016/j.physd.2004.03.010Google Scholar
Lvov, Y. V. & Yokoyama, N. 2009 Nonlinear wave–wave interactions in stratified flows: direct numerical simulations. Physica D 238 (8), 803–815.10.1016/j.physd.2009.01.016Google Scholar
MacKinnon, J. A. & Winters, K. B. 2005 Subtropical catastrophe: significant loss of low-mode tidal energy at 28. 9° . Geophys. Res. Lett. 32 (15).10.1029/2005GL023376Google Scholar
MacKinnon, J. A., Zhao, Z., Whalen, C. B., Waterhouse, A. F., Trossman, D. S., Sun, O. M., Laurent, L. C. St., Simmons, H. L., Polzin, K., Pinkel, R., Pickering, A., Norton, N. J., Nash, J. D., Musgrave, R., Merchant, L. M., Melet, A. V., Mater, B., Legg, S., Large, W. G., Kunze, E., Klymak, J. M., Jochum, M., Jayne, S. R., Hallberg, R. W., Griffies, S. M., Diggs, S., Danabasoglu, G., Chassignet, E. P., Buijsman, M. C., Bryan, F. O., Briegleb, B. P., Barna, A., Arbic, B. K., Ansong, J. K. & Alford, M. H. 2017 Climate process team on internal wave-driven ocean mixing. Bull. Am. Meteorol. Soc. 98 (11), 2429–2454.10.1175/BAMS-D-16-0030.1Google Scholar
McComas, C. H. 1977 Equilibrium mechanisms within the oceanic internal wave field. J. Phys. Oceanogr. 7 (6), 836–845.10.1175/1520-0485(1977)007<0836:EMWTOI>2.0.CO;22.0.CO;2>Google Scholar
McComas, C. H. & Müller, P. 1981 Time scales of resonant interactions among oceanic internal waves. J. Phys. Oceanogr. 11 (2), 139–147.10.1175/1520-0485(1981)011<0139:TSORIA>2.0.CO;22.0.CO;2>Google Scholar
Medvedev, S. B. & Zeitlin, V. 2007 Turbulence of near-inertial waves in the continuously stratified fluid. Phys. Lett. A 371 (3), 221–227.10.1016/j.physleta.2007.08.014Google Scholar
Müller, P., Holloway, G., Henyey, F. & Pomphrey, N. 1986 Nonlinear interactions among internal gravity waves. Rev. Geophys. 24 (3), 493–536.10.1029/RG024i003p00493Google Scholar
Nazarenko, S. 2011 Wave Turbulence. Springer.10.1007/978-3-642-15942-8Google Scholar
Olbers, D. J. 1983 Models of the oceanic internal wave field. Rev. Geophys. 21 (7), 1567–1606.10.1029/RG021i007p01567Google Scholar
Olbers, D. J. & Pomphrey, N. 1981 Disqualifying two candidates for the energy balance of oceanic internal waves. J. Phys. Oceanogr. 11 (10), 1423–1425.10.1175/1520-0485(1981)011<1423:DTCFTE>2.0.CO;22.0.CO;2>Google Scholar
Onuki, Y. & Hibiya, T. 2018 Decay rates of internal tides estimated by an improved wave–wave interaction analysis. J. Phys. Oceanogr. 48 (11), 2689–2701.10.1175/JPO-D-17-0278.1Google Scholar
Polzin, K. L. & Lvov, Y. V. 2011 Toward regional characterizations of the oceanic internal wavefield. Rev. Geophys. 49 (4), rG4003.10.1029/2010RG000329Google Scholar
Sonmor, L. J. & Klaassen, G. P. 1997 Toward a unified theory of gravity wave stability. J. Atmos. Sci. 54 (22), 2655–2680.10.1175/1520-0469(1997)054<2655:TAUTOG>2.0.CO;22.0.CO;2>Google Scholar
Stiassnie, M., Regev, A. & Agnon, Y. 2008 Recurrent solutions of Alber’s equation for random water-wave fields. J. Fluid Mech. 598, 245–266.10.1017/S0022112007009998Google Scholar
Young, W. R., Tsang, Y.-K. & Balmforth, N. J. 2008 Near-inertial parametric subharmonic instability. J. Fluid Mech. 607, 25–49.10.1017/S0022112008001742Google Scholar
Zakharov, V. E., L’vov, V. S. & Falkovich, G. 1992 Kolmogorov Spectra of Turbulence I – Wave Turbulence. Springer.10.1007/978-3-642-50052-7Google Scholar
Zaron, E. D. & Egbert, G. D. 2014 Time-variable refraction of the internal tide at the Hawaiian Ridge. J. Phys. Oceanogr. 44 (2), 538–557.10.1175/JPO-D-12-0238.1Google Scholar