Hostname: page-component-848d4c4894-75dct Total loading time: 0 Render date: 2024-06-06T14:04:50.127Z Has data issue: false hasContentIssue false
  • English
  • Français

On vortex-sheet evolution beyond singularity formation

Published online by Cambridge University Press:  30 November 2023

D.I. Pullin Open the ORCID record for D.I. Pullin [Opens in a new window]  and
N. Shen Open the ORCID record for N. Shen [Opens in a new window]
D.I. Pullin*
Affiliation:
Graduate Aerospace Laboratories, California Institute of Technology, CA 91125, USA
N. Shen
Affiliation:
The Fluid Dynamics of Disease Transmission Laboratory, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
*
†Email address for correspondence: dpullin@caltech.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

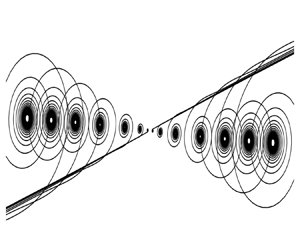
We consider the evolution of a spatially periodic, perturbed vortex sheet for small times after the formation of a curvature singularity at time $t=t_c$ as demonstrated by Moore (Proc. R. Soc. Lond. A, vol. 365, issue 1720, 1979, pp. 105–119). The Moore analysis is extended to provide the small-amplitude, full-sheet structure at $t=t_c$ for a general single-mode initial condition in terms of polylogarithmic functions, from which its asymptotic form near the singular point is determined. This defines an intermediate evolution problem for which the leading-order, and most singular, approximation is solved as a Taylor-series expansion in $\tau = t-t_c$, where coefficients are calculated by repeated differentiation of the defining Birkhoff–Rott (BR) equation. The first few terms are in good agreement with numerical calculation based on the full-sheet solution. The series is summed, providing an analytic continuation which shows sheet rupture at circulation $\varGamma =0^+$, $\tau >0^+$, but with non-physical features owing to the absence of end-tip sheet roll up. This is corrected by constructing an inner solution with $\varGamma < \tau$, as a perturbed similarity form with small parameter $\tau ^{1/2}$. Numerical solutions of both the inner, nonlinear zeroth-order and first-order linear BR equations are obtained whose outer limits match the intermediate solution. The composite solution shows sheet tearing at $\tau =0^+$ into two separate, rolled up algebraic spirals near the central singular point. Branch separation distance scales as $\tau$ with a non-local, $\tau ^{3/2}$ correction. Properties of the intermediate and inner solutions are discussed.

JFM classification

Vortex Flows: Vortex dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 976 , 10 December 2023 , A17
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baker, G.R. & Pham, L. 2006 A comparison of blob methods for vortex sheet roll-up. J. Fluid Mech. 547, 297–316.CrossRefGoogle Scholar
Baker, G.R. & Shelley, M.J. 1990 On the connection between thin vortex layers and vortex sheets. J. Fluid Mech. 215, 161–194.CrossRefGoogle Scholar
Bell, E.T. 1927 Partition polynomials. Ann. Maths 29, 38–46.CrossRefGoogle Scholar
Birkhoff, G. 1962 Helmholtz and Taylor instability. In Proceedings of Symposia in Applied Mathematics (ed. G. Birkhoff, R.E. Bellman & C.-C. Lin), vol. 13, pp. 55–76. American Mathematical Society.CrossRefGoogle Scholar
Caflisch, R.E., Gargano, F., Sammartino, M. & Sciacca, V. 2022 Complex singularity analysis for vortex layer flows. J. Fluid Mech. 932, A21.CrossRefGoogle Scholar
Caflisch, R.E., Lombardo, M.C. & Sammartino, M.M.L. 2020 Vortex layers of small thickness. Commun. Pure Appl. Maths 73 (10), 2104–2179.CrossRefGoogle Scholar
Caflisch, R.E. & Orellana, O.F. 1986 Long time existence for a slightly perturbed vortex sheet. Commun. Pure Appl. Maths 39 (6), 807–838.CrossRefGoogle Scholar
Caflisch, R.E. & Orellana, O.F. 1989 Singular solutions and ill-posedness for the evolution of vortex sheets. SIAM J. Math. Anal. 20 (2), 293–307.CrossRefGoogle Scholar
Cowley, S., Baker, G.R. & Tanveer, S. 1999 On the formation of Moore curvature singularities in vortex sheets. J. Fluid Mech. 178, 233–267.CrossRefGoogle Scholar
Duchon, J. & Robert, R. 1988 Global vortex sheet solutions of Euler equations in the plane. J. Differ. Equ. 73 (2), 215–224.CrossRefGoogle Scholar
Ely, J. & Baker, G.R. 1994 High-precision calculations of vortex sheet motion. J. Comput. Phys. 111, 275–281.CrossRefGoogle Scholar
Helmholtz, P. 1868 XLIII. On discontinuous movements of fluids. Lond. Edinb. Dublin Philos. Mag. J. Sci. 36 (244), 337–346.CrossRefGoogle Scholar
Johnson, W.P. 2002 The curious history of Faà di Bruno's formula. Am. Math. Mon. 109 (3), 217–234.Google Scholar
Kaden, H. 1931 Aufwicklung einer unstabilen unstetigkeitsfläche. Ing.-Arch. 2 (2), 140–168.CrossRefGoogle Scholar
Krasny, R. 1986 a Desingularization of periodic vortex-sheet roll-up. J. Comput. Phys. 65, 65–93.CrossRefGoogle Scholar
Krasny, R. 1986 b A study of singularity formation in a vortex sheet by the point vortex approimation. J. Fluid Mech. 167, 292–313.CrossRefGoogle Scholar
Majda, A. & Bertozzi, A. 1992 Vorticity and Incompressible Flow. Cambridge University Press.Google Scholar
Meiron, D.I., Baker, G.R. & Orszag, S.A. 1982 Analytic structure of vortex sheet dynamics. Part 1. Kelvin–Helmholtz instability. J. Fluid Mech. 114, 283–298.CrossRefGoogle Scholar
Moore, D.W. 1978 The equation of motion of a vortex layer of small thickness. Stud. Appl. Maths 58, 119–140.CrossRefGoogle Scholar
Moore, D.W. 1979 The spontaneous appearance of a singularity in the shape of an evolving vortex sheet. Proc. R. Soc. Lond. A 365 (1720), 105–119.Google Scholar
Moore, D.W. & Saffman, P.G. 1973 Axial flow in laminar trailing vortices. Proc. R. Soc. Lond. A 333 (1595), 491–508.Google Scholar
Nitsche, M. 2001 Singularity formation in a cylindrical and a spherical vortex sheet. J. Comput. Phys. 173 (1), 208–230.CrossRefGoogle Scholar
Pullin, D.I. 1989 On similarity flows containing two-branched vortex sheets. In Mathematical aspects of vortex dynamics (ed. R.E. Caflisch), pp. 97–106. Society for Industrial and Applied Mathematics.Google Scholar
Pullin, D.I. & Phillips, W.R.C. 1981 On a generalization of Kaden's problem. J. Fluid Mech. 104, 45–53.CrossRefGoogle Scholar
Pullin, D.I. & Sader, J.E. 2021 On the starting vortex generated by a translating and rotating flat plate. J. Fluid Mech. 906, A9.CrossRefGoogle Scholar
Rosenhead, L. 1931 The formation of vortices from a surface of discontinuity. Proc. R. Soc. Lond. A 134 (823), 170–192.Google Scholar
Rott, N. 1956 Diffraction of a weak shock with vortex generation. J. Fluid Mech. 1 (1), 111–128.CrossRefGoogle Scholar
Shelley, M. 1992 A study of singularity formation in vortex sheet motion by a spectrally accurate vortex method. J. Fluid Mech. 244, 493–526.CrossRefGoogle Scholar
Sohn, S.-I. 2016 Self-similar roll-up of a vortex sheet driven by a shear flow: hyperbolic double spiral. Phys. Fluids 28 (6), 064104.CrossRefGoogle Scholar
Sulem, C., Sulem, P.-L., Bardos, C. & Frisch, U. 1981 Finite time analyticity for the two and three dimensional Kelvin–Helmholtz instability. Commun. Math. Phys. 80, 485–516.CrossRefGoogle Scholar
Thompson, W. 1871 Hydrokinetic solutions and observations. Phil. Mag. 4, 374.Google Scholar
Wu, S. 2006 Mathematical analysis of vortex sheets. Commun. Pure Appl. Maths 59, 1065–1206.CrossRefGoogle Scholar