Hostname: page-component-8448b6f56d-c4f8m Total loading time: 0 Render date: 2024-04-16T12:42:12.586Z Has data issue: false hasContentIssue false
  • English
  • Français

On velocity gradient dynamics and turbulent structure

Published online by Cambridge University Press:  02 September 2015

J. M. Lawson  and
J. R. Dawson
J. M. Lawson*
Affiliation:
Engineering Department, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
J. R. Dawson
Affiliation:
Department of Energy and Process Engineering, Norwegian University of Science and Technology, N-7491 Trondheim, Norway
*
†Email address for correspondence: jml70@cam.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

The statistics of the velocity gradient tensor 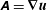$\unicode[STIX]{x1D63C}=\boldsymbol{{\rm\nabla}}\boldsymbol{u}$, which embody the fine scales of turbulence, are influenced by turbulent ‘structure’. Whilst velocity gradient statistics and dynamics have been well characterised, the connection between structure and dynamics has largely focused on rotation-dominated flow and relied upon data from numerical simulation alone. Using numerical and spatially resolved experimental datasets of homogeneous turbulence, the role of structure is examined for all local (incompressible) flow topologies characterisable by 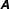$\unicode[STIX]{x1D63C}$. Structures are studied through the footprints they leave in conditional averages of the 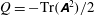$Q=-\text{Tr}(\unicode[STIX]{x1D63C}^{2})/2$ field, pertinent to non-local strain production, obtained using two complementary conditional averaging techniques. The first, stochastic estimation, approximates the 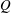$Q$ field conditioned upon 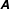$\unicode[STIX]{x1D63C}$ and educes quantitatively similar structure in both datasets, dissimilar to that of random Gaussian velocity fields. Moreover, it strongly resembles a promising model for velocity gradient dynamics recently proposed by Wilczek & Meneveau (J. Fluid Mech., vol. 756, 2014, pp. 191–225), but is derived under a less restrictive premise, with explicitly determined closure coefficients. The second technique examines true conditional averages of the 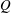$Q$ field, which is used to validate the stochastic estimation and provide insights towards the model’s refinement. Jointly, these approaches confirm that vortex tubes are the predominant feature of rotation-dominated regions and additionally show that shear layer structures are active in strain-dominated regions. In both cases, kinematic features of these structures explain alignment statistics of the pressure Hessian eigenvectors and why local and non-local strain production act in opposition to each other.

JFM classification

Turbulent Flows: Homogeneous turbulence Turbulent Flows: Turbulence modelling Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 780 , 10 October 2015 , pp. 60 - 98
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 1994 Stochastic estimation of conditional structure: a review. Appl. Sci. Res. 53 (3–4), 291–303.CrossRefGoogle Scholar
Alfonsi, G. 2006 Coherent structures of turbulence: methods of education and results. Appl. Mech. Rev. 59 (6), 307–323.CrossRefGoogle Scholar
Batchelor, G. K. 1951 Pressure fluctuations in isotropic turbulence. Math. Proc. Camb. Phil. Soc. 47, 359–374.Google Scholar
Bermejo-Moreno, I., Pullin, D. I. & Horiuti, K. 2009 Geometry of enstrophy and dissipation, grid resolution effects and proximity issues in turbulence. J. Fluid Mech. 620, 121–166.Google Scholar
Betchov, R. 1956 An inequality concerning the production of vorticity in isotropic turbulence. J. Fluid Mech. 1, 497–504.Google Scholar
Biferale, L. & Procaccia, I. 2005 Anisotropy in turbulent flows and in turbulent transport. Phys. Rep. 414 (23), 43–164.Google Scholar
Bodenschatz, E., Malinowski, S. P., Shaw, R. A. & Stratmann, F. 2010 Can we understand clouds without turbulence? Science 327 (5968), 970–971.Google Scholar
Bonnet, J.-P. & Delville, J. 2001 Review of coherent structures in turbulent free shear flows and their possible influence on computational methods. Flow Turbul. Combust. 66 (4), 333–353.Google Scholar
Cantwell, B. J. 1992 Exact solution of a restricted Euler equation for the velocity gradient tensor. Phys. Fluids A 4 (4), 782–793.Google Scholar
Cardesa, J. I., Mistry, D., Gan, L. & Dawson, J. R. 2013 Invariants of the reduced velocity gradient tensor in turbulent flows. J. Fluid Mech. 716, 597–615.Google Scholar
Chacin, J. M. & Cantwell, B. J. 2000 Dynamics of a low Reynolds number turbulent boundary layer. J. Fluid Mech. 404, 87–115.CrossRefGoogle Scholar
Chevillard, L., Lévêque, E., Taddia, F., Meneveau, C., Yu, H. & Rosales, C. 2011 Local and nonlocal pressure Hessian effects in real and synthetic fluid turbulence. Phys. Fluids 23 (9), 095108.CrossRefGoogle Scholar
Chevillard, L., Meneveau, C., Biferale, L. & Toschi, F. 2008 Modeling the pressure Hessian and viscous Laplacian in turbulence: comparisons with direct numerical simulation and implications on velocity gradient dynamics. Phys. Fluids 20 (10), 101504.Google Scholar
Chong, M. S., Perry, A. E. & Cantwell, B. J. 1990 A general classification of three-dimensional flow fields. Phys. Fluids A 2 (5), 765–777.Google Scholar
Chun, J., Koch, D. L., Rani, S. L., Ahluwalia, A. & Collins, L. R. 2005 Clustering of aerosol particles in isotropic turbulence. J. Fluid Mech. 536, 219–251.Google Scholar
Elsinga, G. E. & Marusic, I. 2010a Evolution and lifetimes of flow topology in a turbulent boundary layer. Phys. Fluids 22 (1), 015102.Google Scholar
Elsinga, G. E. & Marusic, I. 2010b Universal aspects of small-scale motions in turbulence. J. Fluid Mech. 662, 514–539.Google Scholar
Foucaut, J. M., Carlier, J. & Stanislas, M. 2004 PIV optimization for the study of turbulent flow using spectral analysis. Meas. Sci. Technol. 15 (6), 1046–1058.Google Scholar
Ganapathisubramani, B., Lakshminarasimhan, K. & Clemens, N. T. 2008 Investigation of three-dimensional structure of fine scales in a turbulent jet by using cinematographic stereoscopic particle image velocimetry. J. Fluid Mech. 598, 141–175.Google Scholar
Girimaji, S. S. & Pope, S. B. 1990 A diffusion model for velocity gradients in turbulence. Phys. Fluids A 2 (2), 242–256.Google Scholar
Hunt, J. C. R., Ishihara, T., Worth, N. A. & Kaneda, Y. 2014 Thin shear layer structures in high Reynolds number turbulence. Flow, Turbul. Combust. 92 (3), 607–649.CrossRefGoogle Scholar
Ishihara, T., Kaneda, Y., Yokokawa, M., Itakura, K. & Uno, A. 2007 Small-scale statistics in high-resolution direct numerical simulation of turbulence: Reynolds number dependence of one-point velocity gradient statistics. J. Fluid Mech. 592, 335–366.Google Scholar
Jiménez, J. & Wray, A. A. 1998 On the characteristics of vortex filaments in isotropic turbulence. J. Fluid Mech. 373, 255–285.CrossRefGoogle Scholar
Jiménez, J., Wray, A. A., Saffman, P. G. & Rogallo, R. S. 1993 The structure of intense vorticity in isotropic turbulence. J. Fluid Mech. 255, 65–90.Google Scholar
Kalelkar, C. 2006 Statistics of pressure fluctuations in decaying isotropic turbulence. Phys. Rev. E 73 (4), 046301.Google Scholar
Kerr, R. M. 1985 Higher-order derivative correlations and the alignment of small-scale structures in isotropic numerical turbulence. J. Fluid Mech. 153, 31–58.Google Scholar
Lawson, J. M. & Dawson, J. R. 2014 A scanning PIV method for fine-scale turbulence measurements. Exp. Fluids 55, 1857.Google Scholar
Leung, T., Swaminathan, N. & Davidson, P. A. 2012 Geometry and interaction of structures in homogeneous isotropic turbulence. J. Fluid Mech. 710, 453–481.Google Scholar
Li, Y., Perlman, E., Wan, M., Yang, Y., Meneveau, C., Burns, R., Chen, S., Szalay, A. & Eyink, G. 2008 A public turbulence database cluster and applications to study Lagrangian evolution of velocity increments in turbulence. J. Turbul. 9, 1–29.Google Scholar
Lüthi, B., Holzner, M. S. & Tsinober, A. 2009 Expanding the $Q$ – $R$ space to three dimensions. J. Fluid Mech. 641, 497–507.Google Scholar
Martin, J., Ooi, A., Chong, M. S. & Soria, J. 1998 Dynamics of the velocity gradient tensor invariants in isotropic turbulence. Phys. Fluids 10 (9), 2336–2346.Google Scholar
Meneveau, C. 2011 Lagrangian dynamics and models of the velocity gradient tensor in turbulent flows. Annu. Rev. Fluid Mech. 43 (1), 219–245.Google Scholar
Moisy, F. & Jiménez, J. 2004 Geometry and clustering of intense structures in isotropic turbulence. J. Fluid Mech. 513, 111–133.Google Scholar
Mui, R. C. Y., Dommermuth, D. G. & Novikov, E. A. 1996 Conditionally averaged vorticity field and turbulence modeling. Phys. Rev. E 53, 2355–2359.Google Scholar
Mullin, J. A. & Dahm, W. J. A. 2006 Dual-plane stereo particle image velocimetry measurements of velocity gradient tensor fields in turbulent shear flow. I: Accuracy assessments. Phys. Fluids 18 (3), 035101.Google Scholar
Nelkin, M. 1994 Universality and scaling in fully developed turbulence. Adv. Phys. 43 (2), 143–181.Google Scholar
Nie, Q. & Tanveer, S. 1999 A note on third order structure functions in turbulence. Proc. R. Soc. Lond. A 455 (1985), 1615–1635.Google Scholar
Nomura, K. K. & Post, G. K. 1998 The structure and dynamics of vorticity and rate of strain in incompressible homogeneous turbulence. J. Fluid Mech. 377, 65–97.Google Scholar
Ohkitani, K. 1993 Eigenvalue problems in three dimensional Euler flows. Phys. Fluids A 5 (10), 2570–2572.Google Scholar
Ohkitani, K. & Kishiba, S. 1995 Nonlocal nature of vortex stretching in an inviscid fluid. Phys. Fluids 7 (2), 411–421.Google Scholar
Ooi, A., Martin, J., Soria, J. & Chong, M. S. 1999 A study of the evolution and characteristics of the invariants of the velocity-gradient tensor in isotropic turbulence. J. Fluid Mech. 381, 141–174.Google Scholar
Pope, S. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Pumir, A. 1994 A numerical study of the mixing of a passive scalar in three dimensions in the presence of a mean gradient. Phys. Fluids 6 (6), 2118–2132.Google Scholar
Rabey, P. K., Wynn, A. & Buxton, O. R. H. 2015 The kinematics of the reduced velocity gradient tensor in a fully developed turbulent free shear flow. J. Fluid Mech. 767, 627–658.CrossRefGoogle Scholar
She, Z.-S., Jackson, E. & Orszag, S. A. 1991 Structure and dynamics of homogeneous turbulence: models and simulations. Proc. R. Soc. Lond. A 434 (1890), 101–124.Google Scholar
Siggia, E. D. 1981 Invariants for the one-point vorticity and strain rate correlation functions. Phys. Fluids 24 (11), 1934–1936.Google Scholar
Sreenivasan, K. R. 1995 On the universality of the Kolmogorov constant. Phys. Fluids 7 (11), 2778–2784.Google Scholar
Sreenivasan, K. R. 2004 Possible effects of small-scale intermittency in turbulent reacting flows. Flow, Turbul. Combust. 72 (2–4), 115–131.Google Scholar
Sreenivasan, K. R. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29 (1), 435–472.Google Scholar
Suman, S. & Girimaji, S. S. 2013 Velocity gradient dynamics in compressible turbulence: characterization of pressure-Hessian tensor. Phys. Fluids 25 (12), 125103.Google Scholar
Tokgoz, S., Elsinga, G. E., Delfos, R. & Westerweel, J. 2012 Spatial resolution and dissipation rate estimation in Taylor–Couette flow for tomographic PIV. Exp. Fluids 53 (3), 561–583.Google Scholar
Tsinober, A. 2009 An Informal Conceptual Introduction to Turbulence. Springer.Google Scholar
Vincent, A. & Meneguzzi, M. 1991 Spatial structure and statistical properties of homogeneous turbulence. J. Fluid Mech. 225, 1–20.Google Scholar
Vincent, A. & Meneguzzi, M. 1994 Dynamics of vorticity tubes in homogeneous turbulence. J. Fluid Mech. 258, 245–254.CrossRefGoogle Scholar
Wallace, J. M. 2009 Twenty years of experimental and direct numerical simulation access to the velocity gradient tensor: What have we learned about turbulence? Phys. Fluids 21 (2), 021301.Google Scholar
Wilczek, M. & Meneveau, C. 2014 Pressure Hessian and viscous contributions to velocity gradient statistics based on Gaussian random fields. J. Fluid Mech. 756, 191–225.Google Scholar
Worth, N. A. & Nickels, T. B. 2011 Time-resolved volumetric measurement of fine-scale coherent structures in turbulence. Phys. Rev. E 84 (2), 025301.Google Scholar
Zheng, Q. S. 1993 On the representations for isotropic vector-valued, symmetric tensor-valued and skew-symmetric tensor-valued functions. Intl J. Engng Sci. 31 (7), 1013–1024.Google Scholar