Article contents
On velocity and reactive scalar spectra in turbulent premixed flames
Published online by Cambridge University Press: 07 August 2014
Abstract
Kinetic energy and reactive scalar spectra in turbulent premixed flames are studied from compressible three-dimensional direct numerical simulations (DNS) of a temporally evolving rectangular slot-jet premixed flame, a statistically one-dimensional configuration. The flames correspond to a lean premixed hydrogen–air mixture at an equivalence ratio of 0.7, preheated to 700 K and at 1 atm, and three DNS are considered with a fixed jet Reynolds number of 10 000 and a jet Damköhler number varying between 0.13 and 0.54. For the study of spectra, motivated by the need to account for density change, which can be locally strong in premixed flames, a new density-weighted definition for two-point velocity/scalar correlations is proposed. The density-weighted two-point correlation tensor retains the essential properties of its constant-density (incompressible) counterpart and recovers the density-weighted Reynolds stress tensor in the limit of zero separation. The density weighting also allows the derivation of balance equations for velocity and scalar spectrum functions in the wavenumber space that illuminate physics unique to combusting flows. Pressure–dilatation correlation is a source of kinetic energy at high wavenumbers and, analogously, reaction rate–scalar fluctuation correlation is a high-wavenumber source of scalar energy. These results are verified by the spectra constructed from the DNS data. The kinetic energy spectra show a distinct inertial range with a 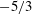 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}-5/3$ scaling followed by a ‘diffusive–reactive’ range at higher wavenumbers. The exponential drop-off in this range shows a distinct inflection in the vicinity of the wavenumber corresponding to a laminar flame thickness,
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}-5/3$ scaling followed by a ‘diffusive–reactive’ range at higher wavenumbers. The exponential drop-off in this range shows a distinct inflection in the vicinity of the wavenumber corresponding to a laminar flame thickness, 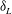 $\delta _L$, and this is attributed to the contribution from the pressure–dilatation term in the energy balance in wavenumber space. Likewise, a clear spike in spectra of major reactant species (hydrogen) arising from the reaction-rate term is observed at wavenumbers close to
$\delta _L$, and this is attributed to the contribution from the pressure–dilatation term in the energy balance in wavenumber space. Likewise, a clear spike in spectra of major reactant species (hydrogen) arising from the reaction-rate term is observed at wavenumbers close to 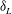 $\delta _L$. It appears that in the inertial range classical scaling laws for the spectra involving the Kolmogorov scale are applicable, but in the high-wavenumber range where chemical reactions have a strong signature the laminar flame thickness produces a better collapse. It is suggested that a full scaling should perhaps involve the Kolmogorov scale, laminar flame thickness, Damköhler number and Karlovitz number.
$\delta _L$. It appears that in the inertial range classical scaling laws for the spectra involving the Kolmogorov scale are applicable, but in the high-wavenumber range where chemical reactions have a strong signature the laminar flame thickness produces a better collapse. It is suggested that a full scaling should perhaps involve the Kolmogorov scale, laminar flame thickness, Damköhler number and Karlovitz number.
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 59
- Cited by




