Hostname: page-component-76fb5796d-skm99 Total loading time: 0 Render date: 2024-04-25T14:31:59.563Z Has data issue: false hasContentIssue false
  • English
  • Français

On the relevance of Reynolds stresses in resolvent analyses of turbulent wall-bounded flows

Published online by Cambridge University Press:  02 April 2019

Pierluigi Morra Open the ORCID record for Pierluigi Morra [Opens in a new window] ,
Onofrio Semeraro Open the ORCID record for Onofrio Semeraro [Opens in a new window] ,
Dan S. Henningson Open the ORCID record for Dan S. Henningson [Opens in a new window]  and
Carlo Cossu Open the ORCID record for Carlo Cossu [Opens in a new window]
Pierluigi Morra
Affiliation:
KTH Royal Institute of Technology, Linné FLOW Centre, SE-10044, Stockholm, Sweden
Onofrio Semeraro
Affiliation:
LIMSI, UPR 3251 CNRS/Université Paris-Saclay, 91400 Orsay, France
Dan S. Henningson
Affiliation:
KTH Royal Institute of Technology, Linné FLOW Centre, SE-10044, Stockholm, Sweden
Carlo Cossu*
Affiliation:
LHEEA, UMR 6598 CNRS/Centrale Nantes, 44300 Nantes, France
*
†Email address for correspondence: carlo.cossu@ec-nantes.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

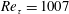The ability of linear stochastic response analysis to estimate coherent motions is investigated in turbulent channel flow at the friction Reynolds number $\text{Re}_{\unicode[STIX]{x1D70F}}=1007$. The analysis is performed for spatial scales characteristic of buffer-layer and large-scale motions by separating the contributions of different temporal frequencies. Good agreement between the measured spatio-temporal power spectral densities and those estimated by means of the resolvent is found when the effect of turbulent Reynolds stresses, modelled with an eddy-viscosity associated with the turbulent mean flow, is included in the resolvent operator. The agreement is further improved when the flat forcing power spectrum (white noise) is replaced with a power spectrum matching the measures. Such a good agreement is not observed when the eddy-viscosity terms are not included in the resolvent operator. In this case, the estimation based on the resolvent is unable to select the right peak frequency and wall-normal location of buffer-layer motions. Similar results are found when comparing truncated expansions of measured streamwise velocity power spectral densities based on a spectral proper orthogonal decomposition to those obtained with optimal resolvent modes.

JFM classification

Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 867 , 25 May 2019 , pp. 969 - 984
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

del Álamo, J. C. & Jiménez, J. 2006 Linear energy amplification in turbulent channels. J. Fluid Mech. 559, 205–213.Google Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.Google Scholar
Bendat, J. S. & Piersol, A. G. 1986 Random Data: Analysis and Measurement Procedures. Wiley.Google Scholar
Böberg, L. & Brosa, U. 1988 Onset of turbulence in a pipe. Z. Naturforsch. A 43a, 697–726.Google Scholar
Bottaro, A., Souied, H. & Galletti, B. 2006 Formation of secondary vortices in a turbulent square-duct flow. AIAA J. 44, 803–811.Google Scholar
Butler, K. M. & Farrell, B. F. 1992 Three-dimensional optimal perturbations in viscous shear flow. Phys. Fluids A 4, 1637–1650.Google Scholar
Butler, K. M. & Farrell, B. F. 1993 Optimal perturbations and streak spacing in wall-bounded turbulent shear flow. Phys. Fluids 5, 774–777.Google Scholar
Cess, R. D.1958 A survey of the literature on heat transfer in turbulent tube flow. Res. Rep. 8–0529–R24. Westinghouse.Google Scholar
Chevalier, M., Schlatter, P., Lundbladh, A. & Henningson, D. S.2007 A pseudo-spectral solver for incompressible boundary layer flows. Tech. Rep. TRITA-MEK 2007:07. Royal Institute of Technology (KTH), Dept. of Mechanics, Stockholm.Google Scholar
Corrsin, S. & Kistler, A. L. 1954 The free-stream boundaries of turbulent flows. Tech. Note 3133, 120–130, NACA.Google Scholar
Cossu, C. & Hwang, Y. 2017 Self-sustaining processes at all scales in wall-bounded turbulent shear flows. Phil. Trans. R. Soc. Lond. A 375 (2089), 20160088.Google Scholar
Cossu, C., Pujals, G. & Depardon, S. 2009 Optimal transient growth and very large scale structures in turbulent boundary layers. J. Fluid Mech. 619, 79–94.Google Scholar
Ellingsen, T. & Palm, E. 1975 Stability of linear flow. Phys. Fluids 18, 487–488.Google Scholar
Farrell, B. F. & Ioannou, P. J. 1993a Optimal excitation of three-dimensional perturbations in viscous constant shear flow. Phys. Fluids 5, 1390–1400.Google Scholar
Farrell, B. F. & Ioannou, P. J. 1993b Stochastic forcing of the linearized Navier–Stokes equation. Phys. Fluids A 5, 2600–2609.Google Scholar
Gustavsson, L. H. 1991 Energy growth of three-dimensional disturbances in plane Poiseuille flow. J. Fluid Mech. 224, 241–260.Google Scholar
Hamilton, J. M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.Google Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Hwang, Y. & Cossu, C. 2010a Amplification of coherent streaks in the turbulent Couette flow: an input-output analysis at low Reynolds number. J. Fluid Mech. 643, 333–348.Google Scholar
Hwang, Y. & Cossu, C. 2010b Linear non-normal energy amplification of harmonic and stochastic forcing in turbulent channel flow. J. Fluid Mech. 664, 51–73.Google Scholar
Hwang, Y. & Cossu, C. 2010c Self-sustained process at large scales in turbulent channel flow. Phys. Rev. Lett. 105 (4), 044505.Google Scholar
Hwang, Y. & Cossu, C. 2011 Self-sustained processes in the logarithmic layer of turbulent channel flows. Phys. Fluids 23, 061702.Google Scholar
Illingworth, S. J., Monty, J. P. & Marusic, I. 2018 Estimating large-scale structures in wall turbulence using linear models. J. Fluid Mech. 842, 146–162.Google Scholar
Kim, K. C. & Adrian, R. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.Google Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30, 741–773.Google Scholar
Komminaho, J., Lundbladh, A. & Johansson, A. V. 1996 Very large structures in plane turbulent Couette flow. J. Fluid Mech. 320, 259–285.Google Scholar
Kovasznay, L. S. G., Kibens, V. & Blackwelder, R. F. 1970 Large-scale motion in the intermittent region of a turbulent boundary layer. J. Fluid Mech. 41, 283–325.Google Scholar
Landahl, M. T. 1980 A note on an algebraic instability of inviscid parallel shear flows. J. Fluid Mech. 98, 243–251.Google Scholar
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to Re 𝜏 ≈ 5200. J. Fluid Mech. 774, 395–415.Google Scholar
Lumley, JL 1970 Stochastic Tools in Turbulence. Academic Press.Google Scholar
Malkus, W. V. R. 1956 Outline of a theory of turbulent shear flow. J. Fluid Mech. 1, 521–539.Google Scholar
McKeon, B. J. 2017 The engine behind (wall) turbulence: Perspectives on scale interactions. J. Fluid Mech. 817, P1.Google Scholar
McKeon, B. J. & Sharma, A. S. 2010 A critical-layer framework for turbulent pipe flow. J. Fluid Mech. 658, 336–382.Google Scholar
Moffatt, H. K. 1967 The interaction of turbulence with strong wind shear. In Proceedings of the URSI-IUGG Colloquium on Atmospheric Turbulence and Radio Wave Propagation (ed. Yaglom, A. M. & Tatarsky, V. I.), pp. 139–154. Nauka.Google Scholar
Picard, C. & Delville, J. 2000 Pressure velocity coupling in a subsonic round jet. Intl J. Heat Fluid Flow 21 (3), 359–364.Google Scholar
Pujals, G., García-Villalba, M., Cossu, C. & Depardon, S. 2009 A note on optimal transient growth in turbulent channel flows. Phys. Fluids 21, 015109.Google Scholar
Reddy, S. C. & Henningson, D. S. 1993 Energy growth in viscous channel flows. J. Fluid Mech. 252, 209–238.Google Scholar
Reddy, S. C., Schmid, P. J., Baggett, J. S. & Henningson, D. S. 1998 On the stability of streamwise streaks and transition thresholds in plane channel flows. J. Fluid Mech. 365, 269–303.Google Scholar
Reynolds, W. C. & Hussain, A. K. M. F. 1972 The mechanics of an organized wave in turbulent shear flow. Part 3. Theoretical models and comparisons with experiments. J. Fluid Mech. 54 (02), 263–288.Google Scholar
Reynolds, W. C. & Tiederman, W. G. 1967 Stability of turbulent channel flow, with application to Malkus’s theory. J. Fluid Mech. 27 (02), 253–272.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.Google Scholar
Schmidt, O. T., Towne, A., Rigas, G., Colonius, T. & Brès, G. A. 2018 Spectral analysis of jet turbulence. J. Fluid Mech. 855, 953–982.Google Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.Google Scholar
Semeraro, O., Jaunet, V., Jordan, P., Cavalieri, A. V. & Lesshafft, L. 2016 Stochastic and harmonic optimal forcing in subsonic jets. In 22nd AIAA/CEAS Aeroacoustics Conference, p. 2935. AIAA.Google Scholar
Towne, A., Schmidt, O. T. & Colonius, T. 2018 Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis. J. Fluid Mech. 847, 821–867.Google Scholar
Trefethen, L. N., Trefethen, A. E., Reddy, S. C. & Driscoll, T. A. 1993 A new direction in hydrodynamic stability: beyond eigenvalues. Science 261, 578–584.Google Scholar
Waleffe, F. 1995 Hydrodynamic stability and turbulence: beyond transients to a self-sustaining process. Stud. Appl. Maths 95, 319–343.Google Scholar
Zare, A., Jovanović, M. R. & Georgiou, T. T. 2017 Colour of turbulence. J. Fluid Mech. 812, 636–680.Google Scholar