Article contents
On the problem of large-scale magnetic field generation in rotating compressible convection
Published online by Cambridge University Press: 16 April 2013
Abstract
Mean-field dynamo theory suggests that turbulent convection in a rotating layer of electrically conducting fluid produces a significant  $\alpha $-effect, which is one of the key ingredients in any mean-field dynamo model. Provided that this
$\alpha $-effect, which is one of the key ingredients in any mean-field dynamo model. Provided that this  $\alpha $-effect operates more efficiently than (turbulent) magnetic diffusion, such a system should be capable of sustaining a large-scale dynamo. However, in the Boussinesq model that was considered by Cattaneo & Hughes (J. Fluid Mech., vol. 553, 2006, pp. 401–418) the dynamo produced small-scale, intermittent magnetic fields with no significant large-scale component. In this paper, we consider the compressible analogue of the rotating convective layer that was considered by Cattaneo & Hughes (2006). Varying the horizontal scale of the computational domain, we investigate the dependence of the dynamo upon the rotation rate. Our simulations indicate that these turbulent compressible flows can drive a small-scale dynamo but, even when the layer is rotating very rapidly (with a mid-layer Taylor number of
$\alpha $-effect operates more efficiently than (turbulent) magnetic diffusion, such a system should be capable of sustaining a large-scale dynamo. However, in the Boussinesq model that was considered by Cattaneo & Hughes (J. Fluid Mech., vol. 553, 2006, pp. 401–418) the dynamo produced small-scale, intermittent magnetic fields with no significant large-scale component. In this paper, we consider the compressible analogue of the rotating convective layer that was considered by Cattaneo & Hughes (2006). Varying the horizontal scale of the computational domain, we investigate the dependence of the dynamo upon the rotation rate. Our simulations indicate that these turbulent compressible flows can drive a small-scale dynamo but, even when the layer is rotating very rapidly (with a mid-layer Taylor number of 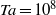 $Ta= 1{0}^{8} $), we find no evidence for the generation of a significant large-scale component of the magnetic field on a dynamical time scale. Like Cattaneo & Hughes (2006), we measure a negligible (time-averaged)
$Ta= 1{0}^{8} $), we find no evidence for the generation of a significant large-scale component of the magnetic field on a dynamical time scale. Like Cattaneo & Hughes (2006), we measure a negligible (time-averaged)  $\alpha $-effect when a uniform horizontal magnetic field is imposed across the computational domain. Although the total horizontal magnetic flux is a conserved quantity in these simulations, the (depth-dependent) horizontally averaged magnetic field always exhibits strong fluctuations. If these fluctuations are artificially suppressed within the code, we measure a significant mean electromotive force that is comparable to that found in related calculations in which the
$\alpha $-effect when a uniform horizontal magnetic field is imposed across the computational domain. Although the total horizontal magnetic flux is a conserved quantity in these simulations, the (depth-dependent) horizontally averaged magnetic field always exhibits strong fluctuations. If these fluctuations are artificially suppressed within the code, we measure a significant mean electromotive force that is comparable to that found in related calculations in which the  $\alpha $-effect is measured using the test-field method, even though we observe no large-scale dynamo action.
$\alpha $-effect is measured using the test-field method, even though we observe no large-scale dynamo action.
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 22
- Cited by




